为了降低多路径效应对导航定位精度的影响,许多学者从硬件改进和数据处理算法两个方面开展抑制多路径误差的研究。采用抑制多路径的天线会增加设备的重量和成本,常用于跟踪站等固定观测,能够提高定位精度,但不便于携带,难以适应大众行人导航的需求。针对数据处理算法方面的改进措施,主要有信噪比法[1]和基于多路径周日重复性的方法[2-3]等。信噪比法就是通过降低低信噪比观测值的权重来抑制多路径对定位结果的影响,但在城市环境下,信噪比下降的原因更为复杂,单一的信噪比法难以有效解决多路径问题。多路径周日重复性方法主要利用多路径误差周日重复的特性,通过各种滤波算法,从观测值或定位结果中分离出多路径误差的影响[4]。在环境变化很小的静态观测条件下,这种方法非常有效,但对于具有动态、环境变换快等特点的行人导航用户来说,该方法并不适用。纯反射信号(NLOS)误差的大小与环境关系密切,有学者提出基于外源信息如周围建筑物高程或3D地图[5-10]来识别并消除NLOS效应,该方法难以推广到行人导航上。
大众用户的运动环境变化大,多路径和NLOS难以准确建模,当前的研究方法无法应用于行人导航。行人导航一般采用手机内置接收机模块和低成本导航模块,因此多路径和NLOS会对定位结果造成很大的影响。用户端集成了GPS、GLONASS和BDS多系统接收机,可以观测到的卫星数量多,识别并剔除多路径效应和NLOS效应造成的粗差能够有效提高导航精度。多路径与NLOS对不同接收机、不同测量值的影响不同,因此研究和分析低成本导航型接收机的多路径和NLOS误差特性至关重要。
本文从多路径和NLOS产生的原因出发,采用双差模型来提取不同观测值中的多路径误差,然后分析和评估了典型城市环境下多路径信号和纯反射(NLOS)对多普勒、伪距和载波相位观测值的影响,进而总结不同环境下多路径误差和NLOS误差的特性,为多路径和NLOS引起的粗差数据剔除提供依据。
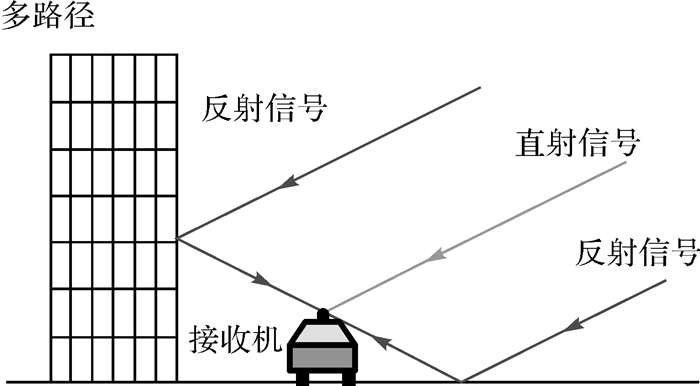
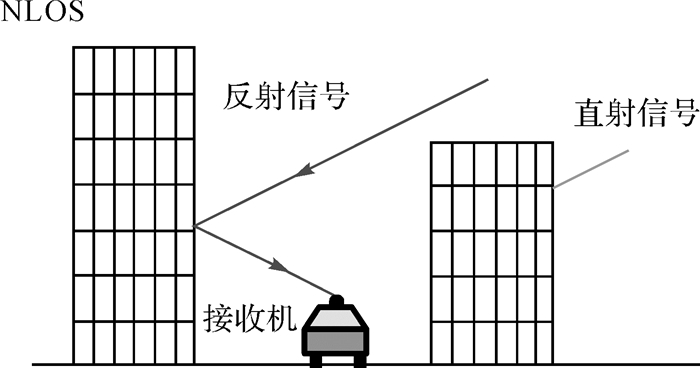
1 多路径与NLOS在典型的城市场景下,接收机在接收干净的直射信号(LOS)的同时,也会接收到多路径信号和纯反射信号。这两者形成原因不同,分析与处理方法也有差异。接收机内部复制C/A码,然后将此复制码与其接收到的GNSS信号作相关运算,最后根据所得的C/A码自相关函数的峰值来测量码相位。如果接收到的GNSS信号是由直射波和多个反射波叠加而成的,如图 1所示,那么接收机内部复制的C/A码会同时与直射波和各个反射波作相关运算,使原本只反映直射波码相位情况的三角形自相关函数的主峰遭到变形、破坏,从而降低了码相位及伪距的测量精度[11]。码跟踪误差可以达到半个码片,其大小取决于接收机内部构造、直射波与反射波的信号强度,以及路径延迟和相位差。载波跟踪误差限制在1/4个波长以内,而且变化的叠加波很可能造成卫星载波信号的失锁。当直射信号被遮住,接收机只收到反射信号,如图 2所示,这就是纯反射信号。NLOS造成的伪距和载波测量误差等于增加的路径延迟,即卫星到接收机间反射波与直射波传播路径的差值。纯反射信号强度可能很弱也可能较强,造成的误差为正值,数值大小没有限制[5-7]。
多普勒频移fd是发射频率与接收频率之间的差异。若卫星相应的发射信号波长为λs,则接收机接收到的卫星信号的多普勒频移为
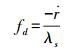 (1)
(1) 式中,
复杂城市环境的主要元素是树木和高楼。树叶使卫星信号衰减,地面反射的信号与衰减后的直射信号叠加容易发生多路径效应。两边高楼的街道容易造成卫星信号的反射与遮挡。一般的居民楼在十几米,商业圈中商场等高楼可能有几十米甚至更高,这种环境下的可见天空狭长,容易发生NLOS,且反射路径要比直射路径长很多,因此造成的误差很大。
2 多路径和NLOS误差提取方法GNSS单频伪距与载波相位测量模型为
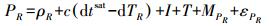 (2)
(2) 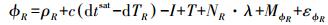 (3)
(3) 式中,PR为伪距观测值;ρR为卫星到接收机的几何距离;c为光速;dtsat为卫星钟差;dTR为接收机钟差;I为电离层延迟;T为对流层延迟;MPR和MϕR分别为伪距多径误差和载波多径误差;εP和εϕ分别为伪距和载波的测量噪声;N为模糊度;λ为波长。
对两个测站观测到的同一颗GNSS卫星的伪距和载波相位观测值作差可得到站间单差观测值,消除了卫星钟差的影响,对于短基线的情况,也可消除大气延迟误差和卫星位置误差的影响。A、B分别表示基站和流动站,Δ为单差算子,经过站间单差后
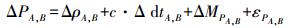 (4)
(4) 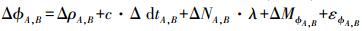 (5)
(5) 站间单差后,同一时刻对两颗不同卫星的单差观测值再次求差可得到站星双差观测值,能进一步消除接收机钟差的影响。在本文站星双差时,选择载噪比高和卫星高度角较大的作为基准星,避免基准星受多路径或NLOS误差的影响。站星双差观测方程为
 (6)
(6) 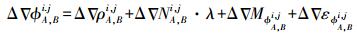 (7)
(7) 式中,Δ∇为双差算子;i、j为不同卫星。
选取观测条件良好的已知点上架设GNSS接收机作为基站,选取树木遮挡或高楼附近的测站作为流动站,通过RTK或全站仪导线的方法测定其准确坐标。将两台接收机的精确坐标和卫星位置代入式(6)和式(7),最终得到
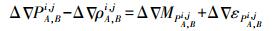 (8)
(8)  (9)
(9) 伪距双差残差中包含伪距多路径或NLOS误差和双差伪距噪声,载波双差残差中包含双差模糊度、载波多路径或NLOS误差和双差载波噪声。利用伪距初始化载波的模糊度,可以固定大部分的模糊度,缩小残留的载波模糊度值。
3 试验数据分析与验证 3.1 试验场地与设备为分析干涉多路径和NLOS误差特性,本文试验的基站和流动站都使用低成UBLOX-NEO-M8T多系统单频GNSS接收机,分别在高楼旁和林荫树下静态采集数据,试验场景如图 3和图 4所示。图 3为商场外高楼,数据采集点A两侧是几十米的高楼,可见天空狭长,易产生NLOS效应;图 4为校园林荫道,数据采集点B在行人道旁茂密的树下,树叶遮挡明显。基准观测站的天线设置在15层高的教学楼楼顶,观测条件良好,而且基站的天线带有抑制多路径的choke-ring天线。本次试验采集GPS+BDS原始数据,观测时长3~4 h,采样间隔1 s,重点分析GPS+BDS卫星信号的多路径和NLOS误差。

|
| 图 3 商场高楼 |

|
| 图 4 校园林荫道 |
为了实现既能紧密跟踪信号输出精确的载波相位测量值,又能更好地解决用户高动态运动造成的多普勒频率及频率变化率较大的问题,NEO-M8T采用锁频环和锁相环交替的载波环。锁相环的噪声宽带较窄,跟踪能力强,输出的载波相位测量值相当准确,但噪声较强、多普勒频率变化大时信号锁定困难;锁频环噪声宽带宽,动态性能好,可以跟踪信噪比更低的信号,但测量噪声较高[11, 16]。
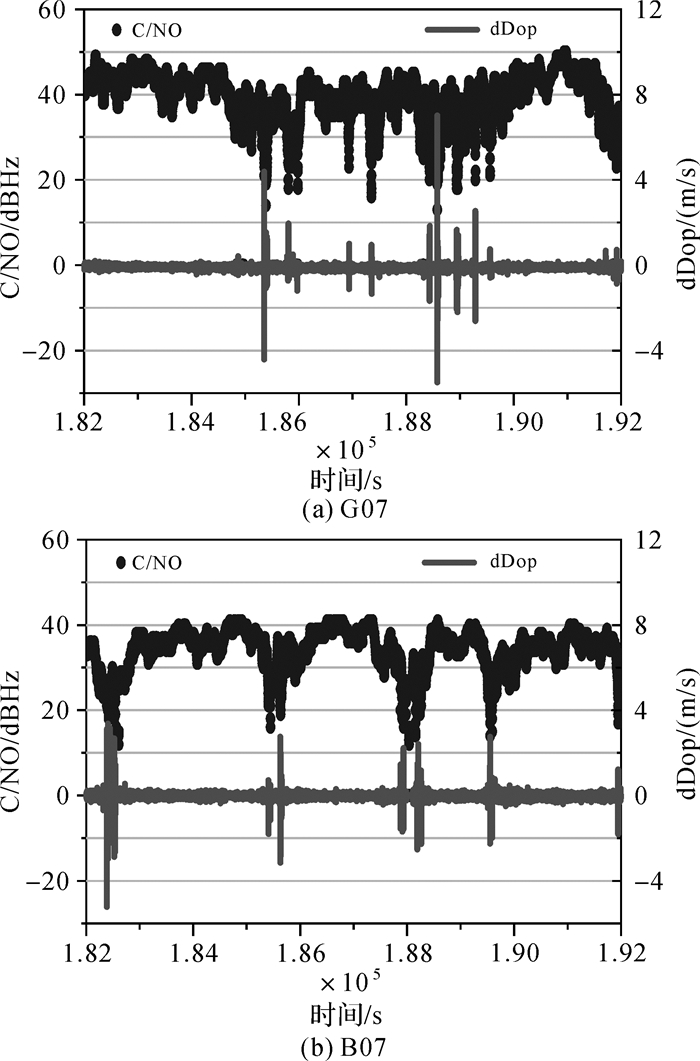
3.2 载噪比C/N0与多普勒误差对于静态测量,多普勒测量值理论上受多路径和NLOS的影响较小,除非反射面是移动物体[8]。图 5(a)和(b)分别为位于校园林荫道上流动站G07和B07卫星的多普勒历元差dDop与载噪比C/N0,可以看出当C/N0下降时多普勒历元差波动明显增大。图 6(a)和(b)分别为高楼下流动站G03和B07卫星的多普勒历元差dDop与载噪比C/N0,当载噪比下降时,多普勒历元差同样会出现明显的波动。
|
| 图 5 校园林荫道上流动站多普勒历元差与C/N0 |

|
| 图 6 商场外高楼下多普勒历元差与C/N0 |
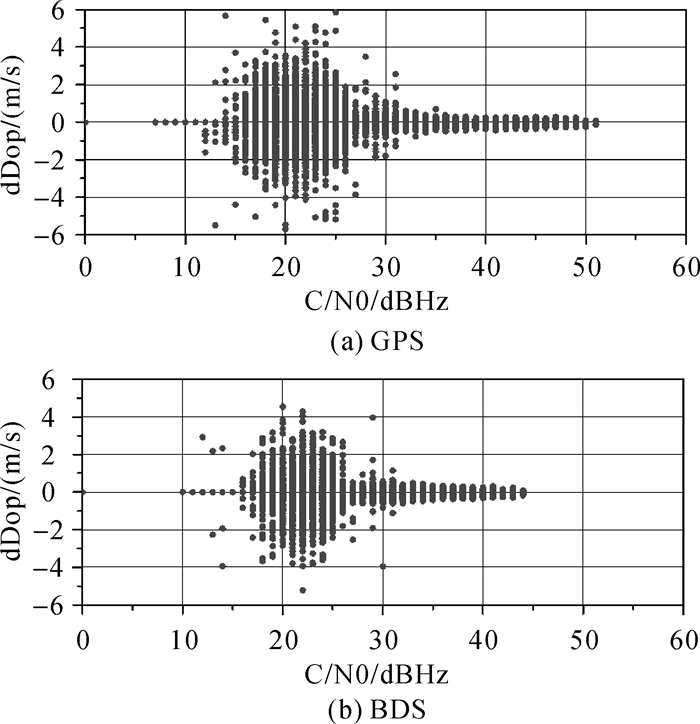
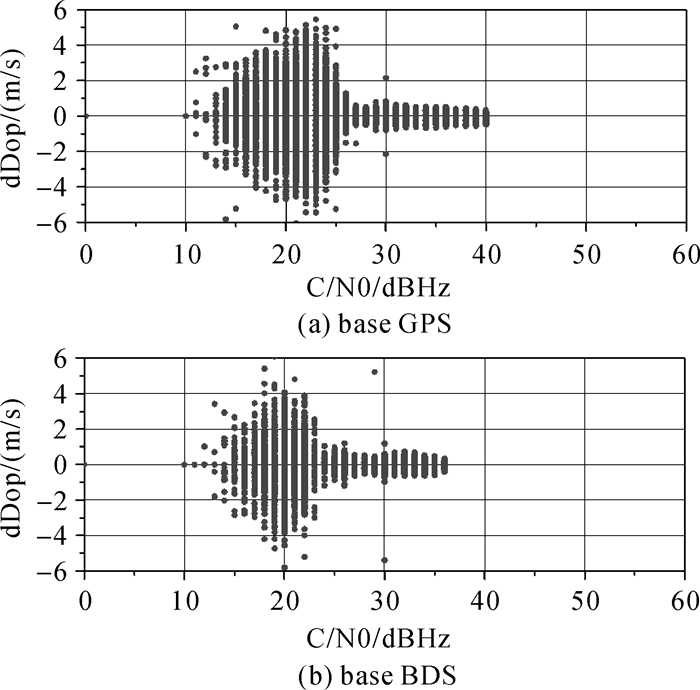
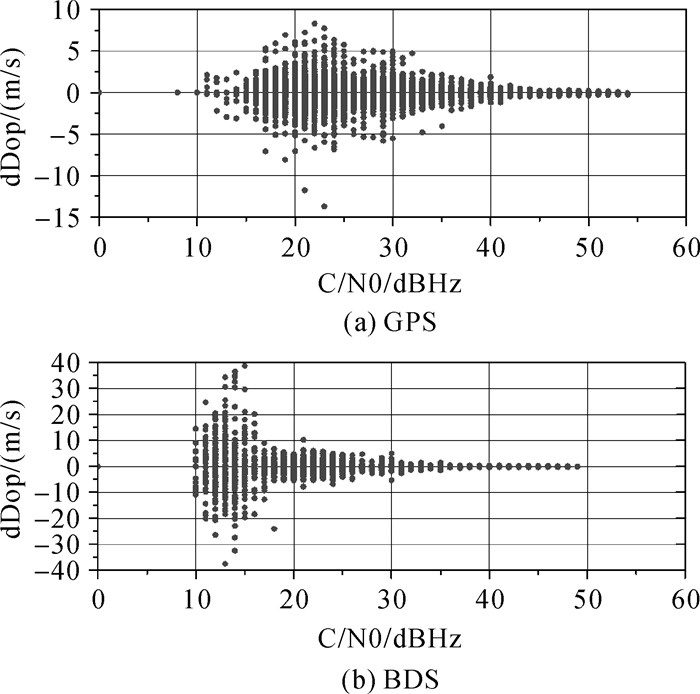
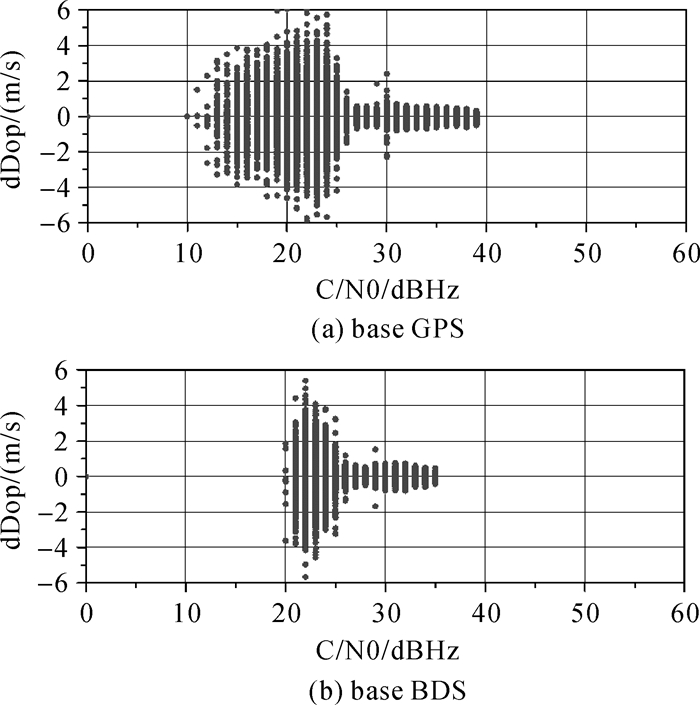
将两个流动站和基站整个观测时段内所有GPS卫星的观测数据均以C/N0为横坐标,或除去GEO卫星的BDS卫星的C/N0为横坐标,以多普勒历元差为纵坐标,分别绘制图 7-图 10。其中图 7为校园林荫道下的观测数据,图 8为同时段基站在观测条件良好环境下的观测数据,图 9为商场大楼旁的观测数据,图 10为同时段基站在观测条件良好环境下的观测数据。由于基站的天线设在楼顶,需要连接较长的馈线,使接收到的卫星信号强度衰减,因此基站C/N0的最大值要比流动站小。可以看出,C/N0较小时多普勒观测值噪声较大,C/N0较大时多普勒噪声较小。在观测条件较好的情况下,C/N0小于27 dBHz时,多普勒噪声明显增加,绝对值从1 m/s以内增加到6 m/s以内,北斗和GPS卫星影响相同。在校园林荫道上C/N0小于30 dBHz时,多普勒噪声明显增加,绝对值从1 m/s以内增加到6 m/s以内,北斗和GPS卫星影响相同。商场外高楼下,C/N0在30~40 dBHz时多普勒噪声仍高于正常值,GPS卫星的多普勒噪声绝对值增大到十几米每秒,北斗的多普勒噪声绝对值增大到几十米每秒。由于M8T导航型接收机采用窄带锁相环和宽带锁频环交替的模式,商场外两边有高楼遮挡,容易发生NLOS,不同的反射点使得NRID变化较快,并且由于反射面的形状和表面光滑程度不同造成NLOS信号持续的出现与消失,接收机捕获到信号需要较大的噪声带宽。C/N0与噪声带宽无关,在C/N0相同时,接收机在商场外的高楼下需要更大的带宽,多普勒噪声较大;接收机在校园林荫道的树下虽然容易发生多路径效应,但信号容易捕获与跟踪,带宽逐渐减小,多普勒噪声较小。
|
| 图 7 校园林荫道GPS、BDS的C/N0与多普勒 |
|
| 图 8 同时段基站GPS、BDS的C/N0与多普勒 |
|
| 图 9 商场外GPS、BDS的C/N0与多普勒 |
|
| 图 10 同时段基站GPS、BDS的C/N0与多普勒 |
通过静态实测数据,利用双差方法提取多路径或NLOS误差,分析不同环境下多路径和NLOS对伪距观测值、载波观测值和原始多普勒观测值的影响。
3.3.1 林荫道试验对林荫道上流动站数据与基站组合,分别提取伪距和载波相位的多路径或NLOS延迟误差。根据多路径信号的理论分析,判断伪距双差残差较大、载波相位双差残差没有明显变化的卫星为受到多路径影响的卫星。从本次试验中取一颗发生多路径效应的GPS卫星(PRN为11)和一颗发生多路径效应的BDS卫星(PRN为10)分别绘制成图 11和图 12。

|
| 图 11 校园林荫道G11的载噪比、伪距双差残差、载波相位双差残差和多普勒历元差 |
|
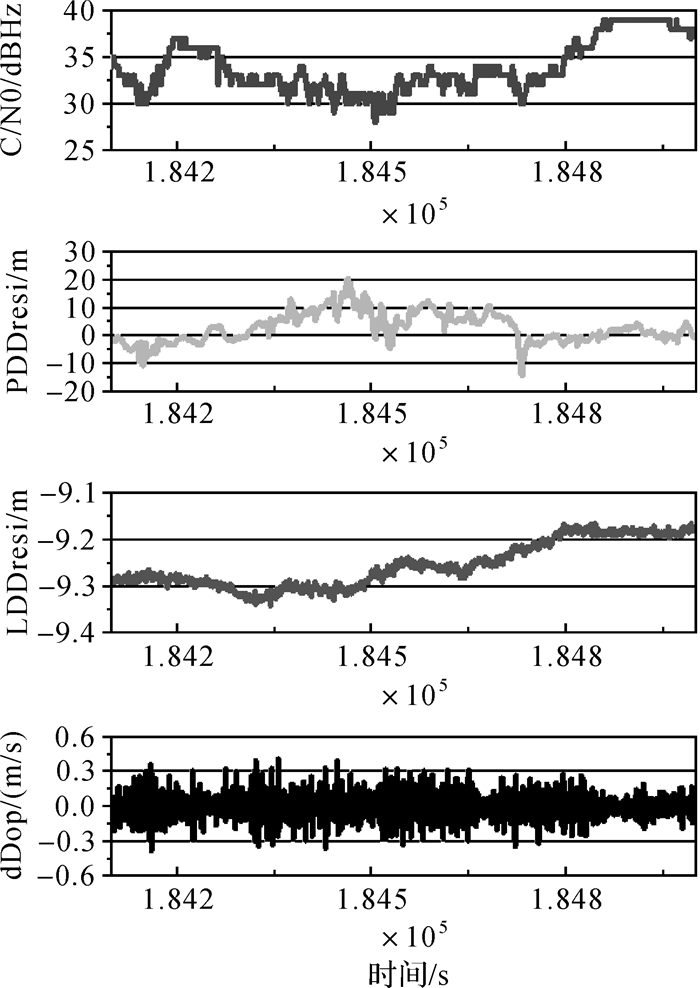
| 图 12 校园林荫道B10的载噪比、伪距双差残差、载波相位双差残差和多普勒历元差 |
可以看出,当GPS卫星的C/N0低于30 dBHz时,伪距残差存在几十米的波动,载波相位残差仍然保持连续(其中包含残余双差模糊度),整个弧段变化在1~2 dm,多普勒历元差大多在±0.3 m以内,随着C/N0的增加而逐渐减少。BDS卫星也出现类似的情况,但是BDS的C/N0在35 dBHz以下时,伪距残差就会出现10~20 m的波动,其卫星也有类似情况。对伪距观测值产生多达几十米的延迟误差,对载波相位观测值看不出明显变化,与多路径信号的理论分析一致,说明在林荫道上,卫星信号穿过树叶和树木,容易产生多路径信号干扰。
3.3.2 高楼附近试验与林荫道试验类似,根据NLOS信号的理论分析,判断伪距和载波双差残差较大且影响相同的卫星为受到NLOS影响的卫星。从本次试验中取一颗发生NLOS效应的GPS卫星(PRN为17)和一颗发生NLOS效应的BDS卫星(PRN为7)分别绘制成图 13和图 14。

|
| 图 13 商场建筑物旁G17的载噪比、伪距双差残差、载波相位双差残差和多普勒历元差 |
|
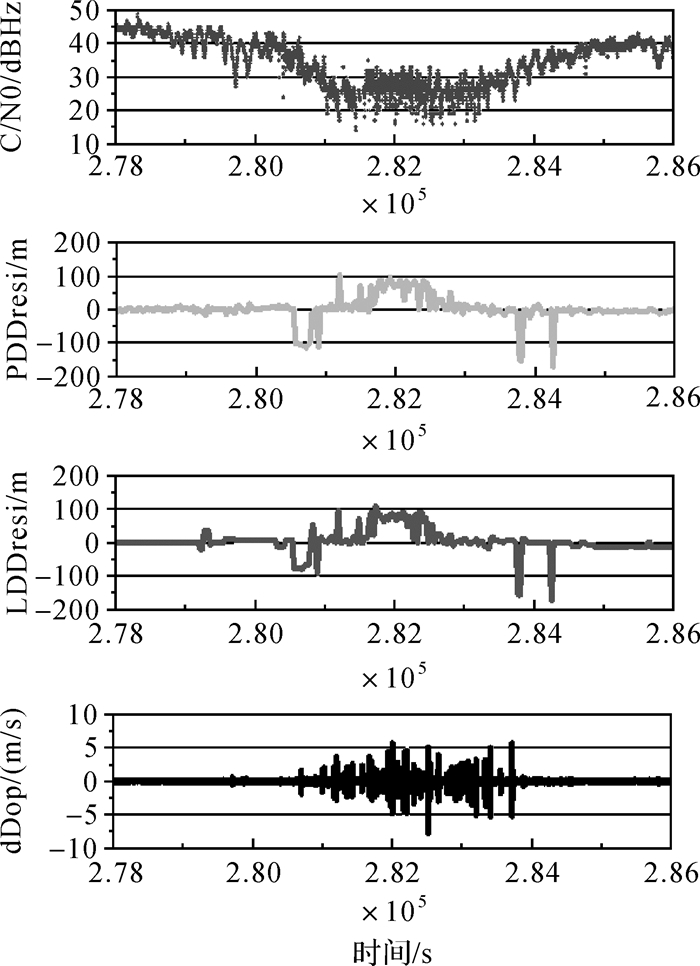
| 图 14 商场建筑物旁B07的载噪比、伪距双差残差、载波相位双差残差和多普勒历元差 |
可以看出,当GPS卫星的C/N0低于40 dBHz时,伪距残差存在几十米甚至300 m的异常,载波相位残差与伪距残差的变化趋势与大小基本一致,多普勒历元差也存在几米量级的波动。BDS卫星也出现类似情况。在这些异常情况下,卫星的C/N0甚至达到40 dBHz。对伪距和载波相位观测值的延迟影响一致,与NLOS信号的理论分析一致,说明在高楼附近,接收机接收到NLOS卫星信号。由于直射波被完全遮挡,接收机只接收到反射波,反射波信号功率会随着反射面的特性存在一定的减弱,从40 dBHz以上下降到20 dBHz以下,从而使伪距和载波出现频繁失锁现象,由于载噪比下降幅度较大,发生NLOS效应时多普勒观测值的噪声也明显增大。
4 结论本文采用双差方程提取伪距与载波相位多路径和NLOS信号延迟量,并在建筑物附近和树木遮挡两种典型的城市观测环境下,用UBLOX-NEO-M8T多系统单频导航型接收机进行静态数据采集,通过数据处理分析,可以得出以下结论:
(1) 对于UBLOX-NEO-M8T导航型接收机,载噪比较小时多普勒噪声明显增大。受多路径信号影响严重的环境下,C/N0低于30 dBHz,多普勒噪声开始变大;而受NLOS影响严重的环境下,在较大的C/N0,多普勒噪声仍然很大。
(2) 在树木遮挡时,主要受多路径效应的影响,引起伪距的误差量级在10~150 m,对相位和多普勒的影响不明显。
(3) 在高楼遮挡时,会出现NLOS信号干扰,对伪距和载波相位观测值的影响相同,延迟量大小与反射点的距离有关,可达几百米,对导航定位产生重要影响。
对于城市的大众行人导航用户来说,观测环境复杂多变,同一历元数据中会存在多个由多路径或NLOS引起的粗差数据,因此,通过分析和认识多路径和NLOS延迟误差的特性及其对伪距、载波相位和多普勒的影响差异,在定位估计之前剔除这些粗差数据的干扰,才能提高用户导航定位的精度和可用性。
| [1] | 吴雨航, 陈秀万, 吴才聪. 利用信噪比削弱多路径误差的方法研究[J]. 武汉大学学报(信息科学版), 2008, 33(8): 842–845. |
| [2] | 钟萍, 袁林果, 丁晓利. GPS多路径重复性试验研究[J]. 测绘科学, 2010, 35(2): 43–45, 26. |
| [3] | 戴吾蛟, 伍锡锈, 罗飞雪, 等. 一种利用增广参数Kalman滤波的GPS多路径效应处理方法[J]. 武汉大学学报(信息科学版), 2012, 37(4): 423–427. |
| [4] | 李川, 刘星, 石明旺, 等. GPS多路径误差特性分析及削弱方法[J]. 导航定位学报, 2017, 5(1): 103–107. |
| [5] | JIANG Z, GROVES P D. GNSS NLOS and Multipath Error Mitigation Using Advanced Multi-constellation Consistency Checking with Height Aiding[J]. International Technical Meeting of the Satellite Division of the Institute of Navigation, 2012, 137(1): 79–88. |
| [6] | WANG L, GROVES P D, ZIEBART M K. Multi-constellation GNSS Performance Evaluation for Urban Canyons Using Large Virtual Reality City Models[J]. Journal of Navigation, 2012, 65(3): 459–476. DOI:10.1017/S0373463312000082 |
| [7] | GROVES P D, JIANG Z. Height Aiding, C/N0 Weighting and Consistency Checking for GNSS NLOS and Multipath Mitigation in Urban Areas[J]. Journal of Navigation, 2013, 66(5): 653–669. DOI:10.1017/S0373463313000350 |
| [8] | HSU L. Analysis and Modeling GPS NLOS Effect in Highly Urbanized Area[J]. GPS Solutions, 2018, 22(1): 7. DOI:10.1007/s10291-017-0667-9 |
| [9] | BETAILLE D, PEYRET F, ORTIZ M, et al. A New Modeling Based on Urban Trenches to Improve GNSS Positioning Quality of Service in Cities[J]. IEEE Intelligent Transportation Systems Magazine, 2013, 5(3): 59–70. DOI:10.1109/MITS.2013.2263460 |
| [10] | HSU L, GU Y, HUANG Y, et al. Urban Pedestrian Navigation Using Smartphone-based Dead Reckoning and 3D Map-aided GNSS[J]. IEEE Sensors Journal, 2016, 16(5): 1281–1293. DOI:10.1109/JSEN.2015.2496621 |
| [11] | 谢钢. GPS原理与接收机设计[M]. 北京: 电子工业出版社, 2009. |
| [12] | GROVES P. GNSS Solutions:Multipath vs.NLOS Signals.How Does Non-line-of-sight Reception Differ from Multipath Interference[J]. GNSS Magazine, 2013, 8(6): 40–42. |
| [13] | CARCANAGUE S.Low-cost GPS/GLONASS Precise Positioning Algorithm in Constrained Environment[D].Toulouse: Institut National Polytechnique de Toulouse, 2013. http://www.mendeley.com/research/lowcost-gpsglonass-precise-positioning-algorithm-constrained-environment/ |
| [14] | WATSON J.High-sensitivity GPS L1 Signal Analysis for Indoor Channel Modelling[J].DOI: http://dx.doi.org/10.5072/PRISM/12074. |
| [15] | 贾有根, 李喆, 魏巍, 等.GPS信号在室内传播时的多普勒频移分析[C]//中国电机工程学会第十届青年学术会议.吉林: [s.n.], 2008. http://www.wanfangdata.com.cn/details/detail.do?_type=conference&id=7158763 |
| [16] | 唐小妹.高性能导航接收机中的载波恢复与载噪比估计研究[D].长沙: 国防科学技术大学, 2005. http://cdmd.cnki.com.cn/Article/CDMD-90002-2006126771.htm |