2. 大连舰艇学院海洋测绘工程军队重点实验室, 辽宁 大连 116018
2. Key Laboratory of Hydrographic Surveying and Mapping of PLA, Dalian Naval Academy, Dalian 116018, China
水下地形匹配定位是潜航器利用海底地形地貌的分布特征进行相关匹配运算,从而实现准确定位的方法[1]。该方法具有自主、隐蔽、全天候、定位精度与航程无关等优点[2],因而受到了国内外学者的广泛关注。
已有的研究表明,影响水下地形匹配定位的主要因素有:匹配区地形固有信息量的多少、匹配算法的优劣,以及地形匹配基准图的制备与选取[3-4]。其中,有关匹配区地形固有信息量及匹配算法的研究较多[5-10],针对地形匹配基准图的制备与选取的研究较少,尤其在合理选取航海图水深模型(digital depth model,DDM)作为水下地形匹配基准图时匹配定位是否可行,以及如何选取合理比例尺的航海图DDM作为匹配基准图以减少误匹配的发生,这些问题仍然缺乏必要的探讨。
为此,本文将系统分析不同比例尺的航海图DDM应用于水下地形匹配定位的可行性。首先,在经典TERCOM(terrain contour matching)算法的基础上,顾及航海图DDM水深点离散分布的特点,构建一种基于航海图DDM的水下地形匹配定位算法;然后,选取100个试验区构建比例尺从1:20 000到1:200 000的多组航海图DDM;最后,分别以这些航海图DDM作为地形匹配基准图进行匹配定位试验,并分析各比例尺下航海图DDM应用于水下地形匹配定位的可行性。
1 TERCOM匹配定位算法TERCOM算法的基本原理[8]是根据惯性导航系统(inertial navigation system,INS)推算的潜航器航迹点序列,在地形匹配基准图中选取与之平行的多组水平位置点序列作为潜航器可能的航迹,计算各组水平位置点序列对应的基准图水深序列,选择与实地测量的水深值序列相关性最好的一组序列,并将该序列对应的末端水平位置作为匹配结束时目标的匹配定位结果。
由此可见,TERCOM算法的核心内容主要包括2个方面:①根据INS求解基准图水深序列的算法;②在基准图水深序列中选取与实测水深序列匹配最优的算子。
1.1 基准图水深序列的求解现有的TERCOM算法及其改进算法多采用规则格网模型(regular grid model,RGM)作为地形匹配基准图;当采用航海图DDM作为地形匹配基准图时,由于航海图DDM的水深呈不规则离散分布,不同于水深规则分布的RGM,因此并不能将航海图DDM直接应用于现有算法。
为解决这一问题,本文通过以下几个步骤求解基准图水深序列上某一点(x, y)的水深值:
(1) 采用Delaunay三角网对航海图DDM的水深数据进行组织,并依次求解各三角形的重心[11]。
(2) 将各三角形的重心置于K-D树(K-Dimension tree)[12]中。
(3) 在K-D树中选择与点(x, y)最近的重心,并根据该重心快速求解点(x, y)所在的三角形。
(4) 采用具有较高精度和插值效率的三角线性内插算法求解点(x, y)的水深值z。
(5) 依此循环步骤(1)—步骤(4)求解基准图水深序列各点的水深值,构成待匹配的水深点序列。
其中,步骤(4)中水深值的计算公式为[13]
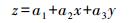 (1)
(1) 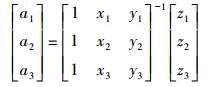 (2)
(2) 式中,z表示待求点(x, y)的水深值;(x1, y1)、(x2, y2)、(x3, y3)分别表示点(x, y)所在三角形的顶点坐标;z1、z2、z3分别表示三角形顶点对应的模型水深。
1.2 最优匹配的判别算子目前,TERCOM算法中较为常用的最优匹配判别算子有:MAD算子(mean absolute difference)、MSD算子(mean square difference)、互相关COR(cross correlation)算子和Hausdorff距离算子[14]等。本文将选择具有较好匹配性能的MSD算子[15]作为最优匹配的判别算子,其计算公式为
 (3)
(3) 式中,zi和z′i分别表示待匹配点的水深值与实测水深值;n表示水深点的个数。
2 试验与分析 2.1 试验区的选取与划分试验区的海底地形三维效果如图 1所示。其中,图 1(a)所示试验区1的水深平均距离约为5 m,水深最小值为42.85 m,水深最大值为131.74 m,水深值的标准差为13.8 m;图 1(b)所示试验区2的水深密度约为5 m,水深最小值为49.85 m,水深最大值为82.25 m,水深值的标准差为6.9 m。

|
| 图 1 试验区海底三维示意图 |
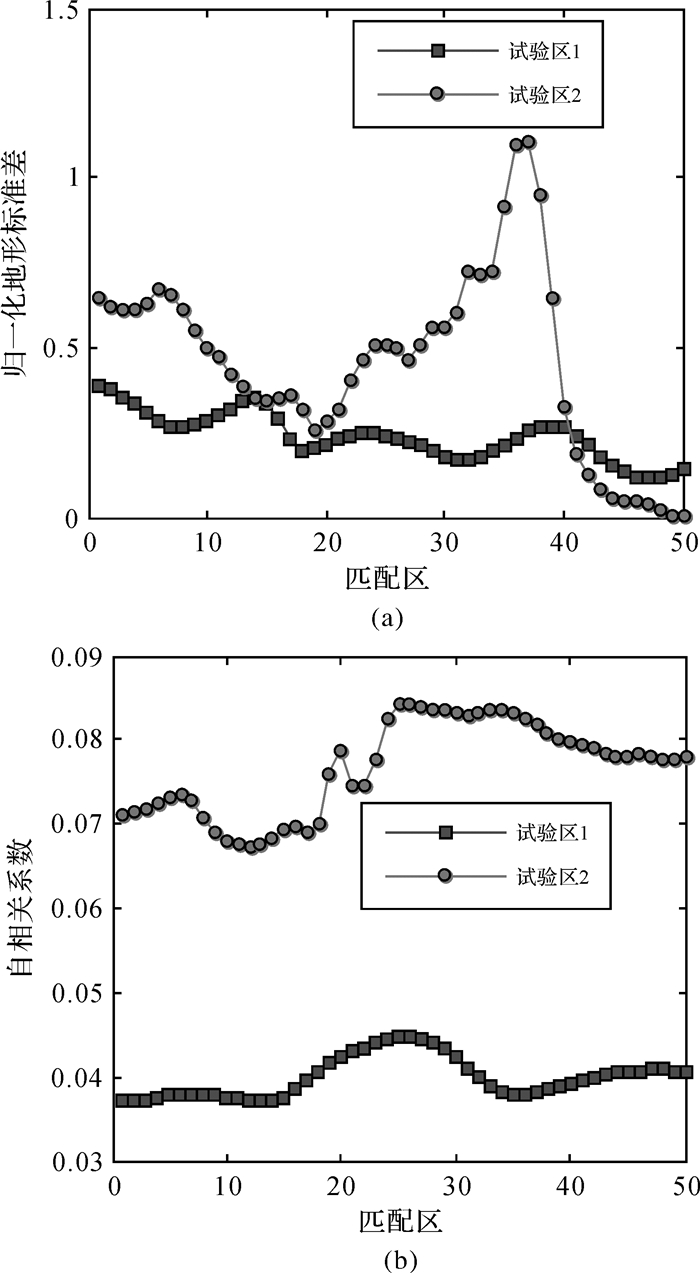
参照文献[13],按照“取浅舍深”“深浅兼顾”的原则对2块海区的水深数据进行处理,分别构建比例尺从1:20 000到1:200 000的32组航海图DDM;然后,将试验区1和试验区2分别均匀地划分为50份,共构成100个匹配区。这些匹配区的归一化地形标准差和自相关系数如图 2所示。
|
| 图 2 匹配区的特征参数分布 |
由图 2可知,试验区2中选取的50组匹配区归一化地形标准差及自相关系数均普遍大于试验区1;试验区1中的50个匹配区归一化地形标准差为0.115~0.39,各匹配区之间的差别较小;试验区2中的50个匹配区其归一化地形标准差为0.036~1.106,各匹配区之间的差别较大;试验区1的50个匹配区的其相关系数均小于0.05;试验区2的50个匹配区自相关系数均在0.06以上。
2.2 航海图DDM直接应用于匹配定位的可行性分析参照文献[16],地形匹配定位试验的基本参数设置为:进入地形匹配试验区时,UV的初始位置误差设为1060 m,航向误差为0;开始地形匹配时,UV的航速为10节,航向为0,陀螺随机游走为0.01°/h,加速度计精度为0.000 01 g/h,给水深增加振幅为水深值0.1%的非高斯噪声和水深值0.01%的系统噪声,水深采样频率为1/6 Hz。
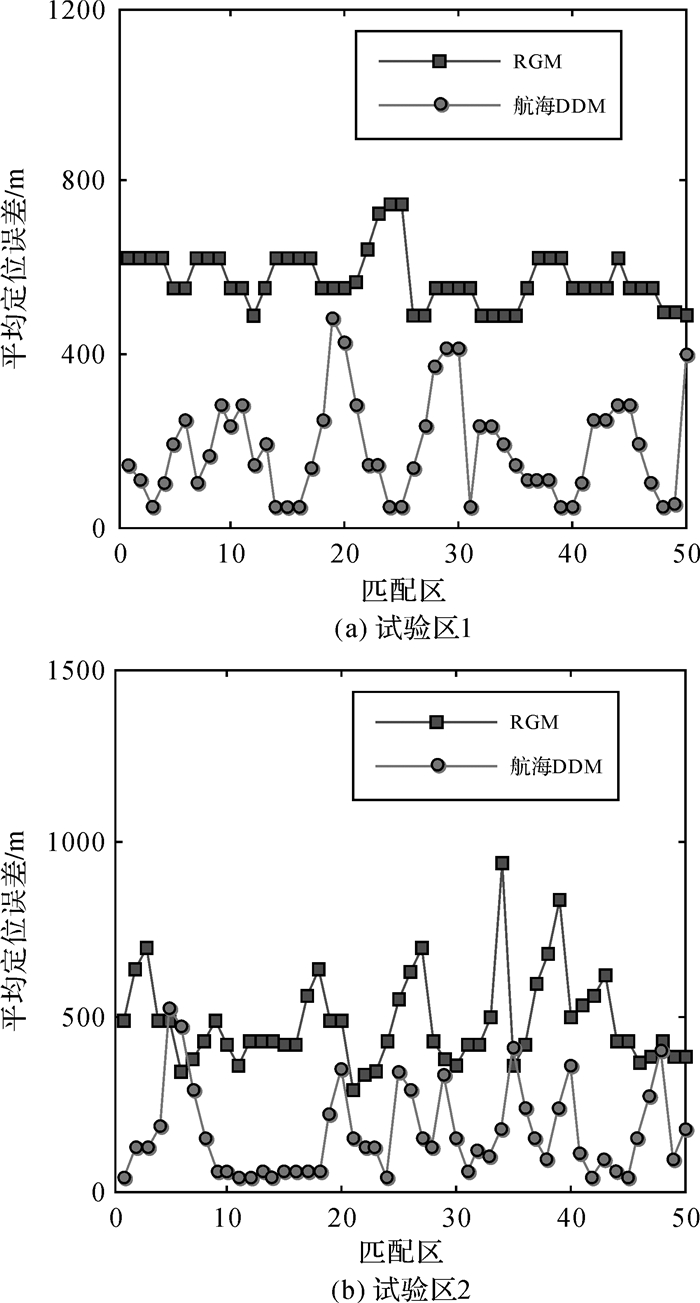
在以上参数设置的基础上,选取比例尺为1:25 000的航海图DDM作为匹配基准图;构建与1:25 000海图DDM水深节点数相当的RGM,并将采用RGM作为地形匹配基准图的试验作为对比试验,试验结果如图 3所示。
|
| 图 3 基于航海图DDM的定位可行性试验 |
由图 3分析可知,在以上的参数设置条件下,采用航海图DDM作为地形匹配基准图时,其平均定位误差要普遍小于采用RGM作为地形匹配基准图时的定位误差,且2组试验的定位误差均远小于1060 m。这说明,直接采用航海图DDM作为地形匹配基准图进行水下地形匹配定位是可行的,同时也能够有效降低潜航器的位置误差。
2.3 不同比例尺航海图DDM应用于匹配定位的对比分析在上节参数设置的基础上,分别基于比例尺不同的32个航海图DDM在100个匹配区中进行匹配定位试验,试验结果如图 4所示。其中,图 4(a)表示在试验区1中的50个匹配区中的定位试验结果,图 4(b)表示在试验区2中的50个匹配区中的定位试验结果。

|
| 图 4 不同比例尺航海图DDM的定位可行性试验 |
由图 4(a)可知,在试验区1中的50个匹配区进行匹配定位时,当比例尺大于1:60 000时,TERCOM算法的定位误差普遍在500 m以下(如图 4(a)中实线矩形);随着比例尺的减小,定位误差逐渐增加,大约在比例尺为1:75 000左右时开始出现误匹配(如图 4(a)中虚线矩形)。由图 4(b)可知,在试验区2的50个匹配区中进行匹配定位时,同样呈现随着比例尺的减小误匹配逐渐增多的趋势;在比例尺为1:40 000左右时,试验区2中的定位试验出现了误匹配(如图 4(b)中实线矩形),这一现象在比例尺小于1:125 000时尤其明显(如图 4(b)中虚线矩形)。为进一步定量描述各比例尺下误匹配发生的概率,本文给出了具体的统计结果,如图 5所示。
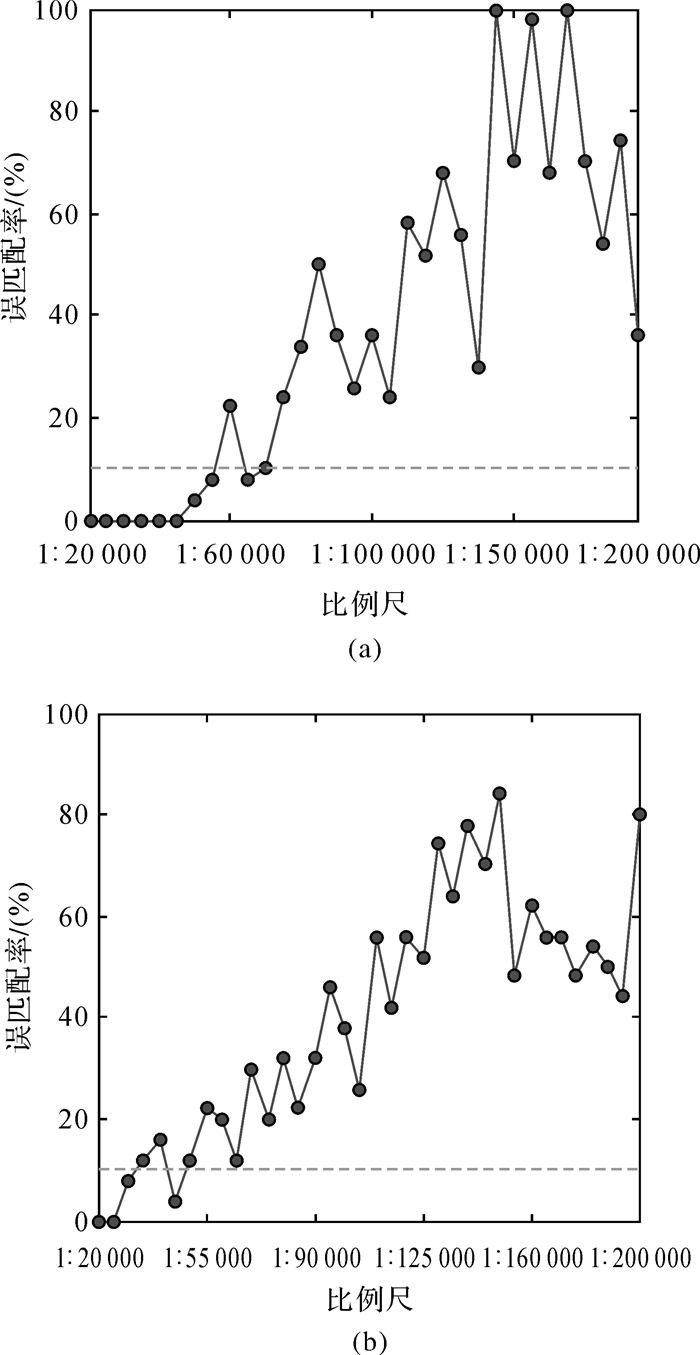
|
| 图 5 不同比例尺下的误匹配概率 |
由图 5可知,在试验区1和试验区2中进行匹配定位时,随着比例尺的降低,误匹配的概率逐渐增加。其中,在试验区1中进行匹配定位试验时,比例尺大于1:55 000时其误匹配的概率在10%以下,当比例尺大于1:50 000时没有误匹配发生;在试验区2中进行匹配定位试验时,比例尺大于1:30 000时误匹配的概率在10%以下,当比例尺大于1:25 000时没有误匹配的发生。因此,在采用航海图DDM作为水下地形匹配定位基准图时,为了减少误匹配的发生,应当选取比例尺大于1:25 000的航海图DDM。
3 结论通过分析、计算及试验比对,得出结论如下:
(1) 改进后的TERCOM算法可以直接以航海图DDM作为地形匹配基准图进行匹配定位。
(2) 统计结果表明,当航海图DDM的比例尺大于1:25 000时误匹配的现象较少发生,为减少误匹配发生的概率,应当优先选取比例尺大于1:25 000的航海图DDM作为地形匹配基准图。
当然,限于文章篇幅,本文只是基于TERCOM算法讨论了航海图DDM应用于水下地形匹配定位的可行性,并没有对采用其他定位算法的可行性进行分析;此外,相比采用RGM作为匹配基准图的算法,由于本文算法采用了TIN模型对航海图DDM进行组织,匹配算法的效率必然有所降低,这些问题都有待于在以后的研究中进一步完善。
| [1] | 谭佳琳. 粒子群优化算法研究及其在海底地形辅助导航中的应用[D]. 哈尔滨: 哈尔滨工程大学, 2010. |
| [2] | 程传奇, 郝向阳, 张振杰, 等. 鲁棒性地形匹配/惯性组合导航算法[J]. 中国惯性技术学报, 2016, 24(2): 202–207. |
| [3] | 刘强, 徐晓苏. 海底地形数据网格化方法研究[J]. 舰船电子工程, 2013, 33(5): 59–61, 64. DOI:10.3969/j.issn.1627-9730.2013.05.020 |
| [4] | 张毅, 高永琪, 梁锦强. 水下地形匹配导航中的地形可导航性分析[J]. 四川兵工学报, 2013, 34(11): 55–58, 76. DOI:10.11809/scbgxb2013.11.017 |
| [5] | 张凯, 赵建虎, 王锲. 基于支持向量机的水下地形匹配导航中适配区划分方法研究[J]. 大地测量与地球动力学, 2013, 33(6): 72–77. |
| [6] | 饶喆, 张静远, 冯炜. 一种地形匹配导航区域的可导航性评价方法[J]. 河南大学学报(自然科学版), 2016, 46(1): 89–95. DOI:10.3969/j.issn.1003-4978.2016.01.011 |
| [7] | 张凯, 赵建虎, 张红梅. 一种基于M估计的水下地形抗差匹配算法[J]. 武汉大学学报(信息科学版), 2015, 40(4): 558–562. |
| [8] | ZHAO L. An Algorithm for Terrain-aided Inertial Navigation Based on Nonlinear Optimal Filtering[J]. Science China-physics Mechanics & Astronomy, 2011, 54(6): 1083–1088. |
| [9] | ZHANG K, LI Y, ZHAO J, et al. A Study of Underwater Terrain Navigation based on the Robust Matching Method[J]. Journal of Navigation, 2014, 67(4): 569–578. DOI:10.1017/S0373463314000071 |
| [10] | 张静远, 谌剑, 李恒, 等. 水下地形辅助导航技术的研究与应用进展[J]. 国防科技大学学报, 2015, 37(3): 128–135. |
| [11] | 张春亢, 赵学胜, 王洪斌. 一种采用流计算的Delaunay三角网切块剖分算法[J]. 武汉大学学报(信息科学版), 2017, 42(3): 1–7. |
| [12] | 陈茂霖, 万幼川, 田思忆, 等. 一种基于线性KD树的点云数据组织方法[J]. 测绘通报, 2016(1): 23–27. |
| [13] | 贾帅东. 航海图DDM的构建理论与方法[D]. 大连: 海军大连舰艇学院, 2015. |
| [14] | 赵建虎, 王胜平, 王爱学. 一种改进型TERCOM水下地磁匹配导航算法[J]. 武汉大学学报(信息科学版), 2009, 34(11): 1320–1323. |
| [15] | 闫利, 崔晨风, 吴华玲. 基于TERCOM算法的重力匹配[J]. 武汉大学学报(信息科学版), 2009, 34(3): 261–264. |
| [16] | 王巍. 惯性技术研究现状及发展趋势[J]. 自动化学报, 2013, 39(6): 723–729. |


