合成孔径雷达干涉测量(interferometric synthetic aperture radar,InSAR)技术以其高精度、高空间分辨率的地表形变监测能力,目前已经被广泛应用于监测各种因素导致的地表形变[1-7]。随着越来越多的卫星发射升空,同一地区可以获取多种不同传感器SAR影像,进而可以获取不同雷达视线向地表形变监测结果(多视线向D-InSAR形变量)。将多视线向D-InSAR地表形变量作为观测量,以卫星轨道方位角和入射角等参数构建系数矩阵,建立三维地表形变解算模型,可以获取真实三维地表形变[12]。然而,由于受到不同误差因素的影响,多视线向D-InSAR地表形变监测结果的精度不尽相同。因此,基于多视线向D-InSAR形变量联合平差,以获取高精度三维形变解算结果尤为重要。其研究关键点是如何合理确定各观测量的权重。
本文提出一种基于GPS约束的多视线向D-InSAR三维地表形变解算中定权方法。该方法以高精度GPS形变监测结果作为约束,通过对多视线向D-InSAR观测值进行评价确定其权重。本文以2009年意大利L’Aquila地震三维地表形变解算为例,采用GPS约束的定权方法实现三维形变解算。试验结果表明,本文提出的GPS约束定权的多视线向D-InSAR三维形变解算方法可获取更可靠的解算结果,可以解决不同精度观测量联合平差权重确定存在的定权难、定权适用性差、精度低等突出问题。
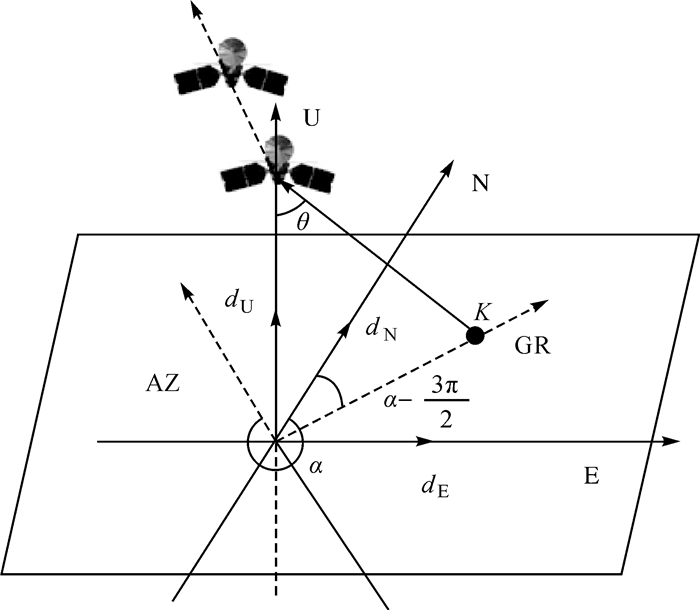
1 多视线向D-InSAR三维地表形变GPS约束定权方法 1.1 多视线向D-InSAR三维地表形变解算SAR卫星的成像几何关系如图 1所示。AZ向表示卫星飞行方向在地面上的投影,GR向表示卫星视线向在地面的投影,α表示卫星方位角,θ表示SAR影像入射角,U、E和N分别代表大地测量坐标系中的垂直、东西和南北方向,dU,dE和dN分别代表对应方向上的形变信息。
|
| 图 1 SAR卫星三维成像示意图 |
现用d=[dUdEdN]T表示三维地表形变信息,R=[RLOS1RLOS2RLOS3RLOS4]T表示雷达坐标系中不同视线向形变信息,建立如下形变模型
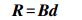 (1)
(1) 式中,B为三维形变模型系数矩阵,具体可以表示为
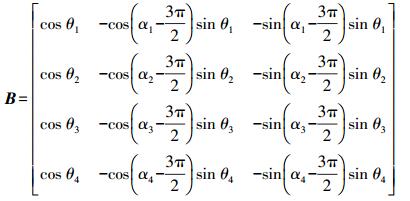 (2)
(2) 根据最小二乘原理,可以解算出三维形变信息
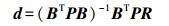 (3)
(3) 式中,P为观测量的权重,具体可以表示为P=diag((1/σLOS1)2, (1/σLOS2)2, (1/σLOS3)2, (1/σLOS4)2),diag()表示对角阵,σLOS1、σLOS2、σLOS3和σLOS4分别表示RLOS1、RLOS2、RLOS3和RLOS4的标准差。
1.2 基于GPS约束的定权方法针对多视线向D-InSAR三维地表形变解算中存在的定权问题,本文提出以GPS精密形变观测量为基准数据,对多视线向D-InSAR观测量进行精度评价,综合估算出轨道和地形误差及噪声等因素引起的误差。由于GPS测站数量有限,无法逐像元进行精度评价。顾及轨道和地形及噪声等因素引起的误差对形变监测结果影响的特点,建立联合拟合模型并计算拟合参数。根据确定出的拟合模型估算多视线向D-InSAR每个像元观测量的方差,以计算出的方差的倒数确定权矩阵,建立加权最小二乘三维地表形变解算模型。具体步骤如下:
(1) 将GPS三维形变观测量换算到D-InSAR视线方向,如下
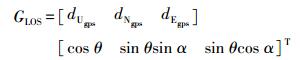 (4)
(4) (2) 根据双观测值之差标准差计算公式,计算出GPS测站对应D-InSAR观测量方差
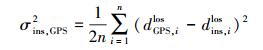 (5)
(5) 式中,n为GPS观测站个数;σins, GPS2为第i个GPS观测站对应的D-InSAR测量方差;dGPS, ilos为第i个GPS观测站三维形变观测量换算到D-InSAR视线向形变量;dins, ilos为第i个GPS观测站对应的像元D-InSAR视线向形变量。
(3) 根据步骤(2)计算出的双观测值之差标准差及对应像元相干值,按照下式计算方差
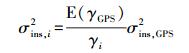 (6)
(6) 式中,γi为第i个像元相干系数;E(γGPS)为GPS观测站对应的SAR影像像元相干系数均值。
(4) 以步骤(3)估算出的D-InSAR像元的方差为依据,充分考虑轨道和地形误差对形变量影响的特点,建立方差与像元点的位置和高程联合拟合模型
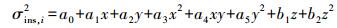 (7)
(7) 式中,等号右侧前6项为轨道误差项;x表示第i个像元方位向坐标;y表示第i个像元距离向坐标;后两项表示地形误差项,z表示坐标为(x, y)像元的高程值,ai(i=1, 2, …, 5)和bj(j=1, 2)分别表示待估参数。
估算出上式中系数参数后便可以确定出拟合模型,按照上述模型估算每个像元D-InSAR形变监测结果方差。
(5) 根据D-InSAR形变监测结果方差,按照下式定权
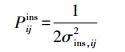 (8)
(8) 按照式(8)计算出权阵P之后,按照式(3)进行三维地表形变解算。
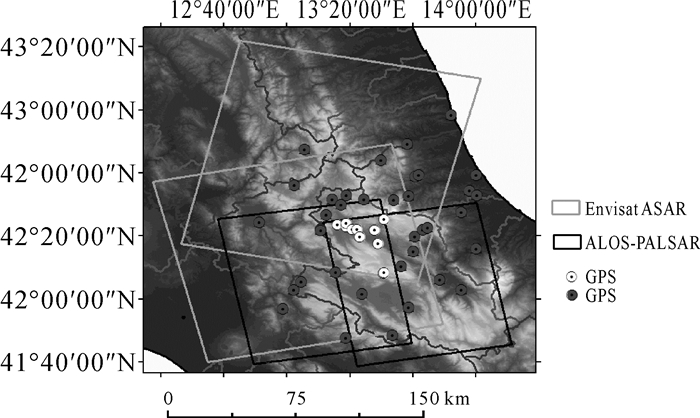
2 L’Aquila地震多视线向D-InSAR地表形变监测 2.1 试验区与数据源2009年4月6日意大利中部城市L’Aquila发生了Mw6.3级地震,整个意大利中部地区均有震感。本文以该地震震中区域为研究区验证定权方法的有效性。考虑干涉对的选取原则(足够短的垂直基线和时间基线),选取了4个干涉像对SAR数据,分别用P1、P2、P3和P4表示,影像覆盖范围如图 2所示。同期的GPS数据来源于文献[13]。研究区范围内共有48个点,如图 2所示,其中黑点表示用来估算联合拟合模型参数的GPS数据,白点用来验证解算精度。
|
| 图 2 研究区概况 |
以震前、后获取的SAR影像分别作为主、辅影像,采用双轨D-InSAR技术对数据进行处理,对主、辅影像进行配准、重采样和共轭相乘处理,获取干涉相位图。采用30 m分辨率的SRTM DEM数据去除地形相位的影响。采用Goldstein滤波方法对干涉图进行噪声滤除,获取最终的干涉图。采用最小费用流的方法进行相位解缠。解缠之后的干涉图只包含形变相位、大气相位和残余噪声相位。其中,大气相位对干涉图的影响主要体现在对流层延迟方面,往往跟地形高程有一定的相关性,通过GAMMA软件的相关算法可以一定程度上去除大气误差相位。
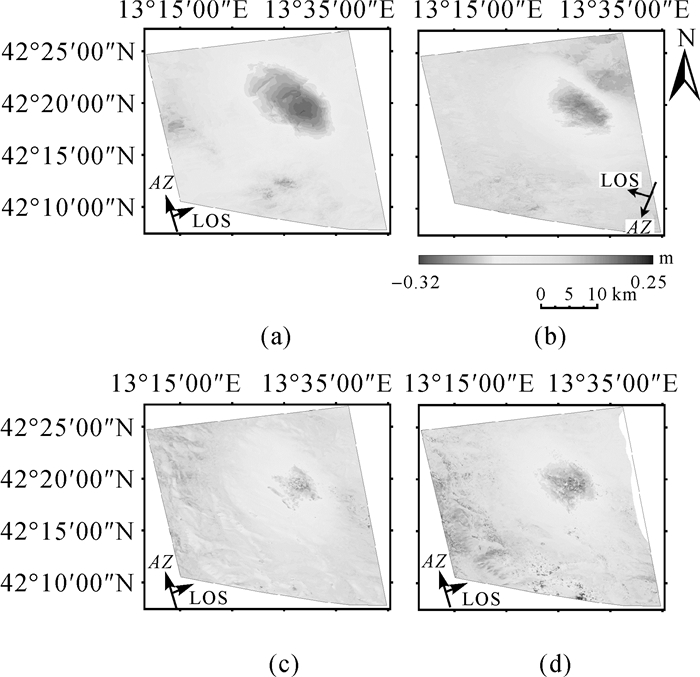
图 3为地理编码后的形变图。从图中可以看出,多视线向D-InSAR形变监测结果在形变趋势和量级上基本一致,震中和断裂带周边形变为负值表示该区域地面下沉(呈现深色)。多视线向D-InSAR形变监测结果在雷达视线向上下沉的一致性说明拉奎拉地震是以地表下沉为主。根据地质调查的结果显示,拉奎拉地区所在的阿尔卑斯地区断层走向为西北-东南方向,大小在40~50之间的西南倾向,正断层。
|
| 图 3 不同轨道SAR影像获取的形变图 |
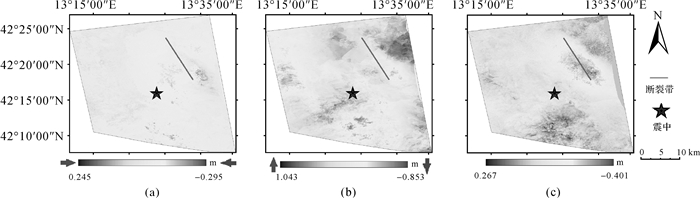
获取了多视线向D-InSAR地表形变信息,按照第一部分介绍的数据处理方法进行三维地表形变解算。值得注意的是两种数据形变监测结果具有不同的空间分辨率,本文将ASAR数据监测结果重采样至ALOS数据分辨率。入射角和方位角信息见表 1。用来计算拟合参数的GPS数据具体分布如图 2中白色点所示。解算出的三维地表形变结果如图 4所示。
| 序号 | 传感器 | 升、降轨情况 | 轨道 | 干涉对获取时间 | 垂直基线/m | 方位角/(°) |
| P1 | ENVISAT-ASAR | A | 401 | 2009-02-23 2009-05-04 | 141 | 346.5 |
| P2 | ENVISAT-ASAR | D | 79 | 2008-04-27 2009-04-12 | 46 | 193.5 |
| P3 | ALOS-PALSAR | A | 833 | 2008-07-03 2009-05-21 | 353 | 349.7 |
| P4 | ALOS-PALSAR | A | 840 | 2008-07-20 2009-04-22 | 201 | 349.7 |
|
| 图 4 三维地表形变解算结果 |
从解算出的三维地表形变结果中可以看出,在震中主形变区内,地表发生了东南方向的水平错动。在断层周边的三维形变场中表现出了比较明显的形变特征。在东西方向形变场的下半部分,地表向西发生了移动,上侧发生了向东的移动,表现出比较明显的形变错动。在南北方向下半部分,地表向北发生了移动,上侧发生了向南的移动,同样表现出比较明显的形变错动。在垂直方向的右上方,地表表现为上升的运动,而在下方表现为沉降,垂直方向上也发生了明显了错动。
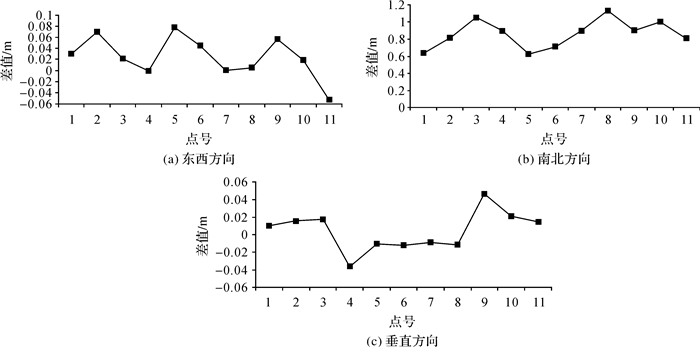
3.2 精度验证为了说明本文提出定权方法的有效性,通过解算出的三维结果与真实GPS数据进行对比。GPS点的位置如图 2白点位所示。将解算结果与GPS数据的作差值比较。图 5给出了对比结果,曲线越接近于0说明解算结果越准确。
|
| 图 5 结果对比 |
从图 5可以看出,相对于南北方向来说,东西方向和垂直方向2个方向的纵坐标取值范围小,这说明东西和垂直向的解算精度比南北方向高(纵轴表示与GPS监测出的三维形变的差值)。导致这一结果的原因有两点:①卫星近南北方向飞行,导致雷达视线向对南北方向形变不敏感,在解算过程中观测值中的噪声被放大,从而导致南北方向解算精度差[17];②GPS监测结果出垂直向精度比水平方向监测精度要差[18],这会对GPS约束改进定权方法解算结果产生影响。
为了进一步说明本文提出定权方法的有效性,表 2计算解算出的三维地表形变与收集的GPS三维地表形变对比的均方根误差(RMSE)及统计了对比的最大差值。
本文针对多视向D-InSAR三维地表形变解算定权问题,提出了一种基于GPS约束的多视线向D-InSAR三维地表形变监测定权方法。以2009年拉奎拉地震实测数据为例进行了可行性验证,可以得出以下结论:
(1) 两种数据监测出的研究区形变结果基本一致,但两种数据获取的时间间隔、数据轨道和波段会导致监测结果在形变位置、范围、形变量等方面略有不同。
(2) 从解算出的三维地表形变分布图来看,垂直方向和东西方向的解算结果相对较高,南北方向解算结果受噪声影响较大。
(3) 相对于东西方向来说,垂直方向的均方误差较大,解算精度差一些,这表明GPS低精度的垂直方向形变监测结果会对三维形变解算精度产生影响。
(4) 通过收集到的GPS监测数据对解算结果进行精度分析与验证,对比发现解算出的东西方向均方根误差为0.036 4 m,南北方向均方根误差为0.513 5 m,垂直方向均方根误差为0.439 m。
综上所述,利用本文所提出的GPS约束定权方法能正确确定多视线向D-InSAR观测量的权,且计算简单。采用GPS约束改进定权方法能提高三维解算精度。
| [1] | 殷跃平, 张作辰, 张开军. 我国地面沉降现状及防治对策研究[J]. 中国地质灾害与防治学报, 2005, 16(2): 1–8. DOI:10.3969/j.issn.1003-8035.2005.02.001 |
| [2] | YOUNG W. The Southern California Integrated GPS Network (SCIGN)[J]. Bulletin of the Seismological Society of America, 2007, 96(1): 90–106. |
| [3] | SAGIYA T. A Decade of GEONET:1994-2003 the Continuous GPS Observation in Japan and Its Impact on Earthquake Studies[J]. Earth, Planets and Space, 2004, 56(8): xxix–xli. DOI:10.1186/BF03353077 |
| [4] | MASSONNET D, ROSSI M, CARMONA C, et al. The Displacement Field of the Landers Earthquake Mapped by Radar Interferometry[J]. Nature, 1993, 364(6433): 138–142. DOI:10.1038/364138a0 |
| [5] | GORUM T, FAN X, WESTEN C J, et al. Distribution Pattern of Earthquake-induced Landslides Triggered by the 12 May 2008 Wenchuan Earthquake[J]. Geomorphology, 2011, 133(3): 152–167. |
| [6] | LU Z, MASTERLARK T, DZURISIN D. Interferometric Synthetic Aperture Radar Study of Okmok Volcano, Alaska, 1992-2003:Magma Supply Dynamics and Postemplacement Lava Flow Deformation[J]. Journal of Geophysical Research:Solid Earth, 2005, 110(B2). |
| [7] | HILLEY G E, BVRGMANN R, FERRETTI A, et al. Dynamics of Slow-moving Landslides from Permanent Scatterer Analysis[J]. Science, 2004, 304(5679): 1952–1955. DOI:10.1126/science.1098821 |
| [8] | YE X, KAUFMANN H, GUO X F. Landslide Monitoring in the Three Gorges Area Using D-InSAR and Corner Reflectors[J]. Photogrammetric Engineering and Remote Sensing, 2004, 70(10): 1167–1172. DOI:10.14358/PERS.70.10.1167 |
| [9] | GOLDSTEIN R M, ENGELHARDT H, KAMB B, et al. Satellite Radar Interferometry for Monitoring Ice Sheet Motion:Application to an Antarctic Ice Stream[J]. Science, 1993, 262(5139): 1525–1525. DOI:10.1126/science.262.5139.1525 |
| [10] | BELL J W, AMELUNG F, FERRETTI A, et al. Permanent Scatterer InSAR Reveals Seasonal and Long-term Aquifer-system Response to Groundwater Pumping and Artificial Recharge[J]. Water Resources Research, 2008, 44(2): 1–18. |
| [11] | CARNEC C, DELACOURT C. Three Years of Mining Subsidence Monitored by SAR Interferometry, near Gardanne, France[J]. Journal of applied geophysics, 2000, 43(1): 43–54. DOI:10.1016/S0926-9851(99)00032-4 |
| [12] | HU J, LI Z W, ZHU J J, et al. Inferring Three-dimensional Surface Displacement Field by Combining SAR Interferometric Phase and Amplitude Information of Ascending and Descending Orbits[J]. Science China Earth Science, 2010, 53(4): 550–560. DOI:10.1007/s11430-010-0023-1 |
| [13] | CHELONI D, D'AGOSTINO N, D'ANASTASIO E, et al. Coseismic and Initial Post-seismic Slip of the 2009 mw 6.3 L'Aquila Earthquake, Italy, from GPS Measurements[J]. Geophysical Journal International, 2010, 181(3): 1539–1546. |
| [14] | HU J, LI Z W, LI J, et al. 3D Movement Mapping of the Alpine Glacier in Qinghai-Tibetan Plateau by Integrating D-InSAR, MAI and Offset-tracking:Case Study of the Dongkemadi Glacier[J]. Global and Planetary Change, 2014, 118(4): 62–68. |
| [15] | GE L. Integration of GPS and Radar Interferometry[J]. GPS Solutions, 2003, 7(1): 52–54. DOI:10.1007/s10291-003-0048-4 |


