数字道路信息是我国基础地理信息的重要组成部分,在城市规划、智能交通、紧急救援与位置服务等诸多领域扮演着至关重要的角色,应用系统运行的效率与效果和数字道路信息的准确性、详细程度及现势性息息相关。目前,数字道路信息通常由专业公司制作与维护,大多使用配置高精度GPS接收设备的专业测量车来采集与编辑,不仅费用昂贵,而且难以及时更新,其数字道路信息往往滞后于道路的最新变化。随着遥感技术的发展,许多学者提出了基于遥感影像和LiDAR数据的道路提取方法[1-4],但由于遥感影像与点云数据中混合了多种地物信息,道路提取容易受到干扰。此外,遥感影像与点云数据的获取成本较高,同样存在滞后问题。
随着定位技术、通信技术的不断发展成熟,获取移动对象的连续定位信息不再困难,很多普通车辆都配备了GPS设备。汽车的GPS轨迹能够反映道路的地理位置和几何结构。因此,从易于采集且每天更新的出租车GPS数据中提取道路信息成为研究热点。这种方法具有成本低廉、覆盖面大、易于获取、现势性强等优点。在基于轨迹数据提取道路信息的研究中,Liu基于几何距离与方向差异来聚类线段,然后通过拟合点簇来得到道路线[5];而Karagiorgou根据速度阈值,将轨迹数据划分为低、中、高速三类,分别聚类以得到相应道路结构,之后进行融合操作[6]。根据采样点的密集程度,将轨迹数据转化为栅格图,在此基础上利用Voronoi图或形态学等方法来提取道路中心线[7-9]。此外,Fathi利用已有道路地图来训练形状描述符,以区分交叉口与非交叉口[10];而唐炉亮根据时空认知的一些规律,利用Delaunay三角网融合不断插入新轨迹的方式获取道路信息[11]。
本文提出一种基于低频低精度车辆GPS轨迹数据的道路交叉口和中心线提取方法,首先,栅格化车辆轨迹数据得到轨迹图像,运用数学形态学滤波填补空洞、去除噪声、平滑表面,最后利用数学形态学细化方法获取道路中心线,进而提取道路交叉口。由于车辆GPS往往分布不均,为尽可能多提取GPS采样点分布稀疏区域的道路交叉口,在轨迹数据栅格化时生成多分辨率图像,分别处理获取道路交叉口,再将提取结果融合。其次,使用Douglas-Peukcer算法化简由数学形态学细化获取的道路中心线,使其与真实道路形状更加接近。
1 轨迹数据栅格化轨迹数据是由一系列连续的点坐标构成的,其栅格化本质上便是点栅格化。栅格数字图像可以定义为一个二维函数f(x, y),其中x和y是空间坐标,而在任意一对空间坐标(x, y)上的函数值f称为该点的强度或灰度,当x、y和f均为有限的离散数值时,称该图像为数字图像[12]。为了将轨迹点数据栅格化为数字图像,必须确定x、y、f的值。轨迹点数据的经纬度坐标plon和plat可以转换为数字图像的平面坐标x和y,转换的方法为
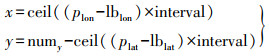 (1)
(1) 式中,lblon和lblat分别表示目标区域的最小经纬度;ceil()函数的功能是向上取整;interval表示每1度包含的像素个数,该变量确定了最终栅格图像的分辨率;numy表示目标区域y方向的像素个数,可以表示为
 (2)
(2) rtlat是目标区域最大经度,y方向的坐标之所以需要被numy减去是因为屏幕坐标系的原点在屏幕左上角。确定了坐标对(x, y),便可以为其赋强度值。一种简单的赋值方式是凡轨迹点所在的位置相应的栅格图像像素值设为1,否则设为0。由于低频低精度的出租车GPS轨迹数据包含大量的噪声点,如果以这样的方式简单处理,许多噪声处也将被误认为是道路像素点,增加了后续处理的难度。为了尽可能地减小噪声的影响,每个像素设定一个统计量c,规定当某个轨迹点落入栅格图像某像素时,该像素的c值加1。若c最终大于等于阈值,便将该像素值设为1,否则为0。此阈值设置越大,得到的道路像素点可信度越高,但也更可能导致轨迹数据稀疏区域道路像素点过少,因此阈值大小的选择应该视数据的情况而定。
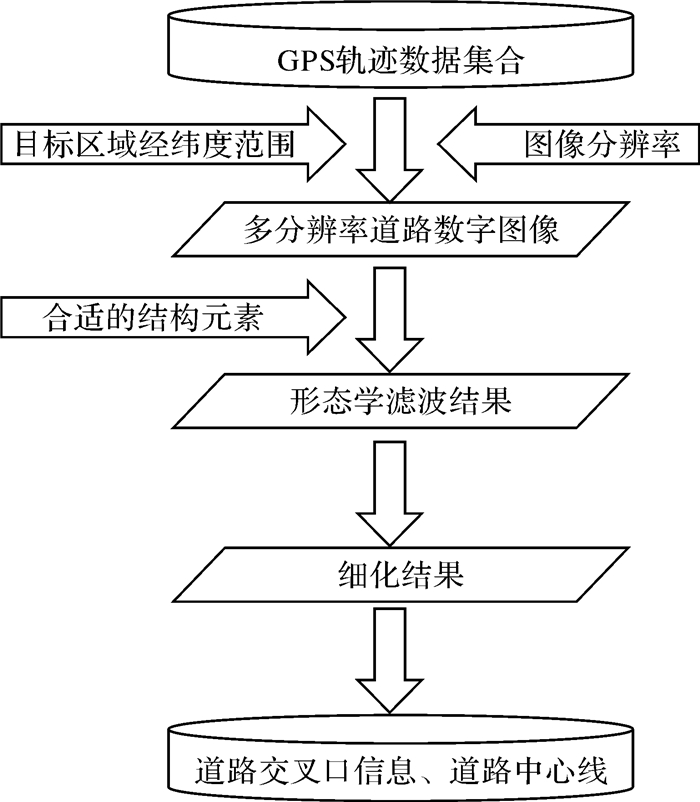
2 基于数学形态学的道路中心线与交叉口提取基于数学形态学的道路中心线与交叉口提取的过程包括:车辆轨迹数据栅格化、轨迹栅格数字图像形态学滤波、轨迹栅格数字图像细化、提取道路交叉口。如图 1所示。
|
| 图 1 基于数学形态学的道路交叉口提取的过程 |
栅格化大量低频低精度轨迹数据存在以下问题:①由于数据量大,栅格化结果难免出现孤立点和孔洞;②图像中要素的边缘不齐整,存在锯齿状凹凸不平的情况。这些问题均会对道路中心线的提取产生不良影响。本节使用数学形态学去除噪声、平滑对象表面。
数学形态学重构的方法可以消除孤立点、填补孔洞。数学形态学重构包含一个迭代膨胀的过程,利用这一点,只要施以一定的策略,便能填补孔洞。而重构作腐蚀运算可以在保证对象形状不变的情况下消除小对象。
数学形态学闭运算和开运算具有平滑图像的作用。闭运算可以消除狭窄的间断,填补断裂,对于轨迹栅格图像来说,可以填平对象表面的凹槽。此外,闭运算操作对采样点稀疏区域具有一定强化作用。开运算可以过滤突出物,能消除对象边缘毛刺,使其轮廓光滑。鉴于轨迹栅格图中对象表面凹凸不平,单独利用开运算或闭运算只能解决部分问题,通过使用混合滤波器结合两种运算的优点则会得到更好的结果。如图 2所示,闭运算和开运算处理如图 2(a)所示,依次得到的结果如图 2(b)和图 2(c)所示,最后使用数学形态学细化方法处理轨迹栅格图,得到道路中心线,如图 2(d)所示。

|
| 图 2 使用数学形态学处理轨迹栅格 |
交叉口是超过两条道路段相会的区域,是重要的路网信息。道路在图像中是线状对象,交叉口是不同道路的交点,反映在道路影像上便是不同线对象的交点。上节细化得到的道路中心线宽度仅为一个像素。遍历所有像素,计算每个像素8领域内像素点的个数,超过两个即可以判定它为交叉口像素,以此提取道路交叉口。
经过数学形态学去噪、平滑和增强的处理,获取的交叉口已经较为准确。然而某些区域轨迹采样点分布稀疏,去噪和平滑操作可能导致图像中部分轨迹被误清除,本文提出的多分辨率轨迹栅格图像提取交叉口的方法,在尽可能保持提取结果准确的前提下,提取尽可能多的交叉口。
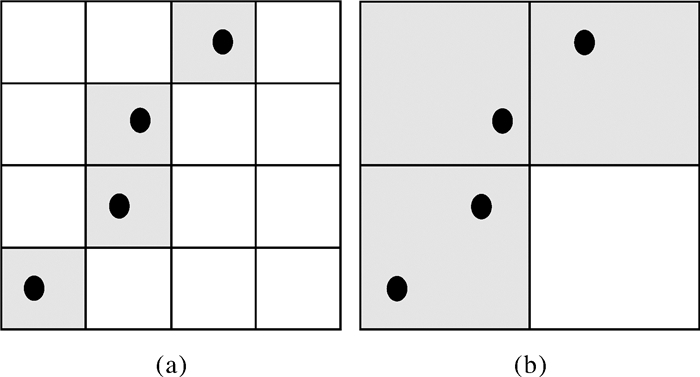
对轨迹点数据栅格化时,轨迹栅格图像的分辨率选择会影响最终提取结果。如果分辨率设置较高,如图 3(a)所示,可以更准确地反映道路所在位置,但轨迹像素点占整体像素总数的比例较少。对于轨迹点分布稀疏区域而言,这样的处理可能会产生更多的孤立点,并被当做噪声去除。如果分辨率设置较低,如图 3(b)所示,轨迹像素点占整体像素总数比例会增大。这有利于稀疏区域增强,但可能导致提取交叉口的位置不够准确。因此本文设置两种分辨率分别提取道路交叉口,并将它们的结果融合。融合的原则是保留高分辨率图像提取的全部交叉口,融合低分辨率图像提取的稀疏区域交叉口。
|
| 图 3 图像分辨率对栅格化的影响 |
Douglas-Peukcer算法[13]是线状要素化简的经典算法,主要思想是为复杂的多线段(polyline)寻找到组成点更少的相似简单多线段。其基本思路为:连接多线段的首末节点形成一条虚直线,求多线段所有节点到此直线的距离,寻找出最大距离值dmax。比较dmax与阈值限差D,若dmax<D,舍弃这条多线段上所有中间点;若dmax≥D,保留dmax相应的坐标点,并以该点为界,将多线段分为两部分,对这两部分递归使用该方法。
数学形态学细化结果基本能够反映道路的位置和形状,但是仍然存在歪扭的情况。将其矢量化并运用Douglas-Peukcer算法化简,可以使结果更接近真实的道路。不仅如此,移除部分多余点,还具有数据压缩和消除冗余细节的作用。
4 试验与分析试验以武汉市2014年5月29日—6月7日共10 d的出租车轨迹数据为数据源,大小约为2 GB,每条轨迹的采样间隔大于40 s。选择武汉市洪山广场附近约24 km2的城市核心区域为试验区域,试验环境为Windows 8 64位操作系统,开发工具为Matlab。
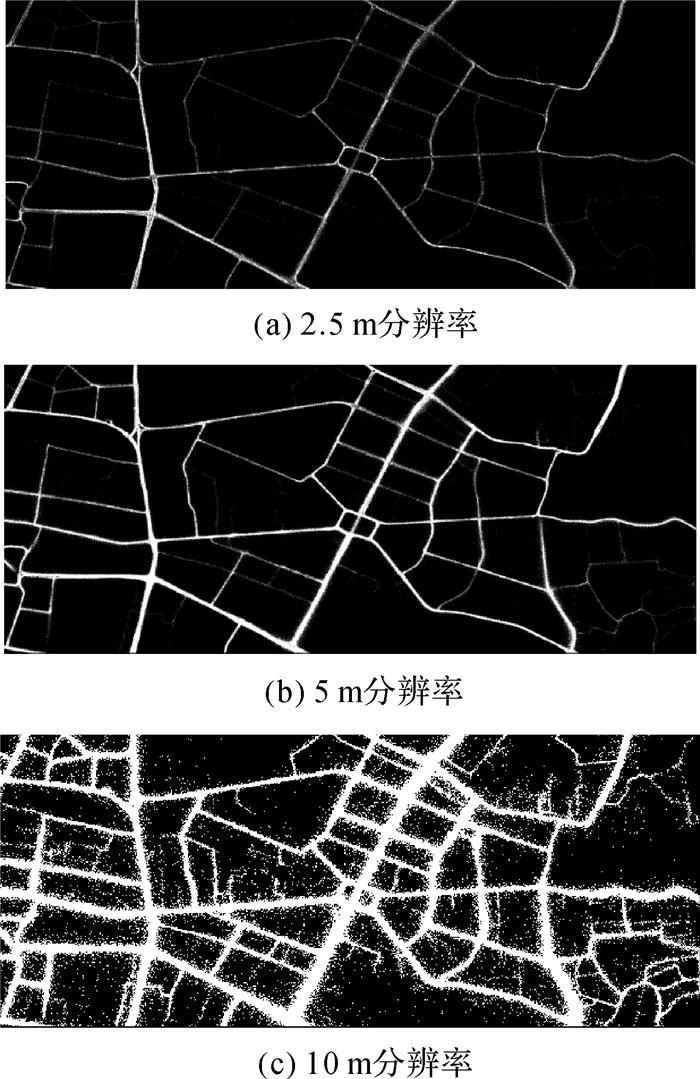
城市道路宽度具有多样化特点,既有宽度30~40 m的主干道,又有10~15 m的次要道路。为了能够准确反映所有道路的位置,并减少噪声的影响,栅格化的分辨率不宜选取太小。当分辨率设置为2.5、5和10 m时,结果如图 4所示。
|
| 图 4 轨迹点栅格化结果 |
由结果可知分辨率为10 m时,噪声严重影响了轨迹图像的质量,显然分辨率过小会导致结果不够准确。因此本文选择2.5和5 m两种分辨率的轨迹栅格图像,并用以下流程处理轨迹栅格图像:①数学形态学重构除去孤立点、填补空洞;②数学形态学闭运算填补表面凹槽,连接狭小断裂;③数学形态学开运算平滑表面,去除毛刺。图 5显示了经过上述数学形态学滤波后得到的结果。

|
| 图 5 数学形态学滤波结果 |
2.5 m分辨率图像可以更加准确地反映道路的位置和形状,5 m分辨率图像在数据分布稀疏区域有更好的增强作用。接着使用数学形态学细化分别处理两幅图像得到栅格道路中心线如图 6所示,显然图 6(b)中道路形状有较大的扭曲,导致交叉口位置有一定的偏移。
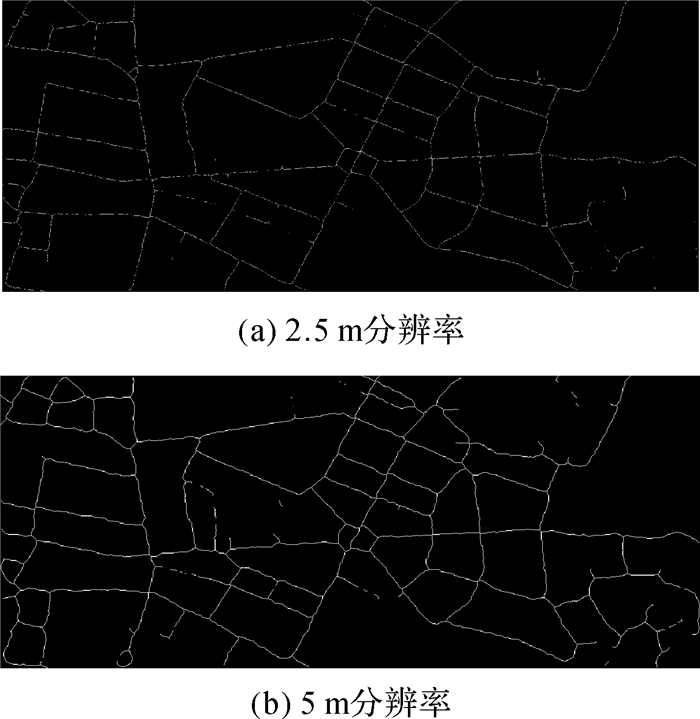
|
| 图 6 数学形态学细化结果 |
提取道路交叉口,从2.5 m分辨率细化图像得到88个,从5 m分辨率细化图得到105个,多提取了17个。融合这两种分辨率图像中提取的交叉口,结果如图 7所示,圆点表示从2.5 m分辨率细化图像上提取出的交叉口,方点代表从5 m分辨率细化图像多提取出的17个交叉口。

|
| 图 7 道路中心线交叉口提取结果 |
由于5 m分辨率的细化图像道路偏移较大,笔者选择2.5 m分辨率细化图像矢量化并经Douglas-Peucker算法化简得到矢量道路中心线,结果如图 8所示。

|
| 图 8 Douglas-Peucker算法化简矢量道路中心线 |
观察试验结果可知,本文道路交叉口提取结果较为准确,但仍存在少许未提取出的道路交叉口,它们往往位于数据采集较少的区域。而本文提取出的道路中心线可以较为准确地体现实际道路的位置、形状和拓扑结构,但在部分区域也出现道路未提取的问题。
5 结语本文面向大量低频低精度GPS轨迹数据提出了一种基于数学形态学的多分辨率图像道路提取方法。该方法在一定程度上克服了低频轨迹数据采样间隔不固定、定位精度低、噪声点多、数据分布不均等缺点,提取出较为准确的道路交叉口和中心线。本文研究成果在导航系统、智能交通系统中有一定的应用价值,下一步将研究如何解决轨迹点分布稀疏区域,数学形态学细化提取道路中心线不全面的问题。
| [1] | SHI W, MIAO Z, DEBAVLE J. An Integrated Method for Urban Main-road Centerline Extraction from Optical Remotely Sensed Imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(6): 3359–3373. DOI:10.1109/TGRS.2013.2272593 |
| [2] | 傅罡. 多源遥感数据的道路提取方法研究[D]. 北京: 清华大学, 2014. |
| [3] | HU X, LI Y, SHAN J, et al. Road Centerline Extraction in Complex Urban Scenes from LiDAR Data Based on Multiple Features[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(11): 7448–7456. DOI:10.1109/TGRS.2014.2312793 |
| [4] | 李卉. 集成LiDAR和遥感影像城市道路提取与三维建模[J]. 测绘学报, 2011, 40(1): 133–133. |
| [5] | LIU X, BIAGIONI J, ERIKSSON J, et al. Mining Large-scale, Sparse GPS Traces for Map Inference:Comparison of Approaches[J]. Proceedings of 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2012, 9(4): 669–677. |
| [6] | KARAGIORGOU S, PFOSER D, SKOUTAS D. Segmentation-based Road Network Construction[C]//Proceedings of the 21st ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. New York: ACM, 2013: 450-453. |
| [7] | STEINER A, LEONHARDT A. Map-generation Algorithm Using Low-frequency Vehicle Position Data[C]//Compendium of Papers of the 90th Annual Meeting of Transportation Research Board. Washington D C: [s. n. ], 2011. |
| [8] | JIANG Y, LI X, LI X, et al. Geometrical Characteristics Extraction and Accuracy Analysis of Road Network Based on Vehicle Trajectory Data[J]. Journal of Geo-Information Science, 2012, 14(2): 165–170. DOI:10.3724/SP.J.1047.2012.00165 |
| [9] | 王振华, 胡翔云, 单杰. 众源GPS浮动车数据中城市道路中心线分级提取的栅格化方法[J]. 测绘通报, 2015(8): 22–24. |
| [10] | FATHI A, KRUMM J. Detecting Road Intersections from GPS Traces[C]//Proceedings of the 6th International Conference on Geographic Information Science. Berlin: Springer-verlag, 2010: 56-69. |
| [11] | 唐炉亮, 刘章, 杨雪, 等. 符合认知规律的时空轨迹融合与路网生成方法[J]. 测绘学报, 2015, 44(11): 1271–1276. DOI:10.11947/j.AGCS.2015.20140591 |
| [12] | GONZALEZ R C, WOODS R E, EDDINS S L. 数字图像处理[M]. 2版. 阮秋琦译. 北京: 电子工业出版社, 2007. |
| [13] | DOUGLAS D, PEUCKER T K. Algorithms for the Deduction of the Number of Points Required to Represent a Digitized Line or Its Caricature[J]. Cartographer, 2011, 10(2): 112–122. |



