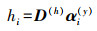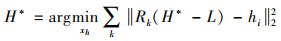2. 地理国情监测国家测绘地理信息局工程中心, 陕西 西安 710054
2. National Geographic Condition Monitoring National Mapping Geographic Information Bureau Engineering Center, Xi'an 710054, China
高分辨率遥感影像在国民经济建设、城市信息提取、精准农业,以及军事测绘等方面都有着广泛的应用前景[1]。作为衡量卫星遥感性能的关键性指标,遥感影像空间分辨率在影像的获取和应用中至关重要[2]。提高遥感影像空间分辨率最直接的方法就是通过硬件改良来提高,但因难度大、成本高且在短时间内较难完成而受到限制。因此,利用超分辨率重建技术来提高遥感影像空间分辨率具有重要的现实意义[1]。超分辨率重建的概念最早由Harris和Goodman分别于1964年和1968年提出[3],是通过对一幅或多幅低分辨率观测图像的处理来重构高分辨率图像的一种技术[4-5]。因具有切实有效、成本低廉的优点,已被广泛应用于视频监控、医疗成像及卫星成像等领域[6]。
就目前的研究成果和应用而言,超分辨率重建方法主要分为基于插值、基于重建及基于学习的方法。其中,基于学习的方法因加入更多先验信息而具有良好的重构结果,已成为目前研究的热点,主要包括基于样本的方法[7]、领域嵌入的方法[8]和稀疏表示的方法[9]。基于稀疏表示的超分辨率重建方法(ScSR)最早由Yang等在2010年提出[10],该方法利用L1正则优化进行稀疏编码,使用不同像素位置加权的字典元素集来表示图像数据,具有较好的重建结果。但这一模型需提前指定字典大小及噪声精度,而在实际应用中,该类参数很难精确估计。非参数Bayesian方法可以很好地解决上述问题[6],该方法能充分利用图像数据的潜在空间结构,利用先验信息由图像数据本身推导得到参数,因其非参数性,减少了人为干涉等因素,提高了模型的自动化程度[11]。且对未知参数进行概率估计而不是点估计,引入了不确定性,避免了不同参数间估计误差的扩大,进一步提高了超分辨率重建结果的质量[12]。本文将非参数Bayesian模型及稀疏表示理论应用于遥感影像处理,提出了一种结合非参数Bayesian字典学习模型及稀疏表示的遥感影像超分辨率重建方法,并针对遥感影像进行了试验。试验数据表明,本文算法在一定程度上提高了重构高分辨率影像的细节精度。
1 稀疏表示原理由于图像本身存在冗余和自关联性,通常情况下,对于图像信号x∈RN,可以由过完备字典D=[d1d2 …dM]∈RN×M(M>N)及向量α=[α1α2 …αM]T∈RM线性表示为
 (1)
(1) 式中,α为稀疏表示系数,为一仅含有少量非零元素的向量。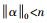
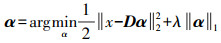 (2)
(2) 字典学习是超分辨率重建的关键步骤。本文使用Beta-Bernoulli process(BP)模型[13-15]进行字典学习,训练得到高、低分辨率特征块所对应的字典D(h)及D(l),其字典元素用dk(h)、dk(l)表示。根据beta过程的一般结构[16],基于BP耦合字典学习的分层模型可表示为
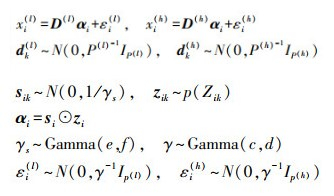 (3)
(3) 式中,xi(h)及xi(l)分别表示高、低分辨率特征块;P(h)及P(l)为对应字典的维数;sik为稀疏权重值;zik为二进制向量,用来记录观测值中被使用的字典元素;p(zik)为变量zik的Beta-Bernoulli process先验,在下一小节进行详述;γs为稀疏权重精度;γ为观测噪声精度;c、d、e、f为超参数;⊙表示两个向量逐元素相乘。
2.2 Beta-Bernoulli process先验对于稀疏权重分量zik,本文使用Beta-Bernoulli process先验来确定其概率分布模型。此先验分布参考IBP(Indian buffet process)的思想[22],其概率建立过程[20]如下:观测值xi服从Bernoulli过程(为一系列独立同分布的贝努力试验),记为xi~BeP(B),其中,B服从贝塔过程,记为B~BP(c0,B0),且B0=N(0,1/β/)。当K趋向于无穷大时,第k个观测值可表示为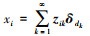
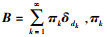
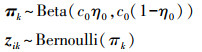 (4)
(4) 式中,超参数c0、η0为标量,k∈1,2,…,K。当k趋向于无穷大时,Beta-Bernoulli近似于IBP/BP。
2.3 基于Beta-Bernoulli process耦合字典的学习利用BP模型进行耦合字典学习,其本质在于利用观测值及各隐变量的先验及条件概率,使用Gibbs迭代抽样形成马尔科夫链,并用其平稳分布来近似字典元素及各参数的后验分布,进而作用于重建阶段的高分辨率影像重构。具体字典学习过程如下:
(1) 抽取N个样本观测值;初始化字典元素及各参数值,迭代次数t初始值为零。
(2) 利用Gibbs抽样进行迭代抽样:将t递增1。
(3) 利用式(5)中各抽样公式分别对字典元素dk(c)及参数sik、zik、πk、γs、γ进行迭代抽样,计算后验概率
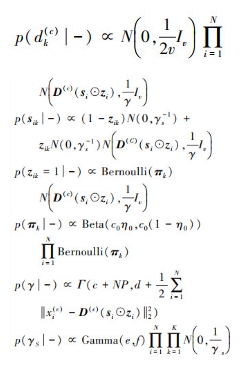 (5)
(5) 式中,I代表v×v的单位矩阵;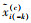
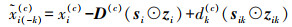 (6)
(6) (4) 当迭代所形成的马尔科夫链为平稳分布时,终止迭代;否则继续。
(5) 输出字典D(h)及D(l)。
3 稀疏表示超分辨率重建由于以低分辨率图像块的细节信息作为特征重建效果较好,本文使用一阶、二阶梯度提取算子对低分辨率影像进行特征提取[10]。具体重建过程即单幅影像超分辨率稀疏重建算法如下:
输入:低分辨率影像L,字典对D(h)及D(l);
输出:高分辨率影像H*。
(1) 从L中随机抽取重叠像素为ω的图像块li,利用一阶二阶梯度提取算子对L进行特征提取,构成低分辨率特征块yi,利用正交匹配追踪算法求解稀疏系数αi(y)
(2) 利用αi(y)及D(h)重建高分辨率影像块
(3) 采用梯度下降算法对步骤(2)中影像块所构成的初始高分辨率影像进行全局约束,得到最终的重建影像
式中,Rk为提取算子。
4 试验及结果分析试验测试数据为3幅资源三号(ZY3)影像及2幅TM5影像。选取100幅高分辨率遥感影像组成训练样本,进行3倍下采样超分辨率重建试验。试验中对应的低分辨率影像由训练样本降采样获得。字典学习阶段,随机抽取105对8×8像素大小的影像块对进行字典学习,块间最大重叠;采用SVD初始化字典元素及各参数值;超参数参考Zhou论文取值为c=d=e=f=10-6、c0=2、η0=0.5;字典大小为2048,前1500次抽样优化模型,后1500次抽样近似字典及各参数的后验分布。重建阶段,迭代次数为40。因人类视觉系统对亮度分量比色度分量更为敏感,故算法均只对亮度通道Y进行基于非参数Bayesian模型的超分辨率重建,而对色度通道(Cb,Cr)仅作双三次插值处理。
试验选用峰值信噪比(PSNR)及ERGAS(erreur relative globale adimensionnelle de synthese)作为定量评价指标,对采用双线性插值方法(Bil.)、双三次插值方法(Bic.)、yang的ScSR方法及本文所提算法得到的超分辨率重建结果进行了比较。图 1、图 2分别为3倍下采样时测试影像ZY3-1、TM5-2在不同算法下的超分辨率重建结果。由图 1、图 2可以看出,Bil.及Bic.插值算法重建的影像整体效果较为模糊,存在过度平滑现象,ScSR重建结果优于插值方法,但本文算法重建图像更为清晰,边缘轮廓及纹理结构更加明显,更好地保留了高频细节信息。

|
| 图 1 影像ZY3_1重建效果比较 |

|
| 图 2 影像TM5_2重建效果比较 |
表 1给出了4种算法下重建影像的PSNR及ERGAS指标值。由表 1可知,本文算法重构影像的PSNR及ERGAS值均优于其他3种算法。综合5幅影像求均值,较Bil.、Bic.及ScSR方法,文中算法的PSNR值分别提高3.29、1.79、0.17 dB;ERGAS值分别降低0.78、0.37、0.02 dB。总体上,本文算法能更好地重构高分辨率遥感影像的细节和纹理特征,证明算法的有效性。
| dB | |||||
| 影像 | 指标 | Bil. | Bic. | ScSR | Proposed |
| ZY3-1 | PSNR | 31.745 3 | 33.727 9 | 35.930 7 | 36.189 2 |
| ERGAS | 2.172 4 | 1.799 | 1.563 8 | 1.537 7 | |
| ZY3-2 | PSNR | 32.605 7 | 35.349 | 37.837 6 | 38.108 1 |
| ERGAS | 1.947 3 | 1.480 2 | 1.235 9 | 1.218 1 | |
| ZY3-3 | PSNR | 30.976 9 | 32.787 7 | 34.933 6 | 35.206 3 |
| ERGAS | 2.623 7 | 2.207 2 | 1.911 1 | 1.877 4 | |
| TM5-1 | PSNR | 23.086 7 | 23.550 5 | 24.188 1 | 24.205 4 |
| ERGAS | 8.437 8 | 8.047 7 | 7.590 1 | 7.57 | |
| TM5-2 | PSNR | 21.018 4 | 21.500 9 | 22.163 7 | 22.177 9 |
| ERGAS | 8.925 2 | 8.503 5 | 7.999 | 7.993 7 | |
本文结合稀疏表示理论,提出了一种基于非参数Bayesian字典学习模型的单幅遥感影像超分辨率重建方法。该方法利用beta先验相关理论建立字典元素及各参数的概率分布模型,采用Gibbs抽样迭代形成马尔科夫链,用其平稳分布来近似字典元素的后验分布,最后作用于重建阶段进行高分辨率影像重构。试验表明,本文算法在视觉效果、峰值信噪比及ERGAS指标3方面均优于其他3种算法,证明了算法的有效性。由于马尔科夫链的平稳分布需通过大量迭代抽样才能获得,对于遥感影像,字典训练所需时间过长,下一步将研究VB等快速近似解求解算法。
| [1] | 刘帅, 朱亚杰, 薛磊. 一种结合稀疏表示和纹理分块的遥感影像超分辨率方法[J]. 武汉大学学报(信息科学版), 2015, 40(5): 578–582. |
| [2] | 徐青. 遥感影像融合与分辨率增强技术[M]. 北京: 科学出版社, 2007: 1-34. |
| [3] | HAMIS J. Diffraction and Resolving Power[J]. Journal of the Optical Society of America(1917-1983), 1964, 54(7): 931–933. DOI:10.1364/JOSA.54.000931 |
| [4] | 钟九生. 基于稀疏表示的光学遥感影像超分辨率重建算法研究[D]. 南京: 南京师范大学, 2013: 1-17. |
| [5] | 沈焕锋, 李平湘, 张良培, 等. 图像超分辨率重建技术与方法综述[J]. 光学技术, 2009, 35(2): 194–199. |
| [6] | POLATKAN G, ZHOU M Y, CARIN L, et al. A Bayesian Nonparametric Approach to Image Super-resolution[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(2): 346–358. DOI:10.1109/TPAMI.2014.2321404 |
| [7] | FREEMAN W T, JONES T R, PASZTOR E C. Example-based Super-resolution[J]. IEEE Computer Graphics and Applications, 2013, 22(2): 56–65. |
| [8] | CHANG H, YEUNG D Y, XIONG Y. Super-resolution through Neighbor Embedding[C]//Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Washington D C: IEEE, 2004: 275-282. |
| [9] | YANG J, WRIGHT J, HUANG T, et al. Image Super-resolution as Sparse Representation of Raw Image Patches[C]//IEEE Conference on Computer Vision and Pattern Recognition. Anchorage: IEEE, 2008: 1-8. |
| [10] | YANG J, WRIGHT J, HUANG T, et al. Image Super-resolu-tion via Sparse Representation[J]. IEEE Transactions on Image Processing, 2010, 19(11): 2861–2873. DOI:10.1109/TIP.2010.2050625 |
| [11] | ZHOU M, CHEN H, PAISLEY J, et al. Non-parametric Bayesian Dictionary Learning for Sparse Image Representa-tions[J]. International Conference on Neural Information Processing Systems: 2295–2303. |
| [12] | RODRIGUEZ A, DUNSON D B. Nonparametric Bayesian Models through Probit Stick-breaking Processes[J]. Bayesian Analysis, 2011, 6(1): 145–178. DOI:10.1214/11-BA605 |
| [13] | KNOWLES D, GHAHRAMANI Z. Infinite Sparse Factor Analysis and Infinite Independent Components Analysis[C]//International Conference on Independent Component Analysis and Signal Separation. [S. l. ]: Springer-Verlag, 2007: 381-388. |
| [14] | PAISLEY J, CARIN L. Nonparametric Factor Analysis with Beta Process Priors[C]//International Conference on Machine Learning. New York: ACM, 2009: 777-784. |
| [15] | ZHOU M, YANG H, SAPIRO G, et al. Dependent Hierarchical Beta Process for Image Interpolation and Denoising[C]//Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics. [S. l. ]: Aistats, 2011: 883-891. |
| [16] | ZHOU M, CHEN H, PAISLEY J, et al. Nonparametric Bayesian Dictionary Learning for Analysis of Noisy and Incomplete Images[J]. IEEE Transactions on Image Processing a Publication of the IEEE Signal Processing Society, 2012, 21(1): 130–144. DOI:10.1109/TIP.2011.2160072 |