2. 贵州大学矿业学院, 贵州 贵阳 550025
2. Mining College, Guizhou University, Guiyang 550025, China
无人机(UAV)是一种动力驱动、无人驾驶、可重复使用的航空器的简称[1],具有机动、灵活、高效、低成本等特点,在国土、水利、农业、林业、城市规划等行业中起到不可估量的作用。与航天遥感影像及传统航空遥感影像相比,无人机影像数据获取简单、空间分辨率高、信息量大,但影像的重叠度高、覆盖区域范围小,单张影像往往难以覆盖目标区域,因此影像镶嵌是无人机影像处理的前期重要工作。而配准与融合是无人机影像拼接的前提,匹配的效果对后续的影像处理具有较大的影响,因此提高特征匹配数及匹配效果很有必要。
图像匹配的本质是在不同的图像上通过算法实现同名点的提取,其中基于图像局部特征的匹配较为常见。David Lowe[2-3]在1999年提出了尺度不变特征转换(SIFT)算法,之后对该算法进行了优化。SIFT算法对旋转、尺度、光照等具有较好的不变性,但SIFT时间、算法复杂度较高,很难达到实时匹配。2006年Herbert Bay等[4]提出了加速特征提取算法(speed up robust features, SURF),该算法是在SIFT算法的基础上改进而来,是对高斯差分的简化,引入积分图像的概念,将卷积运算转化为几个简单的加减运算,降低了算法维度,在加快了程序运行速度的同时具有更好的稳健性。国内外基于SIFT、SURF算法的改进也有大量研究,文献[5-6]通过降维较大程度上减小了算法的时间复杂度,提高了实现效率。杨亮等在克服传统特征匹配算法噪声及图像灰度非线性变换的不足中,通过梯度直方图构造描述符并通过降维来降低时间复杂度[7]。冯亦东等基于传统图像特征信息量少且匹配低的情况,利用SURF算法结合FLANN搜索图像获得了较好的匹配效果[8]。文献[9]通过改进RANSAC算法利用特征点计算出基础矩阵,使匹配效果得到明显提高。同时部分学者将SIFT、SURF算法引用或改进后应用到图像的拼接中[10-12]。基于上述研究,常规算法在无人机遥感影像匹配方面较少,且特征匹配约束条件单一,由于影像局部区域往往只能获取少量或无法获取特征点,这就造成影像的局部区域匹配十分困难。本文基于SURF算法对无人机影像进行特征提取,在快速近视最近邻查找(FLANN)快速搜索算法基础上,结合K最近邻(KNN)[13]筛选掉更多误匹配点,使用单应性矩阵的随机抽样一致性(RANSAC)[14]算法的多重约束得到更好的匹配效果,获得更优的匹配集。
1 影像匹配关键技术 1.1 SURF算法匹配原理及过程(1) SURF是对积分图像进行操作,采用盒子滤波器计算每个像素点的Hessian矩阵行列式,仅需要几次加减运算且运算量与盒子滤波器大小无关,因此能够快速地构成SURF不同尺度的金字塔。积分图像每个像元的值是原图像对应位置所有左上角元素之和,计算公式如下
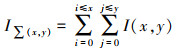 (1)
(1) (2) SURF算法采用对高斯差分近似进行特征点检测,连续函数f(x, y)的二阶微分Hessian矩阵
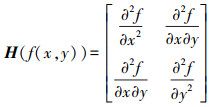 (2)
(2) 同时利用式(3)的值来判断点是否为极值点,在非连续空间上,为了求得矩阵4个元素,因高斯核可以构造出不同的尺度响应图像,SURF算法采用二阶标准高斯核函数对图像卷积,在尺度σ下对应的点(x, y)处对应的Hessian矩阵采用式(4)计算,其行列式的局部最大值可以确定特征点的位置及尺度[15]。
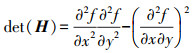 (3)
(3) 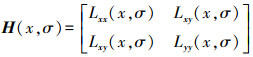 (4)
(4) 式中,Lxx是标准高斯函数G(x, y, σ)的二阶偏导与图像在点(x, y)处卷积后的结果
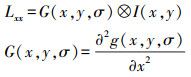 (5)
(5) 同理可得Lxy、Lyy,即可求出Hessian矩阵的值,由于是对原矩阵的近似,因此在计算盒子滤波响应时,需要对模板盒子进行归一化处理。
(3) 构建尺度空间在尺度域及空间域找到极值点,SURF算法采用原图像,大小不变,通过变化模板大小对原图像进行滤波,从而构建出尺度金字塔,把响应图像分成多组,每组由多层组成,各组采用逐渐增大的滤波器尺寸进行处理,其中相邻层间的尺度比例由高斯二阶微分模板决定,一般滤波器尺寸如下
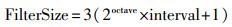 (6)
(6) 式中,octave表示影像所在组;interval表示影像所在层。将每个像素在相邻尺度域及空间邻域内的像素作出比较,如果是极大值或极小值,则将其保留作为候选特征点,同时排除响应值小于Hessian矩阵行列式阈值的特征点。
(4) 由于候选点的空间是离散的,通过拟合准确定位到特征点的位置,每个特征点包含其坐标及其对应的尺度,即H(x, y, σ)。求它在点x处的泰勒展开式,求导得出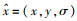
特征匹配一般以欧氏距离为度量,选择固定阈值、最近邻或最近邻距离比率(NNDR)为匹配策略,简单的约束条件一般难以达到满意的效果。针对影像的复杂情况,本文采用多重约束条件使特征点搜索范围更加精确。
1.2.1 同名点极线解算极线约束是一种点对直线的约束而非点对点,它将对应点匹配从整幅图寻找转为在一条直线上寻找对应的点。三维空间中一点P(X, Y, Z),投影到两个不同的平面L1、L2,投影点分别为PL、PR,3个点在三维空间内构成一个平面S,平面S与面L1的交线过PL点,称之为对应于PR的极线。同理S与L2的交线对应PL的极线,即对应于左边图像点的极线在右边图像上,右边图像点的极线与之相反,如图 1所示。
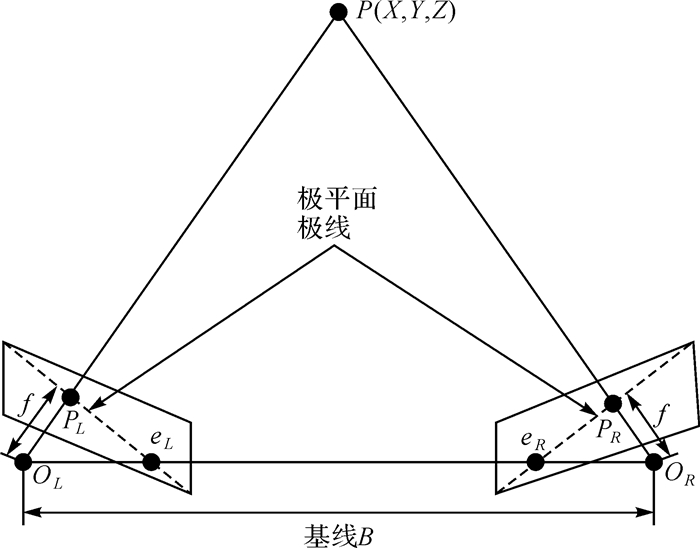
|
| 图 1 极线约束原理 |
由极线原理图可以看出,极线约束就是同一个点在两幅图上的映射,已知左图映射点PL, 则右图映射点PR一定在相对于PL的极线上,这样可以减少影像待匹配的点数量。基础矩阵F将点PL映射到另一个视角中的极线上,假如三维向量x、x′存放相关点,F为一个3阶且秩为2的基础矩阵,则满足
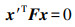 (7)
(7) 在约束匹配的过程中,使用基础矩阵或单应性矩阵的RANSAC算法去除误匹配点对,基本矩阵是秩为2、自由度为7的3×3矩阵。其中
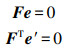 (8)
(8) 假设两幅图之间是透视变换,则单应性矩阵(即透视变换矩阵)每次需要4对匹配点来计算H,然后选出内点个数最多作为最后的结果,其计算距离方法如下
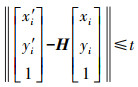 (9)
(9) 矩阵F和H的关系如式(10)所示,但通常由于极线约束估计不准确使得两矩阵的估计存在偏差,使得二者之和不等于零,可以设定阈值来判定矩阵是否准确。
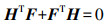 (10)
(10) 采用RANSAC算法在一组包含“外点”的数据集中不断迭代寻找最优参数模型,其实质是寻找一个最佳单应性矩阵H,矩阵大小为3×3,找到最优参数矩阵时满足矩阵的特征点最多,由于矩阵H有8个未知参数,因此需要至少包含4组匹配点对
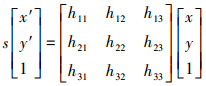 (11)
(11) 式中,(x, y)表示目标图像角点位置;(x′, y′)为场景图像角点位置;s为尺度参数。该算法随机从匹配数据集中抽取4对点并要求相互之间不共线,计算出单应性矩阵H,利用该模型去检测所有数据,如果该模型最优,则应满足该模型的点个数与投影误差(即代价函数)最小
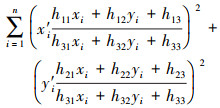 (12)
(12) RANSAC参数估计内涵:给定N个数据点组成集合W,假设集合W中大多数点可以通过模型产生,且最少通过n个点(n<N)可以拟合出模型参数。本文参数估计最大迭代数为100,最多的点数为1000,同时本文模型包括基础矩阵和单应性矩阵。
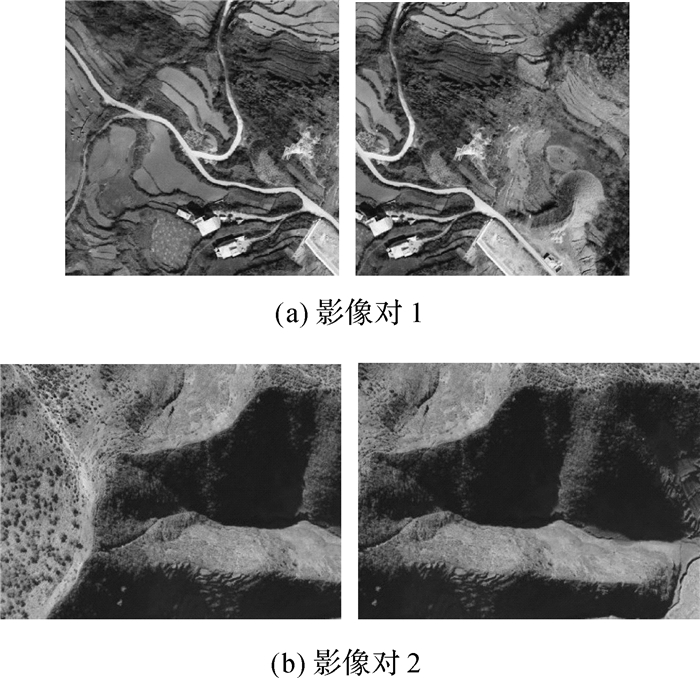
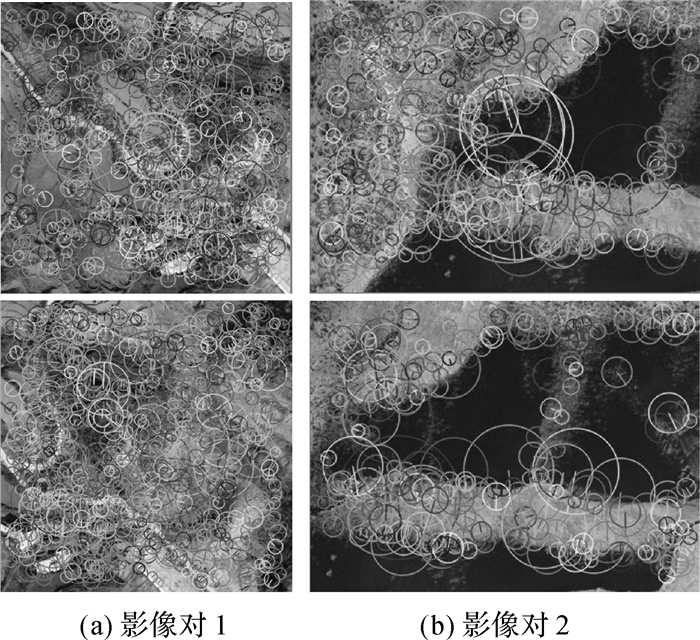
2 试验过程及分析本文基于SURF算法,首先进行无人机影像特征点提取,引入多重特征约束条件控制约束力度,逐步过滤掉错误匹配的特征点使匹配效果更佳。利用3种算法对分辨率为380×380、400×300的两组数据(山地)进行前2次试验之后改进算法实现试验3,并分析匹配效果、运行时间及匹配精度。本次试验运行环境为Inter(R) Xeon(R) CPU E5-1607 0@3.00 GHz,运行内存为8 GB的工作站。基于VS2013的OpenCV2.4.10图像处理视觉库,Windows 7系统作为开发平台,无人机影像部分参数见表 1。试验数据如图 2所示,可以看出影像对1左右影像变形较大, 影像对2地形起伏大。图 3为两组影像对的特征点检测,其中影像对1特征点数为877、936,影像对1特征检测数为490、313。
|
| 图 2 影像对 |
|
| 图 3 两组影像对SURF特征点检测 |
试验1:基于SURF算法结合FLANN快速搜索的特征匹配。图 4为两组影像对匹配结果,其中影像对1匹配数为187,耗时1 844.76 ms,影像对2匹配数为59,耗时970.722 ms。

|
| 图 4 影像对SURF+FLANN匹配效果 |
试验2:基于基础矩阵的极线约束特征匹配,并用RANSAC方法计算出基本矩阵,在挖掘更多特征点的同时通过极线约束筛选掉错误特征点,使得内点更纯净。该算法实现影像对1耗时2 472.21 ms, 特征匹配对494,影像对2耗时1 274.34 ms, 特征匹配对212,匹配效果如图 5所示。从图中可以看出引入极线约束的特征匹配在增加特征点的同时提高了匹配量,匹配效果得到明显提高,同时图中存在少量的误匹配。

|
| 图 5 两组影像SURF+FLANN+基础矩阵匹配效果 |
试验3:使用单应性矩阵的方法去除误匹配点对更加严格,得到的结果更加精确,试验基于SURF算法,结合FLANN快速搜索并用KNN算法筛选匹配点,使用单应性矩阵的RANSAC算法去除误匹配点后,得到了更好的匹配效果,如图 6所示,匹配更精确。改进后的算法影像对1耗时2 307.7 ms,匹配上470对,影像对2耗时1 344.13 ms,匹配上194对。
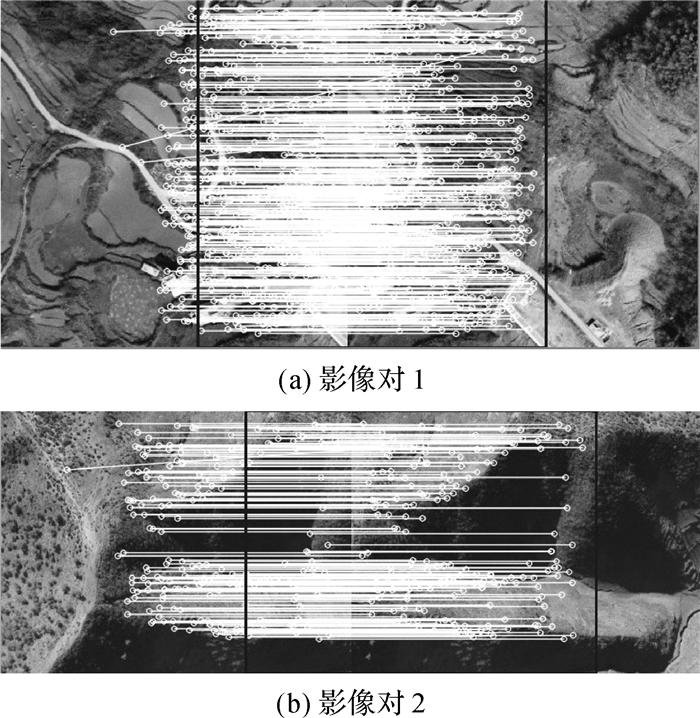
|
| 图 6 改进后两组影像匹配效果 |
试验首先基于SURF算法对两组无人机影像进行关键点检测,结合FLANN快速搜索算法做出匹配,匹配效果较好,但特征点较少。通过改进算法在FLANN基础上结合KNN筛选掉更多误匹配点,使用单应性矩阵的RANSAC算法得到更好的匹配效果。3组试验在两组数据中匹配对数、耗时及正确率见表 2。
| 影像对 | 试验1 | 试验2 | 试验3 | ||||||||
| 匹配对数 | 时间/ms | 正确率/(%) | 匹配对数 | 时间/ms | 正确率/(%) | 匹配对数 | 时间/ms | 正确率/(%) | |||
| 1 | 187 | 1 844.76 | 89.8 | 494 | 2 472.21 | 93.1 | 470 | 2 307.7 | 95.1 | ||
| 2 | 59 | 970.722 | 88.1 | 212 | 1 274.34 | 90.1 | 194 | 1 344.13 | 93.8 | ||
从表中可以看出引入极线约束的匹配数是基于SURF和FLANN算法的匹配量的约3~5倍,但极线约束后的匹配同时还存在少量的极线交叉导致匹配错误。3组试验匹配率相差不大,影像对1匹配率分别为89.8%、93.1%、95.1%,影像对2匹配率分别为88.1%、90.1%、93.8%,但两组影像在试验1中能够匹配到的特征点太少,因此利用该算法一般难以满足影像间的匹配,特别是地形起伏较大区域,如影像对2在试验1中局部区域甚至没有特征点。由于单应性矩阵比基础矩阵更严格,造成匹配量上基础矩阵稍低,但精度要比基于基础矩阵的特征匹配高。在耗时上,由于试验1算法复杂度相对后两种算法要低,考虑的参数要少,因此两组影像在试验1中速度较快,而试验2、试验3两种算法时间复杂度相差不大,改进后的算法相对于前两个试验在耗时得到控制的同时而获取了更多精度较高的匹配集。
3 结语本文针对无人机影像受拍摄条件影响或区域环境复杂造成的匹配效果不佳,局部区域没有特征点造成的匹配难度大,为了避免传统约束条件单一的不足而在SURF算法的基础上基于FLANN快速搜索结合KNN算法并引入单应性矩阵,同时与基于基础矩阵的极线约束条件及常规的算法作了对比。试验证明,基于多重约束条件的特征匹配获得了较好的匹配效果,在获取大量特征点的同时获得了更多优质匹配集,该算法适合无人机影像的匹配。
| [1] | 姬渊, 秦志远, 王秉杰, 等. 小型无人机遥感平台在摄影测量中的应用研究[J]. 测绘科技装备, 2008, 10(1): 46–48. |
| [2] | LOWE D G. Object Recognition from Local Scale-invariant Features[C]//Proceedings of the 7th IEEE International Conference on Computer Vision. Piscataway, NJ: IEEE, 1999: 1150-1157. |
| [3] | LOWE D G. Distinctive Image Features form Scale-invariant Keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91–110. DOI:10.1023/B:VISI.0000029664.99615.94 |
| [4] | BAY H, TUYTELAARS T, GOOL L V. SURF: Speeded Up Robust Features[C]//Proceedings of European Conference on Computer Vision. Graz, Austria: [s. n. ], 2006: 404-407. |
| [5] | YAN K, SUKTHANKAR R. PCA-SIFT: A More Distinctive Representation for Local Image Descriptors[C]//Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2004: 511-517. |
| [6] | 张春美, 龚志辉, 孙雷. 改进SIFT特征在图像匹配中的应用[J]. 计算机工程与应用, 2008, 44(2): 95–97. |
| [7] | 杨亮, 郭新宇, 赵春江, 等. 一种基于SIFT描述子的特征匹配新算法[J]. 微计算机信息, 2009, 25(28): 135–137. DOI:10.3969/j.issn.2095-6835.2009.28.055 |
| [8] | 冯亦东, 孙跃. 基于SURF特征提取和FLANN搜索的图像匹配算法[J]. 图学学报, 2015, 36(4): 650–654. |
| [9] | 甄艳, 刘学军, 王美珍. 一种改进RANSAC的基础矩阵估计方法[J]. 测绘通报, 2014(4): 39–43. |
| [10] | 胡同喜, 牛雪峰, 谭洋, 等. 基于SURF算法的无人机遥感影像拼接技术[J]. 测绘通报, 2015(1): 55–58, 74. |
| [11] | 何敬, 李永树, 鲁恒, 等. 基于SIFT特征点的无人机影像拼接方法研究[J]. 光电工程, 2011, 38(2): 122–126. |
| [12] | 许超, 聂诗良. 基于SURF和改进渐入渐出法的图像拼接算法[J]. 数字技术与应用, 2016(12): 133–136. |
| [13] | ALTMAN N S. An Introduction to Kernel and Nearest-neighbor Nonparametric Regression[J]. American Statistician, 1992, 46(3): 175–185. |
| [14] | FISCHLER M A, BOLLES R C. Random Sample Consensus:A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography[J]. ACM Graphics and Image Processing(S0001-0782), 1981, 24(6): 381–395. |
| [15] | 时磊, 谢晓方, 乔勇军. 基于SURF算法和OpenCV的人脸特征检测技术研究[J]. 计算机与数字工程, 2010, 38(2): 124–126. |


