超短基线(ultra-short baseline,USBL)定位系统是一种常用的水下声学定位设备[1-4]。常规的USBL系统通过测量各通道间的相位差或时延差估算目标方位,再利用应答或同步方式测量目标的斜距,进而确定目标的位置。
USBL系统的设计是水下声学定位技术中的一项关键技术,平面阵可以对整个空间或以阵列所在平面为界的半空间中的目标进行定位,在许多情况下都可以达到系统的设计要求。文献[5-6]研究了平面阵的定位原理,并进行了详细的误差分析。文献[7-10]提出了平面八元阵定位原理,通过增加阵元个数有效地解决了USBL系统中存在的相位差模糊问题。文献[11-12]介绍了一种三维立体USBL系统接收阵列的设计。文献[13]在六元对称阵的基础上,给出了若干种USBL系统定位算法。由于基阵孔径小,且复杂的水下环境容易导致信号的相位产生起伏,常规USBL系统定位精度不高。为了满足远距离定位要求,必须对常规USBL系统进行改进。
本文在常用的平面阵定位原理及定位方程的基础上提出一种提高USBL系统定位精度的方法。以平面五元十字阵为例,系统仅需要测量一次时延差值,即可通过基本的平面阵独立地对目标进行定位,随后将这些独立的定位结果进行有效的数据融合,进而得到最终的定位结果。仿真试验表明, 该方法可以有效地提高低信噪比情况下USBL系统的定位精度和可靠性。
1 USBL系统的基本原理平面五元十字阵的定位原理如图 1所示。在图 1中,平面五元十字阵由两条正交的线阵S1-S0-S3和S2-S0-S4构成。阵元间距为D,以基阵中心S0为坐标原点O建立直角坐标系,5个阵元的坐标分别为S0(0, 0, 0)、S1(D, 0, 0)、S2(0, D, 0)、S3(-D, 0, 0)、S4(0,-D, 0)。假设目标位于T处,T′为T在xoy平面上的投影。T的直角坐标为(x, y, z),球坐标为(R, φ, θ),R、φ、θ分别为目标到基阵中心的斜距、方位角和俯仰角。其中,斜距R=Δt·c,Δt为信号从目标到阵元S0的传播时间,c为声速。
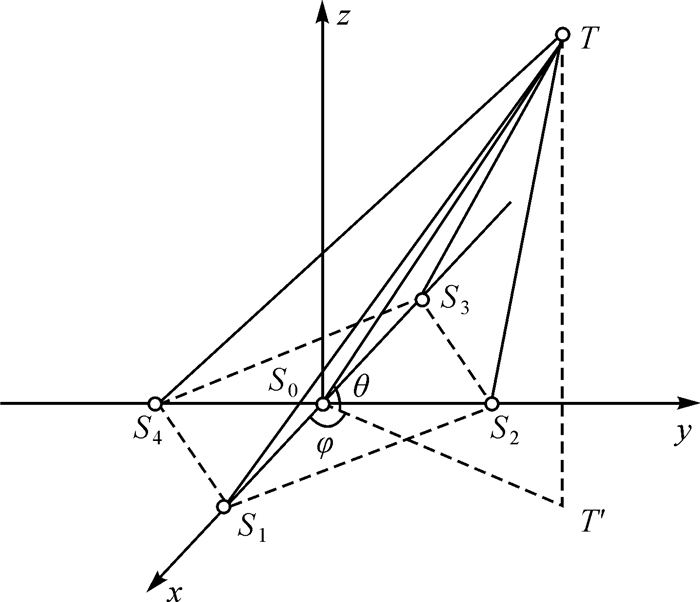
|
| 图 1 平面五元十字阵定位原理 |
为了确定目标方位,USBL系统至少需要由3个基元构成[14],令声信号由目标传播到阵元Si的时延为τi,且τij=τj-τi,则三元阵可以通过以下公式计算目标的方位[15]
 (1)
(1) 十字正交阵与三元阵定位原理相同。图 1所示的五元十字阵中包括8个正交的三元阵:USBL012、USBL023、USBL034、USBL041、USBL123、USBL234、USBL341、USBL412(下标的数字为所包含阵元的标识),以及1个十字正交阵USBL1234。
在图 1中,S1、S2、S3、S4这4个阵元构成平面四元十字阵,本文中标识为USBL4。平面四元十字阵的定位方程为[5]
 (2)
(2) 平面五元十字阵(本文中标识为USBL5)是在平面四元十字阵的基础上在基阵中心增加了1个阵元S0,其定位方程为[6]
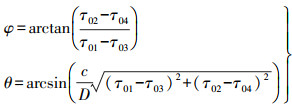 (3)
(3) 在利用到达时延差(time difference of arrival,TDOA)测量值对目标进行定向的USBL系统中,系统定位精度与传感器和目标之间的相对几何位置关系有关[16],不同的阵型对目标进行定位的精度也存在差别。为此,本文通过下面步骤来对各基本阵型的初始定位坐标进行数据融合,以达到提高USBL系统定位精度的目的。
(1) 计算每个定位坐标到其余坐标的欧氏距离之和为
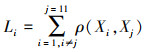 (4)
(4) 式中,Xi(xi, yi, zi)、Xj(xj, yj, zj)为三维定位坐标;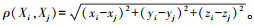
(2) 选择到其余点距离和最小的那个坐标点作为初始定位点的中心
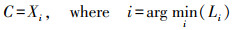 (5)
(5) (3) 重新计算每个节点到中心C的欧氏距离Lj=ρ(C, Xj)(j=1, …, 11;j≠i);并计算平均距离L=Lj;若Xj满足下式,则将Xj视为异常定位点,将其排除,其余的初始定位点被视为是有效的。
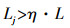 (6)
(6) 式中,η为经验参数。其值的大小决定着参与数据融合的有效点的个数。
(4) 对有效点的坐标运用LS(Least Square)方法,得到最终的定位结果。
3 仿真试验仿真试验采用同步信标作为定位目标,目标与USBL系统之间的斜距为1 km。背景干扰为加性高斯白噪声,USBL系统接收阵尺寸为D=0.10 m。同步信标发送时长为5 ms,中心频率fc=13.5 kHz,带宽B=3 kHz的线性调频信号(linear frequency modulation,LFM),USBL系统采样频率fs=100 kHz。声信号以c=1500 m/s的速度进行直线传播,忽略声线弯曲及多途效应的影响。时延信息根据目标与各阵元声程差反向推导添加到各阵元接收信号中。系统定位误差主要来源于时延估计误差。选择三元阵USBL012,平面四元阵USBL4和平面五元阵USBL5为参照系统,使用本文方法的定位系统被标识为USBLall。式(6)中的经验参数η值取为2。仿真过程中,在给定俯仰角的情况下通过以1°为步长改变目标与USBL系统之间的方位角来改变目标的坐标,每种基本阵型可以计算得到360个定位结果。令第i次测得的定位结果由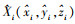
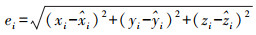 (7)
(7) 通过式(8)来计算定位距离误差的平均值和标准差,并对比各系统的定位精度
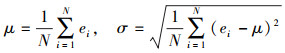 (8)
(8) 式中,N=360,为测试的次数。
改变接收信号的信噪比,测试USBL系统在不同信噪比条件下的距离定位精度。接收信号信噪比范围设置为[-10 dB,20 dB],目标与USBL系统之间的俯仰角取为θ=40°。测试结果如图 2所示。

|
| 图 2 各阵型USBL系统定位精度与信噪比的关系 |
从图 2可以看出,在信噪比较高的情况下,各种基本阵型都具备较好的定位性能,但是在信噪比较低的情况下,各种基本阵型均容易出现较大的定位误差。本文方法综合了各基本阵型的定位结果,选择了其中较可靠的定位结果进行融合,使得系统总体的定位性能随着信噪比的降低而下降得更为缓慢。试验结果说明, 本文方法可以有效地提高低信噪比情况下USBL系统定位的精度和可靠性。
通过测量USBL系统在给定俯仰角情况下的定位精度来测试各阵型定位方法与俯仰角之间的关系,信噪比固定为-5 dB。试验结果如图 3所示。

|
| 图 3 各阵型USBL系统定位精度与俯仰角的关系 |
由图 3可以看出,与另外3个阵型的USBL系统相比,USBLall系统在目标位于不同俯仰角的情况中,距离定位误差的平均值和标准差都相对较低,说明本文方法可以提高目标位于不同俯仰角情况下USBL系统的可靠性和精度。
使用本文方法对目标进行定位,通过改变经验参数η的取值来测试其对USBL系统定位精度的影响。试验中信噪比固定为-5 dB,目标与USBL系统之间的俯仰角θ=40°。通过以1°为步长改变目标方位角来改变目标的真实坐标,令第i次定位过程中有εi个初始定位点被判断为异常点。通过式(9)计算异常点的平均数
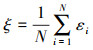 (9)
(9) 式中,N=360为测试的次数。同时,试验还通过式(7)和式(8)计算了不同经验参数情况下定位距离误差的平均值和标准差。试验结果如图 4所示。
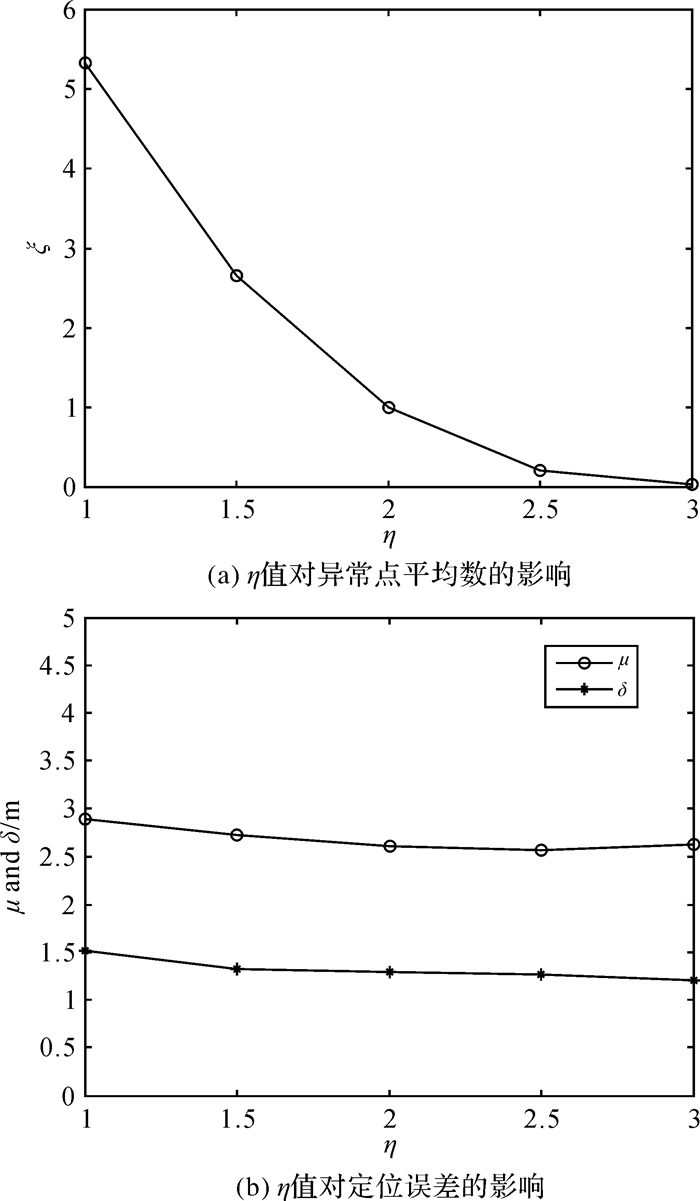
|
| 图 4 η值对距离定位误差的影响 |
由图 4可以看出,η的不同取值对基本阵型定位结果中被视为异常点的个数有较大影响,但是其对最终数据融合后的USBL系统定位结果影响不大。不同的η值所得到的距离定位误差,其平均值和标准差都保持相对稳定。
4 结语本文提出了一种利用数据融合改进USBL系统定位精度的方法。系统仅需要测量一次信号到达各阵元的时延,通过综合各种阵型定位结果,即可达到提高USBL系统可靠性和定位精度的目的。通过仿真试验证明了本文提出的方法在不同信噪比和目标处于不同俯仰角的情况下均能提高USBL系统的定位精度。
| [1] | REIS J, MORGADO M, BATISTA P, et al. Design and Experimental Validation of a USBL Underwater Acoustic Positioning System[J]. Sensors, 2016, 16(9): 1491–1513. DOI:10.3390/s16091491 |
| [2] | CONTI F K P, BJERKE E, BROWN G. Acoustic Search of Aircraft CVR/FDR in the Ocean Floor Using USBL/SSBL Hydroacoustic Positioning Systems: Results Achieved in Real Environment Operational Tests[C]//Acoustics in Underwater Geosciences Symposium. Rio de Janeiro: IEEE, 2015: 1-6. |
| [3] | CAITI A, CORATO F D, FENUCCI D, et al. Experimental Results with a Mixed USBL/LBL System for AUV Navigation[C]//Underwater Communications and Networking. Sestri Levante: IEEE, 2015: 1-4. |
| [4] | CORATO F D, FENUCCI D, CAITI A, et al. Toward Underwater Acoustic-based Simultaneous Localization and Mapping: Experimental Results with the Typhoon AUV at CommsNet13 Sea Trial[C]//Oceans. St John's: IEEE, 2014: 1-7. |
| [5] | 贾云得, 冷树林, 刘万春, 等. 一种简易被动声直升机定位系统[J]. 北京理工大学学报, 2000, 20(3): 338–342. |
| [6] | 陈华伟, 赵俊渭, 郭业才. 五元十字阵被动声定位算法及其性能研究[J]. 探测与控制学报, 2003, 25(4): 11–16. |
| [7] | 喻敏, 惠俊英, 冯海泓, 等. 超短基线系统定位精度改进方法[J]. 海洋工程, 2006, 24(1): 86–91. |
| [8] | 喻敏, 惠俊英, 孙大军. 超短基线基阵基元相移差的测量[J]. 应用声学, 2006, 25(4): 229–233. DOI:10.11684/j.issn.1000-310X.2006.04.009 |
| [9] | 李想, 张殿伦, 孙大军, 等. 高精度超短基线定位系统的实现[J]. 计算机工程与应用, 2007, 43(24): 176–178. DOI:10.3321/j.issn:1002-8331.2007.24.050 |
| [10] | 赵安邦, 何文翔, 董海防, 等. 声速分布深海超短基线定位算法[J]. 系统仿真学报, 2009, 21(15): 4763–4767. |
| [11] | ARKHIPOV M. An Approach to Using Basic Three-element Arrays in Tetrahedral-based USBL Systems[C]//Oceans. San Diego: IEEE, 2013: 1-8. |
| [12] | ARKHIPOV M. Designing a USBL System Based on a Square Pyramid Array with a Complete Set of Three-element Arrays[C]//Oceans. [S. l. ]: IEEE, 2012: 1-9. |
| [13] | ZHONG F, ZHOU W. Optimal Method for USBL Underwater Acoustic Positioning by Combining TDOA and TOA[C]//ACM International Conference on Underwater Networks & Systems. New York: ACM, 2016: 45. |
| [14] | VICKERY K. Acoustic Positioning Systems: A Practical Overview of Current Systems[C]//The Workshop on Auto-nomous Underwater Vehicles. Cambridge: IEEE, 1998: 5-17. |
| [15] | ZHANG L. An Design Method of Underwater Positioning System Based on USBL[J]. Applied Mechanics & Materials, 2014(644-650): 968–972. |
| [16] | BISHOP A N, FIDAN B, ANDERSON B, et al. Optimality Analysis of Sensor-target Localization Geometries[J]. Automatica, 2010, 46(3): 479–492. DOI:10.1016/j.automatica.2009.12.003 |


