2. 首都师范大学三维数据获取与应用重点实验室, 北京 100048
2. Key Lab of 3D Information Acquisition and Application, Capital Normal University, Beijing 100048, China
近年来,伴随着城市的快速扩张,地铁和高铁已经成为人们出行的主要交通工具之一,且建设规模正在不断扩大,而隧道工程在其中发挥着重要的作用。因此,对地铁和高铁隧道进行精准、快速、自动化的形变监测对于确保地下列车的安全运营显得十分必要。传统的隧道形变监测方法(如全站仪、收敛计等)[1]多是通过在现场测量隧道的横断面来分析其形变,虽然监测精度较高,但效率低。三维激光扫描技术由于获取数据速度快、点密度大、精度高、使用简单方便等优点[2],在隧道监测方面的应用前景较为广阔。因此,如何利用大量的隧道点云数据对隧道的形变进行精准的分析成为当前的研究热点。国内外众多学者均对此进行了研究和探索,多是通过从点云数据中提取隧道的横断面来分析其形变,而对于横断面提取方法的研究则主要集中在如何使断面更加精确地与隧道正交的问题上。具体主要分为以下几类:①旋转隧道点云数据使其走向与某一坐标轴基本平行,并利用该坐标轴切割断面[3]。②将隧道点云投影到水平面并转换成二值图像,利用图像提取中轴线在水平面的投影曲线来切割断面[4]。以上两种方法由于只考虑了隧道在水平面的姿态,均需通过后期的断面调整算法来提高断面的提取精度,以使其与隧道完全正交。③直接以设计中轴线为基础进行横断面的截取[5]。由于设计数据的获取比较困难,导致该方法的应用具有一定的局限性。④对隧道点云向两个平面进行投影,然后采用数学方法提取空间中轴线并切割断面[6]。该方法综合考虑了隧道在水平和竖直方向的姿态,以此为基础切割断面,提高了断面的准确度。此外,纵观国内外的研究现状可知,当前的研究方法均是基于站式激光扫描技术所获取的点云数据来进行隧道的形变分析。而移动激光扫描技术[7]相比传统的站式激光扫描技术获取数据速度更快,能够在短时间内一次完成整个隧道的测量工作,省去了后期的拼站过程,更加适用于隧道内运营时间有限、工况条件差等特殊的条件。
本文提出将基于移动激光扫描技术获取的点云数据研究隧道形变分析的方法,对现有的方法进行一定的改进。首先,将隧道点云数据向水平面投影并计算中轴线在该平面上的投影点集,以该点集为基础通过搜索高低点的方法获取最终的空间中轴线;其次,以中轴线为基础采用投影法构建断面点集,在此过程中通过k近邻法对隧道点云进行分块,以提高断面点集获取的速度;此外,提出一种迭代椭圆拟合去噪方法,在去除断面噪声的同时拟合出断面线;最终将该方法应用在实际的隧道点云自动提取横断面并根据横断面分析隧道的形变。
1 隧道横断面的自动提取方法 1.1 隧道中轴线提取图 1所示为移动激光扫描技术获取的隧道点云在WGS-84绝对坐标系下的分布,其中Y轴与Z轴、X轴垂直构成右手坐标系,因此只需计算出隧道在XOY平面和YOZ平面的方向曲线(即中轴线)便可确定隧道在水平和竖直方向的姿态和走势;进而通过计算中轴线在各断面截取点处的切向量,计算出与隧道处处垂直的横断面,以此来分析隧道的形变[6]。由于空间曲线的计算比较复杂,当前比较常用的方法是通过降维,即将三维点云数据向二维平面进行投影或将其转换成二维图像来提取中轴线。

|
| 图 1 绝对坐标系下的隧道点云数据 |
本文将中轴线的提取分为两部分,首先计算出中轴线在XOY面的投影曲线,然后以此为基础计算出能够表达中轴线在竖直方向走势的点集,最终得到中轴线在YOZ面的投影曲线。该方法基于绝对坐标系下的隧道点云数据直接提取中轴线,省去了以往方法中[6]需要先将隧道点云数据旋转到与某一坐标轴平行再提取中轴线的过程,明显减小了计算量,具体步骤如下:
(1) 将隧道的三维点云数据向XOY面进行投影,通过边界检测算法检测出投影后的边界点集,并采用二次曲线方程分别拟合两组边界点集。其中曲线方程的参数估计采用抗噪效果较好的随机抽样一致性算法[8],最终拟合出两条边界曲线。
(2) 在其中的一条边界曲线上等间隔选择点集U1,并计算点集中每一点在其法线方向上与另一条边界曲线的交点,组成点集U2,由点集U1和U2中的对应点内插得到中轴线在XOY面上的投影点集UXOY,如图 2所示,深灰色的点即为点集UXOY。
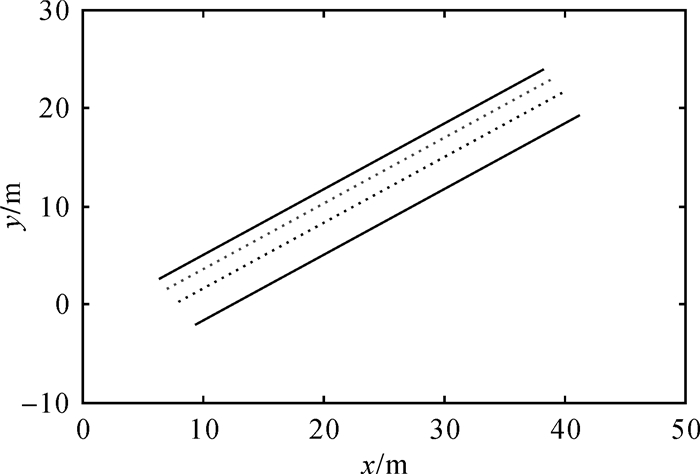
|
| 图 2 中轴线在XOY面的投影点集 |
(3) 利用移动激光扫描设备进行数据采集存在设备遮挡问题,使得隧道下方通常会存在部分点云的缺失。为了方便下一步的计算,需要将点集UXOY沿着其法向平移一定距离l(轨距/2 < l < 隧道内径/2),以保证UXOY对应的隧道下方存在点云数据,如图 2所示,浅灰色的点集为黑色点集UXOY向其法方向移动之后的数据。
(4) 对平移后的点集Uxoy中的每一点在垂直于XOY面的方向上搜索最高点和最低点,组成点集P3和P4,如图 3所示。

|
| 图 3 隧道的高低点 |
虽然点云密度较大,但并不能保证每一点处都能搜索到对应的高低点,此时选择距离搜索方向最近的点作为相应的高低点。获取点集P3和P4之后将其投影到YOZ面上并重复步骤(3)、(4),计算中轴线在YOZ面的投影点集UYOZ。最后采用最小二乘法利用式(1)对点集Uxoy和Uyoz进行曲线拟合,得到隧道的空间中轴线
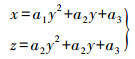 (1)
(1) 计算断面的缓冲区实质上是对隧道点云进行分块的过程,其目的是提高断面点集获取的速度。首先根据待截取的断面的数量在中轴线上选择n个断面截取点并将点云数据和断面截取点同时投影在XOY平面上,然后搜索每一个断面截取点在其法线方向上分别与两边界线的交点,组成点集N1和N2。其次,在点集N1和N2之间每隔距离ε选择一定数量的点,并采用k近邻法[9]搜索距离每个点最近的k个点(k的选取应该保证缓冲区范围内的最小半径大于ε),构成每个断面的缓冲区。图 4为断面缓冲区的构建过程。
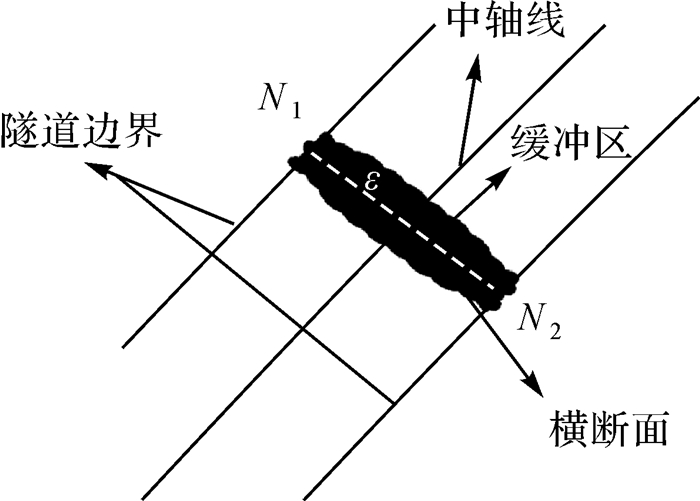
|
| 图 4 断面缓冲区的构建 |
隧道的横断面是与隧道中轴线处处垂直的平面。由于断面的截取点位于中轴线上,因此根据式(2)可以计算每一个断面截取点处的切向量(1,kp,kpp),即为该截取点处的横断面的法向量,从而得出第i个断面截取点处垂直于中轴线的法平面的方程为
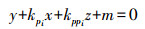 (2)
(2) 为了提高断面点的密度,进而更加精确地确定断面每个角度位置上的形变情况,可参考文献[10]中的方法,将每个缓冲区内到对应法平面距离小于δ的点投影在法平面上(δ的值等于点云数据获取时的绝对精度)。
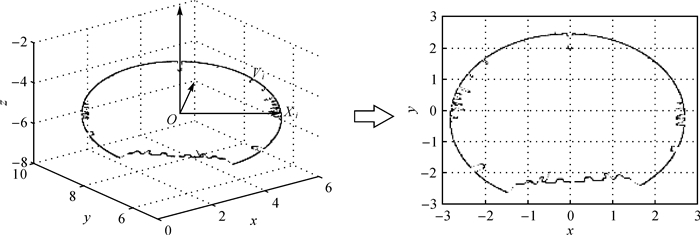
1.3 断面点集的去噪与断面线的拟合 1.3.1 断面坐标的转换通过建立各断面的局部坐标系,将断面点的三维坐标转换成二维坐标,进而采用椭圆模型来拟合隧道断面线。如图 5所示,第i个断面的局部坐标系的原点Oi为该断面的截取点,Xi轴平行于XOY平面且垂直于该断面的法向量Vi,Yi轴过原点Oi垂直于XiOiVi平面。断面点在Oi-XiYiVi坐标系下的坐标通过式(3)和式(4)计算
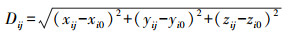 (3)
(3) 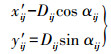 (4)
(4)
|
| 图 5 断面局部坐标系的建立 |
式中,Dij为第i个断面点集中第j个点(xij,yij,zij)到该断面对应的截取点Oi(xiO,yiO,ziO)的距离;αij为第i个断面点集中的第j个点与断面截取点Oi的连线到X坐标轴正向的夹角;(x′ij,y′ij)为第i个断面点集中的第j个点转换之后的平面坐标。
1.3.2 断面线拟合与噪声去除传统的车载点云的噪声去除方法一般是对机载点云的去噪方法进行相应的改进[11]。隧道是一个封闭的空间,不能直接应用或改进机载点云的去噪方法,且经过变形之后的隧道断面可以认为是一个接近标准圆的椭圆[12]。因此本文提出一种迭代椭圆拟合去噪的方法进行断面点噪声的去除,椭圆拟合时的参数估计采用随机抽样一致性算法。首先对含有噪声的隧道断面进行初始的椭圆拟合,计算出椭圆的初始参数(包括椭圆方程的系数、圆心坐标、长短半轴等),然后求算断面点到椭圆的最短距离di,进而组成距离点集d{d1, d2, …, dn},并根据式(5)和式(6)计算点集d的均值dmean和标准差σ
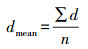 (5)
(5) 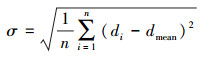 (6)
(6) 规定当|di-dmean|>2σ时,断面点为噪声,经过不断迭代,最终去除了非隧道壁上的点,并得到了断面线的拟合结果。试验表明,在迭代去噪过程中,当迭代次数为10时,能够有效去除断面的噪声且很好地保留了断面点的信息。
2 数据获取与方法验证本文选择的试验区为上海某段圆形盾构隧道,长约38 m,起点里程为K27+280,隧道衬砌内径为5.5 m,衬砌为预制钢筋混凝土管片。通过自主研发的手推式隧道检测小车采集该段隧道的点云数据,点间距小于2 cm,获取数据时的精度为2 mm,共采集到10 356 374个点,如图 1所示。由于本文通过移动激光扫描技术获取点云数据,省去了多站扫描、数据拼接等数据处理过程,在对原始数据进行解算之后可以直接用于后期的数据处理。
为了验证方法的有效性,在里程K27+300处采用全站仪进行断面测量,测量过程中保证所有的断面点在同一平面上,最终共获取17个断面点。首先采用本文方法处理点云数据,得到该里程处的断面并拟合椭圆断面线,椭圆长半轴为2.762 m,短半轴为2.730 m,扁率为1.16%;其次,对全站仪获取的数据建立断面局部坐标系并拟合断面线,椭圆长半轴为2.758 m,短半轴为2.731 m,扁率为0.99%。由此可知,两种测量手段获取的断面线长半轴和短半轴的差值分别为4和1 mm,即横向和纵向最大形变差值。本文将全站仪测量的断面作为参考基准,认为其不存在误差,同时将全站仪进行隧道收敛变形监测的中误差(2.4 mm)作为衡量指标。因此,采用本文中的方法计算的断面与全站仪测量的断面的横向和纵向最大变形差值均小于2倍的中误差(4.8 mm),验证了方法的可行性。
3 应用实例与形变分析 3.1 断面点集的计算首先采用前文方法进行隧道中轴线的提取,最终得到的中轴线的方程如下
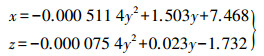 (7)
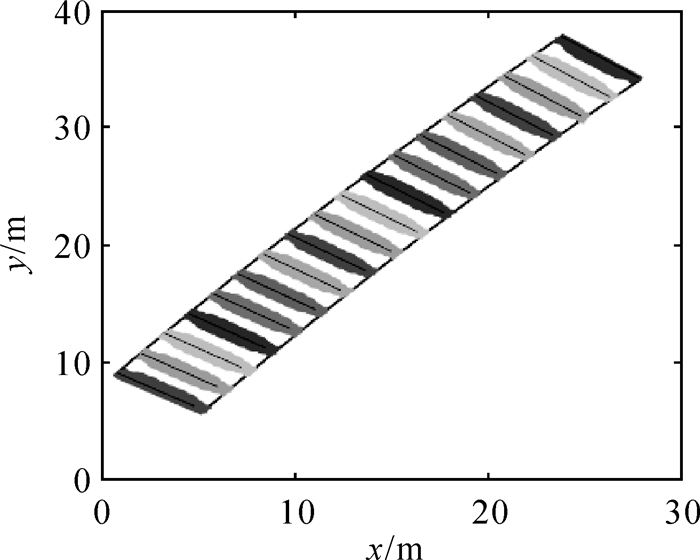
(7) 在此基础上,进行隧道断面点集的自动获取。在中轴线上设置断面的起始截取点为距离隧道口2 m处,截取间隔为2 m,并设置合适的缓冲区半径,计算可以得到每个断面的缓冲区,如图 6所示。然后对每个缓冲区设置距离阈值δ为2 mm,并将阈值δ之内的断面点投影到断面上,最终得到18个横断面点集,如图 7所示。
|
| 图 6 缓冲区 |

|
| 图 7 横断面点集 |
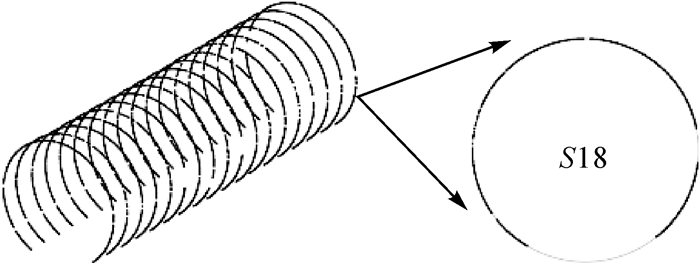
为了更准确地分析隧道的局部和整体的形变情况。按照前文方法进行断面噪声的去除并拟合断面线。图 8所示为去除噪声后的断面点集及断面线拟合的结果(S18表示第18个断面)。
|
| 图 8 去噪及断面线的拟合 |
本次试验区的隧道所采用的拼装管片的内径为5.5 m,且管片拼装的对位限差极其微小,否则相邻管片的连接螺栓不能拧入螺栓套,由此可将隧道内壁的理论半径作为基准值来分析隧道的形变。故对拟合的18个椭圆断面线的长半轴和短半轴进行统计,并分别减去隧道管片的理论半径(2.75 m),得到各断面的横向和纵向最大形变量分布曲线,如图 9所示。从图中可以看出断面的横向最大形变量分布在0~12 mm之间,说明各断面的长半轴均大于管片的理论半径,其中第10个断面位置处具有横向最大拉伸量;纵向最大形变量分布在-22~0 mm之间,说明各断面的短半轴均小于管片的理论半径,其中第6个断面处具有纵向最大收缩量。总体来说,竖直方向的收缩量明显大于水平方向的拉伸量。
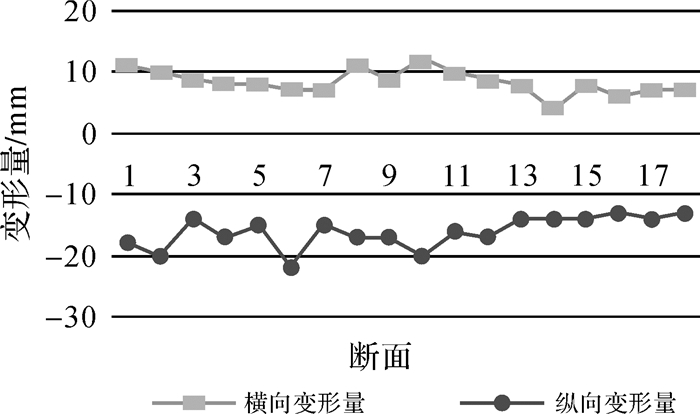
|
| 图 9 断面线横纵向变化量 |
由于各断面线是采用椭圆模型进行拟合的结果,而椭圆度表示断面线接近椭圆的程度,椭圆度越大表示隧道的整体形变越大,根据式(8)即可计算各断面的椭圆度。计算结果见表 1,最大椭圆度为0.011 6%,位于第10个断面处,其中第1、2、6、8个断面位置处,椭圆度均为超过了0.01%,说明这些位置处的断面整体变形较大。
 (8)
(8) | (%) | |||||
| 断面位置 | 椭圆度 | 断面位置 | 椭圆度 | 断面位置 | 椭圆度 |
| 1 | 0.010 5 | 7 | 0.008 0 | 13 | 0.008 0 |
| 2 | 0.010 9 | 8 | 0.010 2 | 14 | 0.006 5 |
| 3 | 0.008 4 | 9 | 0.009 5 | 15 | 0.008 0 |
| 4 | 0.009 1 | 10 | 0.011 6 | 16 | 0.006 9 |
| 5 | 0.008 4 | 11 | 0.009 5 | 17 | 0.007 6 |
| 6 | 0.010 5 | 12 | 0.009 5 | 18 | 0.007 3 |
为了更加精细地分析断面局部的形变情况,计算椭圆度超过0.01%的断面在各个角度上的形变值。首先,以x轴正向为0°方向,以各断面截取点集所在的截面为基准,在断面点集内的0°~360°方向上按逆时针搜索断面点,如果在某一方向搜索不到断面点,则对与该方向线距离在2 cm(最大点密度)之内的若干个点进行局部曲面拟合并求算曲面与该方向线的交点,进而得到该方向上的断面点,如图 10所示。
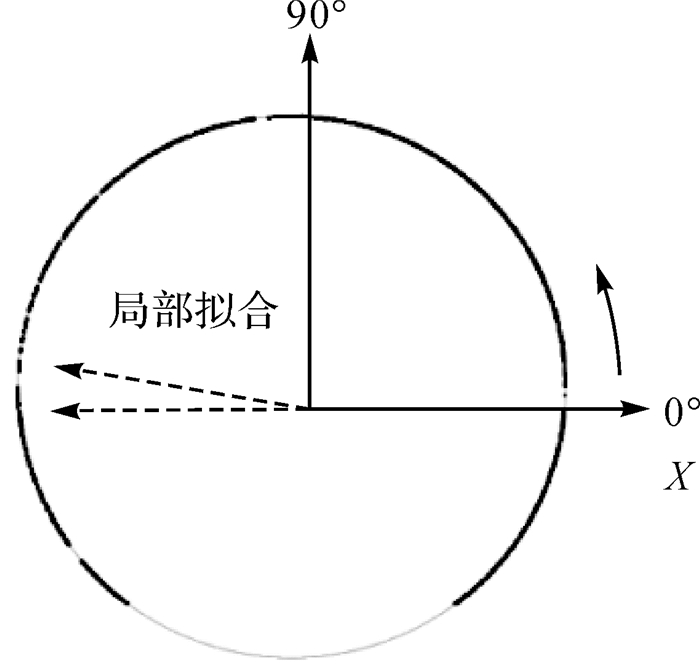
|
| 图 10 各角度断面点的计算 |
计算各方向上的断面点与对应断面中心的距离,并将此距离与管片理论半径进行比较,最终得到断面在任意方向上的形变情况。选择各断面具有代表性的角度上的形变值,以此分析隧道的形变规律。但是受数据采集时附属物对隧道壁遮挡的影响,对附属物进行去噪处理后导致某些方向上2 cm范围内点的缺失,无法生成断面点,用“—”来表示,见表 2。
| mm | |||||||||||
| 位置/m | 方向/(°) | ||||||||||
| 0 | 25 | 50 | 75 | 90 | 115 | 140 | 165 | 180 | 205 | 335 | |
| 1 | 8.7 | 4.4 | -7 | -23.5 | -24.9 | -20.1 | -0.4 | 8.5 | 14.5 | 5.7 | 3.8 |
| 2 | 9.6 | 1.2 | -1.5 | -13.7 | -25.8 | -15.1 | — | 5.4 | 10.4 | 0.5 | 3.4 |
| 6 | — | -1.2 | — | -20.3 | — | -15 | 2.9 | 1.4 | — | -5.1 | 0.5 |
| 8 | 6.6 | 6.1 | -6.5 | -18.9 | -22.5 | -18.4 | -9.2 | -6.2 | 6.3 | 2.1 | 1.9 |
| 10 | — | 5.4 | -15 | -22.4 | -26.5 | -22.9 | -12 | -3.1 | — | 8.5 | 3.7 |
| Mean | 8.3 | 3.18 | -7.5 | -19.76 | -24.93 | -18.3 | -4.68 | 1.2 | 10.4 | 2.34 | 2.66 |
从表 2中可以看出,各断面在90°方向上形变最大;其次为90°方向两侧即75°和115°方向,且形变量均为负值;然后为0°和180°方向,形变量均为正值;而其他方向的变形量相对较小。以上对结果的各项分析表明,隧道在拱顶及其周围所受压力较大使得隧道断面整体变形成为一个扁圆形。
4 结语本文研究了基于移动激光扫描的点云数据的地铁隧道形变分析方法,并将其应用在实际的隧道中,分析了各断面的整体形变情况及椭圆度较大的断面在各方向上的形变情况。在中轴线的提取过程中,基于原始点云数据直接提取隧道的中轴线,避免了以往方法中需要将大量的隧道点云旋转再提取中轴线的过程,减小了计算量;在隧道横断面截取过程中,通过构建每个断面的缓冲区对原始点云进行分块处理,再进行断面点集的加密,在提高断面点集密度的同时也加快了断面的获取速度;此外,提出了一种迭代椭圆拟合的断面噪声去除方法,在拟合出隧道断面曲线的同时去除了非隧道壁上的噪声,效果较好。通过采用全站仪测量里程K27+300处的横断面与本文的方法提取的断面的对比分析表明,两种方法获取的断面横向和纵向最大变形差均小于4.8 mm,验证了该方法的可行性。该方法既可以用于换站拼接后的点云数据,也可以直接用于移动激光扫描技术获取的隧道点云数据,效果较好。但方法中仍然存在着很多不足,首先,原始的隧道点云数据中存在很多非隧道壁上的点,因此在隧道中轴线的提取过程中,虽然采用了抗噪效果较好的随机抽样一致性算法进行曲线拟合,但拟合结果中必然存在着误差,对断面的提取精度有一定的影响;其次,后期的断面去噪方法虽然有效去除了非隧道壁上的噪声,但设置单一的阈值在去除噪点的同时也可能删除了某些细微的形变点。这些问题在后期的研究中都有待进一步解决。
| [1] | 边大勇, 卢小平, 李永强, 等. 地铁盾构区间施工测量技术研究[J]. 测绘通报, 2011(4): 51–55. |
| [2] | 史玉峰, 张俊, 张迎亚. 基于地面三维激光扫描技术的隧道安全监测[J]. 东南大学学报(自然科学版), 2013, 43(S2): 246–249. |
| [3] | CHENG Y, QIU W, LEI J. Automatic Extraction of Tunnel Lining Cross-sections from Terrestrial Laser Scanning Point Clouds[J]. Sensors, 2016, 16(10): 1648–1663. DOI:10.3390/s16101648 |
| [4] | HAN S, CHO H, KIM S, et al. Automated and Efficient Method for Extraction of Tunnel Cross Sections Using Terrestrial Laser Scanned Data[J]. Journal of Computing in Civil Engineering, 2013, 27(3): 274–281. DOI:10.1061/(ASCE)CP.1943-5487.0000211 |
| [5] | 王令文, 程效军, 万程辉. 基于三维激光扫描技术的隧道检测技术研究[J]. 工程勘察, 2013, 41(7): 53–57. |
| [6] | 李珵, 卢小平, 朱宁宁, 等. 基于激光点云的隧道断面连续提取与形变分析方法[J]. 测绘学报, 2015, 44(9): 1056–1062. DOI:10.11947/j.AGCS.2015.20140632 |
| [7] | 吕冰, 钟若飞, 王嘉楠. 车载移动激光扫描测量产品综述[J]. 测绘与空间地理信息, 2012, 35(6): 184–187. |
| [8] | FISCHLER M A, BOLLES R C. Random Sample Consensus:A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography[J]. ACM, 1981, 24(6): 726–740. |
| [9] | 吴丽娟, 郑冕, 张彩明. 海量空间数据点K近邻的快速搜索算法[J]. 小型微型计算机系统, 2007, 28(1): 70–74. |
| [10] | 刘燕萍, 程效军, 贾东峰. 基于三维激光扫描的隧道收敛分析[J]. 工程勘察, 2013, 41(3): 74–77. |
| [11] | WALTON G, DELALOYE D, DIEDERICHS M S. Development of an Elliptical Fitting Algorithm to Improve Change Detection Capabilities with Applications for Deformation Monitoring in Circular Tunnels and Shafts[J]. Tunnelling & Underground Space Technology, 2014, 43(7): 336–349. |
| [12] | 程效军, 贾东峰, 刘燕萍, 等. 基于中轴线的隧道点云去噪算法[J]. 同济大学学报(自然科学版), 2015, 43(8): 1239–1245. DOI:10.11908/j.issn.0253-374x.2015.08.018 |
| [13] | 曾鼎华, 张永兴, 阴可, 等. 三角形量测法在隧道变形监测中的应用研究[J]. 水文地质工程地质, 2005, 32(5): 113–115. |
| [14] | 唐琨, 戴鑫, 黄祖登. 基于三维激光扫描的隧道变形监测方法研究[J]. 地理空间信息, 2016, 14(4): 97–98. |
| [15] | 简骁, 童鹏. 基于地面激光雷达技术的隧道变形监测方法研究[J]. 铁道勘察, 2011, 37(6): 19–22. |
| [16] | HAN J. Monitoring Tunnel Profile by Means of Multi-epoch Dispersed 3D LiDAR Point Clouds[J]. Tunnelling & Underground Space Technology, 2013, 33(1): 186–192. |
| [17] | HAN J, GUO J, JIANG Y. Monitoring Tunnel Deformations by Means of Multi-epoch Dispersed 3D LiDAR Point Clouds:An Improved Approach[J]. Tunnelling & Underground Space Technology, 2013, 38(9): 385–389. |
| [18] | 托雷, 康志忠, 谢远成, 等. 利用三维点云数据的地铁隧道断面连续截取方法研究[J]. 武汉大学学报(信息科学版), 2013, 38(2): 171–175. |
| [19] | KANG Z, ZHANG L, LEI T, et al. Continuous Extraction of Subway Tunnel Cross Sections Based on Terrestrial Point Clouds[J]. Remote Sensing, 2014, 6(1): 857–879. DOI:10.3390/rs6010857 |
| [20] | GOSLIGA R, LINDENBERGH R, PFEIFER N. Deformation Analysis of a Bored Tunnel by Means of Terrestrial Laser Scanning[J]. IAPRS, 2006(XXXVI): 167–172. |
| [21] | 张迪, 钟若飞, 李广伟, 等. 车载激光扫描系统的三维数据获取及应用[J]. 地理空间信息, 2012, 10(1): 20–21. |
| [22] | EDELSBRUNNER H, KIRKPTRICK D, SEIDEL R. On the Shape of a Set of Points in the Plane[J]. IEEE Transactions on Information Theory, 1983, 29(4): 551–559. DOI:10.1109/TIT.1983.1056714 |
| [23] | DOFOUR A, TANKYEVYCH O, NAEGEL B, et al. Filtering and Segmentation of 3D Angiographic Data:Advances Based on Mathematical Morphology[J]. Medical Image Analysis, 2013, 17(2): 147–164. DOI:10.1016/j.media.2012.08.004 |
| [24] | POCK T, BEICHEL R, BISCHOF H. A Novel Robust Tube Detection Filter for 3D Centerline Extraction[C]//Scandinavian Conference on Image Analysis. [S. l. ]: Springer-Verlag, 2005: 481-490. |
| [25] | 琚俏俏, 程效军, 徐工. 基于椭圆拟合的隧道点云去噪方法[J]. 工程勘察, 2014, 42(9): 69–72. |
| [26] | 卢小平, 朱宁宁, 禄丰年. 基于椭圆柱面模型的隧道点云滤波方法[J]. 武汉大学学报(信息科学版), 2016, 41(11): 1476–1482. |



