Download PDF  
文章快速检索  
  高级检索
引用本文
于烨，张慧君，李孝辉。顾及钟差随机项的GPS卫星钟差预报[J]. 测绘通报，2018(6)：1-6. DOI: 10.13474/j.cnki.11-2246.2018.0166.
YU Ye, ZHANG Huijun, LI Xiaohui. GPS Satellite Clock Bias Prediction Method Considering Random Items of Clocks Bias[J]. Bulletin of Surveying and Mapping, 2018(6): 1-6. DOI: 10.13474/j.cnki.11-2246.2018.0166.
顾及钟差随机项的GPS卫星钟差预报
于烨1,2,3, 张慧君1,2,4, 李孝辉1,2,4     
1. 中国科学院国家授时中心, 陕西 西安 710600;
2. 中国科学院精密导航定位与定时技术重点实验室, 陕西 西安 710600;
3. 中国科学院大学, 北京 100049;
4. 中国科学院大学天文与空间科学学院, 北京 100049
收稿日期：2017-12-25; 修回日期：2018-01-22
基金项目：国家自然科学基金（11503030）；国防创新基金面上项目（CXJJ-16M205）；中国科学院"西部之光"人才培养计划支持项目（Y507YR0501）
作者简介：于烨(1989-), 男, 硕士生, 主要研究方向为钟差预报和精密导航定位技术。E-mail:yuye115@mails.ucas.edu.cn
摘要：针对卫星钟差呈趋势项和随机项变化的特点，提出了基于GM（1，1）与自回归求和移动平均的组合预报模型。该模型首先采用GM（1，1）模型预报钟差的趋势项部分，然后利用ARIMA模型对GM（1，1）的模型残差序列进行建模和预报，最后将GM（1，1）和ARIMA模型的预报结果对应相加即得到钟差的最终预报值。此外，采用IGS公布的精密卫星钟差进行预报试验，通过与卫星钟差预报中常用的二次多项式模型和修正指数曲线法模型预报结果的对比分析，结果表明：该方法可以对GPS卫星钟差进行高精度的中短期预报。用12 h钟差建模时，预报未来6、12、24和48 h的平均预报精度分别为0.71、1.17、1.93和4.38 ns，相比于二次多项式模型的平均预报精度分别提高了29.70%、43.75%、67.62%和76.21%；相比于修正指数曲线法模型的平均预报精度分别提高了18.39%、33.90%、61.40%和70.49%。
关键词：卫星钟差     预报     灰色模型     自回归求和移动平均     组合模型    
GPS Satellite Clock Bias Prediction Method Considering Random Items of Clocks Bias
YU Ye1,2,3, ZHANG Huijun1,2,4, LI Xiaohui1,2,4     
1. National Time Service Center, Chinese Academy of Science, Xi'an 710600, China;
2. Key Laboratory of Precision Navigation and Timing Technology, National Time Service Center, Chinese Academy of Science, Xi'an 710600, China;
3. University of the Chinese Academy of Science, Beijing 100049, China;
4. School of Astronomy and Space Science, University of the Chinese Academy of Science, Beijing 100049, China
Abstract: Based on the characteristics of the trend and random items of the satellite clock bias(SCB), a combination prediction model based on grey model(GM(1, 1)) and Autoregressive Integrated Moving Average(ARIMA) is proposed.First, the model uses GM (1, 1) to predict the trend of SCB.Then, the residual sequence of GM(1, 1) model is modeled and predicted by using the ARIMA.Finally, the prediction results of GM (1, 1) and ARIMA are added to obtain the final prediction value of clock bias.In addition, the predictive tests are carried out by using the precision SCB published by IGS(International GNSS Service), and the results are compared with those of the quadratic polynomial model(QPM)commonly used in SCB forecast and using the modified exponential curve method (MECM).The results show that this method can make high-precision short-term and mid-term forecast of GPS SCB.When modeling with 12 h clock bias data to predict the next 6, 12, 18 and 24 h, the average prediction accuracy of the model we proposed is 0.71, 1.17, 1.93 and 4.38 ns, respectively.Compared with the mean prediction accuracy of QPM, the accuracy of the prediction was increased by 29.70%, 43.75%, 67.62% and 76.21%, respectively.Compared with the mean prediction accuracy of MECM, the accuracy of the prediction was increased by 18.39%, 33.90%, 61.40% and 70.49%, respectively.
Key words: satellite clock bias     prediction     GM(1, 1)     ARIMA     combination model    

在全球卫星导航系统中，星载原子钟的钟差预报在优化导航电文中的钟差参数、满足实时动态精密单点定位的需求和提供卫星自主导航所需的先验信息方面具有重要作用[1-4]。但是，由于星载原子钟非常敏感，极易受到外界和自身因素变化的影响而很难掌握其复杂细致的变化规律。因此，建立精确的原子钟运行模型变得非常困难，相应的准确预报卫星钟差也非常困难[5-7]。

目前，国内外许多学者在钟差预报方面开展了广泛深入的研究，取得了一系列成果。其中，应用较多的卫星钟差预报模型主要有：二次多项式模型(quadratic polynomial model，QPM)、灰色预报模型(gray model，GM(1, 1))、最小二乘支持向量机模型、人工神经网络模型、卡尔曼滤波模型等[8-13]。这些预报方法分别适用于不同条件下导航卫星原子钟钟差的短期、中长期和长期的预报，但也均有各自的适用范围和局限性。

本文考虑卫星钟差的随机项呈现非平稳变化趋势，提出了GM(1, 1)与ARIMA的组合预报模型。该组合模型首先采用GM(1, 1)模型预报钟差的趋势项，然后利用ARIMA模型对GM(1, 1)模型残差序列进行建模和预报，最后将GM(1, 1)和ARIMA模型的预报结果对应相加即得到钟差的最终预报值。此外，采用IGS公布的事后精密钟差产品进行预报试验，通过与卫星钟差预报中常用的二次多项式模型和修正指数曲线法模型(modified exponential curve method，MECM)预报结果的对比分析，结果表明：该方法可以对GPS卫星钟差进行高精度的中短期预报，验证了该方法的优越性和有效性。

1 GM(1, 1)预报模型

在灰色系统理论中，GM(1, 1)预报模型是最常用的一种灰色系统模型，它是由一个仅包含单变量的一阶微分方程所构成的预报模型，适合对自身数据的预报[14]。

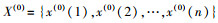
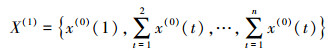设序列为，通过一次累加生成新的序列为

(1)

对累加序列X(1)建立一阶微分方程

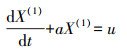(2)

式中，参数a为发展系数；参数u为灰作用量。对式(2)离散化，可得矩阵方程

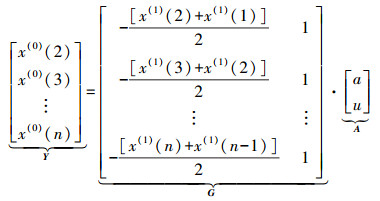(3)

根据最小二乘法可得式(3)的最小二乘解为

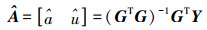(4)

将式(4)代入式(2)即可得预报模型为

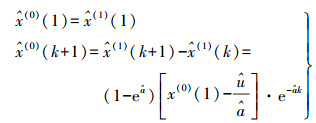(5)

式中，k为参与预报序列的个数。由以上模型即可求得未来任意时刻序列的预报值。

2 ARIMA预报模型

ARIMA(p, d, q)模型常用来做时间序列的预报，适用于平稳时间序列。对于非平稳时间序列需要进行d次差分将非平稳时间序列转化为平稳时间序列，然后对平稳时间序列进行模型定阶和模型参数的估计，最后选择合适的模型阶数建立ARIMA模型进行预报。ARIMA(p, d, q)模型的实质是差分运算与ARMA(p, q)模型的组合[15]。

设有一非平稳时间序列zt，经过d次差分运算已转化为平稳时间序列xt，然后对序列xt建立ARMA(p, q)模型，其定义为

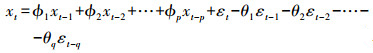(6)

式中，xt为样本；φi(i=1, 2, …, p)为自回归系数；θi(i=1, 2, …, q)为移动平均系数；εt为零均值，方差为σpq2的平稳白噪声序列；p为自回归阶数；q为移动平均阶数。当p=0时，式(6)为MA(q)模型；当q=0时，式(6)为AR(p)模型。

ARIMA模型建立与预报的步骤可归结为如下过程：

(1) 根据时间序列散点图、自相关函数、偏相关函数和ADF单位根检验其方差、趋势变化规律，从而对序列的平稳性进行识别。

(2) 若是非平稳时间序列，需对时间序列进行d次差分处理转化为平稳序列。

(3) 利用平稳时间序列的自相关函数和偏相关函数图确定模型阶数。

(4) 进行模型参数的估计和假设检验。

(5) 选择合适的参数建立ARIMA模型并进行外推预报。

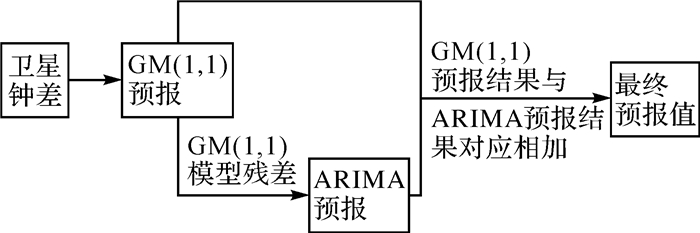
3 组合预报过程

卫星钟差数据序列可以认为是由趋势项和随机项两部分叠加而成，针对它的这一特点，提出了一种基于GM(1, 1)与ARIMA的组合预报模型。运用此组合模型去预报卫星钟差的预报流程如图 1所示，具体步骤如下所述：

图 1 基于GM(1, 1)和ARIMA组合模型的卫星钟差预报流程
图选项

(1) 卫星钟差观测数据预处理。首先剔除卫星钟差观测序列中的异常钟差数据，然后采用拉格朗日插值法将缺失的钟差数据补齐。

(2) 利用GM(1, 1)预报模型提取卫星钟差序列的趋势项，并且对其进行外推预报。

(3) 利用ARIMA预报模型对GM(1, 1)模型的模型残差建模，即对卫星钟差的随机项部分进行建模并外推预报。

(4) 将利用GM(1, 1)模型预报的趋势项序列和利用ARIMA模型预报的随机项序列对应相加，即得到卫星钟差序列最终的预报值。

4 算例与分析 4.1 数据来源

为了验证该组合模型的有效性，从IGS服务器(ftp://cddis.gsfc.nasa.gov/)上下载了2017年3月5日至7日共3天的IGS事后精密钟差产品，其采样间隔为15 min。考虑目前在轨的GPS卫星有30多颗且我国北斗二代系统均搭载的是铷原子钟，因此随机选3颗装载铷原子钟的卫星进行预报试验，它们分别为PRN17(Block ⅡF-M-Rb)、PRN03(Block ⅡF-Rb)和PRN16(Block ⅡR-Rb)号卫星。

4.2 建模方案与结果分析

算例中采用12 h钟差数据(2017年3月5日00:00至12:00)共49个历元，分别建立二次多项式模型(QPM)、修正指数曲线法(MECM)预报模型、GM(1, 1)与ARIMA的组合模型(GM(1, 1)+ARIMA)，对未来6、12、24和48 h的卫星钟差进行中短期预报。

由于本试验使用的是IGS服务器上公布的事后精密钟差产品，其自身的误差小于0.1 ns，故可以作为“真值”，使用均方根误差(RMS)作为统计量，用于检验二次多项式模型、修正指数曲线法预报模型、GM(1, 1)与ARIMA的组合模型所预报结果的准确程度。

将接下来6、12、24和48 h的实际观测钟差数据与各模型预报的钟差数据对应相减即得到预报误差，取各模型预报误差序列的均方根误差(RMS)为衡量预报精度的标准，结果如图 2—图 5和表 1—表 4所示。其中图 2、图 3和图 4分别为用12 h钟差数据建立二次多项式模型、修正指数曲线法预报模型、GM(1, 1)与ARIMA的组合模型预报未来6、12、24和48 h钟差数据的预报误差变化图，图 5为各模型预报钟差的平均预报精度对比图。表 1、表 2和表 3分别为用12 h钟差数据建立二次多项式模型、修正指数曲线法预报模型、GM(1, 1)与ARIMA的组合模型预报未来6、12、24和48 h钟差数据预报误差的最大值(Max)、平均值(Mean)和均方根误差(RMS)统计表。

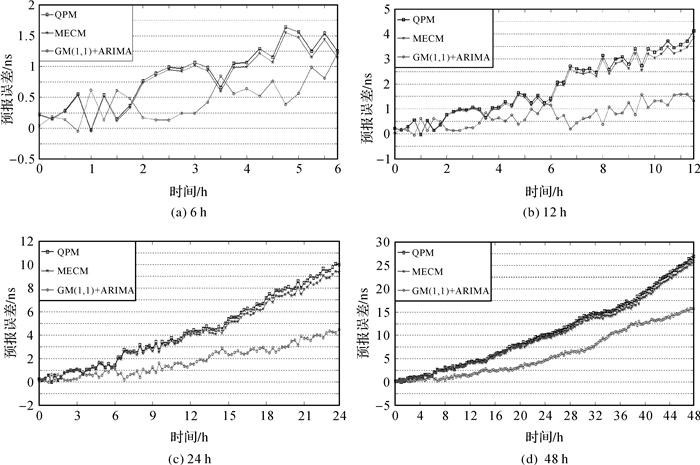
图 2 PRN17用12 h数据建模预报
图选项
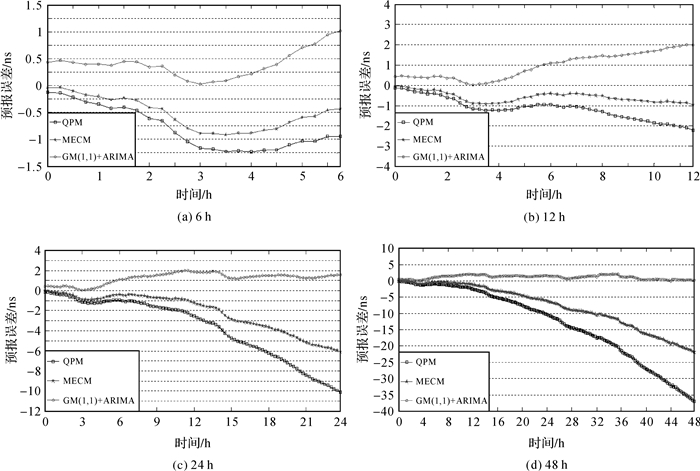
图 3 PRN03用12 h数据建模预报
图选项
图 4 PRN16用12 h数据建模预报
图选项
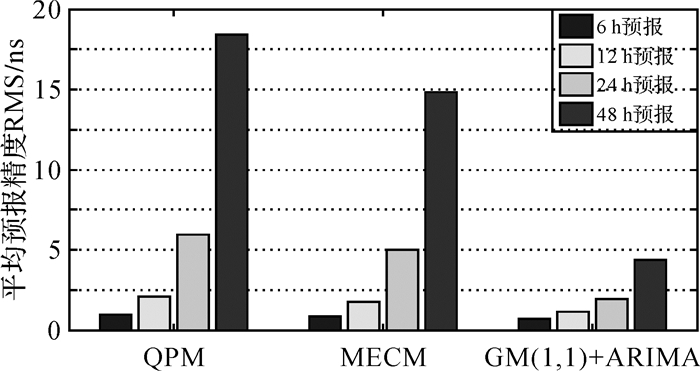
图 5 各模型预报钟差的平均预报精度比较
图选项
表 1 PRN17号卫星各模型预报误差统计结果
预报步长/h 模型 Max
/ns		 Mean
/ns		 RMS
/ns
6 QPM 1.63 0.85 0.97
MECM 1.55 0.79 0.91
GM(1, 1)+ARIMA 1.21 0.45 0.55
12 QPM 4.13 1.88 2.22
MECM 3.87 1.76 2.09
GM(1, 1)+ARIMA 1.59 0.72 0.85
24 QPM 10.06 4.42 5.31
MECM 9.42 4.13 4.97
GM(1, 1)+ARIMA 4.49 1.83 2.22
48 QPM 26.97 10.81 13.18
MECM 25.92 10.20 12.47
GM(1, 1)+ARIMA 15.79 6.10 7.88
表选项
表 2 PRN03号卫星各模型预报误差统计结果
预报步长/h 模型 Max/ns Mean/ns RMS/ns
6 QPM -0.13 -0.80 0.89
MECM -0.04 -0.52 0.60
GM(1, 1)+ARIMA 1.02 0.40 0.48
12 QPM -0.13 -1.15 1.27
MECM -0.04 -0.58 0.64
GM(1, 1)+ARIMA 2.00 0.96 1.14
24 QPM -0.13 -3.73 4.81
MECM -0.04 -2.15 2.86
GM(1, 1)+ARIMA 2.00 1.23 1.34
48 QPM -0.13 -13.08 17.13
MECM -0.04 -7.79 10.23
GM(1, 1)+ARIMA 2.03 1.08 1.23
表选项
表 3 PRN16号卫星各模型预报误差统计结果
预报步长/h 模型 Max/ns Mean/ns RMS/ns
6 QPM 0.42 -0.73 1.18
MECM 0.51 -0.63 1.10
GM(1, 1)+ARIMA 1.67 0.97 1.09
12 QPM 0.42 -2.14 2.76
MECM 0.51 -1.97 2.58
GM(1, 1)+ARIMA 2.34 1.51 1.53
24 QPM 0.42 -6.14 7.75
MECM 0.51 -5.68 7.17
GM(1, 1)+ARIMA 3.56 2.12 2.23
48 QPM 0.42 -19.38 24.91
MECM 0.51 -17.16 21.82
GM(1, 1)+ARIMA 7.21 3.63 4.03
表选项
表 4 精密卫星钟差预报结果的平均RMS
ns
模型 预报长度
6 h 12 h 24 h 48 h
QPM 1.01 2.08 5.96 18.41
MECM 0.87 1.77 5.00 14.84
GM(1, 1)+MECM 0.71 1.17 1.93 4.38
表选项

结合图 2—图 5和分析表 1—表 4的统计量可以看出：在所选择的预报时间长度内，GM(1, 1)与ARIMA组合模型对于PRN03卫星钟差预报的精度最高，其次是PRN17卫星，再次是PRN16卫星，且该组合模型预报的均方根误差均小于二次多项式模型和修正指数曲线法模型预报对应的均方根误差。这说明对于卫星钟差预报，该组合模型较常用的二次多项式模型和修正指数曲线法模型有更高的预报精度和稳定性。在短期预报中，6 h预报的平均预报精度控制在1 ns以内，相比于常用的二次多项式模型，平均预报精度提高了29.70%，相比于修正指数曲线法，平均预报精度提高了18.39%；12 h预报的平均预报精度控制在2 ns以内，相比于常用的二次多项式模型，平均预报精度提高了43.75%，相比于修正指数曲线法，平均预报精度提高了33.90%；24 h预报的平均预报精度控制在2 ns以内，相比于常用的二次多项式模型，平均预报精度提高了67.62%，相比于修正指数曲线法，平均预报精度提高了61.40%。在中长期预报中，48 h预报的平均预报精度控制在5 ns以内，相比于常用的二次多项式模型，平均预报精度提高了76.21%，相比于修正指数曲线法，平均预报精度提高了70.49%。

5 结语

针对卫星钟差呈趋势项和随机项变化的特点，本文将GM(1, 1)模型与ARIMA模型有机地结合起来，建立了一种基于GM(1, 1)与ARIMA的组合模型，并将其应用于卫星钟差的中短期预报。该组合预报模型首先采用GM(1, 1)模型预报卫星钟差序列中的趋势项成分，然后提取出卫星钟差序列中的随机项成分并建立ARIMA模型，最后将两部分预报的结果对应相加即得到卫星钟差的最终预报值。该方法不仅顾及了卫星钟差序列变化的特点，而且充分发挥了GM(1, 1)模型和ARIMA模型各自的优势，具有所需建模数据少、易于实现和计算速度快等优点。从上述预报试验的结果可以看出，该组合模型只需要使用较少的钟差数据建模即可实现高精度的预报，尤其是在中长期的预报中。该方法相比于各单一预报方法，突出了其预报的有效性和优越性，从而验证了该组合方法的有效性和可行性。

参考文献
[1] 王宇谱, 吕志平, 王宁. BDS星载原子钟长期性能分析[J]. 测绘学报, 2009, 46(2): 157–169.
[2] 于烨, 张慧君, 李孝辉. 组合模型在卫星钟差中长期预报中的应用和比较[J]. 电子测量技术, 2017, 40(11): 7–11.
[3] 黄孝增. 基于ARMA模型的GPS钟差预报改进研究[J]. 测绘通报, 2015(S1): 103–105.
[4] 路晓峰. 导航卫星钟差评估与预报研究[D]. 西安: 长安大学, 2007.
[5] 陈正生, 吕志平, 张洁华, 等. 基于时间序列分解的GPS卫星钟差预报[J]. 测绘科学, 2011, 36(3): 116–118.
[6] 郑作亚, 党亚民, 卢秀山, 等. 附有周期项的预报模型及其在GPS卫星钟差预报中的应用研究[J]. 天文学报, 2010, 51(1): 95–102.
[7] 帅平, 曲广吉. 导航星座自主导航的时间同步技术[J]. 宇航学报, 2005, 26(6): 15–28.
[8] 王继刚, 胡永辉, 何在民, 等. 组合模型预报导航卫星钟差[J]. 大地测量与地球动力学, 2012, 32(1): 84–88.
[9] 朱祥维, 肖华, 雍少为, 等. 卫星钟差预报的Kalman算法及其性能分析[J]. 宇航学报, 2008, 29(3): 996–970.
[10] 郭承军, 腾云龙. 基于小波分析和神经网络的卫星钟差预报性能分析[J]. 天文学报, 2010, 51(4): 396–403.
[11] 黄观文, 张勤, 王继刚. GPS卫星钟差的估计与预报研究[J]. 大地测量与地球动力学, 2009, 18(6): 108–122.
[12] 张清华, 隋立芬, 牟忠凯. 基于小波与ARMA模型的卫星钟差预报方法[J]. 大地测量与地球动力学, 2010, 30(6): 100–104.
[13] HAIBO Y, ZHENGMING W, SHAOWU D, et al. Dynamic Grey-autoregressive Model of an Atomic Clock[J]. Metrologia, 2008(6): 1–5.
[14] 崔先强, 焦文海. 灰色系统模型在卫星钟差预报中的应用[J]. 武汉大学学报(信息科学版), 2005, 30(5): 447–450.
[15] 徐君毅, 曾安敏. ARIMA(0, 2, q)模型在卫星钟差预报中的应用[J]. 大地测量与地球动力学, 2009, 29(5): 116–120.
http://dx.doi.org/10.13474/j.cnki.11-2246.2018.0166
国家测绘地理信息局主管、中国地图出版社（测绘出版社）主办。
0

文章信息

于烨，张慧君，李孝辉
YU Ye, ZHANG Huijun, LI Xiaohui
顾及钟差随机项的GPS卫星钟差预报
GPS Satellite Clock Bias Prediction Method Considering Random Items of Clocks Bias
测绘通报，2018(6)：1-6.
Bulletin of Surveying and Mapping, 2018(6): 1-6.
http://dx.doi.org/10.13474/j.cnki.11-2246.2018.0166

文章历史

收稿日期：2017-12-25
修回日期：2018-01-22

相关文章

工作空间