天顶对流层延迟(zenith troposphere delay,ZTD)包括对流层静力延迟(zenith hydrostatic delay,ZHD)和对流层湿延迟(zenith wet delay,ZWD),是GNSS高精度导航定位中的主要误差源[1]。从2005年开始,全球大地测量观测系统(global geodetic observing system,GGOS)Atmosphere分析中心发布天顶对流层格网产品ZWD、ZHD[2-3](纬差2°×经差2.5°)。很多学者利用GGOS对流层格网产品开展了大量研究与应用,包括对流层变化特征[4-5]、全球ZTD模型[6-7]、快速精密定位[8-9]、气象研究[10]等。同时,也有文献研究指出,利用0.5°分辨率的ECMWF气象数据所计算出的ZTD结果更加接近真实情况[11]。由此可知,高空间分辨率的对流层格网产品自然有利于提高后续应用与研究成果精度水平。然而,在实际应用中也会加大数据存储传输难度、降低计算实时性[12]。因此,应综合考虑产品精度、空间特征及数据量要求,定量探讨对流层格网产品的最佳或合理空间分辨率。
综上,为确定ZTD格网产品发布的空间分辨率,本文对GGOS天顶对流层和ECMWF气象格网产品进行研究。首先,顾及非负矩阵分解算法(non-negative matrix factorization, NMF)在数据压缩[13]、特征提取[14-15]等方面的成功应用,引入NMF算法提取对流层格网产品特征维数并针对该算法迭代效率低[16]等不足,提出一种基于随机学习速率矩阵的NMF算法。其次,结合欧洲中尺度天气预报中心(European Center for Medium Range Weather Forecasts,ECMWF)再分析资料(0.125°×0.125°)分析大气可降水量数据(precipitable water vapor,PWV)、地表大气压数据(surface pressure,SP)与ZWD、ZHD相关系数,并通过ZTD经纬向梯度值分组概率,初步确定格网产品发布的空间分辨率。再次,利用所提出的改进NMF算法,提取不同空间分辨率PWV和SP产品的特征维数,并最终确定ZTD格网产品空间分辨率。最后,建议对ZTD格网产品进行NMF分解并直接发布分解后的基矩阵W和系数矩阵H,并分析NMF发布方法的ZTD格网产品压缩效果。
1 改进的非负矩阵分解算法非负矩阵分解是在矩阵中所有元素均为非负数约束条件之下的矩阵降维分解算法。基本原理可以描述为[13-17]:对于任意一个非负矩阵A∈R+{m×n},寻找两个矩阵W∈R+{m×r}、H∈R+{r×n},在保证其元素均为非负的前提下尽量满足A≈WH。由该式可知,待分解矩阵A中的列向量是对W中所有列向量的加权和,而权重系数为H中相应列中的元素,故W称为基矩阵,H称为系数矩阵。
假设噪声矩阵为E∈R+{m×n},则NMF算法的数学模型可以表示为
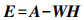 (1)
(1) 由于NMF算法是对待分解矩阵A的优化逼近,故该算法需要在特定目标函数的约束下进行迭代,从而不断逼近待分解矩阵A。目前应用最广泛的目标函数是假设噪声服从正态分布的欧几里得距离[13, 15]
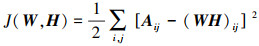 (2)
(2) 式(2)分别对Wik、Hkj两端求导,可得目标函数在Wik、Hkj两方向上的梯度
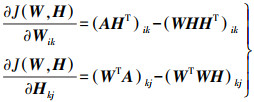 (3)
(3) 根据梯度下降法原理,设学习速率矩阵分别为λW、λH,则基矩阵W和系数矩阵H的迭代式可表示如下
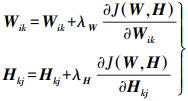 (4)
(4) 在常规学习速率矩阵的基础上,本文提出随机学习速率矩阵
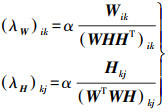 (5)
(5) 式中,α为随机加速因子,α∈0, 1。
将式(5)代入式(4),可得W、H最终迭代估计式为
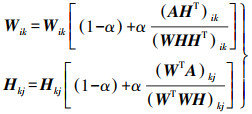 (6)
(6) 本文将式(6)称为基于随机学习速率阵的NMF分解算法。其中,W、H迭代初值一般取0~1均匀分布矩阵,随机加速因子α为[0, 1]均匀分布的随机数,且在每次迭代计算过程中独立生成。显见,当随机加速因子取恒定值α≡1时,式(6)即为标准的NMF分解算法[13, 15]。
2 ZTD格网产品空间分辨率的确定 2.1 ZTD经纬向梯度值概率统计为初步研究天顶对流层数据的空间分布特征,本文对GGOS Atmosphere天顶对流层格网产品(纬差2°×经差2.5°)和ECMWF气象资料(纬差0.125°×经差0.125°)计算等效天顶对流层数据随纬度和经度方向的梯度(纬向和经向差分),从而研究不同空间分辨率ZTD梯度绝对值的概率统计特征,以初步确定ZTD空间分辨率。试验数据选用2015年年积日1、UTC0时的GGOS Atmosphere天顶对流层格网数据和ECMWF提供的气象格网数据PWV、SP,对上述不同分辨率的EZTD和GGOS提供的ZTD格网数据进行梯度计算(方案1:EZTD纬向稀疏后计算梯度,3°×0.125°、2°×0.125°、1°×0.125°、0.5°×0.125°、0.25°×0.125°;方案2:EZTD经向稀疏后计算梯度,0.125°×4°、0.125°×3°、0.125°×2°、0.125°×1°、0.125°×0.5°),并统计梯度绝对值分组概率,所得结果见表 1。从表 1方案1的结果可看出,不同空间分辨率的EZTD格网产品的概率统计特征存在差异,各空间分辨率下小于3 cm的概率统计值分别为81.95%、80.34%、78.85%、78.29%、78.16%,可知纬差1°×经差0.125°是纬向梯度绝对值概率统计特征的空间分辨率拐点。从方案2结果可看出,各空间分辨率下小于3 cm的概率统计值分别为92.20%、91.10%、90.40%、89.67%、89.50%,可得纬差0.125°×经差2°是经向梯度绝对值概率统计特征的空间分辨率拐点。同时,对比方案1和方案2可知,纬向梯度比径向梯度复杂得多,这与文献[7]中的结论一致。因此,初步确定纬差1°×经差2°是保留天顶对流层格网产品特征信息的合理空间分辨率。此外,EZTD与GGOS Atmosphere提供的ZTD格网产品的分组概率统计值及变化趋势比较吻合,进一步验证了结合EZTD数据研究ZTD格网产品空间分辨率的合理性。
| (%) | |||||||||
| 数据源 | 分辨率 | [0, 3) | [3, 6) | [6, 10) | [10, 15) | [15, 20) | [20, 30) | [30, +∞) | |
| 方案1 | GGOS | 2°×2.5° | 76.46 | 12.95 | 5.07 | 2.72 | 1.35 | 1.07 | 0.39 |
| 3°×0.125° | 81.95 | 10.51 | 3.91 | 2.15 | 1.03 | 0.37 | 0.08 | ||
| 2°×0.125° | 80.34 | 11.22 | 4.29 | 2.21 | 1.09 | 0.66 | 0.20 | ||
| EZTD | 1°×0.125° | 78.85 | 11.82 | 4.57 | 2.29 | 1.10 | 1.00 | 0.38 | |
| 0.5°×0.125° | 78.29 | 11.90 | 4.89 | 2.27 | 1.12 | 0.98 | 0.55 | ||
| 0.25°×0.125° | 78.16 | 11.93 | 4.88 | 2.29 | 1.14 | 0.97 | 0.63 | ||
| 方案2 | GGOS | 2°×2.5° | 87.71 | 7.06 | 2.90 | 1.37 | 0.41 | 0.37 | 0.18 |
| 0.125°×4° | 92.20 | 4.98 | 1.88 | 0.60 | 0.14 | 0.20 | 0.00 | ||
| 0.125°×3° | 91.10 | 5.56 | 2.09 | 0.71 | 0.27 | 0.22 | 0.06 | ||
| EZTD | 0.125°×2° | 90.40 | 5.63 | 2.36 | 0.89 | 0.33 | 0.25 | 0.13 | |
| 0.125°×1° | 89.67 | 5.91 | 2.42 | 1.06 | 0.41 | 0.33 | 0.20 | ||
| 0.125°×0.5° | 89.50 | 5.96 | 2.43 | 1.04 | 0.45 | 0.37 | 0.25 | ||
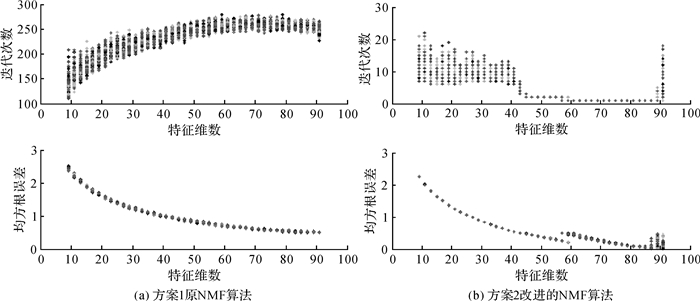
为比较原NMF分解算法和本文所提的基于随机学习速率矩阵的NMF分解算法的优劣,采用2015年年积日1、UTC0时的大气可降水量格网产品PWV(纬差2°×经差2.5°,数据矩阵维数为91×145),进行NMF分解算法改进前后的效果对比分析。其中,特征维数设置为9~91、步长取2,均方根误差和误差下降率阈值分别为0.5 cm、1×10-7。此外,鉴于NMF分解结果的不唯一性,为使对比结果具有统计意义,每个特征维数进行100次重复NMF分解计算。方案1:利用原NMF算法进行迭代分解,统计迭代终止时的迭代次数和均方根误差;方案2:利用改进的NMF算法进行迭代分解,统计迭代终止时的迭代次数和均方根误差。计算结果如图 1所示。
|
| 图 1 两种方法迭代次数和均方根误差 |
从图 1可以看出,改进后NMF算法迭代次数得到了极大减少、迭代终止时的均方根误差也得到了降低,表明基于随机学习速率矩阵的NMF算法优于原NMF算法。其次,原NMF算法在特征维数范围内无法保证迭代收敛,说明该方法不能成功提取PWV的空间特征;而改进的NMF算法在特征维数大于某一值后,能够保证迭代收敛。而特征维数是空间分布特征的直观表达,通过对比不同空间分辨率下的特征维数,能够完整表达PWV空间特征的最佳空间分辨率。因此,下面采用改进的NMF算法进行对流层延迟特征维数的计算分析。
为对比不同分辨率对流层延迟的特征维数,选择2015年4个年积日(冬季DOY1、春季DOY90、夏季DOY182和秋季DOY274)、每日UTC0与UTC12时共8个时刻的可降水量产品PWV、地表大气压产品SP(纬差0.125°×经差0.125°),进而对PWV和SP数据进行稀疏化,得到纬差×经差分别为2.5°×5°、2°×2.5°、2°×2°、1°×2°、1°×1°、0.5°×1°、0.5°×0.5°共7种空间分辨率的全球格网产品,分别对PWV、SP数据进行NMF分解(均方根误差和误差下降率阈值分别为0.5 cm、1×10-7)并研究特征维数与空间分辨率的关系。需说明的是,PWV与SP数据已转换为等效ZWD与等效ZHD(单位:厘米)。表 2为相应的PWV固有特征维数统计结果。表 3为相应的PWV固有特征新维数统计结果。
| UTC | 年积日 | 空间分辨率(纬差×经差) | ||||||
| 2.5°×5° | 2°×2.5° | 2°×2° | 1°×2° | 1°×1° | 0.5°×1° | 0.5°×0.5° | ||
| 0 h | 1 | 30 | 34 | 35 | 36 | 36 | 36 | 36 |
| 90 | 31 | 35 | 35 | 36 | 36 | 36 | 36 | |
| 182 | 35 | 39 | 39 | 42 | 42 | 42 | 42 | |
| 274 | 31 | 37 | 37 | 40 | 40 | 40 | 40 | |
| 12 h | 1 | 32 | 36 | 36 | 38 | 38 | 38 | 38 |
| 90 | 31 | 35 | 35 | 36 | 36 | 36 | 36 | |
| 182 | 35 | 39 | 39 | 42 | 42 | 42 | 42 | |
| 274 | 33 | 39 | 39 | 39 | 40 | 40 | 40 | |
| UTC | 年积日 | 分辨率(纬差×经差) | ||||||
| 2.5°×5° | 2°×2.5° | 2°×2° | 1°×2° | 1°×1° | 0.5°×1° | 0.5°×0.5° | ||
| 0 h | 1 | 43 | 57 | 59 | 70 | 74 | 76 | 77 |
| 90 | 45 | 57 | 59 | 70 | 74 | 77 | 77 | |
| 182 | 43 | 57 | 59 | 70 | 74 | 76 | 77 | |
| 274 | 43 | 57 | 59 | 70 | 74 | 76 | 77 | |
| 12 h | 1 | 43 | 57 | 59 | 70 | 74 | 76 | 77 |
| 90 | 43 | 57 | 59 | 70 | 74 | 77 | 77 | |
| 182 | 45 | 57 | 59 | 70 | 74 | 77 | 77 | |
| 274 | 43 | 57 | 59 | 70 | 74 | 76 | 76 | |
表 2统计了不同时刻、不同分辨率PWV固有特征维数。对比同一年积日不同UTC下的特征维数,可以发现不同UTC的空间特征基本保持不变,表现为全球范围内大气可降水量的短时稳定性。同时,对比同一UTC不同年积日下的空间特征,不同季节的特征维数存在细小差异:夏季的空间特征最为复杂,其固有特征维数为42,春季、冬季的固有特征维数为36,空间特征最简单,说明不同季节大气可降水量的空间分布特征存在差异,从侧面反映了全球范围的季节性差异。
为了分析SP特征维数稳定性与格网间距的关系,表 3统计了不同时刻、不同空间分辨率SP固有特征维数。从该表可以得出,SP特征维数稳定性高于PWV,不同UTC、不同季节的特征维数基本保持不变,而且随着格网间距降至1°以后特征维数基本稳定。此外,同一空间分辨率下、不同时刻之间的特征维数变现出较高的一致性,这也从侧面说明了地表大气压在全球范围内具有较高的稳定性。
综合上述分析,PWV和SP数据的最佳分辨率均为1°×2°,固有特征维数分别为42、70。需指出的是,产品发布若采用原有的发布形式会导致数据量增大(数据矩阵由91×145增大为181×181,后者为前者的2.48倍),而数据量激增不利于存储效率和传输速度。顾及ZWD固有特征维数为42、ZHD有特征维数为70,故经NMF分解后的基矩阵与系数矩阵可获得较好数据压缩效果(详细分析见表 4)。因此,本文建议GGOS Atmosphere对流层格网产品的空间分辨率应采用1°×2°,发布数据内容为格网产品经NMF算法分解后的基矩阵和系数矩阵。
| 指标 | 分辨率 | ||
| 2°×2.5° | 1°×2° | ||
| ZWD | ZHD | ||
| 原数据量 | 13 195 | 32 861 | 32 761 |
| NMF数据量 | — | 14 480 | 25 340 |
| 原压缩比 | — | 2.5 | 2.5 |
| NMF压缩比 | — | 1.1 | 1.9 |
为评价NMF的数据压缩效果,表 4统计了原发布方法和NMF发布新方法的数据量以及数据压缩比。其中,原压缩比为分辨率为1°×2°与2°×2.5°原发布方法数据量的比值,NMF压缩比为1°×2°分辨率NMF发布方法与2°×2.5°分辨率原发布方法数据量的比值。不难看出,对流层格网产品采用1°×2°分辨率会导致数据量变为原来的2.5倍,而采用NMF发布形式的NMF压缩比分别为1.1、1.9,NMF发布方法数据压缩效率达到56%、24%。
3 结论(1) 针对常规非负矩阵分解算法计算效率低、难以提取固有特征维数的问题,基于随机学习速率矩阵,本文提出了一种改进的非负矩阵分解算法。计算结果表明所提出的改进算法迭代效率高、迭代收敛误差小。
(2) 分析了ECMWF PWV、SP与GGOS ZWD、ZHD产品之间的强相关性,结合GGOS ZTD和ECMWF EZTD计算了经向、纬向梯度值分组概率并初步确定了ZTD格网产品的空间分辨率,在此基础上利用NMF算法提取了7种空间分辨率、8个时刻PWV、SP的特征维数,从而确定了ZWD和ZHD格网产品的固有特征维数和最佳空间分辨率。
(3) 建议ZTD格网产品发布的空间分辨率调整为1°×2°,以更好地描述ZTD空间分布特征。同时,针对空间分辨率提高导致的数据量增大问题,推荐对产品进行NMF分解并直接发布分解后的基矩阵W和系数矩阵H,可使ZWD和ZHD压缩效率分别达到56%、24%。
| [1] | LI W, YUAN Y, OU J, et al. New Versions of the BDS/GNSS Zenith Tropospheric Delay Model IGGtrop[J]. Journal of Geodesy, 2015, 89(1): 73–80. DOI:10.1007/s00190-014-0761-5 |
| [2] | 陈俊勇, 党亚民. 完善大地坐标框架和地球重力场时变测量的进展——2005年国际大地测量协会(IAG)科学大会札记[J]. 测绘通报, 2005(12): 1–4. DOI:10.3969/j.issn.0494-0911.2005.12.001 |
| [3] | CHEN Q, SONG S, HEISE S, et al. Assessment of ZTD Derived from ECMWF/NCEP Data with GPS ZTD over China[J]. GPS Solutions, 2011, 15(4): 415–425. DOI:10.1007/s10291-010-0200-x |
| [4] | ZHANG J Y, WANG L, YANG S, et al. Decadal Changes of the Wintertime Tropical Tropospheric Temperature and Their Influences on the Extratropical Climate[J]. Science Bulletin, 2016, 61(9): 737–744. DOI:10.1007/s11434-016-1054-6 |
| [5] | YUCHECHEN A E, LAKKIS S G, LAVORATO M B. On the Stability of the Troposphere/Lower Stratosphere and Its Relationships with Cirrus Clouds and Three Mandatory Levels over Buenos Aires[J]. International Journal of Remote Sensing, 2016, 37(7): 1541–1552. DOI:10.1080/01431161.2016.1154221 |
| [6] | 姚宜斌, 何畅勇, 张豹, 等. 一种新的全球对流层天顶延迟模型GZTD[J]. 地球物理学报, 2013, 56(7): 2218–2227. DOI:10.6038/cjg20130709 |
| [7] | 姚宜斌, 胡羽丰, 张豹. 利用多源数据构建全球天顶对流层延迟模型[J]. 科学通报, 2016, 61(24): 2730–2741. |
| [8] | 高旺, 高成发, 潘树国, 等. 北斗三频宽巷组合网络RTK单历元定位方法[J]. 测绘学报, 2015, 44(6): 641–648. DOI:10.11947/j.AGCS.2015.20140308 |
| [9] | AHMED F, VÁCLAVOVIC P, TEFERLE F N, et al. Comparative Analysis of Real-time Precise Point Positioning Zenith Total Delay Estimates[J]. GPS Solutions, 2016, 20(2): 187–199. DOI:10.1007/s10291-014-0427-z |
| [10] | DOUSA J, VACLAVOVIC P. Real-time Zenith Tropospheric Delays in Support of Numerical Weather Prediction Applications[J]. Advances in Space Research, 2014, 53(53): 1347–1358. |
| [11] | JIN S, LUO O F, GLEASON S. Characterization of Diurnal Cycles in ZTD from a Decade of Global GPS Observations[J]. Journal of Geodesy, 2009, 83(6): 537–545. DOI:10.1007/s00190-008-0264-3 |
| [12] | 陈钦明, 宋淑丽, 朱文耀. 亚洲地区ECMWF/NCEP资料计算ZTD的精度分析[J]. 地球物理学报, 2012, 55(5): 1541–1548. DOI:10.6038/j.issn.0001-5733.2012.05.011 |
| [13] | LEE D D, SEUNG H S. Learning the Parts of Objects by Non-negative Matrix Factorization[J]. Nature, 1999, 401(6755): 788–91. DOI:10.1038/44565 |
| [14] | 杜海顺, 张旭东, 等. 图嵌入正则化投影非负矩阵分解人脸图像特征提取[J]. 中国图象图形学报, 2014, 19(8): 1176–1184. DOI:10.11834/jig.20140809 |
| [15] | 施蓓琦, 刘春, 孙伟伟, 等. 应用稀疏非负矩阵分解聚类实现高光谱影像波段的优化选择[J]. 测绘学报, 2013, 42(3): 351–358. |
| [16] | 李乐, 章毓晋. 非负矩阵分解算法综述[J]. 电子学报, 2008, 36(4): 737–743. |
| [17] | ZHAN C, LI W, OGUNBONA P. Local Representation of Faces through Extended NMF[J]. Electronics Letters, 2012, 48(7): 373–375. DOI:10.1049/el.2012.0015 |
| [18] | YAO Y, XU C, ZHANG B, et al. GTM-Ⅲ:a New Global Empirical Model for Mapping Zenith Wet Delays onto Precipitable Water Vapour[J]. Geophysical Journal International, 2014, 197(1): 202–212. DOI:10.1093/gji/ggu008 |
| [19] | ZHANG D, GUO J, CHEN M, et al. Quantitative Assessment of Meteorological and Tropospheric Zenith Hydrostatic Delay Models[J]. Advances in Space Research, 2016, 58(6): 1033–1043. DOI:10.1016/j.asr.2016.05.055 |
| [20] | 苗启广, 王宝树. 图像融合的非负矩阵分解算法[J]. 计算机辅助设计与图形学学报, 2005, 17(9): 2029–2032. |


