影像匹配实质上是指两幅或多幅影像之间通过相关函数确定同名特征,一般为点匹配、线匹配和面匹配,其中直线匹配是目前摄影测量和计算机视觉领域研究的热点和难点[1-4]。目前,直线匹配研究多侧重于两个方面:一方面是寻找有效的几何约束用于确定匹配候选,常用的约束条件有同名三角网约束[5-8]、同名点约束[9-10]、单应矩阵约束[11-12]、极线约束[13-15]等。这些约束条件将搜索影像上候选直线局限在设定的条件范围内,减少全局范围匹配搜索时间,提高匹配效率。娄安颖等[12]结合单应矩阵约束和邻域窗口灰度相似性确定同名直线;梁艳等[16]结合同名点约束和邻域窗口灰度均值相关确定同名直线。然而上述这些方法更多侧重于几何约束,后续相似性计算大都直接利用直线邻域窗口灰度信息,这种直接利用影像灰度信息的相似性计算方法对于影像视角变化较大或纹理复杂的影像难以获得可靠的匹配结果。另一方面是直线描述子的构建,近几年直线描述子成为匹配的研究热点,类似于SIFT算子[17],利用直线邻域内点的梯度等信息构建线描述子,取得较大的进展。缪君等提出将待匹配直线离散为若干点的集合[18],根据直线方向和长度定义描述子的主方向和长度,统计离散点邻域梯度信息构建128维描述子,得到n×128的描述子矩阵,n为直线上采样点数目。该描述子仅利用直线上的点构建描述子,舍弃直线邻域范围内的点,对于复杂地物影像,可靠性有待提高。在无任何几何约束条件下,王志衡等提出了具有平移、旋转、光照不变性的梯度幅值均值-标准差描述子(magnitude mean-standard deviation descriptor, MMSD),用于直线匹配[19]。与直接基于灰度窗口相关相比,该描述子具有较好可区分性,能取得较好的直线匹配结果。但这种无需任何几何约束,单一利用描述子的直线匹配方法对于拍摄倾角较大的复杂地物纹理影像,不仅耗时而且匹配可靠性有待提高。
因此,本文在已有MMSD描述子基础上,提出一种结合几何约束和梯度描述子的直线段匹配算法。在已有可靠同名点的基础上,利用同名三角网和核线约束确定匹配候选,以目标直线和候选直线对应的重叠段为中心建立直线支撑域,并利用高斯卷积函数对梯度幅值进行加权处理用于候选描述子构建,保证了直线匹配的可靠性。
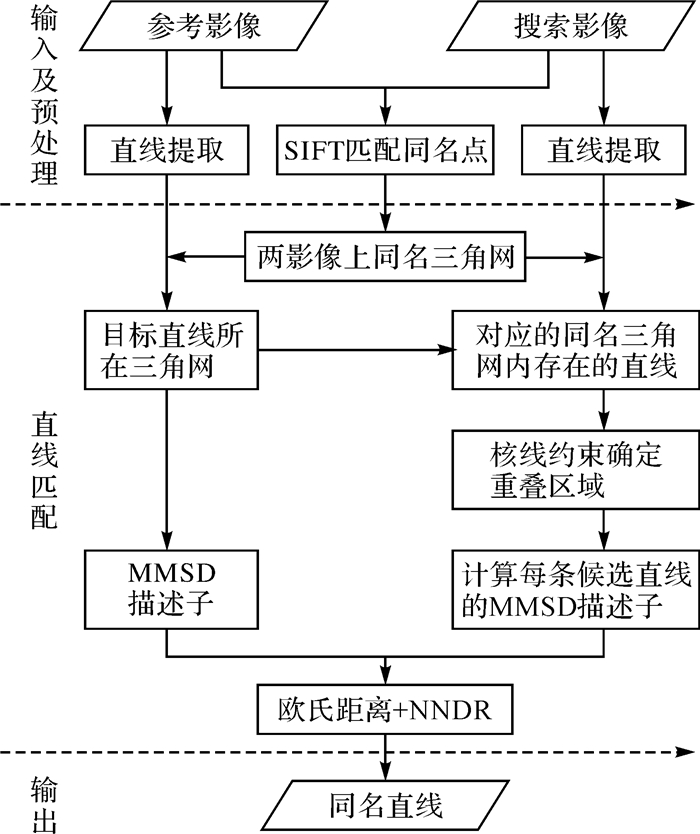
1 技术流程结合几何约束和梯度描述子的直线匹配算法,整理流程如图 1所示。
|
| 图 1 直线匹配流程 |
(1) 首先利用SIFT算子对两张影像进行匹配,并采用RANSAC算法对结果进行误匹配剔除,得到初始可靠同名点,同时对参考影像、搜索影像进行直线提取。
(2) 为了提高直线匹配效率及正确率,取代传统穷举法匹配策略,本文利用同名点构建参考影像、搜索影像上同名三角网,用于约束后续匹配,缩小候选直线搜索范围。
(3) 在此基础上进行核线约束,一方面用于进一步筛选候选直线,另一方面用于确定搜索影像上候选直线与目标直线对应的重叠部分。
(4) 对目标直线和每条候选直线分别建立MMSD描述子。对目标直线直接构建MMSD描述子;对每条候选直线,分别以其对应目标直线的重叠部分为中心构建MMSD描述子。
计算目标直线与候选直线描述子之间的欧氏距离,并结合最小欧氏距离和最近邻距离比率(nearest neighbor distance ratio,NNDR),确定同名直线。
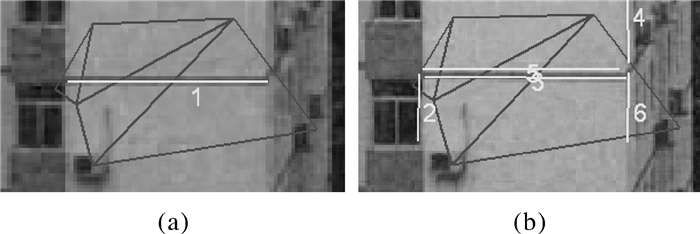
2 约束条件 2.1 同名三角网约束三角网约束指同名直线应位于同名三角网中。利用初始匹配获取同名点构建参考影像、搜索影像上同名三角网。首先确定参考影像上目标直线经过的三角形,对应的将搜索影像上同名三角形中存在的直线作为该目标直线的匹配候选直线。如图 2(a)为参考影像上索引为1的直线段经过的三角形,图 2(b)为搜索影像上对应的同名三角形内经过的直线,索引号分别为2、3、4、5、6。
|
| 图 2 三角网约束 |
为了提高匹配的效率,进一步利用核线约束对上述三角网约束确定的候选直线进行剔除与选择。同时为了提高描述子的可靠性,确保两张影像上对应直线描述子构建的区域一致性,以目标直线为基础,需要利用核线确定候选直线与目标直线对应的重叠直线区域,如图 3所示。
|
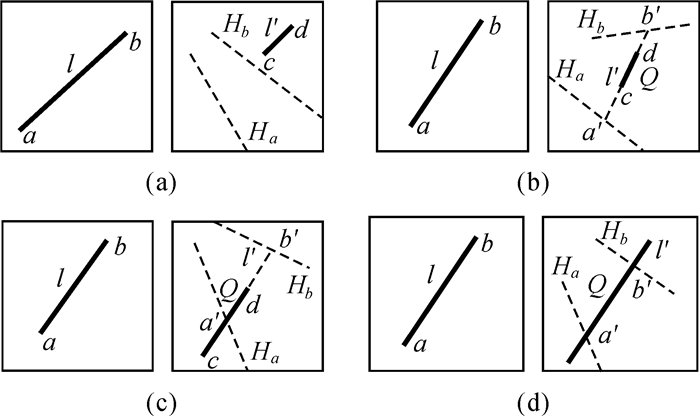
| 图 3 核线约束 |
图 3中,l、l′分别为参考影像上目标直线段和搜索影像上候选直线段,两直线段端点分别为a、b和c、d。计算目标直线段l两端点a、b在搜索影像上的核线Ha、Hb,则搜索影像上候选直线l′与两核线相交的交点为对应的同名端点,两端点连线即为候选直线与目标直线对应的重叠区域。确定候选直线与目标直线对应的重叠区域,一般可分为以下4种情况:
(1) 当候选直线位于核线Ha、Hb范围之外,说明候选直线与目标直线没有重叠部分,将其剔除,如图 3(a)所示。
(2) 当候选直线位于两核线之间,延长其两边端点至核线Ha、Hb上,交点为a′、b′,则延长后的直线段a′b′为对应的重叠区域,如图 3(b)所示。
(3) 当候选直线段与其中一条核线相交,如图 3(c)所示,l′与核线Ha相交,则交点a′为重叠段的一个端点,延长直线另一端与核线Hb相交,交点b′为重叠段的另一个端点,至此,对应的直线重叠区域a′b′已经确定。
(4) 当候选直线段与两条核线均相交,交点a′、b′,则认为直线段a′b′为对应的直线重叠区域,如图 3(d)所示。
3 直线匹配 3.1 梯度幅值描述子构建以目标直线和候选直线对应的重叠区域为基础,对目标直线和候选直线分别构建高斯卷积梯度幅值的均值-标准差描述子。描述子具体构建过程如下:
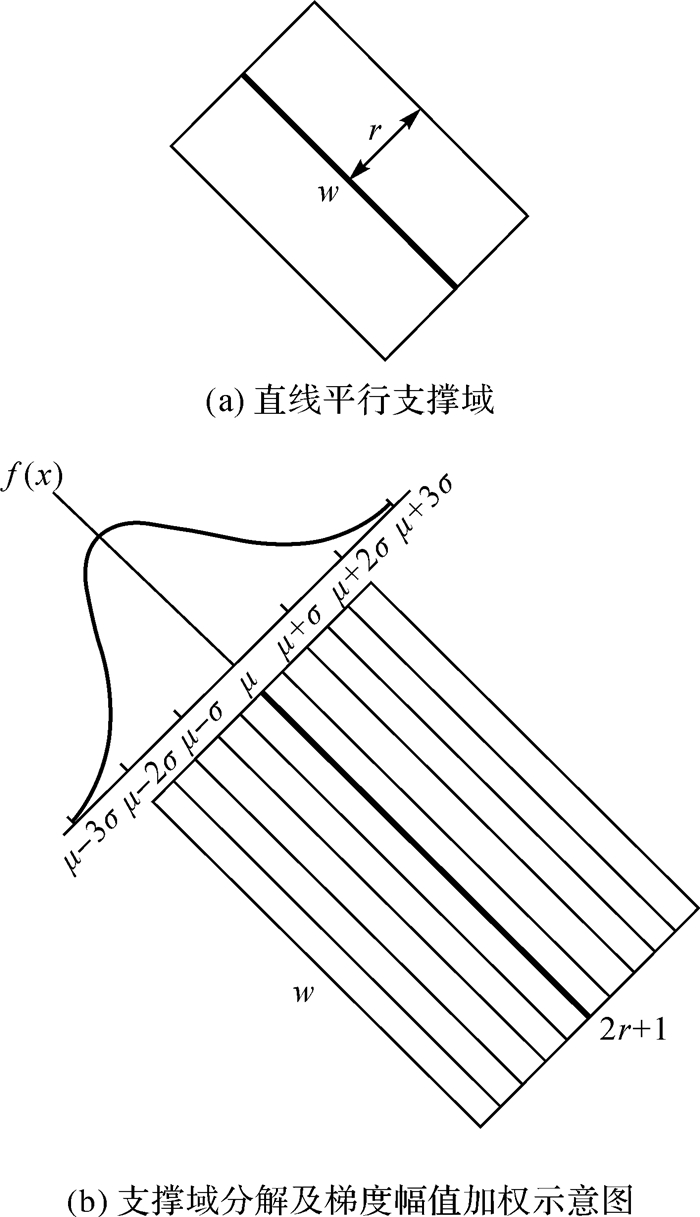
假定任一直线段L,长度为w,以其为中心轴建立如图 4(a)所示的长为w,宽为2r+1的矩形直线支撑域,并将其分解为2r+1条等长的平行直线段,如图 4(b)所示。对于候选直线,需要根据前文中核线确定的同名端点为基础,确保候选直线支撑域方向与目标直线支撑域方向一致。
|
| 图 4 直线平行支撑域及分解 |
根据梯度算子计算矩形直线支撑域内每个像素在水平和垂直方向上的梯度Gx和Gy,并计算每个像素点的梯度幅值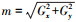
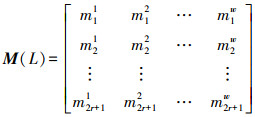 (1)
(1) 式中,mij为第i行第j个点的梯度幅值。为了提高描述子的可靠性,赋予矩阵M(L)中每个像素梯度幅值一个权重,距离直线越近权值越大,对描述子的影响越大,作用越大;反之,距离直线越远权重值越小,对描述子的影响越小,作用越小。权值函数采用高斯函数,公式如下
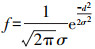 (2)
(2) 式中,d为点到直线距离;σ为支撑域长度的一半。对矩阵M(L)每一列进行高斯加权,则经过加权之后的梯度幅值矩阵为
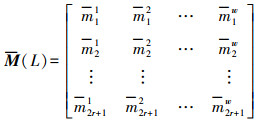 (3)
(3) 为了使描述子的构建与直线长度无关,计算矩阵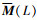
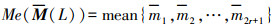 (4)
(4) 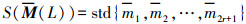 (5)
(5) 为使描述子不受光照影响,分别对上述均值和标准差向量进行归一化处理,得到直线L的梯度幅值描述子
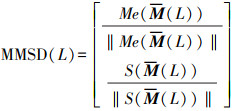 (6)
(6) 因梯度幅值本身具有旋转不变性,因此MMSD描述子具有平移旋转不变性、光照不变性等优点。
3.2 匹配策略本文结合最小欧氏距离和最近邻距离比率NNDR确定同名直线。NNDR是指目标直线与候选直线最近的欧氏距离与次最近欧氏距离的比值,其值小于设定的阈值则认为与目标直线特征欧氏距离最近的候选直线为目标直线的同名直线。
设目标直线梯度描述子为l1, l2, l3, …, lk,候选直线的梯度描述子为r1, r2, r3, …, rk,则二者欧氏距离计算公式如下
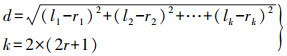 (7)
(7) 计算目标直线与其对应的所有候选直线描述子之间的欧氏距离,设最近距离为d1,次近距离为d2,则确定同名直线的判断条件为
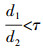 (8)
(8) 即当比值小于τ则判定距离目标直线特征最近的候选直线为最终的同名直线。
4 试验及分析为验证本文梯度幅值描述子具有旋转不变性、光照不变性及其稳健性,本文选取三组近景影像和一组航空影像进行直线匹配试验。如图 5所示,其中图 5(a)、图 5(b)为存在旋转变化的影像对,图 5(c)为光照不同的影像对,图 5(d)为建筑物区域航空影像对。同时为了进行对比分析,本文还实现了另外两种算法的直线匹配试验:①无约束条件下的MMSD描述子直线匹配;②相同约束条件下,基于灰度均值标准差描述子(gray mean-standard deviation descriptor,GMSD)的直线匹配。鉴于文章篇幅,文中仅显示本文算法对上述四组影像进行直线匹配的结果,如图 6所示,其中黑色线为正确匹配直线,粗线为错误匹配直线。直线提取及匹配结果统计见表 1,通过人工目视判读方法判断匹配结果正确与否,表中MN(matching number)表示匹配直线的总数目,EM(error matching)表示错误匹配数目,CR(correct ratio)表示匹配正确率。试验过程中,NNDR阈值τ设定为0.8,直线支撑域建立过程中r=10。

|
| 图 5 试验影像 |
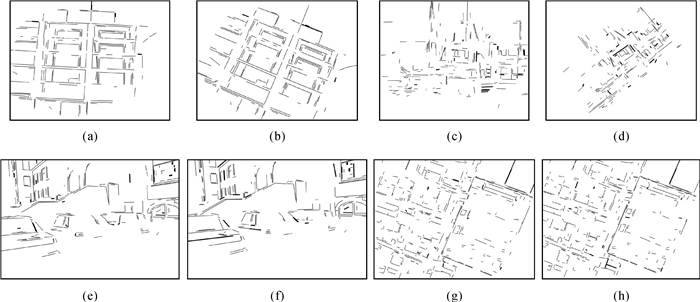
|
| 图 6 本文算法直线匹配结果 |
| 影像 | 提取直线数目 | 描述子 | MN | EM | CR/(%) |
| GMSD | 229 | 12 | 94.7 | ||
| 图 5(a) | 471/477 | 无约束MMSD | 121 | 37 | 69.4 |
| 本文算法 | 225 | 4 | 98.2 | ||
| GMSD | 344 | 60 | 82.5 | ||
| 图 5(b) | 1109/757 | 无约束MMSD | 80 | 39 | 51.2 |
| 本文算法 | 259 | 24 | 90.7 | ||
| 灰度相关 | 249 | 59 | 76.3 | ||
| 图 5(c) | 728/446 | 无约束MMSD | 245 | 22 | 91.0 |
| 本文算法 | 267 | 21 | 92.1 | ||
| GMSD | 379 | 37 | 90.2 | ||
| 图 5(d) | 839/882 | 无约束MMSD | 242 | 31 | 87.1 |
| 本文算法 | 400 | 14 | 96.5 | ||
图 5(a)影像旋转角度约为45°,左、右影像满足条件的直线数为471、477,GMSD与本文算法匹配得到的直线数目分别为229、225,正确匹配率分别为94.7%、98.2%。
图 5(b)所示两张影像旋转角度约为30°,参考影像、搜索影像上提取直线数目分别为1109、757,GMSD与本文算法匹配得到的直线数目分别为344、259,本文算法同名直线数目少于前者,但错误匹配数目较少,匹配的正确率为90.7%。
图 5(c)为不同光照强度下同一建筑物拍摄获取的影像对,参考影像、搜索影像上提取直线数目分别为728、446,GMSD与本文算法匹配得到的直线数目分别为249、267,正确匹配率分别为76.3%、92.1%。
图 5(d)为同视角同距离不同时间段对同一建筑物区域进行拍摄得到的影像对,参考影像、搜索影像上提取直线数目分别为839、882,GMSD结果中错误匹配直线数目为37,正确匹配率为90.2%,而本文算法匹配数目相对较多,误匹配直线数目为14,正确匹配率为96.5%。上述试验结果表明,基于梯度幅值描述子的可靠性要强于GMSD描述子。
在无约束条件下,利用文献[19]中MMSD算法对上述四组影像进行直线匹配,与上述两种方法相比,该方法匹配得到同名直线数目最少,但是错误直线数目相对较多。这是由于缺乏有效的几何约束,匹配候选较多,导致错误匹配较多,匹配正确率较低。如对于图 5(d)影像,该方法和本文算法匹配得到同名直线的数目分别为242、400,误匹配直线数目分别为31、14,该方法正确率为87.1%,而本文算法在结合三角网和核线约束后,匹配正确率提升至96.5%。
根据表 1可知,在参考影像、搜索影像上直线提取数目相同的情况下,针对上述四组试验影像,相比于GMSD和无约束MMSD匹配方法,本文结合几何约束和梯度幅值描述子的直线匹配算法得到的同名直线数目多,错误少,匹配正确率高。试验结果表明,本文算法具有一定的可靠性。
5 结论针对无约束条件下,基于描述子直线匹配的可靠性问题,本文提出了一种结合几何约束和梯度描述子的直线匹配算法。该方法在已有MMSD描述子基础上,增加三角网约束和核线约束确定匹配候选,减少匹配搜索范围,提高匹配的效率及正确率;同时在描述子构建过程中,分别以目标直线和候选直线对应的重叠段直线为中心建立直线支撑域,并利用高斯卷积函数对支撑域内像素点梯度幅值进行加权处理,提高描述子的有效性及可靠性。通过选择4组不同类型的影像对进行匹配试验,并与无约束MMSD描述子和GMSD描述子两种方法进行对比分析,得出如下结论:与GMSD相比,基于梯度幅值的描述子MMSD适用性及可靠性更强;与无约束MMSD相比,可靠的几何约束不仅提高了直线匹配的效率,同时大大提高了直线匹配的正确率。
| [1] | 王竞雪, 宋伟东, 韩丹, 等. 边缘视差连续性约束的航空影像特征线匹配算法[J]. 信号处理, 2015, 31(3): 364–371. |
| [2] | CHEN M, SHAO Z, LIU C, et al. Scale and Rotation Robust Line-based Matching for High Resolution Images[J]. Optik-International for Light and Electron Optics, 2013, 22(124): 5318–5322. |
| [3] | HAN W, ZHENG J B. Fast and Accurate Stereo Matching Algorithm Based on Epipolar Line Restriction[J]. Computer Engineering & Applications, 2008, 44(1): 51–53. |
| [4] | 朱红, 宋伟东, 杜北, 等. 重合度约束的近景影像直线匹配算法[J]. 信号处理, 2015, 31(8): 912–917. |
| [5] | 吴军, 姚泽鑫, 程门门. 融合SIFT与SGM的倾斜航空影像密集匹配[J]. 遥感学报, 2015, 19(3): 431–442. |
| [6] | 朱庆, 吴波, 赵杰. 基于自适应三角形约束的可靠影像匹配方法[J]. 计算机学报, 2005, 28(10): 1734–1739. DOI:10.3321/j.issn:0254-4164.2005.10.021 |
| [7] | 张云生, 朱庆, 吴波, 等. 一种基于三角网约束的立体影像线特征多级匹配方法[J]. 武汉大学学报(信息科学版), 2013, 38(5): 522–527. |
| [8] | WO B, ZHANG Y S, ZHU Q. Integrated Point and Edge Matching on Poor Textural Images Constrained by Self-adaptive Triangulations[J]. ISPRS Journal of Photogram-metry and Remote Sensing, 2012, 68(1): 40–55. |
| [9] | FAN B, WU F, HU Z. Line Matching Leveraged by Point Correspondences[C]//IEEE Conference on Computer Vision and Pattern Recognition. San Francisco: IEEE, 2010: 390-397. |
| [10] | FAN B, WU F, HU Z. Robust Line Matching through Line Point Invariants[J]. Pattern Recognition, 2012, 45(2): 794–805. DOI:10.1016/j.patcog.2011.08.004 |
| [11] | 陆丽娜. 基于三焦点张量的多视图目标三维重建[D]. 南京: 南京航空航天大学, 2010: 86-88. |
| [12] | 娄安颖, 宋伟东, 刘薇. 基于单应矩阵的直线匹配[J]. 遥感信息, 2011, 15(3): 9–13. |
| [13] | 易成涛, 王孝通, 徐晓刚. 基于极线约束的角点匹配快速算法[J]. 系统仿真学报, 2008, 20(S1): 371–374. |
| [14] | 陈浩, 高志强, 密保秀, 等. 引入极线约束的SURF特征匹配算法[J]. 中国图象图形学报, 2016, 21(8): 1048–1056. DOI:10.11834/jig.20160809 |
| [15] | SCHMID C, ZISSERMAN A. The Geometry and Matching of Lines and Curves over Multiple View[J]. International Journal of Computer Vision, 2000, 40(3): 199–233. |
| [16] | 梁艳, 盛业华, 张卡, 等. 利用局部仿射不变及核线约束的近景影像直线特征匹配[J]. 武汉大学学报(信息科学版), 2014, 39(2): 229–233. |
| [17] | LOWE D G. Distinctive Image Features from Scale-invariant Keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91–110. DOI:10.1023/B:VISI.0000029664.99615.94 |
| [18] | 缪君, 储珺, 张桂梅. 一种仿射不变的直线描述子与直线匹配[J]. 电子学报, 2015, 43(12): 2505–2512. DOI:10.3969/j.issn.0372-2112.2015.12.024 |
| [19] | 王志衡, 吴福朝. 均值-标准差描述子与直线匹配[J]. 模式识别与人工智能, 2009, 22(1): 32–39. |


