2. 武汉大学遥感信息工程学院, 湖北 武汉 430079
2. School of Remote Sensing and Information Engineering, Wuhan University, Wuhan 430079, China
卫星钟差的预报精度将对卫星星历的预报精度及卫星的自主导航能力产生较大的影响[1]。关于钟差的预报模型研究,国内外作了许多研究。目前研究较为成熟的钟差预报模型主要包括:多项式模型[2-3]、灰色模型[4]、神经网络[5]等方法。二次多项式模型顾及卫星钟差的物理特性,是目前广播星历中广泛采用的钟差外推方法,但是二次多项式在卫星钟差的长期预报中误差累计较快,极易产生较大的偏差;灰色模型只需较少的试验数据即可建立预报模型,崔先强等最早提出利用灰色模型对卫星钟差进行预报[4],并且分析了二次多项式模型在长期预报中的缺陷,研究发现灰色模型在短期预报中与二次多项式精度相当,但是在长期预报中其预报精度明显优于二次多项式模型;文献[6]指出一个复杂的、非线性、非平稳变化的时间序列很难用单一模型进行有效的预报;卫星钟极易受外界环境和自身因素的影响,因此钟差灰色模型无法取得较好的结果;神经网络模型是基于风险最小原理建立的,易陷于局部最小和网络结构难以构建等问题,从而导致学习过度的情况出现;基于此,雷雨等[7]采用基于经验模态分解(empirical mode decomposition, EMD)和最小二乘支持向量机(least squares support vector machine, LSSVM)相结合的钟差预报方法,预报结果明显高于二次多项式模型、灰色模型和单一的LSSVM模型。
由于EMD中存在模态混淆的问题[8-9],本文集合经验模态分解(ensemble empirical mode decomposition, EEMD)进行残差的分解,构建一种高精度的组合钟差预报模型。文中采用iGMAS官网发布的超快速钟差产品进行试验和结果分析,首先针对iGMAS发布的北斗卫星钟差进行稳定性分析,针对分析结果提出该组合预报模型;之后采用IGS发布的GPS卫星钟差数据预报,验证该模型的正确性;最后将该模型应用到北斗卫星钟差中。
1 预报模型EEMD的本质是对一个信号进行平稳化处理,其结果是将一个非平稳的时间序列分解成一系列较为平稳的时间序列,这种方法能够有效地处理非平稳、非线性的时间序列,已有较为详细的叙述[9],在此不再赘述。
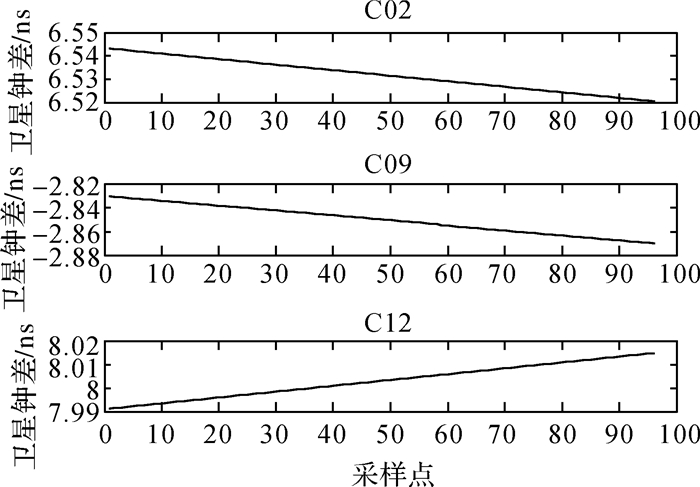
为更为直观地分析原始钟差时间序列和去除趋势项后残差序列的特征,以及EEMD对残差序列的分解效果,从国际GNSS监测评估系统(International GNSS Monitoring & Assessment System,iGMAS)下载2016年年积日303该天数据(采样间隔15 min),其原始数据变化趋势及残差分解效果如图 1、图 2所示。
|
| 图 1 钟差原始数据 |
|
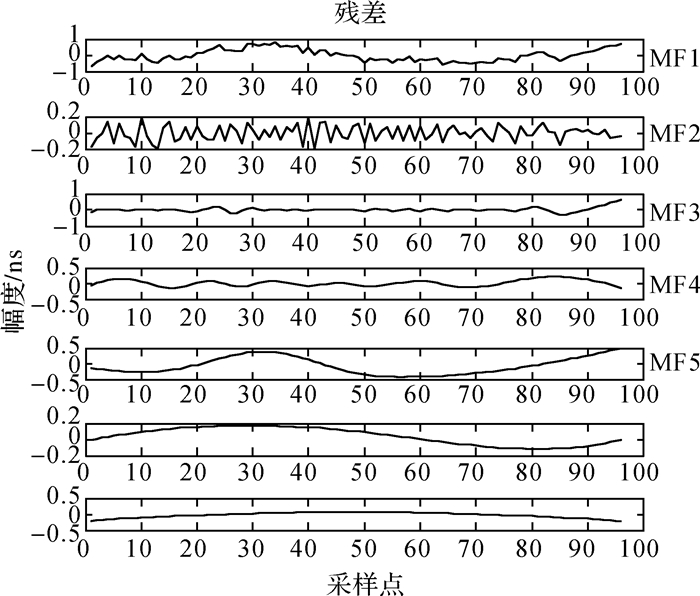
| 图 2 EEMD分解结果 |
图 1为原子钟的原始时间序列,从图中可以看出卫星钟差存在一定的趋势项,扣除趋势项后的时间序列是一个非平稳、非线性的时间序列(如图 2中残差),无法采用单一的预报模型进行准确预报,而EEMD方法能够将一个非平稳的时间序列分解成若干较为平稳的时间序列(如图 2中残差MF1—MF5)和一个余项。基于此,将EEMD方法引入北斗卫星钟差预报模型中,构成组合预报模型。
本文主要根据EEMD分解后得到的时间序列的特征, 考虑各模型的优缺点,选择合适的比例因子将灰色模型[12](gray forecast model, GM)、最小二乘支持向量机[13]、自回归模型(autoregressive model, AR)、多项式模型(quadratic polynomial, QP)的模型预报值进行线性组合以确定最终预报值。本文所构建组合预报模型具体公式如下,式中GM、QP、AR、LSSVM分别表示各模型的预报值
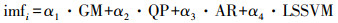 (1)
(1) 式中,imfi为模态IMF的预报值;[α1 α2 α3 α4]为比例因子。
关于比例因子的确定,采用抗差最小二乘方法进行估计。选择平均值作为初始值,Δtim为第i个历元第m个预报模型的预报值
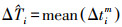 (2)
(2) 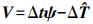 (3)
(3) 式中
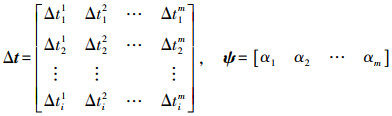 (4)
(4) 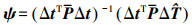 (5)
(5) 以IGG-Ⅲ作为迭代函数[14],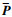
根据比例因子确定单个时间序列的预测值,之后对各时间序列的预报值进行重构,得到最终钟差预报值ΔT(j), j=N+1, N+2, …, N+P,其中P表示预报历元的个数。ΔT(j)的表达式为
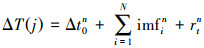 (6)
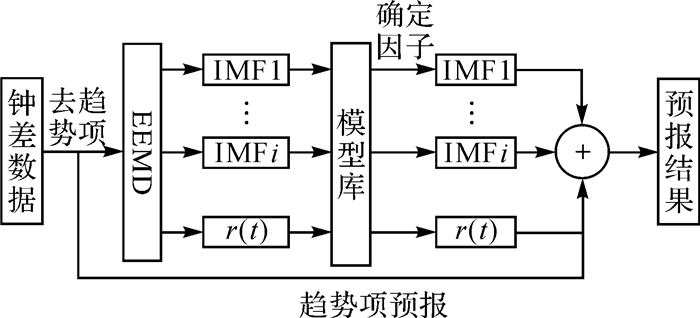
(6) 式中,Δt0n为趋势项第n预报值;imfin为第i时间序列第n预报值;rtn为剩余项第n预报值。本文所提组合钟差预报算法的流程如图 3所示。
|
| 图 3 钟差预报流程 |
卫星钟差数据用于定位时当系统性偏差小于2.5×10-7 s时,系统误差将被接收机钟差吸收[15],对定位结果影响不大。因此在进行卫星钟差精度分析时采用标准差表示钟差预报精度更具有现实意义。在精度评定时以最终的钟差产品作为真值,采用二次差的方法进行卫星钟差的预报精度分析[1]。
2.1 GPS卫星钟预报分析该小节选用国际GNSS服务组织(The International GNSS Service,IGS)发布的GPS卫星钟差数据进行预报试验。选取GPS周第1932周,一周的igu产品,采用一天数据建模预报接下来24 h的卫星钟差,预报精度与igu预报部分精度进行比较。选择铷钟PRN01、06,铯钟PRN09、10共4颗GPS卫星进行预报分析,试验结果见图 4—图 7及表 1。
|
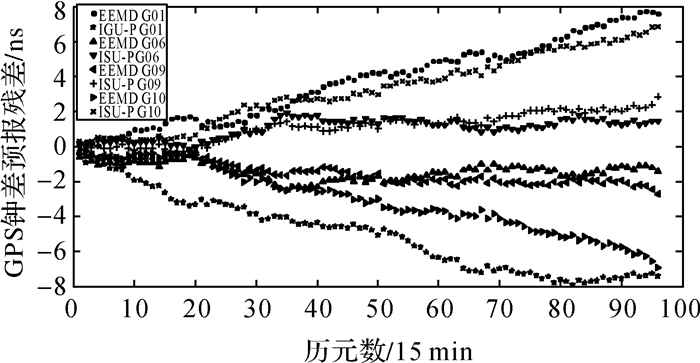
| 图 4 GPS卫星钟24 h预报残差 |
|
| 图 5 GPS卫星钟24 h预报精度 |
|
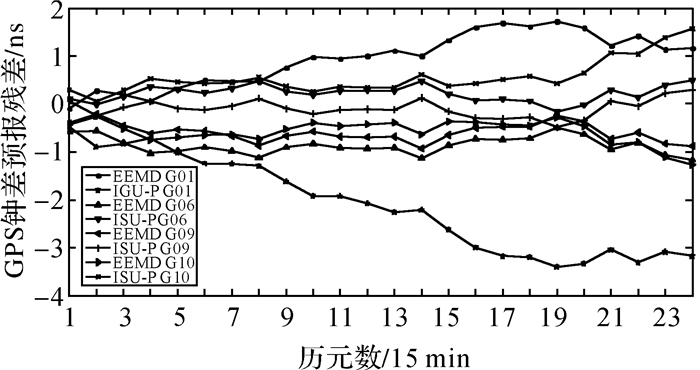
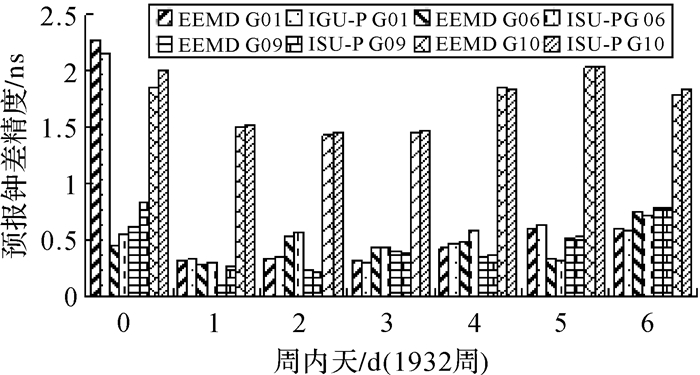
| 图 6 GPS卫星钟6 h预报残差 |
|
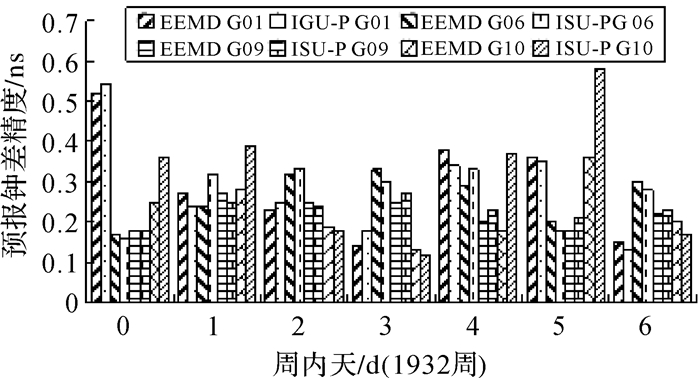
| 图 7 GPS卫星钟6 h预报精度 |
| ns | |||||||||
| 方法 | 24 h | 6 h | |||||||
| G01 | G06 | G09 | G10 | G01 | G06 | G09 | G10 | ||
| IGU-P | 0.69 | 0.50 | 0.48 | 1.73 | 0.29 | 0.26 | 0.22 | 0.31 | |
| EEMD | 0.68 | 0.47 | 0.42 | 1.70 | 0.29 | 0.25 | 0.23 | 0.23 | |
| Raise | 1.4% | 6% | 12.5% | 1.7% | 0% | 3.8% | -4.5% | 25.8% | |
图 4—图 7为采用本文算法进行预报的钟差结果与IGS发布的超快速卫星钟差预报部分之间的比较,24 h、6 h预报精度最高分别提高了12.5%、25.8%。对比结果表明,24 h预报精度较6 h的预报精度明显提高;另外铯钟的预报精度要比铷钟的预报精度高。试验分析表明本文所提出的钟差预报算法对GPS钟差预报精度与IGU预报部分精度相当。我国北斗导航系统同样搭载着高精度的铷原子钟,因此本文所提算法也应适用于北斗卫星钟差。下面将详细介绍本文所提算法在BDS卫星钟差预报中的应用。
2.2 BDS卫星钟预报分析为了充分分析本文所提钟差预报模型的效果,选取iGMAS发布的2016年年积日为303至332共30天的超快速(ISU)钟差数据作为试验数据。分别从GEO、IGSO、MEO这3类卫星中各选取卫星一颗(C03、C09、C12)进行试验,同样与iGMAS公布的超快速产品预报部分精度进行对比。采用1天数据进行建模数据预报后面6、12和24 h的钟差。预报结果如图 8—图 13和表2所示。
|
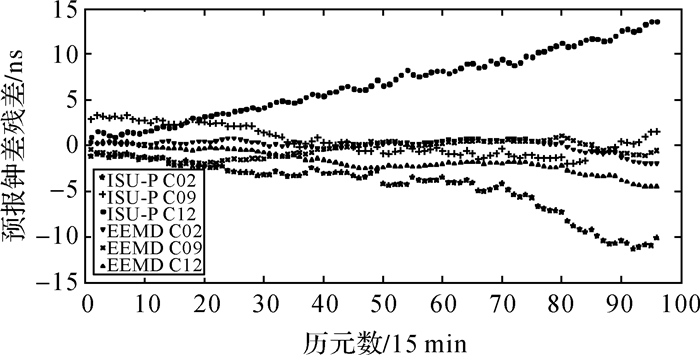
| 图 8 BDS卫星钟24 h预报残差 |
|
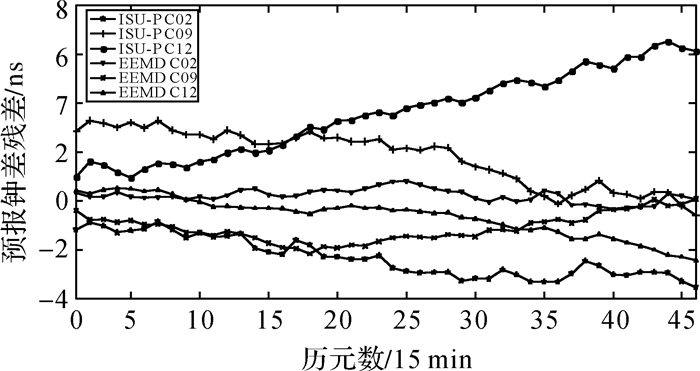
| 图 9 BDS卫星钟12 h预报残差 |
|
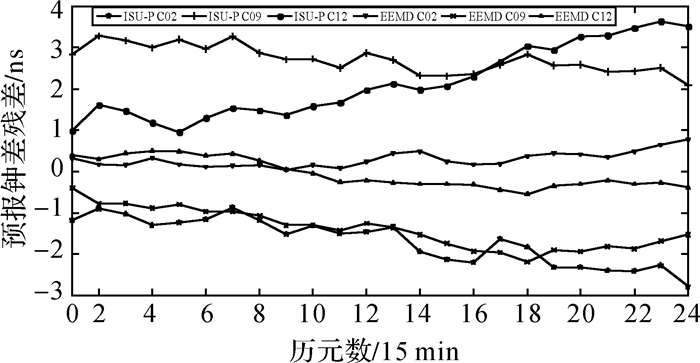
| 图 10 BDS卫星钟6 h预报残差 |
|
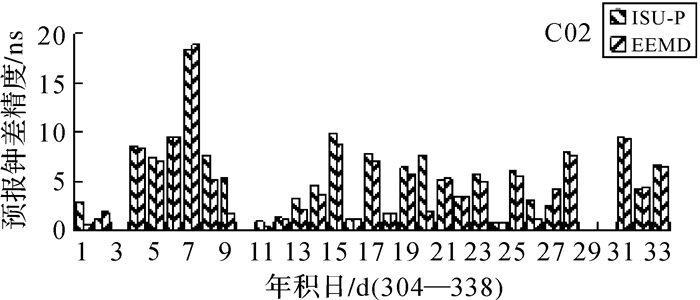
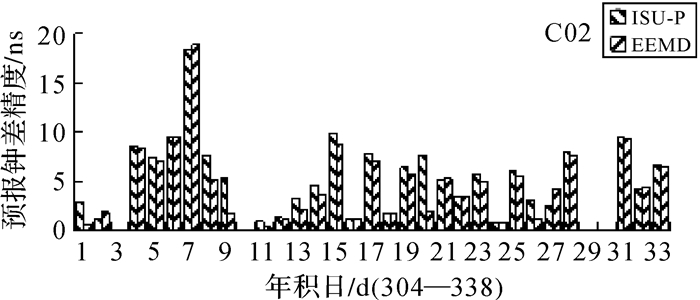
| 图 11 C02卫星24预报残差精度统计 |
|
| 图 12 C09卫星12预报残差精度统计 |
|
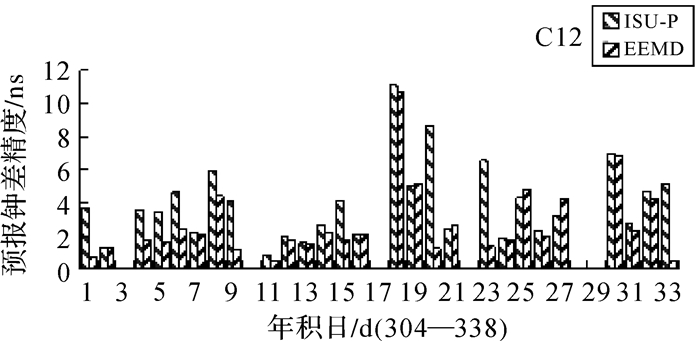
| 图 13 C12卫星6预报残差精度统计 |
图 8—图 13表示北斗卫星钟差24 h、12 h和6 h钟差预报残差与ISU-P残差的对照图,图15-图17和表 3表示C02、C09、C12卫星预报残差统计。通过一天数据进行建模分析,本文所提算法相对于ISU-P预报精度有较大提高,24 h预报精度分别提升了31.1%、30.7%、26%,12 h预报精度分别提升了43%、23%、21.8%,6 h预报精度分别提升了13.3%、7.3%、31.8%。星钟差随着预报时间的增加,ISU-P存在着明显的漂移,误差累计较快,而本文所采用的钟差预报方法误差累积较慢,取得了较好的结果。MEO卫星钟差的预报精度相对于GEO和IGSO卫星钟精度较好,也反映出MEO卫星钟较为稳定,与上文中所做稳定性分析相符。在所选择33天的试验数据中,有些天预报精度较差是由于数据质量不好无法进行准确模态分解导致的。
| ns | |||||||||||
| 方法 | 6 h | 12 h | 24 h | ||||||||
| C02 | C09 | C12 | C02 | C09 | C12 | C02 | C09 | C12 | |||
| ISU-P | 1.86 | 1.63 | 0.96 | 3.93 | 2.03 | 1.93 | 5.55 | 4.25 | 3.96 | ||
| EEMD | 1.28 | 1.13 | 0.71 | 2.24 | 1.65 | 1.51 | 4.81 | 3.94 | 2.70 | ||
| Raise | 31.1% | 30.7% | 26.0% | 43.0% | 23.0% | 21.8% | 13.3% | 7.3% | 31.8% | ||
本文为提高北斗卫星钟差预报精度,提出联合多项式和EEMD模型构建组合钟差预报模型,首先采用IGS发布的GPS钟差数据验证本文所提预报模型的正确性,之后对BDS卫星钟差进行预报。采用所提钟差预报模型对GPS卫星钟差进行预报,得到的钟差预报结果与IGS发布的IGU-P部分进行对比分析,24 h和6 h钟差预报精度相对于IGS预报部分分别提高了1.4%、6%、12.5%、1.7%和0%、3.4%、-4.5%、25.8%,充分说明了该算法对钟差预报的有效性;最后将本文所提算法应用于BDS卫星钟差预报,采用1 d数据进行建模预报接下来6、12、24 h的钟差,试验结果表明6、12、24 h较iGMAS北斗卫星钟差超快速预报部分提高幅度分别为26.0%~31.1%、21.8%~43.0%、7.3%~31.8%。本文所提算法具有较高的稳定性,能够较大幅度提高北斗卫星钟差的预报精度。
致谢: 感谢国际GNSS监测评估系统(iGMAS)提供的数据。| [1] | 黄观文. GNSS星载原子钟质量评价及精密钟差算法研究[D]. 西安: 长安大学, 2012. |
| [2] | KOSAKA M. Evaluation Method of Polynomial Models' Prediction Performance for Random Clock Error[J]. Journal of Guidance Control & Dynamics, 1987, 10(6): 523–527. |
| [3] | 王甫红, 夏博洋, 龚学文. 顾及钟差变化率的GPS卫星钟差预报法[J]. 测绘学报, 2016, 45(12): 1387–1395. DOI:10.11947/j.AGCS.2016.20150480 |
| [4] | 崔先强, 焦文海. 灰色系统模型在卫星钟差预报中的应用[J]. 武汉大学学报(信息科学版), 2005, 30(5): 447–450. |
| [5] | 梁月吉, 任超, 杨秀发, 等. 结合双树复小波和广义回归神经网络的钟差预报方法研究[J]. 测绘通报, 2016(1): 6–10. |
| [6] | HUANG N E, WU M, QU W, et al. Application of Hilbert-Huang Transform to Non-stationary Financial Time Series Analysis[J]. Applied Stochastic Models in Business & Industry, 2003, 19(3): 245–268. |
| [7] | 雷雨, 赵丹宁. 基于经验模式分解和最小二乘支持向量机的卫星钟差预报[J]. 天文学报, 2014, 55(3): 216–227. |
| [8] | ZHENG J, CHENG J, YANG Y. Partly Ensemble Empirical Mode Decomposition:An Improved Noise-assisted Method for Eliminating Mode Mixing[J]. Signal Processing, 2014, 96: 362–374. DOI:10.1016/j.sigpro.2013.09.013 |
| [9] | LEI Y, HE Z, ZI Y. EEMD Method and WNN for Fault Diagnosis of Locomotive Roller Bearings[J]. Expert Systems with Applications, 2011, 38(6): 7334–7341. DOI:10.1016/j.eswa.2010.12.095 |
| [10] | 付文举. GNSS在轨卫星钟特性分析及钟差预报研究[D]. 西安: 长安大学, 2014. |
| [11] | 孟繁林. 集合经验模态分解的理论及应用研究[D]. 镇江: 江苏科技大学, 2013. |
| [12] | 邓聚龙. 灰色控制系统[J]. 华中科技大学学报(自然科学版), 1982(3): 11–20. |
| [13] | BRABANTER K D, KARSMAKERS P, OJEDA F, et al. LS-SVMlab Toolbox User's Guide:Version 1.7[J]. Ku Leuven Leuven, 2011, 66(8): 6–9. |
| [14] | 李浩军, 唐诗华, 黄杰. 经典选权迭代法研究与两步抗差估计的提出[J]. 海洋测绘, 2007, 27(1): 17–20. |
| [15] | 于合理, 郝金明, 宋超, 等. 卫星钟系统偏差对精密单点定位精度的影响[J]. 测绘科学技术学报, 2013, 30(2): 136–139. |


