时间频率传递是指借助一定媒介实现标准时间频率信号从源到终端的传输,使多个节点同一个公用精确参考时间/频率之间完成远距离时间/频率比对。精密时间频率传递技术是现代社会中应用最广泛的技术之一,其应用领域包括科学观测及研究、定位及导航业务、通信、电网、交通、金融、紧急救援、环境资源管理等,并且目前还在不断扩展。同时,精密时间频率传递技术也是协调世界时UTC(coordinated universal time)、国际原子时TAI(international atomic time)等国际时间标准建立和维持的支撑技术之一。国际时间尺度的建立,其实际的性能瓶颈并不在于钟,而在于两地间时间频率信息传递的精度[1]。
当前主流的远距离精密时间频率传递技术有卫星时频传递、光纤时频传递及激光时间传递。自20世纪80年代起,GNSS(global navigation satellite systems)测量便被用于高精度、高准确度时间频率传递。GNSS时频传递的主要方法有两种:一是精密单点定位(precise point positioning,PPP),该方法利用单站非差测量值确定接收机时钟与系统时之间的同步误差[1-6];二是共视法(common view,CV),该方法基于单差分析结果以获得两个观测站主钟之间的同步误差[7-8]。除GNSS时频传递技术之外,卫星双向时频传递(two-way satellite time and frequency transfer,TWSTFT)是另一种重要的时频传递技术,也是目前最精确的远距离时间频率比对方法之一。该方法中,两观测站经GEO(geostationary earth orbit)卫星对发定时信号,两站分别测量定时信号传播时延并事后交换数据,可计算出两站主钟之间的同步误差[9]。
随着光纤的大面积铺设,目前其已成为一种极具前景的时间频率信号传输媒介。不同地域实验室的频率标准可通过光纤网络传输的参考光载波实现比对(通常采用光梳技术)和同步;通过光强调制将时间频率电信号转换为光信号,在接收端进行直接光强探测,将光信号再转换为电信号,这是光纤时频传递的第二种模式;第三种模式是将光信号相位锁定到超稳钛蓝光频率参考基准,可获得与高稳无调制光载波传输模式相比拟的频率传递精度,同时提供了与时间频率电信号进行直接比对的接口[10-12]。
激光时间传递技术包括激光时间传递(laser time transfer,LTT)和基于激光链路的时间传递(time transfer by laser link,T2L2),两者均源自卫星激光测距(satellite laser range,SLR)技术。LTT能够校准以GNSS系统为代表的伪码调制微波时间传递系统,评估星载钟的短期性能,提升星载钟的预测精度;T2L2利用ILRS(international laser ranging service)网络,可实现超稳远距离地面钟之间的时间传递与比对[13-15]。
远距离时钟比对及稳定精确授时对于人类未来在空间和地面的诸多行为(导航、宽带通信网络及基础科学研究等)具有深远的影响。因此,有必要在效率、精度、准确度及安全性等方面进一步推动时间频率传递技术的发展。
1 卫星时频传递技术 1.1 GNSS时频传递技术GNSS时频传递技术指依托GNSS系统及其精密测距理论实现时间、频率传递的技术。该技术具有覆盖范围广、精度高的特点,可满足不同领域、不同精度等级的应用需求,是目前应用最广泛的时频传递技术。
任一地面站观测GNSS卫星s的载波相位测量方程及伪距测量方程分别为
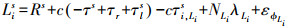 (1)
(1) 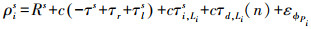 (2)
(2) 式中,Rs为接收机与卫星之间的几何距离;τs为卫星钟差;τr为接收机钟差;τls为对流层时延;τis为电离层时延;λLi为载波波长;N为相位模糊度;ε为噪声;τd(n)为相应于频率Li和通道n的未经校准的接收机硬件时延。
PPP时频传递技术在式(1)和式(2)基础上,联立求解消除电离层时延,并借助IGS(International GNSS Service)提供的精密卫星轨道数据及星载钟时间序列(以IGS时间为参考基准),可确定GNSS天线相位中心位置、对流层湿分量顶点路径时延及接收机时钟与相应的卫星导航系统时之间的同步误差。时间传递精度通常情况下可达几个纳秒,理想情况下小于100皮秒(ps),日频率稳定度可达10-14~10-15。
PPP时频传递技术本质上是一种单站后处理技术。2009年9月,该技术以其高稳定性被BIPM(Bureau International de Poids et de Mesures)正式采纳,参与TAI计算。相比于其他卫星时频传递技术,PPP时频传递的优势在于精度高、设备成本低、无基线长度限制。不足在于实时性差,不适用于本地钟性能的实时监测。PPP时频传递的另一点不足是边界(日、周)不连续性,该不连续性是由伪距观测量中的有色噪声(源于近场多径效应或设备时延变化)引起的,该有色噪声带来的误差并不能通过PPP观测模型进行有效的补偿。
不同于PPP法,卫星共视时频传递需要构造不同测站对同一卫星的同步观测值的差,即构造式(1)与式(2)的单差。共视时频传递同样被BIPM采纳并用于TAI产生。该技术的优点是卫星位置及星载钟残差可大幅度降低,其时间传递精度在1~10 ns范围内变化,日频率稳定度为1×10-14。该方法的缺点是两测站事后数据交换及处理会带来一定的时间延迟,因而不适用于实时业务;共视卫星的数目要少于观测站可观测到的卫星数目,从而造成分析过程中有效数据的减少。此外,该方法的传递精度受基线长度影响。当采用码和载波相位联合分析时,基线长度应限制在2000 km之内[5]。中间站可用于解决两目标测站距离较远的问题,且能够获得近似于短基线时频传递的同步精度。
1.2 卫星双向时频传递技术双向传递是另一种重要的卫星时频传递技术,被广泛应用于TAI的建立与维持。该技术的基本工作原理是两测站在约定历元产生时间信号,并且经由GEO(geostationary earth orbit)卫星转发给对方测站,同时测量本站时间信号产生历元与接收并恢复出对方测站时间信号的历元时刻之间的时间间隔。两站测量的时间间隔T1和T2分别为
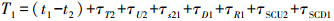 (3)
(3) 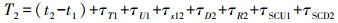 (4)
(4) 式中,t1、t2分别为两站主钟钟面时;τT1、τT2分别为两站时间信号发射时延;τR1、τR2分别为两站时间信号接收时延;τU1、τU2分别为两站时间信号从天线到GEO卫星的上行传播时延;τs12、τs21分别为GEO卫星对站1、站2时间信号的转发时延;τD1、τD2分别为时间信号从GEO卫星到站1和站2的下行传播时延;τSCU1、τSCU2分别为两站上行信号的Sagnac校正;τSCD1、τSCD2分别为两站下行信号的Sagnac校正。
两站通过事后数据交换及处理,可得到两站钟差。卫星双向时频传递的优点是利用信号双向传播的良好对称性,实现了高精度传递:时间传递精度小于1 ns,日频率稳定度约为10-15。该技术的局限性在于GEO卫星资源有限,两站之间通常采用单星、单链路进行时频比对。如在条件许可的情况下,基于多星(N颗)、多链路动态加权平均的双向时频传递,时间传递精度可提升
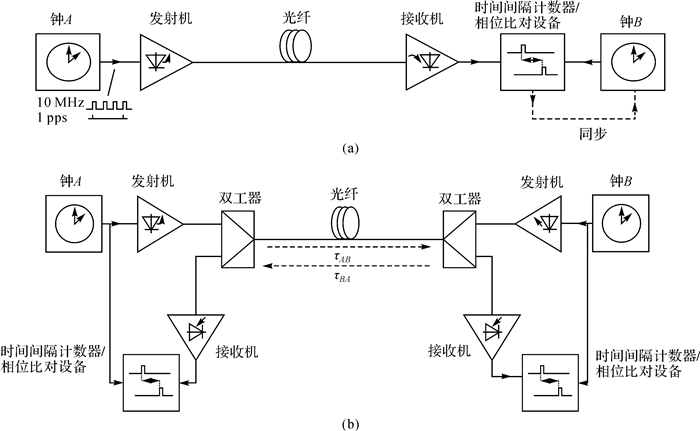
光纤时频传递具有单向、双向两种模式。单向模式如图 1(a)所示。钟A产生的时频信号(时间信号通常为1PPS(秒脉冲),频率信号通常为10 MHz正弦/方波信号)经过光强度调制转换为光信号之后,通过光纤进行传输(也可根据实际需要,附加编码等操作,再送入光纤)。接收端的信号再次转换为电信号格式,经放大和整形后,通过时间间隔计数器/鉴相器与本地钟B的时间/频率信号进行比对,即可得到本地钟B与远距离钟A的钟差和频率差。该传递方式需确定信号在光纤中的传播时延。通常情况下,该时延是比较容易确定的,但是该传递方式的精度将受到光纤温度变化等非理想因素带来的时延不稳定性的限制[10-11]。
|
| 图 1 光纤时频传递示意图 |
由于单向模式在光信号传输时延不确定性方面的局限,要获得更高的传递精度,需采用双向光纤时频传递技术,其基本架构如图 1(b)所示。双向模式基本工作原理与TWSTFT类似,甲、乙两站主钟A和B通过同一光纤在约定时刻对发时间信号,并借助时间间隔计数器测量本地时间信号产生直至接收到对方时间信号之间的时间间隔。甲、乙两站测量的时间间隔分别为
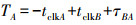 (5)
(5) 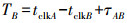 (6)
(6) 式中,τBA、τAB分别为两个方向的光纤传输时延。为了简化表达式,发射机、接收机处理时延及光纤两端双工器时延未予以体现,实际中需精确标定。
两站事后交换测量数据,可计算出A、B两钟钟差。单向光纤时频传递精度受光纤传输时延热相关性影响较大,约为38 ps(K·km)-1[10]。因此,当光纤长度在几千米之内时,可获得较理想的传递精度。双向光纤时频传递精度受限于残余时延失配的温度相关性,大致在1.5×10-3~4.5×10-3(nm·km·K)-1的范围内[10]。因此,相比于单向模式,双向模式降低了光纤温度变化的影响。
光纤时频传递的优势在于具有较高的传递精度。但也存在两点局限:一是光纤长度(覆盖范围)。当光纤长度超过几百公里时,路径损耗及光纤噪声等问题凸显,信噪比严重下降,精度难以保证。该问题可通过增加双向光纤放大器及增加中继站的方式解决。二是高成本。目前光纤时频传递需要布设专用光纤,费用昂贵。有文献提出可利用现有公共电信网络进行时频传递,即高稳光时频信号和普通电信数据共用一根光纤进行传输。其基本思路是利用密集波分复用(dense wavelength division multiplexing,DWDM)技术。该技术将光纤传输总带宽分为若干等间隔的信道,选择其中一个信道进行时频信号传递,其余信道进行数据传输。结合中继站和密集波分复用技术,采用总长为540 km的光纤链路在两个时间实验室之间进行频率传递,端到端频偏均值为-2.6×10-20,长期频率稳定度为1×10-19[12],该频率稳定度和精度水平可比拟无中继专用光纤链路,该试验初步验证了公共电信网络具备用于超稳、高精度频率传递的实际可行性。
3 激光时间传递技术星地激光时间传递(LTT)的原理为:地面站向卫星发射激光脉冲,该脉冲到达卫星后,经星上反射器反射,再返回地面站。地面站测量发送激光脉冲与其后第一个地面站主钟秒脉冲之间的时间间隔;星载设备测量激光脉冲到达卫星时刻与前一个星载钟秒脉冲之间的时间间隔;激光脉冲上行传播时延根据地面站测量的往返时延得到,进而求出星载钟与地面站主钟之间的钟差[13-14]。该技术的时间传递精度约为300 ps,频率稳定度可达3×10-14(2000 s)[13-14],比基于微波的时频传递技术在精度上至少高了一个数量级。既可用于电离层时延校正,也可用于提升卫星轨道预测的精度和准确度,同时可增强系统在星载钟比对、监测及校准方面的能力。考虑该技术在实际工程应用中需设计构建专门的测量系统,专业性较强,因此该传递方法的研究、试验和推广需依靠有条件的组织、院校或研发机构开展。
基于激光链路工程的时间传递(T2L2)的基本原理与LTT类似,LTT技术目前主要与卫星导航系统结合应用,而T2L2技术基于2008年6月发射的Jason-2卫星(轨道高度1335 km)。相比于LTT,该技术所基于的卫星轨道更低,从而使得到达卫星的光信号密度更强。该技术的时间传递精度优于100 ps,通常在50~70 ps左右,时间稳定程度约为7 ps(30 s),该值受限于T2L2星载晶体振荡器的稳定程度[15]。基于该技术,两个地面站之间还可进行共视时间传递,共视原理近似于前文所述的卫星共视时频传递技术。采用单链路T2L2共视技术,短期时间稳定度约为9~11 ps;采用多链路加权平均T2L2共视技术,日时间稳定度可达10 ps[15]。
激光时间传递技术原理简单、传递精度和稳定度高,但其应用领域还有待进一步拓展。星载高精度激光探测技术、星载计数器、地面站激光发射时间控制、数据处理等为激光时间传递的关键环节,这些环节的技术突破可带来激光时间传递精度和稳定度的新提升。
4 结论本文对3类主流的精密时频传递技术进行了研究。卫星时频传递应用范围广、精度高,是目前最主要的时频传递技术。该技术未来的发展趋势是多系统融合,增加可用卫星的数量及采用更先进的数据处理方法。挑战是安全性、可靠性及对复杂、恶劣环境的适应性。光纤时频传递将精密时间频率信号转换为超稳光信号,采用有线方式(光纤)进行传输,受环境影响较小,各误差项可得到有效测量和补偿,精度和稳定度高。目前主要用于中、短距离时间实验室之间的高精度时频比对,具有良好的发展前景。该技术未来的研究热点包括:光纤热敏感性、色散特性、相噪特性及其抑制方法;中继站研究与设计;光纤链路附属精密双向设备/装置研制;广域光纤时频传递网络部署研究。面临的挑战是部署灵活性、时频信号完好性及与现有电信网的融合。激光时间传递技术利用激光的直线传输特性,获得比微波更精确的星地信号传播时延测量值,从而实现星载钟与地面站主钟的高精度、高稳定性时间比对。由于该技术实施需要专用系统及设备,应用领域有限,目前主要的应用方向是与卫星导航系统结合,作为附加精密时钟源,提升其系统性能。该技术未来可在以下方面进行重点研究和探索:多系统融合应用;星地激光传输关键技术研究及专业设备研制;激光时间传递系统通用接口设计及标准化;授时性能监测(精确性、完好性)。以上技术的研究,可为我国正在进行的国家时频体系建设提供参考。例如,在一级时间实验室的选址及建设过程中,需考虑以上3类时频传递技术的综合应用,以保证一级时间实验室之间时频信号比对的高精度、高稳定性、高可靠性和高安全性(日常/战时)。
| [1] | DEFRAIGNE P, BAIRE Q. Combining GPS and GLONASS for Time and Frequency Transfer[J]. Advances in Space Research, 2011, 47(2): 265–275. DOI:10.1016/j.asr.2010.07.003 |
| [2] | LAHAYE F, CERRETTO G, TAVELLA P. GNSS Geodetic Techniques for Time and Frequency Transfer Applications[J]. Advances in Space Research, 2011, 47(2): 253–264. DOI:10.1016/j.asr.2010.05.032 |
| [3] | JIANG Z. Accurate Time Link Calibration for UTC Time Transfer-Status of the BIPM Pilot Study on the UTC Time Link Calibration[C]//European Frequency & Time Forum & International Frequency Control Symposium. [S. l. ]: IEEE, 2014: 483-486. |
| [4] | LEJBA P, NAWROCKI J, LEMANSKI D, et al. Precise Point Positioning Technique for Short and Long Baselines Time Transfer[C]//European Frequency & Time Forum & International Frequency Control Symposium. [S. l. ]: IEEE, 2013: 815-818. |
| [5] | DEFRAIGNE P, BAIRE Q, LAHAYE F, et al. Near Real-time Comparison of UTC(k)'s through a Precise Point Positioning Approach[C]//European Frequency & Time Forum & International Frequency Control Symposium. [S. l. ]: IEEE, 2012: 349-353. |
| [6] | KUANG C L, LIU J N, HOU F. Time Transfer Based on GPS Precise Point Positioning[C]//International Conference on Signal Processing. [S. l. ]: 知网, 2006. |
| [7] | XU L, LI X, XUE Y. A New Timing Method Based on Common-view[C]//IEEE International Frequency Control Symposium & Exposition. [S. l. ]: IEEE, 2012. |
| [8] | WEISS M A, PETIT G, JIANG Z. A Comparison of GPS Common-view Time Transfer to All-in-View[C]//IEEE International Frequency Control Symposium & Exposition. [S. l. ]: IEEE, 2005: 324-328. |
| [9] | YANG W K, GONG H, LIU Z J, et al. Improved Two-way Satellite Time and Frequency Transfer with Multi-GEO in BeiDou Navigation System[J]. Sci China Inf Sci, 2014, 57(15): 1–15. |
| [10] | ŚLIWCZYŃSKI1Ĺ, KREHLIK P, LIPIŃSKI M. Optical Fibers in Time and Frequency Transfer[J]. Measurement Science and Technology, 2010, 21(7): 1–11. |
| [11] | KODET J, PÁNEK P, PROCHÁZKA I. Two-way Time Transfer via Optical Fiber Providing Subpicosecond Precision and High Temperature Stability[J]. Metrologia, 2016, 53(1): 18–26. DOI:10.1088/0026-1394/53/1/18 |
| [12] | LOPEZ O, KÉFÉLIAN F, JIANG H F. Frequency and Time Transfer for Metrology and Beyond Using Telecommunication Network Fibres[J]. Comptes Rendus Physique, 2015, 16(5): 531–539. DOI:10.1016/j.crhy.2015.04.005 |
| [13] | MENG W D, ZHANG H F, HUANG P C, et al. Design and Experiment of Onboard Laser Time Transfer in Chinese Beidou Navigation Satellites[J]. Advances in Space Research, 2013, 51(6): 951–958. DOI:10.1016/j.asr.2012.08.007 |
| [14] | PROCHAZKA I, SCHREIBER U, SCHAFER W. Laser Time Transfer and Its Application in the Galileo Programme[J]. Advances in Space Research, 2011, 47: 239–246. DOI:10.1016/j.asr.2010.02.008 |
| [15] | EXERTIER P, SAMAIN E, MARTIN N, et al. Time Transfer by Laser Link:Data Analysis and Validation to the ps Level[J]. Advances in Space Research, 2014, 54(11): 2371–2385. DOI:10.1016/j.asr.2014.08.015 |
| [16] | 于合理, 郝金明, 刘伟平, 等. 附加原子钟物理模型的PPP时间传递算法[J]. 测绘学报, 2016, 45(11): 1285–1292. DOI:10.11947/j.AGCS.2016.20160217 |
| [17] | 荆文芳, 卢晓春, 刘枫, 等. 卫星双向载波相位时间频率传递及其误差分析[J]. 测绘学报, 2014, 43(11): 1118–1126. |
| [18] | 肖进丽, 潘正风, 黄声享. GPS/INS组合导航系统时间同步方法研究[J]. 测绘通报, 2007(4): 27–29. |


