2. 南京信息工程大学地理与 遥感学院, 江苏 南京 210044
2. School of Geography and Remote Sensing, Nanjing University of Information Science & Technology, Nanjing 210044, China
卫星影像几何定位仿真研究是开展航天遥感论证、几何质量评价和误差理论分析等工作中的一个重要环节。近几年我国重点发展高分辨率卫星开展测绘工作, 使得该项研究工作受到更多研究学者的关注。其中, 卫星传感器严格几何成像模型及外检校方法是几何定位仿真的理论基础, 也是目前该领域的研究热点之一。如祝小勇等在建立了CBERS-02B卫星影像严格成像几何模型后, 分析了在进行外检校时, 俯仰、滚动和偏航角度对影像几何定位精度的影响[1]。袁修孝等在原有的研究基础上, 提出了更为严密的影像姿态角系统误差检校方法, 并且利用SPOT 5和CBERS-02B卫星影像进行了试验验证[2]。李奇峻等针对ZY-3卫星多光谱相机特点, 提出了运用罗德里格矩阵建立姿态角常差检校方法, 并且利用大连地区ZY-3影像进行了算法检验[3]。孟伟灿等以天绘一号卫星高分相机为例, 在构建其严格成像模型后, 提出了内外部误差补偿模型, 并且设计了5组试验检验补偿效果[4]。杨博等在建立资源一号02C卫星全色影像严格几何成像模型后, 采用分步迭代方法计算内外检校参数, 并且利用嵩山定标场参考数据对检校结果进行评价[5]。牛常领等在对ZY-3卫星影像姿态角检验时, 对比分析了利用四元数和姿态角两种误差补偿模型所取得的精度[6]。
GF-4卫星作为我国高分辨率对地观测系统中的一颗静止轨道卫星, 已于2015年12月29日在西昌卫星发射中心成功发射[7-8]。该卫星采用面阵成像方式获取高时间分辨率(重访周期20 s)、大幅宽(可见光近红外通道/中波红外通道幅宽约500 km/400 km)卫星影像, 并且凭借其灵活机动(5种成像模式——凝视模式、跟踪模式、巡航模式、签到模式、夜间模式)的特点, 已经为我国灾害监测、气象预报、环境保护等领域提供了有效的数据支持[9-10]。同样, 对于该静止面阵成像卫星而言, 也需要构建其几何定位仿真模型。虽然上述研究人员已经在此领域开展了相应的学术探讨, 并且得出了有价值的研究结论, 但是大多数研究是针对太阳同步轨道线阵推扫式成像卫星特点开展的。然而, 对于静止轨道高分辨率面阵成像卫星而言, 其几何定位仿真及外检校过程如何开展, 则需要做进一步的研究, 这对优化仿真体系及掌握该卫星影像几何定位误差来源具有重要意义。
本文以GF-4卫星可见光近红外通道影像为例, 首先构建其严格成像模型, 利用C++编程语言实现了几何定位仿真。然后顾及相机姿态角常差, 利用不同区域、不同时相的GF-4卫星影像及SRTM DEM开展几何外检校, 同时分析地面控制点分布对几何外检校的影响。最后, 利用外检校参数对几何定位仿真模型进行优化, 提高影像几何定位仿真精度。
1 几何定位仿真及外检校原理 1.1 静止轨道面阵相机严格几何成像模型严格几何成像模型的构建是开展几何定位仿真的重要理论基础。一般情况下对于静止轨道面阵相机而言, 像点坐标同样需要经过多个坐标系(像面坐标系、像空间坐标系、卫星本体坐标系、轨道坐标系、J2000坐标系和WGS-84坐标系等)的转换后才能得到像点在WGS-84坐标系下的坐标。在实际应用中, 需要根据静止轨道面阵相机特点进行适当调整[11]。对于GF-4卫星而言, 其严格成像模型为[7, 10]
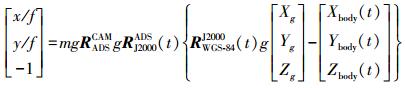 (1)
(1) 式中, (x, y)为像点P在像平面坐标系下的坐标; f为相机焦距; m为尺度系数; [Xbody(t), Ybody(t), Zbody(t)]表示投影中心在J2000坐标系下的坐标; (Xg, Yg, Zg)为该像点P对应的物方点在WGS-84坐标系下的坐标; RADSCAM、RJ2000ADS(t)和RWGS-84J2000(t)分别为姿态测量系统ADS坐标系到相机坐标系、J2000坐标系到ADS坐标系、WGS-84坐标系到J2000坐标系的旋转矩阵。
1.2 几何外检校方法相关研究结果表明影响影像定位精度的因素主要是定轨测姿精度及相机安装误差[2, 6]。对于国产卫星而言, 我国的定轨精度可以达到分米级, 其误差对影像直接定位精度的影响可以忽略, 但是我国现有的星载测姿设备的测量精度并不高, 并且通常存在常差, 这对于高轨卫星影像定位精度的影响更为明显[12]。另外, 在卫星发射过程中及发射后, 相机所处环境的变化, 导致实验室测量得到的安装角度发生改变, 使其不能够直接用于影像高精度定位[13]。由于相机安装误差与测姿误差对定位结果的影响是一致的, 因此在进行几何外检校时, 通常情况下构建一个偏移矩阵, 以提高影像直接定位精度[14]。
由于相机姿态角误差的存在, 需要利用姿态角(φ, ω, κ)构建偏移矩阵RU(φ, ω, κ), 使得式(1)左右两端相等, 则式(1)可变为
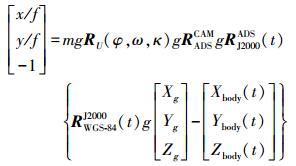 (2)
(2) 对式(2)进行泰勒公式一次展开, 可得误差方程为
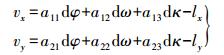 (3)
(3) 式中, (vx, vy)为坐标观测残差值; (lx, ly)为像点真实值坐标与利用地面坐标计算得到的像面近似坐标之间的差值; a11—a23的表达式分别为
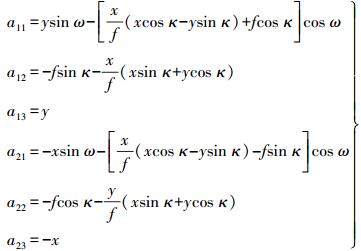 (4)
(4) 当控制点个数超过3个时, 可采用最小二乘的方法迭代计算。当姿态角改正数(dφ, dω, dκ)小于预先设定的阈值时, 停止迭代, 即可得到相机姿态角误差参数。
2 试验结果与分析 2.1 GF-4卫星影像几何定位仿真本文基于上述严格成像模型, 结合传感器设计参数及轨道仿真参数, 采用C++编程语言, 实现了GF-4卫星影像几何定位仿真, 并且利用多景不同时相的GF-4卫星在轨真实成像影像(相关成像参数见表 1)对该仿真结果精度进行检验。
| (°) | |||||
| 序号 | 成像时间 | 产品号 | 成像姿态参数 | ||
| 偏航角 | 俯仰角 | 滚动角 | |||
| 影像1 | 2016-10-05 | 146151 | -0.000 249 852 | 1.239 42 | 6.180 1 |
| 影像2 | 2016-11-11 | 148825 | -0.000 286 492 | 1.230 01 | 6.170 1 |
| 影像3 | 2016-07-23 | 123755 | -0.000 189 949 | 1.153 69 | 6.172 06 |
| 影像4 | 2017-07-24 | 169107 | -0.000 213 177 | 1.349 65 | 5.048 1 |
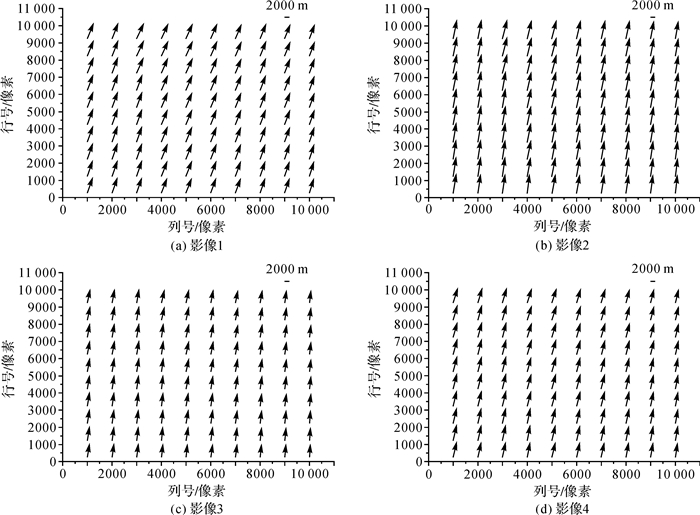
为验证构建的仿真结果几何定位精度, 本文从每景影像(10 240×10 240像素)中每隔1000个像素提取检查点坐标, 每景共计100个检查点。通过比较几何定位仿真影像与在轨真实影像中同一像点坐标可以看出, 两者存在明显的系统定位误差, 并且该仿真定位误差结果并不符合GF-4卫星光学镜头畸变规律, 如图 1和表 2所示[7]。
|
| 图 1 初始几何仿真定位误差 |
| m | ||||||||
| 序号 | 产品号 | 平均误差 | 标准差 | |||||
| X方向 | Y方向 | 平面 | X方向 | Y方向 | 平面 | |||
| 影像1 | 146151 | 68 688.005 | 26 102.322 | 73 511.259 | 1 685.614 | 2 273.738 | 1 852.967 | |
| 影像2 | 148825 | 84 485.129 | 15 361.011 | 85 904.599 | 1 787.601 | 2 472.226 | 1 829.039 | |
| 影像3 | 123755 | 60 516.498 | 10 077.207 | 61 380.298 | 1 617.718 | 2 024.997 | 1 713.301 | |
| 影像4 | 169107 | 66 707.459 | 16 615.526 | 68 782.534 | 2 132.792 | 2 227.301 | 2 093.365 | |
在对影像进行几何外检校时, 控制点的选择十分重要。但是与传统的在轨传感器几何检校有所不同, 本文主要是对所构建的几何仿真模型精度进行优化, 使其能够更为准确地反映真实在轨影像定位信息。因此, 本文所选择的控制点是从真实在轨成像影像中提取的, 而并非通过GPS或其他高精度参考影像获取控制点信息[15]。下面将重点分析仿真控制点的分布情况对GF-4卫星影像几何外检校的影响。
以影像1为例, 本文选取该区域SRTM DEM作为控制点高程信息, 在该景影像中间隔不同像素(100、200、300、400、500、600、700、800、900、1000、1500、2000、2500、3000、3500、4000、4500、5000)提取控制点信息, 利用这些控制点求取相机姿态角误差参数, 设定姿态角改正数中最大值小于10-6°时, 停止迭代。
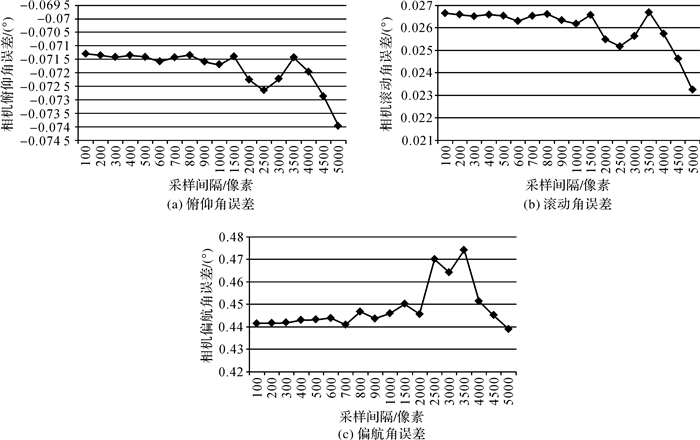
由图 2可知, 虽然迭代所设定的阈值相同, 但是仿真控制点分布的不同会导致相机姿态角误差结果有所差异, 当控制点采样间隔小于1000像素时, 计算结果差异较小。由于GF-4卫星轨道高度为36 000 km, 当相机姿态角误差为0.29″时, 对应地面的定位误差约为1像素(50 m)。因此, 本文在设置迭代阈值时, 还限定了前后迭代结果差异小于0.29″时, 获取的相机姿态角误差才为最终计算结果。
|
| 图 2 控制点分布的影响分析 |
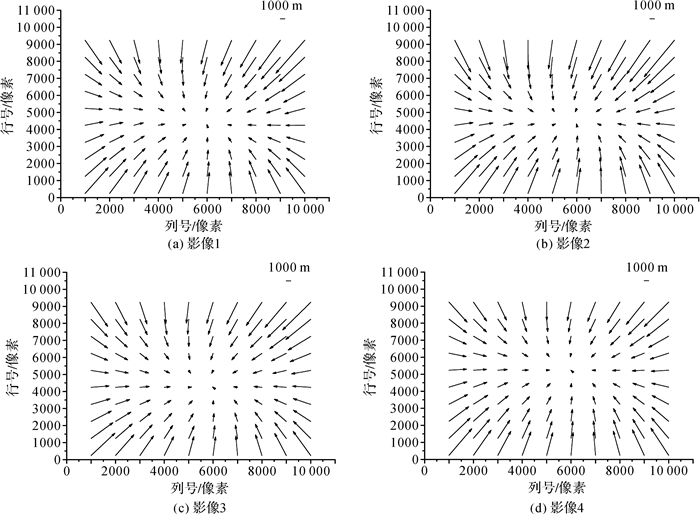
将上述外检校结果代入式(2)中, 补偿相机姿态角误差, 统计2.1中相同检查点的定位仿真结果与真实影像定位结果的差异。从图 3中可以看出, 该仿真定位误差具有高度的中心对称性, 越靠近图像边缘, 镜头畸变及感光面的缩放等所引起的对称性误差越大, 该仿真结果与文献[7]所得结论相似, 因此证明了经外检校后的定位仿真模型能够很好地模拟GF-4卫星在轨真实定位误差。
|
| 图 3 几何外检校后的定位仿真误差 |
(1) 本文针对高轨静止面阵相机特点, 以GF-4卫星相机为例, 构建了该相机的几何定位仿真模型, 形成了几何外检校方法。
(2) 本文在分析了仿真控制点分布对外检校结果的影响后, 获取了精确的相机姿态角误差参数, 并利用该结果优化了初始几何仿真模型, 使其能够有效地反映GF-4卫星在轨真实影像的几何定位误差。
(3) 由于试验数据有限, 本文只选取了部分GF-4卫星在轨真实影像进行几何仿真方法验证, 而几何外检校获得相机姿态角误差参数是否会随相机外界热环境变化出现周期性波动, 则需进一步分析。
致谢: 感谢中国资源卫星应用中心为本文研究提供GF-4卫星影像数据。| [1] | 祝小勇, 张过, 唐新明, 等. 资源一号02B卫星影像几何外检校研究及应用[J]. 地理与地理信息科学, 2009, 25(3): 16–18. |
| [2] | 袁修孝, 余翔. 高分辨率卫星遥感影像姿态角系统误差检校[J]. 测绘学报, 2012, 41(3): 385–392. |
| [3] | 李奇峻, 范大昭, 陈伟宏, 等. 资源三号卫星多光谱影像的姿态角常差检校[J]. 测绘科学, 2017, 42(2): 110–114. |
| [4] | 孟伟灿, 朱述龙, 曹闻, 等. TDI CCD交错拼接推扫相机严格几何模型构建与优化[J]. 测绘学报, 2015, 44(12): 1340–1350. |
| [5] | 杨博, 王密. 资源一号02C卫星全色相机在轨几何定标方法[J]. 遥感学报, 2013, 17(5): 1175–1190. |
| [6] | 牛常领, 童小华, 刘世杰. 资源三号卫星姿态检校方法[J]. 遥感信息, 2017, 32(1): 23–27. |
| [7] | 王密, 程宇峰, 常学立, 等. 高分四号静止轨道卫星高精度在轨几何定标[J]. 测绘学报, 2017, 46(1): 53–61. DOI:10.11947/j.AGCS.2017.20160300 |
| [8] | 皮英冬, 杨博, 李欣. 基于有理多项式模型的GF4卫星区域影像平差处理方法及精度验证[J]. 测绘学报, 2016, 45(12): 1448–1454. DOI:10.11947/j.AGCS.2016.20160262 |
| [9] | 王殿中, 何红艳. "高分四号"卫星观测能力与应用前景分析[J]. 航天返回与遥感, 2017, 38(1): 98–106. |
| [10] | 常学立. 静止轨道高分辨率面阵相机几何处理关键技术研究[D]. 武汉: 武汉大学, 2015. https://mall.cnki.net/lunwen-1016018414.html |
| [11] | 王涛, 张艳, 张永生, 等. 高分辨率遥感卫星传感器严格成像模型的建立及验证[J]. 遥感学报, 2013, 17(5): 1087–1102. |
| [12] | 周楠, 何红艳. 星载线阵遥感器在轨几何外检校技术研究[J]. 航天返回与遥感, 2016, 37(5): 111–118. |
| [13] | 曹毓, 冯莹, 赵立双, 等. 相机姿态安装误差对单目视觉定位精度的影响[J]. 传感器与微系统, 2012, 31(12): 23–26. DOI:10.3969/j.issn.1000-9787.2012.12.007 |
| [14] | 蒋永华, 张过, 唐新明, 等. 资源三号测绘卫星三线阵影像高精度几何检校[J]. 测绘学报, 2013, 42(4): 523–529. |
| [15] | 樊文锋, 李鸿洲, 温奇, 等. 高分二号卫星影像正射纠正精度分析[J]. 测绘通报, 2016(9): 63–66. |



