影像分割是遥感信息提取的重要预处理过程, 是面向对象分类[1]和目标地物提取[2]的基础。能否有效地将地物与周围地物分割开直接影响后续分类或提取的准确性。基于区域增长的分割方法是最常用的影像分割方法, 研究者们提出了多种不同的区域增长影像分割方法[3-8]。这些区域增长分割方法研究焦点在于区域增长中同质性指数和合并顺序设计[3-6], 以及在增长过程中加入区域大小约束[7-8]。其中, 分形网络演化算法[4](fractal net evolution approach, FNEA)在同质性准则中集成了光谱和形状信息, 并采用双向最优的合并准则, 具有较好的分割效果, 已内嵌入商业软件eCognition中。国内外诸多研究者也在初始分割[9~12]、合并策略控制[13-14]及并行处理[15]等方面对FNEA算法进行改进。区域增长分割方法中判断区域是否合并的相似性准则对分割结果具有至关重要的影响, 高分辨率影像地物细节信息丰富, 需要利用多种特征判断相似性。有的研究中采用分阶段区域增长过程, 在不同的阶段采用不同层次的各种特征计算相似性指数和确定合并准则[6, 16], 在复杂场景的情况下取得较好的分割结果。分水岭变换是另一种常用的遥感影像分割方法, 其特点是分割效率很高。国内外研究者针对遥感影像特点, 在梯度计算[17]、边缘约束[18]、自适应标记提取[19]、基于动态分水线的多尺度获取[20]等方面对分水岭变换分割方法进行改进。分水岭变换与区域增长方法结合使用, 为区域合并过程提供初始分割结果[9-11]。
区域增长是从种子点开始按照一定的合并准则不断合并周围相似像素或区域的过程。基于区域增长的分割算法有两个关键过程:种子点的选择(即起始区域增长点的选择)和区域增长中的对象合并准则(即两个对象满足何种相似性准则才能合并)。已有的分割方法如FNEA等都是从单个像素开始进行合并, 在像素合并的初始阶段对合并的顺序非常敏感, 需要施加额外的控制(如FNEA采用前后两次合并像素相隔尽量远的策略进行控制)。同时对于这些方法, 对象相似性是多种特征计算的相似的加权和, 权值和最终的相似性阈值通过用户设置的参数控制, 但这些参数具体含义不够明确, 往往需要通过反复的试验才能确定一组较优的参数。针对这一情况, 本文提出一种分为两步的区域增长分割算法:采用分水岭变换和简单区域合并获得一个初始分割结果, 避免种子点选择的影响; 以初始分割得到的分割区域作为基本处理单元, 利用光谱、形状和上下文信息, 基于贝叶斯准则计算两个区域的可合并概率, 进行进一步的区域合并处理。利用区域合并概率进行区域合并, 能够有效集成多种特征计算一个具有较明确含义的区域相似性指数, 同时避免了复杂的参数设置过程。
1 基于概率框架的影像分割方法 1.1 概率框架区域合并的基本思想高分辨率遥感影像上地物的几何空间信息更加明显, 特别是人工地物(如道路、房屋等)呈现明显的几何形状特征。因此, 在计算待合并区域的相似性指数时, 除光谱特征外还应该考虑纹理、边缘、形状、上下文等信息。然而这些特征往往具有不同的单位和意义, 如果通过加权相加, 则权值设置需要反复试验确定, 如FNEA算法[4]。另外, 如此计算得到的同质性因子没有直观的含义, 同样需要反复试验来确定合适的分割阈值。针对这种情况, 本文利用区域合并概率进行区域增长分割。首先对影像进行初始分割, 在初始分割对象上计算光谱统计、形状和上下文信息, 然后根据区域合并概率框架得到区域合并的概率。这既避免了不同特征间的权值设置, 而且合并概率具有一定统计含义, 便于设置合并阈值。区域合并概率框架是将两个区域是否应该合并看作一个二值变量, 分别计算区域合并和不合并的先验概率和条件概率, 根据贝叶斯准则计算二者应该合并的概率。用二值变量S表示两个相邻的区域RA、RB是否合并(SAB+表示合并, SAB-表示不合并), 对于某个特征Ck, 两个区域RA、RB的合并概率表示为
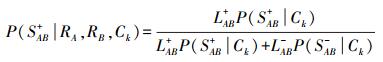 (1)
(1) 式中, LAB±=P(RA, RB|SAB±, Ck), 是指考虑特征Ck时, 两个区域是否应该合并的条件概率; P(SAB±|Ck)是使用特征Ck进行判断的先验概率。文献[22]中针对日常普通图像分割设计了先验概率和条件概率计算方法, 但并不适合遥感影像分割。本文中考虑遥感影像的特点, 综合利用光谱统计、形状和上下文信息计算相邻区域的可合并概率。其中, 条件概率密度是根据两个区域及周围上下文区域的Ck特征统计信息计算的。先验概率是根据两个区域的几何特征关系来确定的。
1.2 初始分割本文采用分水岭变换和简单的区域合并对影像进行初始分割。分水岭变换具有计算速度快、边界准确的优点, 且无需进行复杂的参数设置。常用的分水岭分割是基于标记的模拟浸水算法, 标记的选择对最终分割结果有重要影响。在提取分割标记时, 应该提取地物内部的平滑像素作为标记像素, 而尽量避免选择地物边缘处的像素。在本文中, 对于每个像素P采用以下公式通过表示像素的局部平滑性
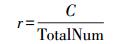 (2)
(2) 式中, C是在以像素P为圆心的圆形邻域内梯度值大于像素P梯度值的像素个数; TotalNum是整个邻域内像素个数。平滑因子r的值越大表示该像素相对于周围像素越平滑, 且与像素具体的梯度值大小无关, 可以设定一个简单的阈值提取整个影像上的标记像素进行分水岭变换分割。分水岭变换分割结果一般较为细碎, 本文通过一个简单区域合并的过程进一步合并。该过程中采用FNEA中的光谱同质性指数[4]基于双向最优准则合并。
1.3 先验概率和条件概率计算在本文的概率框架中利用相邻区域的形状符合性表示合并先验概率, 所使用的形状特征是FENA中证明非常有效的紧致性(compact)和光滑性(smooth), 具体计算公式见参考文献[4]。设区域RA有n个邻域Ri, i=1, 2, …, n, 则根据RA与某个邻域对象Rk虚拟合并前后的特征比衡量二者形状符合性, 即
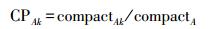 (3)
(3) 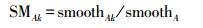 (4)
(4) 取紧致性和光滑性形状符合指标的最大值为两个区域的形状符合指标
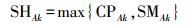 (5)
(5) 然后在RA所有邻域对象之间作归一化处理, 得到最终的合并先验概率和非合并先验概率
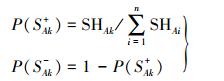 (6)
(6) 条件概率则是根据两个区域及周围上下文区域的Ck特征统计信息计算的。同一地物内部具有较高的匀质性而与相邻地物之间存在较高的差异性。利用这一特点, 对m个波段的特征Ck(k=1, 2, …, m)分别计算其合并和不合并的条件概率
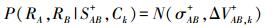 (7)
(7) 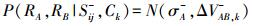 (8)
(8) 式中, N表示正态分布; ΔVAB, k+=abs(VA, k-VB, k)、ΔVAB, k-=1/abs(VA, k-VB, k), VA, k、VB, k分别是RA和RB的特征Ck均值; σAB+是RA和RB合并后的特征值标准差; σA-是A与邻接对象的特征值差倒数的面积加权均方根。然后, 就可以根据式(3)计算P(SAB+|RA, RB, Ck), 取同类特征中最小的概率值作为最终合并概率
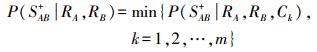 (9)
(9) 得到合并概率后, 可以利用区域合并概率进行区域合并影像分割。在分割过程中, 除判断两个区域的合并概率是否大于给定的阈值外, 还采用双向最优约束准则, 即两个区域互为对方的最大合并概率区域时才将其合并。
2 试验与分析本文试验影像是合肥市开发区的QuickBird多光谱影像, 利用影像的绿、红和红外3个波段合成为一幅彩红外影像。本文截取其中的典型区域进行试验, 如图 1(a)所示。影像上地物类型丰富, 包含自然地物(如水体、植被、裸地等)和人工地物(如房屋、道路、塑胶操场等), 其中既有尺度较大的地物(如大面积的水体和较长的公路), 也有尺度较小的地物(如居民楼和花坛等)。利用Sobel算子对影像进行计算得到影像的梯度图, 如图 1(b)所示。从图中可以看出, 在整个影像上梯度值分布不均匀, 如在水体和塑胶操场的边缘, 像素梯度值相对较低; 而在密集居民区和公路内部, 像素梯度值也相对较高。因此需要考虑区域局部信息提取平滑像素作为标记, 平滑因子阈值设为0.75, 可以得到均匀分布的标记图像, 如图 1(c)所示。利用提取的标记, 采用分水岭变换对影像进行分割, 如图 1(d)所示。从图中可以看出, 除部分道路分割区域较完整, 整个影像分割的比较细碎。进一步采用简单区域合并(阈值设为5000)得到的初始分割结果, 如图 1(e)所示。尽管初始分割得到的仍然是一个过分割的结果, 但分割区域已经具有一定的大小, 可以计算区域统计、邻域上下文和形状信息用于后续合并处理。

|
| 图 1 试验影像与分割结果 |
本文所建立的概率框架可以适合于多类特征, 在试验中使用了原始光谱特征和色度特征。色度特征是通过对原始影像进行LUV色度空间变换, 提取两个颜色分量得到的。在试验中, 先进行基于光谱特征概率的合并, 再进行基于色度特征概率的合并, 二者的概率阈值均设为0.6, 最终得到的分割结果如图 1(f)所示。从图中可以看出, 本文分割结果的区域边界准确, 无论是对于大尺度地物(如水体、植被、裸地等), 还是对于小尺度地物(如操场跑道、花坛等)均可得到完整而准确的分割结果。
将本文结果与eCognition的多尺度分割算法进行对比。eCognition分割过程中设置形状因子0.4, 光滑性和紧致性因子均为0.5, 选择3个不同的尺度参数40、80和160获得多尺度分割结果。为了获得更好的显示效果, 对分割对象采用均值加边缘的显示方法。从图 2中可以看出当尺度较小时, eCognition明显存在较多的过分割; 当尺度增大时, 过分割得到缓解, 但在水体和左侧道路处仍然存在较严重的过分割, 而同时部分小尺度地物(如花坛和游泳池)已被合并到其他地物中; 进一步增大尺度因子, 尽管在水体处仍存在过分割, 在影像其他地区已经存在较多的错误合并(欠分割)。相比之下, 本文方法对于不同尺度的地物均能得到完整准确的分割结果, 既能获得面积较大、形状完整的水体和道路分割区域, 同时也保留了花坛等小尺度地物。

|
| 图 2 本文方法与eCognition不同尺度分割结果对比 |
本文采用文献[22]中的评价指标对分割结果进行定量评价, 分别是评价分割区域内部同质性的同质性指标(HM)及评价相邻区域之间差异性的异质性指标(HT)。HM是根据分割区域的标准差的加权平均值计算的, 其值越小, 代表区域同质性越高; HT是根据相邻分割区域的灰度平均值的相关性计算的, 其值越小, 代表区域间的异质性越高。同时本文还统计了不同分割方法得到分割区域的数目(NUM)、最小面积(MINS)和最大面积(MAXS)。HM反映了分割区域内部一致性, 随着分割区域大小的增加, 其内部一致性下降。从表 1可以看出, 本文方法分割结果的区域同质性指标明显优于尺度160的分割结果, 与尺度80的分割结果相当, 证明本文方法结果具有较好的内部一致性。本文结果的同质性指标比eCognition尺度40的结果要差, 这是因为尺度较小时, 分割区域多而细碎, 区域内部的方差比较小。实际上从图 2(b)可以看出尺度40的结果存在较多的过分割。HT反映了相邻分割区域间的差异性, 区域间的差异性越大, 说明分割结果存在的过分割越少。比较本文方法与eCognition分割结果的异质性指标可知, 本文方法的HT数值明显小于eCognition不同尺度的结果, 证明本文分割的区域之间具有更大的差异性, 能够更好地分割区分不同地物。同时, 表 1中分割区域的最大、最小面积对比也说明本文分割结果具有更好的尺度无关性。总之, 本文提出的概率框架与尺度无关, 可以在同一次分割中得到不同尺度的分割区域, 分割区域的边界准确, 形状较完整, 取得的分割结果较为理想。
| 指标 | 不同尺度的eCognition分割结果 | 本文方法 | ||
| 40 | 80 | 160 | ||
| NUM | 859 | 255 | 83 | 510 |
| MINS | 14 | 191 | 144 | 12 |
| MAXS | 4879 | 9833 | 27 948 | 24 227 |
| HM | 18.5 | 25.1 | 32.8 | 25.4 |
| HT | 0.23 | 0.07 | 0.04 | -0.004 |
本文设计了一个两步法的区域增长影像分割方法。通过基于标记的分水岭变换和简单区域合并获得一个初始分割结果作为后续区域增长的基础。通过初始分割避免了种子点选择, 从而避免了区域增长的初始阶段对合并顺序敏感的问题。将初始分割区域的统计、上下文和形状信息集成到一个合并概率计算框架中, 可以得到一个不仅具有直观的概率统计意义, 而且与尺度无关的相似性度量——区域合并概率。因此, 基于区域合并概率进行区域增长影像分割, 不仅可以避免复杂的参数选择过程, 而且可以在一次分割过程中同时成功分割出不同尺度的地物。
本文提出的概率框架适用于多种不同的特征。在目前的试验中, 只应用了光谱特征和色度特征。在本文方法中, 还可以应用其他更复杂的特征(如边缘强度、纹理特征等)来计算区域相似性概率; 此外, 针对某类特殊地物的特征值(如植被指数、水体指数等), 也可以应用本文的概率框架计算包含特殊地物区域的相似性概率。这些将是下一步的主要研究方向。
| [1] | BENZ U C, HOFMANN P, WILLHAUCK G, et al. Multi-resolution, Object-oriented Fuzzy Analysis of Remote Sensing Data for GIS-ready Information[J]. ISPRS Journal of Photogrammetry & Remote Sensing, 2004, 58(3): 239–258. |
| [2] | 赵泉华, 常波, 王玉, 等. 结合模糊分割和遗传算法的航空影像车辆提取方法[J]. 测绘通报, 2017(8): 62–66. |
| [3] | WOODCOCK C, HARWARD V J. Nested-hierarchical Scene Models and Image Segmentation[J]. International Journal of Remote Sensing, 1992, 13(16): 3167–3187. DOI:10.1080/01431169208904109 |
| [4] | BAATZ M, SCHÄPE A. An Optimization Approach for High Quality Multi-scale Image Segmentation[C]//Beiträge Zum AGIT-Symposium. [S. l. ]: AGIT, 2000: 12-23. |
| [5] | NOCK R, NIELSEN F. Statistical Region Merging[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2004, 26(11): 1452–1458. |
| [6] | BYUN Y, KIM D, LEE J, et al. A Framework for the Segmentation of High-resolution Satellite Imagery Using Modified Seeded-region Growing and Region Merging[J]. International Journal of Remote Sensing, 2011, 32(16): 4589–4609. DOI:10.1080/01431161.2010.489066 |
| [7] | CASTILLA G, HAY G J, RUIZ J R. Size-constrained Region Merging (SCRM):An Automated Delineation Tool for Assisted Photointerpretation[J]. Photogrammetric Engineering & Remote Sensing, 2008, 74(4): 409–419. |
| [8] | SANZ T R, STAMON G, LOUCHET J. Using Colour, Texture, and Hierarchial Segmentation for High-resolution Remote Sensing[J]. ISPRS Journal of Photogrammetry & Remote Sensing, 2008, 63(2): 156–168. |
| [9] | CHEN Z, ZHAO Z, GONG P, et al. A New Process for the Segmentation of High Resolution Remote Sensing Imagery[J]. International Journal of Remote Sensing, 2006, 27(22): 4991–5001. DOI:10.1080/01431160600658131 |
| [10] | CHEN Zhong, WANG Guoyou, LIU Jianguo. A Modified Object-oriented Classification Algorithm and Its Application in High-resolution Remote-sensing Imagery[J]. International Journal of Remote Sensing, 2012, 33(10): 3048–3062. DOI:10.1080/01431161.2011.625055 |
| [11] | LI H, GU H, HAN Y, et al. An Efficient Multiscale SRMMHR (Statistical Region Merging and Minimum Heterogeneity Rule) Segmentation Method for High-resolution Remote Sensing Imagery[J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2009, 2(2): 67–73. |
| [12] | WANG L, GONG P, YING Q, et al. Settlement Extraction in the North China Plain Using Landsat and Beijing-1 Multispectral Data with an Improved Watershed Segmentation Algorithm[J]. International Journal of Remote Sensing, 2010, 31(6): 1411–1426. DOI:10.1080/01431160903475332 |
| [13] | YI L, ZHANG G, WU Z. A Scale-synthesis Method for High Spatial Resolution Remote Sensing Image Segmentation[J]. IEEE Transactions on Geoscience & Remote Sensing, 2012, 50(10): 4062–4070. |
| [14] | ZHONG Y, ZHAO B, ZHANG L. Multiagent Object-based Classifier for High Spatial Resolution Imagery[J]. IEEE Transactions on Geoscience & Remote Sensing, 2013, 52(2): 841–857. |
| [15] | HU Z, LI Q, ZOU Q, et al. A Bilevel Scale-sets Model for Hierarchical Representation of Large Remote Sensing Images[J]. IEEE Transactions on Geoscience & Remote Sensing, 2016, 54(12): 7366–7377. |
| [16] | 刘婧, 李培军. 结合结构和光谱特征的高分辨率影像分割方法[J]. 测绘学报, 2014, 43(5): 466–473. |
| [17] | 肖鹏峰, 冯学智, 赵书河, 等. 基于相位一致的高分辨率遥感图像分割方法[J]. 测绘学报, 2007, 36(2): 146–151. |
| [18] | LI D, ZHANG G, WU Z, et al. An Edge Embedded Marker-based Watershed Algorithm for High Spatial Resolution Remote Sensing Image Segmentation[J]. IEEE Transactions on Image Processing, 2010, 19(10): 2781–2787. DOI:10.1109/TIP.2010.2049528 |
| [19] | 巫兆聪, 胡忠文, 欧阳群东. 一种区域自适应的遥感影像分水岭分割算法[J]. 武汉大学学报(信息科学版), 2011, 36(3): 293–296. |
| [20] | LI P, GUO J, SONG B, et al. A Multilevel Hierarchical Image Segmentation Method for Urban Impervious Surface Mapping Using Very High Resolution Imagery[J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2011, 4(1): 103–116. |
| [21] | ALPERT S, GALUN M, BASRI R, et al. Image Segmentation by Probabilistic Bottom-up Aggregation and Cue Integration[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(2): 315–327. DOI:10.1109/TPAMI.2011.130 |
| [22] | MING D, CI T, CAI H, et al. Semivariogram-based Spatial Bandwidth Selection for Remote Sensing Image Segmentation with Mean-shift Algorithm[J]. IEEE Geoscience & Remote Sensing Letters, 2012, 9(5): 813–817. |


