精密单点定位技术(precise point positioning, PPP)即利用载波相位观测值及由IGS等组织提供的高精度的卫星星历与卫星钟差, 应用单台接收机进行静态或动态独立定位, 能够直接获得静态厘米级、动态分米到厘米级的高精度的坐标结果, 它在形变监测、实时GNSS气象学、高精度导航定位与精密授时等领域得到了广泛的应用[1-2]。随着实时精密定轨和实时精密钟差估计等理论与算法的发展, PPP技术已成为一种获得实时高精度坐标的重要手段。许多机构和科研人员在此方面作了深入的研究。Gao和Chen使用JPL提供的实时轨道和钟差改正数据进行了实时PPP试验, 并对定位结果进行了分析[3]。江楠等利用IGU预报轨道进行实时钟差估计, 从而获得了实时PPP定位结果, 试验表明实时PPP定位精度可以达到厘米级, 但是其收敛时间较长, 约20 min[4]。Altiner应用BKG提供的实时改正数产品对CONZ站进行17 h的实时PPP计算, 结果得出, CONZ的水平方向和高程方向的精度分别约为10和20 cm[5]。IGS (The International GNSS Service)于2007年首次提出IGS实时项目(real time pilot project, RTPP), 基于全球范围内的实时观测数据, 为用户提供实时的轨道和钟差产品, 通过6年的试验与测试, 于2013年4月实现了全球范围内的实时服务(RTS), 可为用户提供全球范围内的GPS轨道钟差改正数产品, 实时钟差的精度优于0.3 ns, 同时对GLONASS的改正产品进行全球范围的测试[6]。上述研究成果为实时PPP解算提供了相关的数据与理论基础, 但较长的收敛时间制约了实时PPP的实际应用。
在GNSS定位过程中, 对流层延迟是影响其定位精度与收敛速度的重要因素。研究表明, 卫星信号受对流层延迟影响造成天顶方向误差可达2 m[7]。因此, 有学者研究应用实时区域对流层模型来缩短实时PPP的收敛时间, 并取得相关成果。Shi等通过最优拟合模型获得局部对流层拟合系数, 建立实时区域对流层拟合模型。试验表明, 模型在初始化20 min后获得的水平和垂直精度分别约为9.2和10.1 cm, 比对流层延迟估计在水平和垂直精度分别提高5和10 cm[8]。Hadas利用IGS-RTS提供的实时产品, 对UNB3模型和近实时区域对流层插值模型的收敛时间和坐标精度进行了分析, 评估近实时区域对流层模型在PPP解算上的影响[9]。张小红等通过对基准站对流层建模, 利用空间回归模型内插流动站, 分析了对流层的内插精度, 但是未进行深入分析对流层内插模型对PPP定位精度和收敛时间的影响[10]。钱闯等通过分析常用的实时区域对流层模型, 提出球冠谐的区域精密对流层模型, 虽然可以提高预报精度, 但模型较为复杂, 计算量大[11]。此外, 考虑对流层延迟模型的建立与区域地形气候具有较强的相关性, 鲜有文献对中国区域对流层实时模型精度及其性能进行分析。基于此, 本文利用中国广东地区的43个CORS站的GPS观测数据, 采用非差PPP方式解算各CORS站的天顶对流层延迟, 并运用反距离加权内插法建立区域天顶对流层延迟模型, 评估模型的天顶对流层延迟改正精度, 以及对PPP定位精度和收敛时间的影响, 提高实时PPP的定位性能。
1 PPP估计天顶对流层延迟在非差数据处理过程中, 分别应用精密星历和精密钟差固定卫星轨道和消除卫星钟差项, 并且采用双频观测值消去电离层延迟的影响[12], 观测方程为
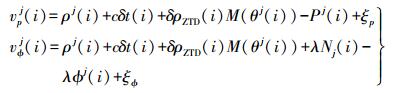 (1)
(1) 式中, j为卫星号; i为相应的观测历元; c为真空中的光速; δρZTD(i)、M(θj(i))分别为天顶对流层延迟和相应的投影函数; θj(i)为j卫星的高度角; ξp、ξφ分别为多路径、观测噪声等未模型化的误差; Pj(i)、φj(i)为相应卫星i历元消除了电离层影响的组合观测值; λ为相应的波长; ρj(i)为信号发射时刻卫星位置与信号接收时刻接收机位置之间的几何距离; Nj(i)为无电离层延迟组合的模糊度参数。
2 ZTD反距离加权内插模型反距离加权插值法是一种加权平均的插值方法, 距离待插值测站越近的CORS基准站所占的权重越大, 反之所占的权重越小[13], 能有效减小因距离增加导致对流层相关性减小而引入的模型误差。定权的基本公式为
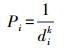 (2)
(2) 式中, 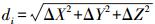
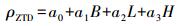 (3)
(3) 式中, B为大地纬度; L为大地经度; H为大地高。内插时, 以流动站为中心, 建立局部坐标系, B、L、H均为局部坐标系下的值。
对地面上n个CORS基准站解算的天顶对流层延迟数据建立模型
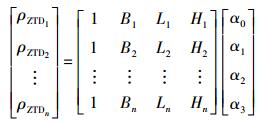 (4)
(4) 对应的向量形式为
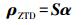 (5)
(5) 对式(5)进行加权最小二乘估计可以得到区域插值模型的系数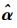
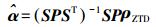 (6)
(6) 则流动站处的ρZTD可由模型的系数和该处的大地坐标根据式(7)得到
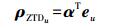 (7)
(7) 式中, eu=[1 Bu Lu Hu]T。由于Pi是由基准站与流动站之间的距离决定的, 因此对于每一个流动站都会有一组不同的模型系数α。一般认为区域范围内的对流层延迟具有连续平缓、空间相关的特征, 故利用本文提出的反距离加权法进行对流层建模内插能够很好地体现对流层的空间特性。
3 区域实测对流层延迟建模试验 3.1 试验处理与分析选取2015年11月21日(年积日DOY 325)至2015年11月23日(年积日DOY 327)的中国广东区域CORS站观测数据。
同时, 应用德国地学中心GFZ提供的卫星轨道和钟差产品, 数据采样间隔为30 s, 卫星截止高度角为10°, 采用事后静态模拟实时动态PPP解算。首先, 对基准站天顶方向的对流层延迟进行估计; 然后, 采用反距离加权方法对基准站的ZTD进行区域建模; 最后, 通过模型内插获得流动站的ZTD, 并应用于PPP解算。此外, 为了评估模型内插算法的有效性, 流动站也采用对流层参数估计方法进行解算。将参数估计得到的ZTD与模型内插值进行比较, 分析模型内插的对流层对PPP收敛时间和收敛后定位精度的影响。本文数据处理程序参数配置见表 1。
| 气温与气压模型 | GPT2 |
| 对流层干延迟ZHD | Saastamoinen |
| 对流层投影函数 | GMF |
| 对流层湿延迟ZWD | 参数估计 |
| 卫星截止高度角 | 10° |
| 采样间隔 | 30 s |
| 滤波方式 | SRIF |
精度评估时, 以Pnada软件计算的静态PPP坐标结果的均值与对流层延迟为参考值, 将实时动态PPP计算坐标结果与参考值作差, 获得E、N、U 3个方向上坐标的RMS, 以分析模型对PPP定位精度的影响; 同时, 将对流层延迟计算结果与参考值作差, 获得对流层延迟的STD来评价区域模型的精度。
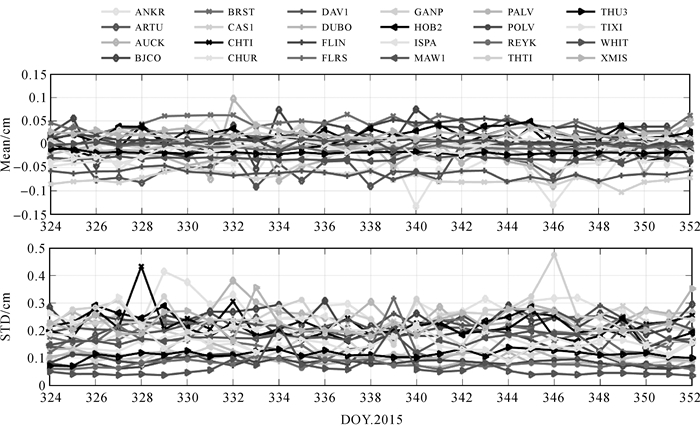
图 1给出Panda软件解算的部分IGS测站的ZTD与IGS对流层产品的差异。由图中可知, 静态PPP处理模式解算的各个测站ZTD精度均优于0.5 cm, 软件以静态PPP处理模式得到的对流层结果可以达到很好的精度。同时, 统计了Panda软件在静态PPP处理模式下得到的部分IGS测站坐标与IGS基准站的差异, 统计结果表明坐标解算结果在N、E、U 3个方向的最大值均小于5 cm, 最小值约为0.001 cm, 具有较高的精度。综上所述, Panda软件静态PPP处理结果可以作为参考值, 用以评价本文所用的区域对流层模型对PPP收敛时间和定位精度以及对流层精度的影响。
|
| 图 1 Panda静态解算的部分IGS测站的ZTD与IGS对流层产品的差异 |
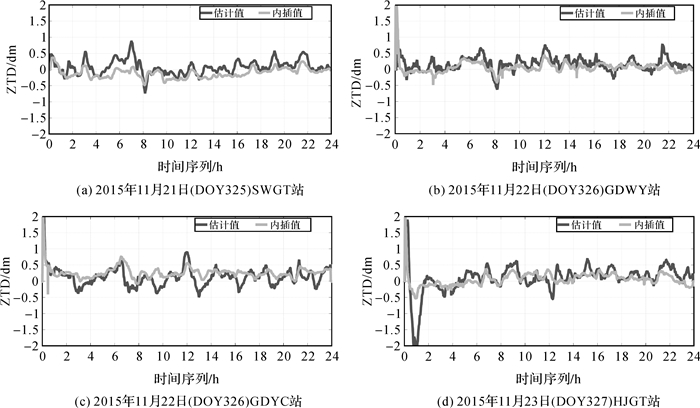
由于对流层干分量比较稳定, 可以通过对流层改正模型准确获得, 因此, 在估计对流层天顶方向的湿延迟前, 利用Saastamoinen模型对其干延迟进行模型改正, 干湿分量均采用GMF投影函数。首先, 由流动站与基准站间的距离利用式(2)得到模型的权P; 然后, 将基准站天顶方向的对流层总延迟代入式(6)中得到模型系数α; 最后, 由式(7)获得流动站的天顶对流层的总延迟。图 2给出了区域天顶对流层延迟模型值和ZTD参数估计值与对流层参考值间的差异。可以看出, 收敛后ZTD模型值与参考值的差值均在-0.5~0.5 cm范围内, 其精度优于ZTD估计值的精度。
|
| 图 2 ZTD参数估计值和模型改正值与对流层参考值的差异 |
表 2统计了天顶方向对流层延迟的估计值和模型值与参考值之间差值的STD。结果表明, 区域ZTD模型获得的天顶对流层延迟精度优于ZTD参数估计, 其精度提高约为1 cm。且测站MZGT的提高尤为明显, 3天平均STD提高约为4 cm。
| cm | |||||||
| 测站 | 对流层采用参数估计 | 对流层采用模型计算 | |||||
| DOY325 | DOY326 | DOY327 | DOY325 | DOY326 | DOY327 | ||
| GDWY | 2.65 | 2.58 | 3.15 | 1.60 | 1.34 | 1.21 | |
| GDYC | 3.20 | 2.83 | 3.66 | 3.46 | 3.09 | 4.02 | |
| HJGT | 3.50 | 3.17 | 3.48 | 1.74 | 1.77 | 2.22 | |
| MZGT | 3.19 | 3.11 | 14.67 | 3.03 | 2.92 | 2.27 | |
| SWGT | 2.35 | 3.14 | 2.39 | 1.86 | 1.32 | 1.37 | |
在实时解算中, 基准站对流层延迟估计需要一定的收敛时间, 得到较为准确的ZTD后才能用于建模。为了避免建模误差对流动站的影响, 将前3 h的数据剔除。同时, 为了对比分析对流层延迟估计和模型改正对PPP收敛时间的影响, 本文设定水平方向的收敛阈值为:N方向和E方向坐标误差小于0.1 m。高程方向的收敛阈值为:U方向坐标误差小于0.2 m, 且在接下来的20个连续观测历元的水平方向和高程方向误差均不大于0.1和0.2 m。表 3分析ZTD参数估计和模型改正对PPP收敛速度的影响。统计结果表明采用加权反距离内插模型改正, 明显缩短了PPP收敛时间, 收敛速度较ZTD参数估计提高约为70%。
| 测站 | 对流层参数估计收敛历元数 | 对流层模型改正收敛历元数 | |||||
| DOY325 | DOY326 | DOY327 | DOY325 | DOY326 | DOY327 | ||
| GDWY | 296 | 52 | 40 | 100 | 74 | 45 | |
| GDYC | 45 | 88 | 19 | 35 | 70 | 19 | |
| HJGT | 198 | 76 | 148 | 89 | 96 | 140 | |
| MZGT | 87 | 133 | 47 | 58 | 130 | 43 | |
| SWGT | 77 | 64 | 54 | 37 | 36 | 60 | |
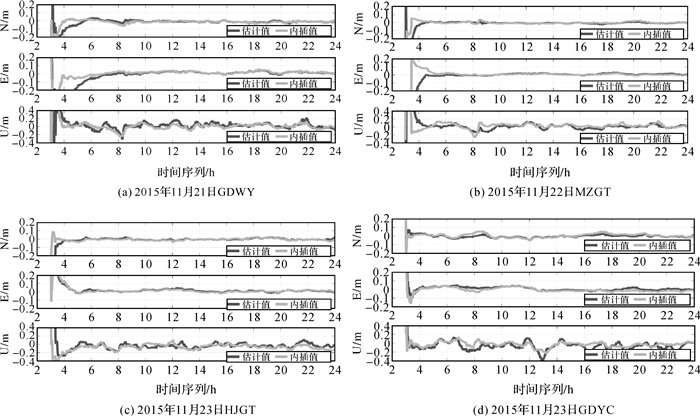
本文将Pnada软件计算的静态PPP坐标结果的均值作为参考值。将实时动态PPP计算坐标结果与参考值作差, 并将差值转换至N、E、U方向进行比较。分别统计对流层延迟估计和模型改正在E、N、U 3个方向的RMS, 以分析两种对流层延迟处理模式对PPP定位精度的影响。统计结果表明, 对流层延迟估计和模型改正在E和N方向的定位精度相当, 约为2 cm; 在U方向, 模型改正的定位精度近似于5 cm, 对流层延迟估计大约为10 cm, 因此模型改正在该方向的定位精度明显优于对流层延迟估计。如图 3所示。
|
| 图 3 ZTD估计和模型改正对PPP定位的影响 |
本文应用反距离加权内插法, 对试验区域内解算基准站的ZTD结果建立实时区域天顶对流层延迟模型, 评估该模型对PPP收敛时间和定位精度的影响。试验表明: PPP解算在水平E和N方向上, 实时区域对流层延迟模型获得的定位精度与天顶对流层参数估计相当, 均为2 cm; 但在高程U方向, 模型改正的效果明显优于对流层参数估计, 其精度提高大约5 cm; 同时, ZTD模型改正比天顶对流层延迟参数估计需要更短的收敛时间, 其收敛速度较ZTD参数估计提高约为70%。
| [1] | ZUMBERGE J F, HEFLIN M B, JEFFERSON D C, et al. Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks[J]. Journal of Geophysical Research(Solid Earth), 1997, 102(B3): 5005–5017. |
| [2] | 李征航, 黄劲松. GPS测量与数据处理[M]. 武汉: 武汉大学出版社, 2010: 162. |
| [3] | GAO Y, CHEN K. Performance Analysis of Precise Point Positioning Using Real-time Orbit and Clock Products[J]. Positioning, 2004, 3(1-2): 95–100. |
| [4] | 江楠, 徐天河, 许艳. 基于IGS区域网的卫星钟差实时估计及PPP精度分析[J]. 大地测量与地球动力学, 2013, 33(5): 44–48. |
| [5] | ALTINER Y, MERVART L, SOEHNE W, et al. Real-time PPP Results from Global Orbit and Clock Corrections[J]. Egu General Assembly, 2010(12): 11969. |
| [6] | CAISSY M, AGROTIS L, WEBER G, et al. The International GNSS Real-time Service[J]. GPS World, 2012, 23(6): 52. |
| [7] | 殷海涛, 黄丁发, 熊永良. GPS信号对流层延迟改正新模型研究[J]. 武汉大学学报(信息科学版), 2007, 32(5): 454–457. |
| [8] | SHI Junbo, XU Chaoqian, GUO Jiming, et al. Local Troposphere Augmentation for Real-time Precise Point Positioning[J]. Earth, Planets and Space, 2014. DOI:10.1186/1880-5981-66-30 |
| [9] | HADAS T, KAPLON J, BOSY J, et al. Near-real-time Regional Troposphere Models for the GNSS Precise Point Positioning Technique[J]. Measurement Science and Technology, 2013, 24(5): 055003. DOI:10.1088/0957-0233/24/5/055003 |
| [10] | 张小红, 朱峰, 李盼, 等. 区域CORS网络增强PPP天顶对流层延迟内插建模[J]. 武汉大学信息学报(信息科学版), 2013, 338(6): 679–683. |
| [11] | 钱闯, 何畅勇, 刘晖. 基于球冠谐分析的区域精密对流层建模[J]. 测绘学报, 2014, 43(3): 248–256. |
| [12] | 叶世榕, 张双成, 刘经南. 精密单点定位方法估计对流层延迟精度分析[J]. 武汉大学学报(信息科学版), 2008, 33(8): 788–791. |
| [13] | 戴吾蛟, 陈招华, 匡翠林, 等. 区域精密对流层延迟建模[J]. 武汉大学学报(信息科学版), 2012, 36(4): 392–396. |


