2. 中南大学地球科学与信息物理学院, 湖南 长沙 410083
2. School of Geosciences and Info-physics, Central South University, Changsha 410083, China
Voronoi雏形可见于笛卡尔的《哲学原理》,文中描述了在可视宇宙中太阳系是由许多漩涡(Vortices)组成的这一理念[1]。在涡旋空间被抽取为凸域集合概念之后,这一概念在不同学科中被赋予了种种名称:生物学的中轴变换(medial axis transform);化学、物理学的维格那-塞茨原胞(Wigner-Seitz zones);晶体学的作用域(domains of action);气象学、几何学的泰森多边形(Thiessen polygons)等。最后,由数学家Dirichlet和Voronoi将这一概念正式命名为狄利克雷镶嵌(Dirichlet tessellation)或沃洛诺伊图(Voronoi diagram)[2]。作为计算几何的重要内容,Voronoi图是解决骨架线提取、凸包计算、Delaunay三角化,以及数据可视化等问题的有力工具[3]。因此,研究Voronoi图的高效生成算法具有重要的现实意义。
在一般Voronoi图与广义Voronoi图的生成方法上已有诸多学者进行了相关研究,主要分为矢量生成方式和栅格生成方式两种。基于矢量的Voronoi图生成方法主要有增量法、分治法、间接法,由于矢量数据的存储量大、存储结构比较复杂,对点线面复合目标构成的空间实体进行Voronoi计算时,多要求生长元是点或半线,对线或面要素则往往分解为点要素来构建Voronoi图,该方式破坏了图形的完整性,并增加了计算的复杂度[4-6]。由于矢量方法的局限性,基于栅格的Voronoi图生成方法得到研究与发展。栅格Voronoi图的生成方式一是依据传统距离变换的栅格Voronoi生成[7-10],在基于空间生长目标图像转变为距离图像的栅格Voronoi图生成方法中定义栅格距离是关键,已有的主要距离形式有欧氏距离、曼哈顿距离(或L1距离)、切比雪夫距离(或L∞距离)及其加权形式;二是基于形态学的膨胀算子生成栅格Voronoi图[11]。在提高栅格Voronoi图生成的效率方面,栅格Voronoi生成要计算每个栅格与各个发生元间的距离,因此当发生元所占栅格数量很多时,往往存在较高的时间计算复杂度。对此,文献[12]利用四叉树和区间算术,规避对背景栅格的逐项处理以提高栅格计算速度;文献[13]通过查找邻近栅格,计算背景栅格与过滤后的生长元之间的距离来判断栅格归属提高Voronoi生成效率,以及依赖处理器物理性能的Voronoi并行计算方法[14]。
虽然基于栅格的Voronoi生成方法能够处理复杂的空间实体,对生长元的约束宽松,但算法效率和计算精度是一直以来所研究的问题。通常,基于栅格生成的Voronoi图精度低、计算量大、耗时长,主要归因于在距离图上需要进行多次计算、比较每一个点与每一个生长元的距离来确定归属,已有提高栅格Voronoi图生成效率的方法主要采用邻近方式过滤出与背景栅格邻近的发生元栅格,从而减少计算次数、优化栅格Voronoi图生成效率,栅格处理过程中各个栅格的计算并不依赖于其他栅格,即是相互独立的。因此,从规避背景栅格与生长元栅格的距离计算方面,本文提出了基于地图代数的加权Voronoi图,即雷利Voronoi图(Reilly Voronoi diagram,RVD)生成方法。该方法利用雷利法则的综合权重生成每个栅格生长元的距离图,对由每个生长元生成的距离图进行地图代数计算,最后实现空间场的栅格加权Voronoi图剖分。
1 Voronoi图定义 1.1 一般Voronoi图一般Voronoi图,又称普通Voronoi图,或常规Voronoi图,或1-site Voronoi图。以空间R2点要素为例,若存在空间点状生长元集合P={p1,p2,…,pn}(n∈N*),对空间任一点q,若满足如下关系
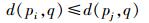 (1)
(1) 式中,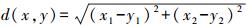
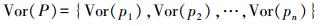 (2)
(2)

|
| 图 1 一般Voronoi图 |
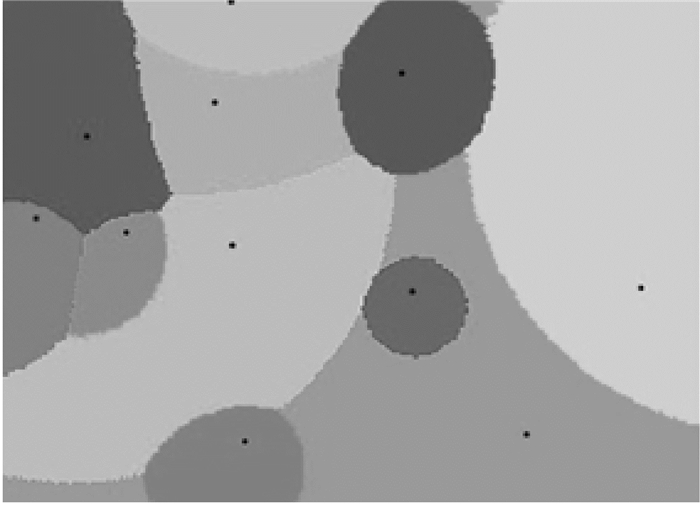
当生长元被赋予一定权重时,生成的一般Voronoi图扩展为广义Voronoi图。以空间R2点要素为例,若存在空间生长元集合P={p1,p2,…,pn},相应的权重W={w1,w2,…,wn}(n∈N*),对空间任一点q,若满足如下关系
 (3)
(3) 则称由满足条件的空间点要素所构成的区域为生长元pi的广义Voronoi图。生长元的权重越大,其广义Voronoi图就越大,所有生长元P则将该空间剖分为各自的加权Voronoi势力范围Vor(·),示意图如图 2所示。
|
| 图 2 加权Voronoi图 |
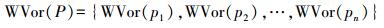 (4)
(4) 根据生长元个数及生成的空间上下文不同,广义Voronoi图又衍生出集群性生长元作用下的k阶Voronoi图[15]、受道路网影响的变速城市Voronoi图[16],网络Voronoi图[17-18]、根据方向比例计算生成的维度比率Voronoi图[19]、依据角度计算生成的角度Voronoi图[20]等形式。
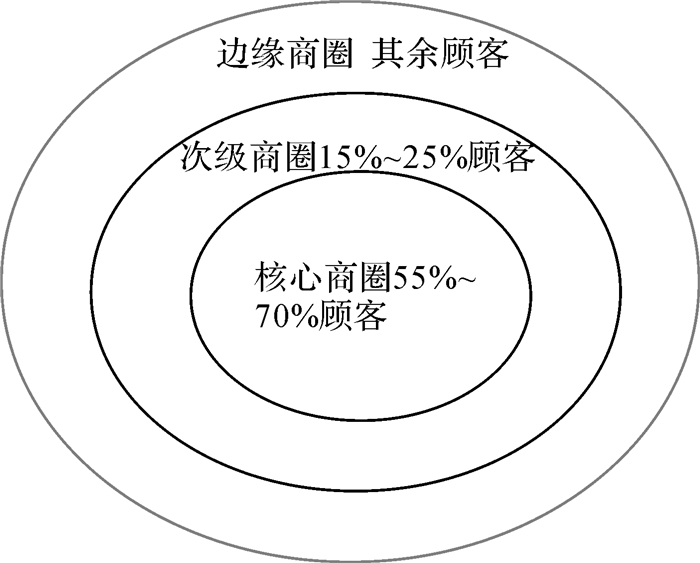
2 Voronoi地图代数计算 2.1 雷利距离变换雷利零售引力法则(Reilly’s law of retail gravitation)是由美国学者威廉·J·雷利根据牛顿力学的万有引力理论,利用3年时间调查了美国150个城市对周围地区的吸引力,总结了都市人口与零售引力的相互关系,提出了“零售引力规律”,被称为雷利法则或雷利零售引力法则。该法则描述了一个城市的吸引力与它的规模成正比,与它们之间的距离成反比,用以解释城市规模与建立的商品零售区之间的关系[21],如图 3、图 4所示的不同商圈及不同的城区规模对顾客数量、空间引力范围的描绘。
|
| 图 3 不同商圈的顾客引力 |

|
| 图 4 城区规模引力 |
城区规模不同产生的空间引力范围不同,这正是传统栅格加权Voronoi图的权重局限性,即在计算上往往注重生长元的权重大小,即规模权重,而忽略了随距离而产生的距离变换权重的影响。因此,依据雷利法则研究将Voronoi图的距离约束重新界定为
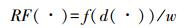 (5)
(5) 式中,f(·)函数指值域随着距离变量的增大而增大,空间目标距离生长源的距离呈现出欧氏距离变换的渐变规则,如f(d)=d+1、f(d)=d2等。尽管Voronoi图的边界复杂,难以计算,但是基于栅格Voronoi图的计算则相对易于实现。
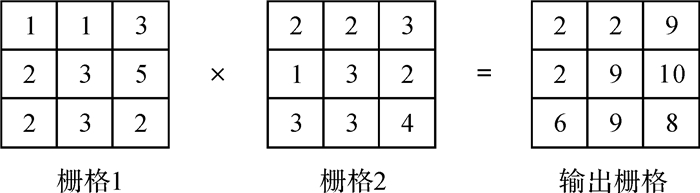
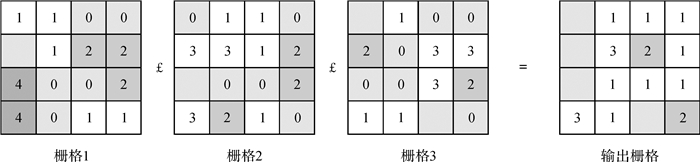
2.2 地图代数计算将连续空间离散化的栅格数据是场模型在信息系统中的具体实现。栅格的“位”数据蕴含了丰富的关系数据,更加适用于网络分析,在“数字地球”等大型地理信息工程建设的空间分析中,栅格数据展现了明显的优势[22]。地图代数研究的正是度量空间下的抽象点状要素目标集,即相应空间位置上栅格值的代数计算。与代数运算所不同的是,代数运算只有矩阵的加法和减法,是相应位置上的计算。即地图代数遵循了位置一一对应的转换规则,是空间计算的重要工具,如图 5、图 6所示的两个图幅的地图代数乘法计算。以图 5的栅格1与栅格2的第一行为例,1×2=2,1×2=2,3×3=9,得到输出栅格结果。多图幅的最低位置计算输出结果为具有最小值的像素的位置,即第几个栅格,如图 6的栅格1、栅格2与栅格3的第一行为例,像素值1£0 £ Null=Null,1 £1 £1=1(栅格1), 0 £1 £0=1(栅格1),0 £1 £0=1(栅格1),0 £0 £0=1(栅格1)。
|
| 图 5 地图代数乘法运算 |
|
| 图 6 最低位置算子£ |
结合雷利法则,本文利用地图代数的算术计算、关系计算,设计的地图代数生成栅格加权Voronoi图(RVD)的方法描述如下,生产的流程如图 7所示。

|
| 图 7 地图代数的雷利Voronoi图生成过程 |
雷利Voronoi图的地图代数生成方法为:
输入:空间点要素集合PW。
输出:PW的栅格加权Voronoi图。
(1) 对每一个空间点要素pwi∈PW,地图代数算术计算各自的欧氏栅格距离图[RDi]←[d(pwi)]。
(2) 依据雷利距离变换RT(·),地图代数算术重计算栅格距离,生成新的栅格距离变换图[NRDi]←RT(RDi)。
(3) 地图代数关系计算所有栅格距离图[NRDi]中的局部最小值←min([NRDi])。
(4) 地图代数关系计算比较minval和[NRDi],如果minval≥[NRDi],则将栅格R归属为第一个小于minval的生长元p,Rp←£(minval,[NRDi])。
(5) 算法结束。
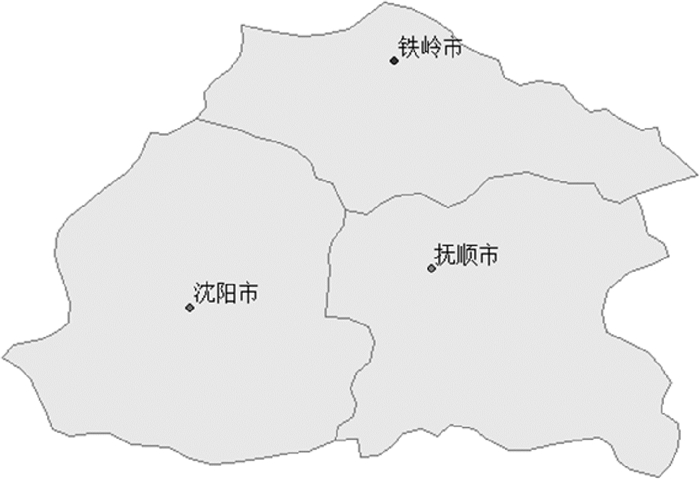
3 算例与分析研究的试验算例以辽宁省的沈阳市、抚顺市和铁岭市3个市区为研究案例,研究区示意图如图 8所示,研究提出的地图代数雷利Voronoi图生成方法利用Python 2.5.1 +ArcScripting开发实现。在雷利Voronoi图的权重界定上,本试验采用f(d)=d2的欧氏距离重计算变换方式;规模权重设置根据全国第六次人口普查获取的各市区人口统计数据作为其影响的重要性指标。从全国第六次人口普查(http://www.stats.gov.cn/ztjc/zdtjgz/zgrkpc/dlcrkpc/)公布的数据中得出沈阳8 106 171人,抚顺2 138 090人,铁岭2 717 732人,以此作为生长元的规模权重。
|
| 图 8 试验区域 |
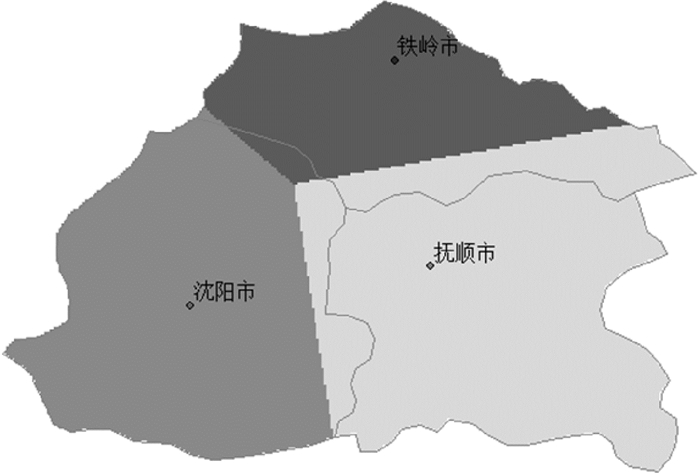
为了规避在单幅图中背景栅格与每一生长元的距离计算,试验首先对每一生长元生成其欧氏距离变换图,如图 11所示的抚顺市、沈阳市、铁岭市的欧氏栅格距离变换图。在此距离变换基础上,利用最低位置算子£实现其一般Voronoi图,如图 9所示。从各市区的一般Voronoi图可看出,各市区的作用范围与其行政区划面积大体近似,而沈阳作为省会城市其影响范围应大于周边市区,从商圈与零售引力上,普通Voronoi与市区的实际影响力不符。
|
| 图 9 市区的一般Voronoi |

|
| 图 11 各市区的欧氏距离 |
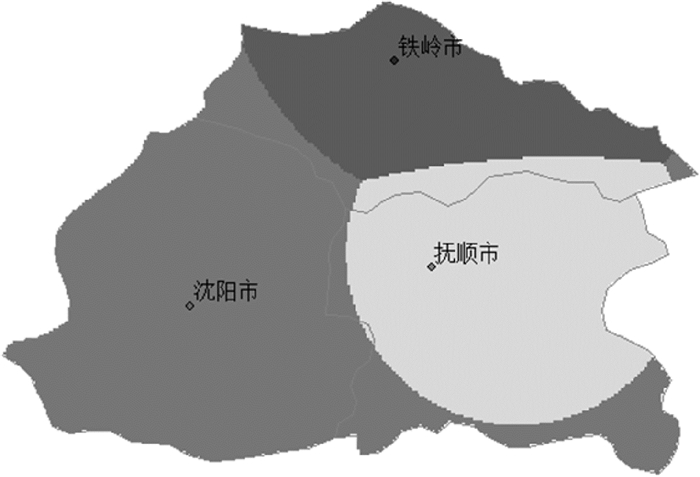
在规模权重与距离变化权重的作用下,经对各市区的欧氏距离图变换与最低位置算子£计算(如图 12所示),实现了各市区的雷利Voronoi图(如图 10 所示)。对比图 9,从图 10中可以看出作为省会的沈阳市受综合权重的影响具有更大的Voronoi作用域,远超出了其行政区划的作用范围,更符合省会城市的实际效应。此外,以此方式生成的雷利Voronoi图并未涉及背景栅格与每一个生长元的距离计算,通过简单的地图代数计算降低了计算的复杂性,规避了单幅图中由多次计算、归属判断所带来的时间复杂度。
|
| 图 10 市区的雷利Voronoi图 |

|
| 图 12 各市区的雷利变换距离 |
针对传统栅格Voronoi图生成方式中仅顾及生长元的权重局限性、单图幅中计算、判断背景栅格与每一生长元的栅格距离计算复杂性,研究基于雷利法则,从生长元的规模权重和距离变换权重出发,依据每个生长元独立生成的栅格欧氏距离图,利用地图代数的方法重计算每个生长元的权重距离图,最后,在最低位置算子作用下,对所有生长元新产生的权重距离图剖分各自的竞争空间,即雷利Voronoi图。试验证明,该方法产生的雷利Voronoi图比一般Voronoi图更符合市区对空间的影响范围,体现出了省会市区在竞争域上明显大于其行政区划范围。该方法不仅完善了权重影响因素,而且结合每个生长元的独立栅格距离图,从多个距离图幅角度,以地图代数的形式规避了在单一图幅中遍历栅格,逐一处理背景栅格所属的生长元而造成的计算效率问题;从栅格数据的精度角度,如何根据实际需求设定栅格的大小以满足Voronoi在实际中的应用是下一步工作需要继续探讨和解决的问题。
| [1] | DESCARTES R, MILLER V R, MILLER R P.Principles of Philosophy[M].Boston:[s.n.], 1908. |
| [2] | VORONOI G. Nouvelles Applications des Paramètres Continusàla Théorie des Formes Quadratiques[J]. Journal für die Reine und Angewandte Mathematik, 1908(134): 198–287. |
| [3] | 刘金义, 刘爽. Voronoi图应用综述[J]. 图学学报, 2004, 25(2): 125–132. |
| [4] | 康顺, 相诗尧. 基于马氏距离的多高斯Voronoi图生成方法[J]. 地理与地理信息科学, 2016, 32(3): 49–52. |
| [5] | 李佳田, 杨琪莉, 罗富丽, 等. 线/面Voronoi图的分解合并生成算法[J]. 武汉大学学报(信息科学版), 2015, 40(11): 1545–1550. |
| [6] | 王新生, 刘纪远, 庄大方, 等. 基于GIS的任意发生元Voronoi图逼近方法[J]. 地理科学进展, 2004, 23(4): 97–102. DOI:10.11820/dlkxjz.2004.04.012 |
| [7] | 刘宝举, 刘慧敏, 邓敏, 等. 一种基于栅格的加权Voronoi图构建普适方法[J]. 地理与地理信息科学, 2016, 32(4): 17–22. |
| [8] | DONG P. Generating and Updating Multiplicatively Weighted Voronoi Diagrams for Point, Line and Polygon Features in GIS[J]. Computers & Geosciences, 2008, 34(4): 411–421. |
| [9] | BAREQUET G, DICKERSON M T, SCOT R L. 2-Point Site Voronoi Diagrams[J]. Discrete Applied Mathematics, 2002, 122(1): 37–54. |
| [10] | LI C, CHEN J, LI Z. A Raster-based Method for Computing Voronoi Diagrams of Spatial Objects Using Dynamic Distance Transformation[J]. International Journal of Geographical Information Science, 1999, 13(3): 209–225. DOI:10.1080/136588199241328 |
| [11] | 李佳田, 陈军, 赵仁亮, 等. 基于线性四叉树结构的Voronoi图反向膨胀生成方法[J]. 测绘学报, 2008, 37(2): 236–242. |
| [12] | 寿华好, 袁子薇, 缪永伟, 等. 一种平面点集Voronoi图的细分算法[J]. 图学学报, 2013, 34(2): 1–6. |
| [13] | 王新生, 刘纪远, 庄大方, 等. 一种新的构建Voronoi图的栅格方法[J]. 中国矿业大学学报, 2003, 32(3): 293–296. |
| [14] | 王结臣, 蒲英霞, 崔璨, 等. 一种基于点集自适应分组构建Voronoi图的并行算法[J]. 图学学报, 2012, 33(6): 7–13. |
| [15] | LEE I, PERSHOUSE R, LEE K. Geospatial Cluster Tessellation Through the Complete Order-k Voronoi Diagrams[C]//International Conference on Spatial Information Theory. [S. l. ]: Springer-Verlag, 2007: 321-336. |
| [16] | 兰连意, 张有会, 杨玉平. 一般城市Voronoi图的结晶生成[J]. 计算机工程与应用, 2010(10): 216–219. DOI:10.3778/j.issn.1002-8331.2010.10.067 |
| [17] | 涂伟, 李清泉, 方志祥. 基于网络Voronoi图的大规模多仓库物流配送路径优化[J]. 测绘学报, 2014, 43(10): 1075–1082. |
| [18] | 佘冰, 叶信岳, 房会会, 等. 基于局部聚类的网络Voronoi图生成方法研究[J]. 地理科学, 2015, 35(5): 637–643. |
| [19] | ASANO T. Aspect-ratio Voronoi Diagram with Applications[C]//International Symposium on Voronoi Diagrams in Science and Engineering. [S. l. ]: IEEE, 2006: 32-39. http://dl.acm.org/citation.cfm?id=1154612 |
| [20] | ASANO T, TAMAKI H. Angular Voronoi Diagram with Applications[C]//International Symposium on Voronoi Diagrams in Science and Engineering. Banff, Canada: [s. n. ], 2006: 18-24. http://dl.acm.org/citation.cfm?id=1153926.1154608 |
| [21] | REILLY W J. The Law of Retail Gravitation[M]. New York: Knickerbocker Press, 1931. |
| [22] | 胡鹏, 杨传勇, 胡海, 等. GIS的基本理论问题-地图代数的空间观[J]. 武汉大学学报(信息科学版), 2002, 27(6): 616–621. |


