2. 中南大学地理信息系, 湖南 长沙 410083
2. Department of Geo-informatics, Central South University, Changsha 410083, China
据统计,2015年中国南方地区共出现5次区域性暴雨过程,造成全国15个省(自治区、直辖市)123.6万人次受灾,近3000间房屋倒塌,1.2万间不同程度损坏,农作物受灾面积5.86×104 hm2。因此,洪涝和地质灾害已成为中国公众及政府部门重点关注的问题。但目前我国山区的气象站和雨量站多设在河谷低处,在海拔较高的地方雨量测点很少。利用如今分布的站点观测资料计算山区的面雨量,是很不可靠的[1]。
目前,已有大量对降雨量空间分布模拟的研究,主要有以下两个方向:①数学建模方法:傅抱璞[1]提出了一个表示降水与地形、海拔高度关系的数学模型;MarquíNez等[2]利用回归模型分析了西班牙北部区域降水和一系列地形变量的关系;Naoum等[3]建立了希腊Crete岛的年降雨多元线性回归模型;Boni等[4]采用多元线性回归方法分析了降雨与气候、地形因子的关系;彭晓芬等[5]通过研究对比发现回归模型模拟方法适用于云南地区的空间模拟,但线性回归模型并不适应于降雨量这种随时间呈某种变化趋势的非平稳随机过程[6]。②空间插值方法:白江涛等[7]发现协同克里金插值方法更适合于降雨量空间分布模拟;何红艳等[8]采用5种插值方法对青藏高原及其周边地区降雨量进行了模拟;Delbari等[9]利用多种插值方法对伊朗地区进行了降雨量空间分布研究;SHEN Zhenyao等[10]采用了两种克里金法对降雨量进行空间插值方法比较。上述方法共有的缺点在于误差较大,不同地区所适用的插值方法不同,甚至同一地区也无法用同一种插值模型进行模拟。
Brunsdon和Fotheringham等提出的地理加权回归(geographic weighted regression, GWR)模型是一种局部加权回归模型[11-12],可以模拟地理现象局部特征,但往往会因为异常值或“弱数据”的出现而对局部参数估计产生较大的影响;LeSage提出了贝叶斯地理加权回归(Bayesian geographic weighted regression, BGWR)模型[14-15],可以弥补GWR模型无法处理异常观测值和“弱数据”的不足;Nirmal Subedi等证实了BGWR模型可以有效改进传统的地理加权回归,有助于提高树木或植物群落的空间结构预测精度[16];崔长彬等利用BGWR对河北省136个县市经济影响因素进行了回归分析[17];丁刚等利用BGWR对政府效能对创新能力建设的影响进行了客观评价[18]。但鲜有学者将贝叶斯地理加权回归模型应用于降雨量预测。
因此,本文提出了一种结合吉布斯采样的贝叶斯地理加权回归方法(GBGWR),进行降雨量空间分布模拟。该方法利用GWR模型的空间非平稳性探测能力,解决了如OLS等线性模型对局部地理现象模拟不精确的问题,又将最大后验概率作为先验信息引入GWR模型,弥补GWR模型无法处理异常观测值和“弱数据”的不足。相较于传统回归分析,本文提出的GBGWR方法能够更好地进行降雨量空间分布模拟。
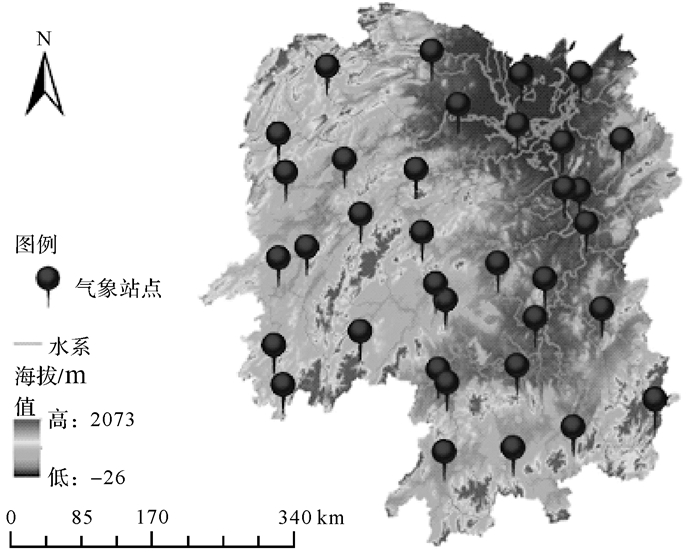
1 研究区和数据 1.1 研究区概况湖南省地处我国腹地,全省地势东高西低,处于云贵高原与江汉平原的过渡地带,地貌形态复杂多样,属于典型的亚热带季风气候区,处在东南季风和西南季风相交的地带,降水分布不均匀,年际变化较大,旱涝灾害发生频率高。因此,本文选择湖南省作为试验区域,对其进行降水空间分布进行模拟。
1.2 数据本文采用的试验数据分别为:①中国气象科学数据共享网(data.cma.cn)提供的湖南省35个监测站点1985—2015年的月值气象观测资料,对于部分缺失数据,首先采用MarquíNez等的数据不完整站点和完整站点之间的回归方程法,对降雨数据进行插补延长,最终整理得到湖南省降雨量及其相关因子30年的持续观测数据,时间分辨率为每月。表 1 给出了降雨量以及相关变量说明。
| 变量名称 | 类型 | 单位 |
| 降雨量 | 因变量 | mm |
| 平均最高温 | 自变量 | 0.1℃ |
| 平均气温 | 自变量 | 0.1℃ |
| 平均风速 | 自变量 | 0.1 m/s |
| 平均水汽压 | 自变量 | 0.1 hPa |
| 高程 | 自变量 | m |
|
| 图 1 研究区站点分布 |
GBGWR模型相较于GWR模型的优点在于不仅可以将地理位置纳入模型之中,而且能够通过将参数的先验信息融入模型来消除或减少异常值对模型的影响,表述为
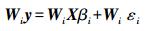 (1)
(1) 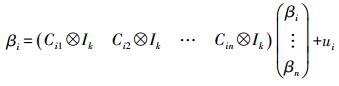 (2)
(2) 式中,Wi代表大小为n×n的基于距离的权重矩阵;y代表空间中n个数据采样点上大小为n×1的因变量矩阵;X代表大小为n×p的解释变量矩阵;βi代表第i个采样点上的未知参数;εi代表大小为n×1的服从独立同分布N(0,σi2Vi)的误差项,其中,Vi=diag(i1,i2,…,in)是大小为n×n的对角矩阵,它代表了跨空间的一组非常数项方差;项Cij代表归一化的基于距离的权重矩阵,大小为n×n,因此行向量Ci1, Ci2, …, Cin之和为1,且Cii=0;ui是具有δ2作为系数缩放因子的随机变化项,且ui~N(0,σ2δ2X′Wi2X)-1;δ2作为系数βi的量化指标,其大小是随系数βi变化的。若βi较大,则允许其系数估计范围更大,灵活性更高;若βi较小,估计系数之间的差异性将变窄,当δ→0时,βi近似与来自邻近观察的其他βi的距离加权线性组合。当δ→∞时(且Vi=In),为普通地理加权回归(GWR)模型。
2.2 吉布斯采样参数估计是贝叶斯地理加权回归方法中的一个重要步骤,运用吉布斯采样计算参数的后验概率是最常用的方法之一。它从间接的概率分布生成随机样本,而不必计算密度本身,GBGWR的吉布斯采样程序可以归纳如下:
(1) 从参数β(Si)0、σ(Si)0、δ0、V(Si)0、γ0的任意值开始。
(2) 对每一个观测值i=1,2,…,n:
a.从p(β(Si)|δ0,σ(Si)0,V(Si)0,γ0)中抽样出一个β(Si)1;
b.从p(σ(Si)|δ0,V(Si)0,β(Si)1,γ0)中抽样出一个σ(Si)1;
c.从p(V(Si)|δ0,β(Si)1,σ(Si)1,γ0)中抽样出一个V(Si)1。
(3) 使用上述n次循环中的每一次采样值β(Si)1,i=1,2,…,n来更新γ0、γ1的值。
(4) 从p(δ|σ(Si)1,β(Si)1,V(Si)1,γ1)中抽样δ1。
(5) 返回步骤(1),利用更新后的值β(Si)1、σ(Si)1、δ1、V(Si)1、γ1继续进行抽样。
由此可见,该方法主要是通过对每一个观测值的单独迭代来模拟模型参数,通过捕获较大方差得到异常值,并且在估计系数的同时使用加权回归方法和方差的导数作为权重。
2.3 最优带宽的选择带宽的选择对于GBGWR至关重要,传统的GBGWR采用CV交叉验证法来确定带宽。但CV交叉验证及AIC信息准则下的最优带宽并不能适应数据点疏密不均的情况。因此,本文在传统GWR模型的基础上对带宽选择方法进行了改进,采用自适应权函数来确立带宽,从而使得模型不受数据点空间分布形式的影响。其中Rij代表数据点j的序号,第k个临近数据点(Rij=k)的距离dij为带宽。
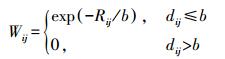 (3)
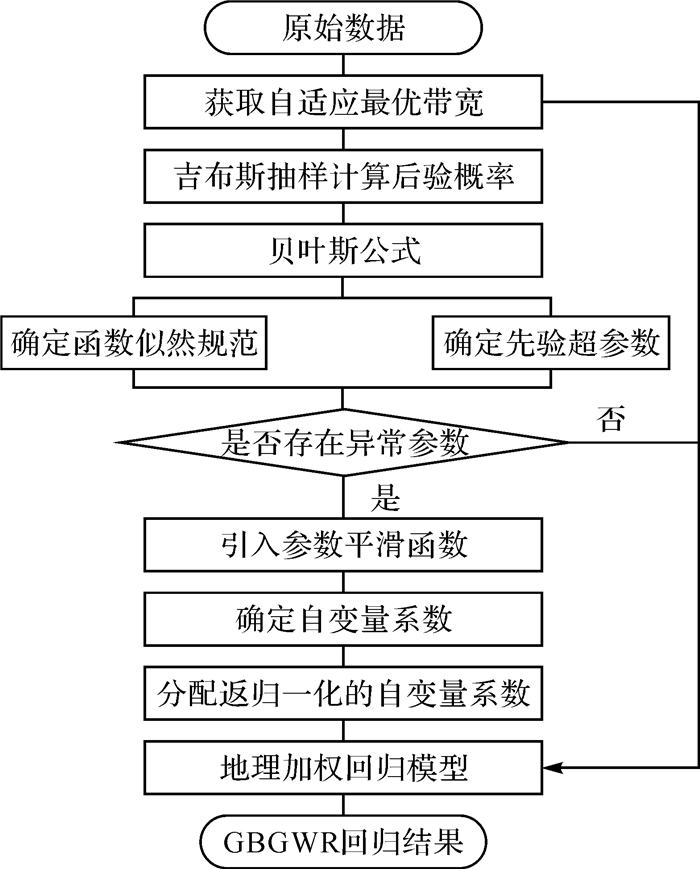
(3) GBGWR模型有两个关键步骤:①采用吉布斯采样方法计算变量的后验概率,并通过贝叶斯公式计算回归变量的先验信息,然后对局部空间内的各个变量进行加权,如若检测出异常观测值,则对该观测值进行降权以降低其对参数估计的影响;②对于“弱数据”问题,通过在贝叶斯模型中引入显式参数平滑关系(如式(2)),对参数变化的空间性质施加限制,最后结合主观先验信息求出系数权重矩阵。其算法流程如图 2所示。
|
| 图 2 算法流程 |
本文分别采用GWR、BGWR及GBGWR 3种方法对湖南省35个监测站点1985—2015年的降雨量观测数据集进行回归,分别从模型系数、模型性能及空间分布模拟3个方面展开对比分析。建模前利用VIF进行多重共线性诊断,结果表明解释变量之间不存在多重共线性,最终建立了如下模型:其中i为数据点编号,β为自变量系数,εi为残差项,R代表降雨量,AMT代表平均最高温,AT代表平均气温,AWS代表平均风速,AVP平均水汽压,E代表高程。
对该模型进行最小二乘估计,主要用于对模型的初步探测,保证后续回归的可行性,同时与GWR、BGWR及GBGWR 3种方法得到的结果进行对比分析,最小二乘估计结果见表 2。
| 变量名 | 系数估计 | t | P>|t| |
| 常量 | -889.815 6 | -3.30 | 0.003 |
| 平均最高温 | 1.133 03 | 0.43 | 0.670 |
| 平均气温 | -4.850 557 | -1.58 | 0.124 |
| 平均风速 | 3.791 793 | 1.60 | 0.120 |
| 平均水汽压 | 16.268 85 | 5.42 | 0.000 |
| 高程 | 0.45 | 4.66 | 0.006 |
| R-squared | 0.794 1 | ||
| Adj R-squared | 0.758 6 |
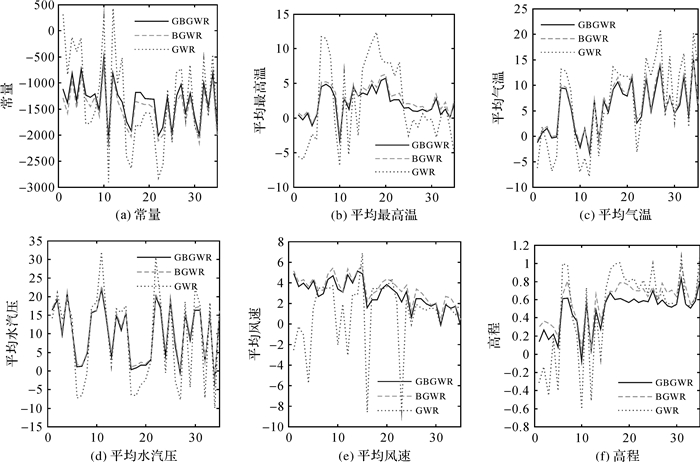
本文所用的GWR、BGWR及GBGWR是根据式(3)中提出的指数距离衰减函数产生的,使用式(2)中提出的一阶邻接先验调整关系进行参数调整,以此减少估计偏差。两种方法得到的回归系数(如图 3所示),通过在单一图表中表示的3种方法对35个监测站点的估计值可以看出:①贝叶斯先验信息对空间平滑的影响主要是通过限制每个监测站点的系数与邻近监测站点的系数相似。②如果35个监测站点的GBGWR估计值及BGWR估计值与GWR估计值有很大的偏差,那么表明贝叶斯先前的信息在估计中引入了大量的偏差。但从图中可以看出,3种方法得到的常数项值估计值均在-890左右变化,平均最高温在1.1左右变化,平均气温在-4.9左右变化,平均风速在3.8左右变化,平均水汽压在16.3左右变化,高程在0.45左右变化,即均接近于最小二乘估计值,GBGWR估计和BGWR估计只是GWR估计的平滑版本,则表明先前的信息有助于强化对异常值的估计和非恒定方差。③基于吉布斯采样的贝叶斯地理加权回归结果与贝叶斯地理加权回归结果整体上一致,表明在小样本的情况下, 不考虑样本规模时, 吉布斯抽样能得到较为正确的后验分布。
|
| 图 3 地理加权回归模型、贝叶斯地理加权回顾模型和基于吉布斯采样的贝叶斯地理加权回归模型估计 |
本文分别计算了3种模型的校正决定系数,结果表明:①GBGWR模型的校正决定系数整体上高于BGWR模型及GWR模型,平均拟合精度达到0.87左右;②GBGWR模型的均方根误差(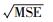
| 方法 | adjR2 | AIC | 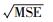 |
| GWR | 0.731 2 | 18.836 9 | 9.511 4 |
| BGWR | 0.810 1 | 10.921 0 | 8.237 6 |
| GBGWR | 0.876 2 | 6.039 4 | 7.914 8 |
| 性能提升(较GWR)/(%) | 19.8 | 67.3 | 16.8 |
| 性能提升(较BGWR)/(%) | 8.2 | 44.7 | 3.9 |
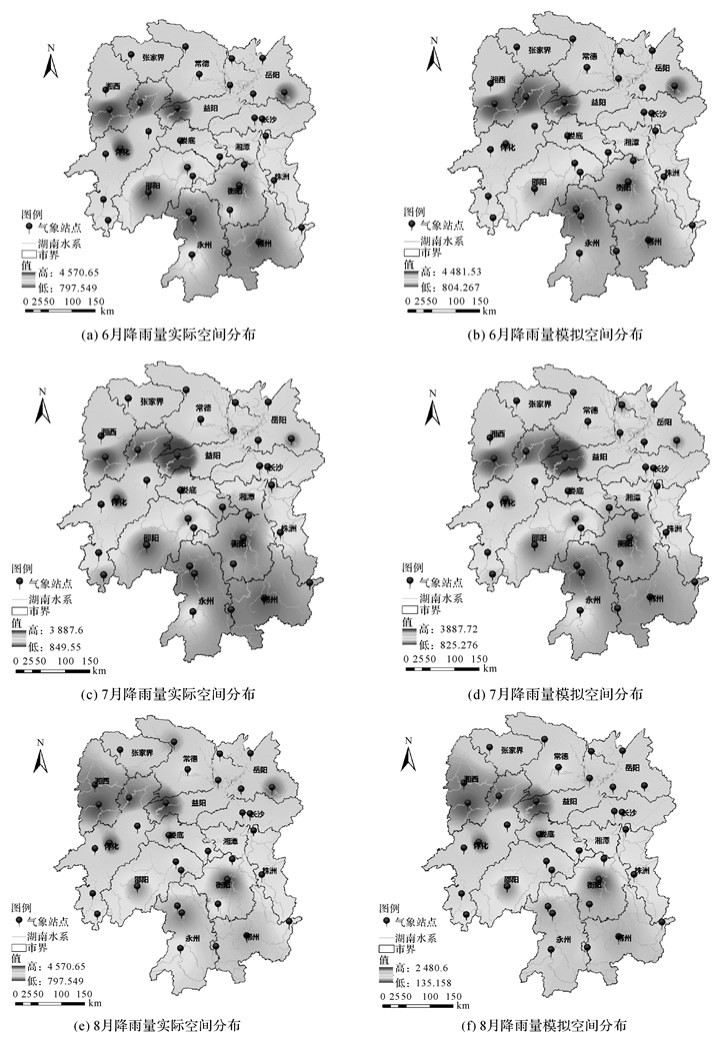
本文分别选取2015年夏季即6—8月湖南省35个监测站点的月均值降雨量数据,采用反距离加权进行插值得到降雨量空间分布图。图 4分别为这3个月湖南省月度降雨量实测值与模拟值空间分布对比图。实测值与模拟值总体呈一致状态,6、7、8三个月份的降雨量空间分布也总体程一致状态。从图中可以看出,降雨量在空间上主要呈现北高南低,从北向南依次降低的特征,中部地区有一条明显的绿色条带将湖南省分为南中北3个降水量区域;其次,湖南省的降雨分布主要与大气环流和地形有关,邵阳、衡阳等地降雨量明显低于其他地区,主要原因在于衡邵盆地6—8月受西太平洋副热带高压的控制,表现出长时间的晴热干燥天气,同时由于其处于南岭北侧,为东南季风的背风区,易产生焚风效应;从时间上来看,每年夏季6月为一年中平均降水量最大的月份,之后依次递减,但总体趋势呈现一致的状态。
|
| 图 4 2015年湖南省降雨量空间分布实际与模拟对比 |
本文使用GWR模型、BGWR模型及GBGWR对湖南省35个监测站点30年的降雨量数据进行空间分布模拟,相较于GWR和BGWR,GBGWR很好地结合了贝叶斯理论与地理加权回归二者的优点,尤其是对于降雨量监测站点稀疏、空间分布不均、降雨量的不稳定性有着良好的适用性。试验表明,该方法对于降雨量的空间分布模拟具有更好的稳健性和更佳的模拟效果。综上所述,得出如下结论:
(1) 湖南省夏季的降雨量整体上表现为北高南低、由南往北依次减少的分布特征,且降雨量越大时空间分布上的差异越大。
(2) GBGWR模型的平均拟合优度达到了0.87,远高于GWR模型的0.73和BGWR模型的0.81,主要原因在于在小样本的情况下, 不考虑样本规模时, 吉布斯抽样能得到较为正确的后验分布。同时GBGWR模型估计系数对异常值敏感。当邻域中存在异常值时,GWR方法需要通过剔除异常值重新建立模型。相比之下,GBGWR可以自动识别异常值,并且通过降低异常值权重来减少异常值的影响,并且得到的估计系数是稳健的。
由于降雨量随着地形和季节变化的波动性较大[19],因此下一步的研究工作主要集中在GBGWR模型的基础上纳入地形因素和时间因素,从贝叶斯时空地理加权的角度进一步优化模型。
| [1] | 傅抱璞. 地形和海拔高度对降水的影响[J]. 地理学报, 1992(4): 302–314. |
| [2] | MARQUÍNEZ J, LASTRA J, GARCÍA P. Estimation Models for Precipitation in Mountainous Regions:The Use of GIS and Multivariate Analysis[J]. Journal of Hydrology, 2003, 270(1-2): 1–11. DOI:10.1016/S0022-1694(02)00110-5 |
| [3] | NAOUM S, TSANIS I K. A Multiple Linear Regression GIS Module Using Spatial Variables to Model Orographic Rainfall[J]. Journal of Hydroinformatics, 2004, 6(1): 39–56. |
| [4] | BONI G, PARODI A, SICCARDI F. A New Parsimonious Methodology of Mapping the Spatial Variability of Annual Maximum Rainfall in Mountainous Environments[J]. Journal of Hydrometeorology, 2007, 9(3): 492–506. |
| [5] | 彭晓芬, 黄甫则, 周汝良. 云南省年均降雨量空间插值模拟方法比较[J]. 西南林业大学学报, 2010, 30(5): 25–28. |
| [6] | 张书文, 李占甫. 时间序列分析在预测年降水量中的应用[J]. 水资源研究, 1996(4): 7–11. |
| [7] | 白江涛, 白建军, 王磊, 等. 基于GIS的关中——陕南地区降雨量空间插值分析[J]. 安徽农业科学, 2011, 39(33): 20872–20876. DOI:10.3969/j.issn.0517-6611.2011.33.204 |
| [8] | 何红艳, 郭志华, 肖文发, 等. 利用GIS和多变量分析估算青藏高原月降水[J]. 生态学报, 2005, 25(11): 2933–2938. DOI:10.3321/j.issn:1000-0933.2005.11.020 |
| [9] | DELBARI M, AFRASIAB P, JAHANI S, et al. Spatial Interpolation of Monthly and Annual Rainfall in Northeast of Iran[J]. Meteorology & Atmospheric Physics, 2013, 122(1-2): 103–113. |
| [10] | SHEN Z, CHEN L, LIAO Q, et al. Impact of Spatial Rainfall Variability on Hydrology and Nonpoint Source Pollution Modeling[J]. Journal of Hydrology, 2012, s 472-473(24): 205–215. |
| [11] | 覃文忠, 王建梅, 刘妙龙. 地理加权回归分析空间数据的空间非平稳性[J]. 辽宁师范大学学报(自然科学版), 2005, 28(4): 476–479. |
| [12] | BRUNSDON C. Geographically Weighted Reg Ression:A Method for Exploring Spatial Nonstation Arity[J]. Geographical Analysis, 1996, 28(4): 281–298. |
| [13] | 武文娟, 徐京华, 时进, 等. 基于GWR的四川省医院床位数时空分布及其影响因素研究[J]. 测绘通报, 2016(4): 49–53. |
| [14] | LESAGE J P. A Spatial Econometric Examination of China's Economic Growth[J]. Geographic Information Sciences, 1999, 5(2): 143–153. |
| [15] | LESAGE J P. A Family of Geographically Weighted Regression Models[C]//Advances in Spatial Econometrics. Berlin Heidelberg: Springer, 2004: 241-264. https://link.springer.com/chapter/10.1007/978-3-662-05617-2_11 |
| [16] | SUBEDI N. Local Modeling of Tree Crown Area Using Bayesian Geographically Weighted Regression[D]. [S. l. ]: State University of New York College of Environmental Science and Forestry, 2012. |
| [17] | 崔长彬, 姜石良, 张正河. 河北县域经济影响因素的空间差异分析——基于贝叶斯地理加权回归方法[J]. 经济地理, 2012, 32(2): 39–45. |
| [18] | 丁刚. 基于BGWR模型的区域创新能力建设中政府效能测评[J]. 技术经济, 2013, 32(4): 20–26. |
| [19] | 叶金桃, 王俊超, 冯光柳, 等. 降雨型滑坡联合监测及预警预报系统研究[J]. 测绘通报, 2012(2): 31–34. |