2. 武汉大学地理信息系统教育部国家重点实验室, 湖北 武汉 430079;
3. 数字制图与国土信息应用工程国家测绘地理信息局重点实验室, 湖北 武汉 430079
2. Key Laboratory of Geographic Information System, Ministry of Education, Wuhan University, Wuhan 430079, China;
3. Key Laboratory of Digital Mapping and Land Information Application Engineering, National Administration of Surveying, Mapping and Geoinformation, Wuhan University, Wuhan 430079, China
多时相遥感影像变化检测是指对不同时间、同一地区的影像数据进行分析从而得到地表变化信息的过程[1]。近些年随着遥感资源数据的丰富,遥感影像变化检测技术已经在土地动态检测、森林植被变化、城市扩展和灾害监测等诸多领域发挥着积极和重要的作用,是遥感技术应用领域的一个重要方向。但是到目前为止还没有一种稳健的算法能够适用大多情况,因此,发展可靠、稳定的算法仍然是研究热点[2]。
根据是否利用样本先验知识可以将变化检测方法分为3类:①非监督变化检测;②基于监督方法的变化检测;③半监督变化检测。目前非监督变化检测主要分为两类:一是利用从影像提取的特征进行聚类,如Ghosh A[3]根据影像光谱特征,利用模糊聚类(FCM)和GKC聚类的方式进行变化检测,由于只采用一种光谱特征信息且没有考虑像素的位置关系,因此对噪声抑制不明显;P Khandelwal[4]首先进行了多光谱影像数据的特征融合,然后采用Kohonen网络进行非监督聚类,同样没有考虑像素的空间邻域信息,造成虚警率较高。二是根据影像特征进行建模,利用贝叶斯决策的最小错误率准则等进行变化检测,如狄亚南等[5]认为变化像元和未变化像元服从高斯分布,联合变化强度和相关系数进行最小错分概率的阈值优化;Celik T[6]采用高斯混合模型(GMM)对差异影像建模,然后结合最大期望值算法(EM算法)和贝叶斯决策得到变化检测结果;但是由于像元的分布不一定服从某一种特定的分布,而且对模型参数的估计会存在不同程度的误差,因此结果也有很大的偶然性。基于监督学习的方法主要有后分类的变化检测、神经网络法和支持向量机(support vector machine,SVM)法等,如郝睿等[7]从影像的直方图统计量作为依据,采用基于BP神经网络的方法,通过选取适当的样本点来进行土地利用变换检测;徐俊峰[8]利用高分辨率影像的多种特征,通过训练SVM分类器来进行变化检测,同样需要手动添加样本点。半监督学习的变化检测则是利用少量标记的样本,结合整体数据分布特征进行变化像素的提取[9]。后两种方法都需要对含有变化信息的样本进行训练,但是实际中获得较多的样本往往很难,而且样本质量的高低会直接影响到变化检测结果,因此非监督的变化检测仍然是目前的主流算法。
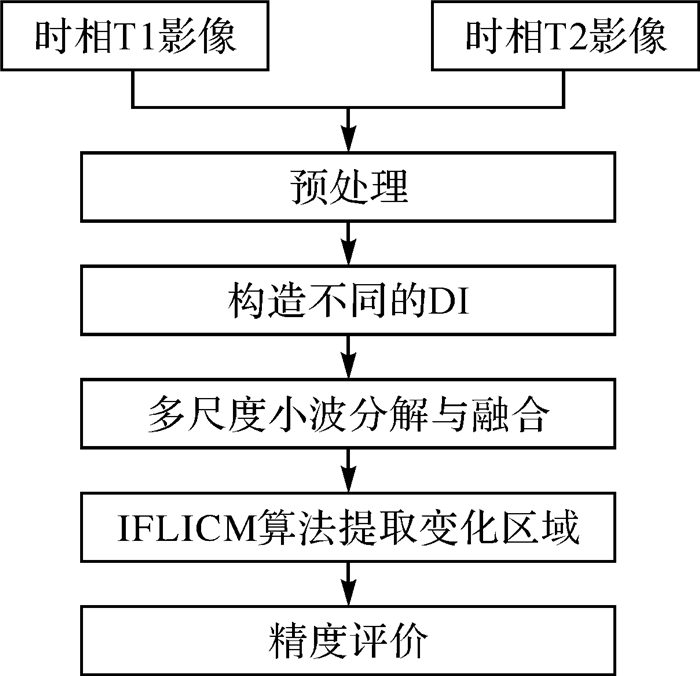
针对上述问题,本文提出一种基于小波融合与改进的模糊聚类非监督算法。首先运用代数运算法和变化矢量分析法构造差异影像,然后利用小波分解的方法将影像分为多层;对多层影像采用一种新的融合策略,以保证差异图既能含有变化区域的边界信息,又能一定程度上抑制噪声;最后对融合后的差异图用改进的IFLICM(improved fuzzy local information clustering means)算法进行变化检测。以2组多光谱影像为例,首先将融合前后的差异影像进行对比试验,然后再以融合后的数据进行模糊聚类系列算法的分析。算法的流程如图 1所示。
|
| 图 1 变化检测流程 |
首先利用差值法和变化矢量分析法从多光谱影像数据中提取两种不同的差异图,分别记为IADI和ICVA,二者的计算方法如下
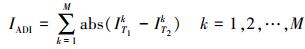 (1)
(1) 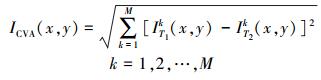 (2)
(2) 式中,IT1k和IT2k分别表示T1时刻和T2时刻第k波段的光谱灰度值;M表示多光谱影像的波段数;IADI能够很好地反映出变化区域的轮廓,但是对噪声敏感;ICVA则是突出变化区域的整体分布,有一定的抗噪性但是边缘轮廓模糊。因此本文采用一种小波融合的策略,采用离散小波变换(DWT)小波多尺度分解和融合的方式获得差异影像,使得融合后的结果既有一定的抗噪性,又能很好地突出变化区域的轮廓。首先将二者进行N层小波分解,对各层系数实施以下融合策略
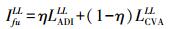 (3)
(3) 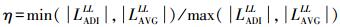 (4)
(4) 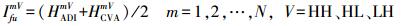 (5)
(5) 式中,IfuLL表示融合后的影像的低频系数;η和(1-η)分别表示ADI和CVA的低频分量所占的权重;LADILL和LCVALL分别表示IADI和ICVA第N层小波系数的低频部分;LAVGLL则表示二者的平均值;HADIm和HCVAm分别表示第m层3个方向高频系数;Ifum表示融合后影像的高频系数。
小波域融合的具体流程如图 2所示。

|
| 图 2 小波域融合流程 |
模糊聚类分析是指根据研究对象本身的属性来构造模糊矩阵,并在此基础上根据一定的隶属度来确定聚类关系,从而客观且准确地进行聚类。相比于硬聚类,模糊聚类更能体现出分割的优势。传统的模糊聚类算法(fuzzy clustering means,FCM),通过计算目标函数Jm的最小值,得到隶属度矩阵和数据中心点的迭代公式
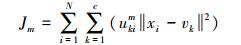 (6)
(6) 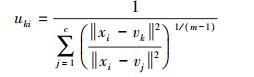 (7)
(7) 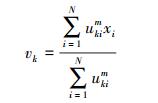 (8)
(8) 式中,N为总的像元数;c表示类别数(本文试验中取2);uki表示第i个点属于k类的隶属度;vk表示第k类的聚类中心;m为模糊度(一般取2)。
在对差异影像进行分割时没有考虑像元的空间位置关系,并且算法的复杂度高、计算量大,因此近些年很多学者在利用FCM进行影像分割时,在原算法的基础上进行了改进。Szilagyi提出了EnFCM算法,加快了影像的聚类过程,通过对像素点及其8邻域像素的线性加权求和预处理原图像,形成了从原始图像到其局部邻域像素的平均图像,并且还采用灰度编码的方式进行迭代,使执行时间明显减少。S Krinidis[10]提出了模糊局部信息聚类算法(fuzzy local information clustering means,FLICM),该算法结合灰度级信息和局部空间信息,并且在聚类的过程中引入模糊因子
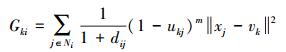 (9)
(9) 式中,Gki表示第i个元素属于第k类的模糊因子;Ni表示第i个点的邻域集合;dij为点i到点j之间的欧氏距离;vk为第k类的聚类中心。从式(9)可以看出,Gki不需要依赖其他参数,而且仅仅与像元的k阶邻域有关,dij越大,表明邻域点对中心像元点的影响越小。因此新的目标函数如下
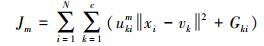 (10)
(10) 根据拉格朗日乘数法求得新的隶属度和聚类中心的迭代公式如下
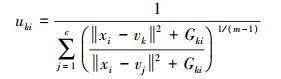 (11)
(11) 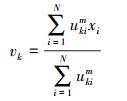 (12)
(12) 考虑到像元之间的相互影响程度并不是线性的,而是更加普遍的高斯分布,并且还应该与像素的相对大小有关,即像元差值越大,对中心像元的影响越大。因此本文对模糊因子作出了调整,提出了一种改进的模糊局部信息聚类算法(improved fuzzy local information clustering means,IFLICM)。通过引入高斯函数,以核空间的距离代替欧氏距离来进行求解,即
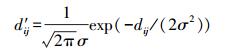 (13)
(13) 同时考虑像元的相对大小,利用邻域像素和窗口的标准差进行表示,即
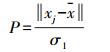 (14)
(14) 式中,σ1为窗口像素值的标准差;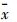
故改进的模糊因子为
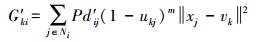 (15)
(15) 将新的距离公式代入式(10)即为新的迭代公式。因此新的算法流程为:
(1) 给m、σ、ε和c设置初始值(本文σ取1,m取2)。
(2) 随机初始化隶属度矩阵ukj,设置最大迭代次数M。
(3) 利用式(12)计算各类的聚类中心vk。
(4) 将式(13)和式(15)代入式(11)求解uki。
(5) 计算max{Jm(b)-Jm(b+1)} < ε则迭代结束;否则返回步骤(3)。
3 试验与分析 3.1 试验数据与平台试验采用的第1组数据为Landsat 7提供的2006年5月和2010年7月咸海地区的中低分辨率多光谱遥感影像。经过影像的辐射矫正和配准后(配准后的误差小于0.5像素),截取长和宽各300像素区域;第2组试验区域为郑州某高校校区高分辨率影像,分别拍摄于2012年5月和2016年4月,长为300像素,宽为200像素,为高分辨率影像。试验平台为Matlab R2016b。从第1组数据目视解译可以很直观地看出,这4年里咸海的面积大幅度缩减,水位不断下降,周围小湖泊的面积也在减少;第2组数据许多建筑物也在发生变化。影像数据和参考变化图如图 3所示。

|
| 图 3 试验影像数据及参考图 |
为了验证算法的有效性,本文给出两组试验:一是采用融合前后的差异影像分别进行试验,分别采用EM算法[11]、PCAKmeans[12]和经典的FCM算法验证其融合算法的有效性;二是用融合后的影像分别用不同的聚类算法(EnFCM[13]、FLICM[14]、IFLICM)进行试验,验证本文提出的IFLICM算法的有效性。
3.2 试验结果与分析(1) 首先以ADI、CVA和融合后的影像(记为FUS)分别采用不同的算法进行试验,第1组如图 4、表 1所示,第2组如图 5、表 2所示。

|
| 图 4 数据1得到的结果 |
| 算法类型 | 差异影像 | 虚警数 | 漏检数 | 正确率/(%) | Kappa系数 |
| EM算法 | ADI | 4868 | 931 | 93.55 | 0.621 |
| CVA | 3359 | 1860 | 94.20 | 0.607 | |
| FUS | 718 | 1667 | 97.35 | 0.779 | |
| PCAKmeans | ADI | 3517 | 192 | 95.87 | 0.748 |
| CVA | 2669 | 427 | 96.56 | 0.836 | |
| FUS | 2055 | 215 | 97.47 | 0.865 | |
| FCM | ADI | 7179 | 495 | 91.47 | 0.571 |
| CVA | 6475 | 554 | 92.19 | 0.591 | |
| FUS | 3325 | 341 | 95.92 | 0.751 |

|
| 图 5 数据2得到的结果 |
| 算法类型 | 差异影像 | 虚警数 | 漏检数 | 正确率/(%) | Kappa系数 |
| EM算法 | ADI | 6167 | 3141 | 84.48 | 0.522 |
| CVA | 3710 | 4278 | 86.68 | 0.535 | |
| FUS | 4120 | 2439 | 89.07 | 0.561 | |
| PCAKmeans | ADI | 4689 | 2300 | 88.35 | 0.633 |
| CVA | 5478 | 2005 | 87.53 | 0.621 | |
| FUS | 4397 | 2223 | 88.97 | 0.643 | |
| FCM | ADI | 6996 | 2850 | 83.59 | 0.513 |
| CVA | 7556 | 2672 | 82.95 | 0.505 | |
| FUS | 6726 | 2752 | 84.20 | 0.529 |
从第1组试验可以很明显地看出,无论采用EM算法、PCAKmeans还是FCM算法,利用融合后的影像进行变化检测的准确率都有了不同程度的提高(尤其是FCM算法,数据1的虚警的像元数由6803和6104减少到了2904),主要是因为单纯的ADI和CVA都提供了像素值变化的平均信息,因此都会包含很多孤立的像元点,从而造成较大的虚警率,尤其是FCM算法还缺少邻域的操作,故而在进行多尺度小波融合后对影像高频部分进行了非等权的叠加,一定程度地抑制了噪声,提高了正确率;纵向对比可以发现,对于高分辨率影像,由于地物结构精细复杂,并且存在阴影效应,虽然融合后的错误率有所减少,但是整体精度还有待提高。
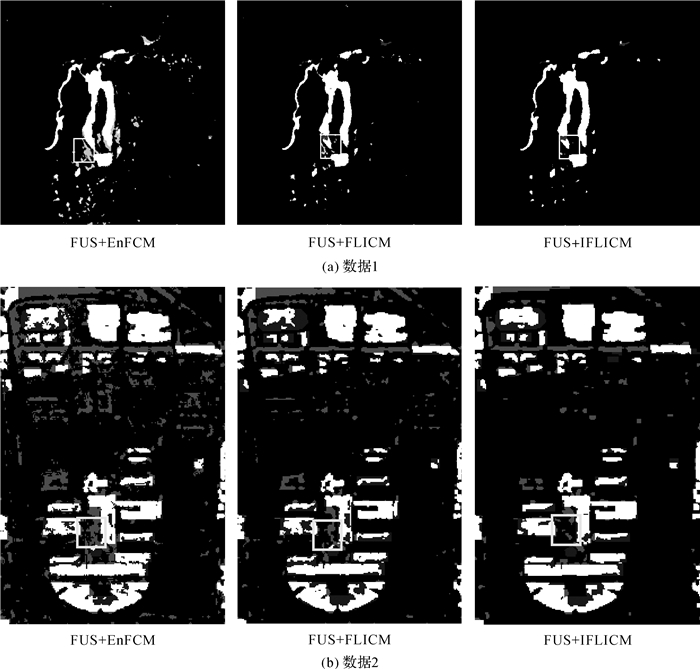
(2) 对融合后的差异影像采用不同的聚类算法进行试验,结果如图 6、表 3所示。
|
| 图 6 不同聚类算法得到的结果 |
| 数据 | 聚类算法 | 虚警数 | 漏检数 | 正确率/(%) | Kappa系数 |
| 数据1 | EnFCM | 2850 | 155 | 96.67 | 0.613 |
| FLICM | 557 | 594 | 98.72 | 0.901 | |
| IFLICM | 140 | 314 | 99.72 | 0.974 | |
| 数据2 | EnFCM | 5990 | 2092 | 86.53 | 0.597 |
| FLICM | 2855 | 3400 | 89.58 | 0.636 | |
| IFLICM | 2157 | 2560 | 92.14 | 0.727 |
从第2组试验结果可以看出,相比于其他模糊聚类算法,本文提出的IFLICM算法在一定程度上提高了变化检测精度。EnFCM虽然对周围邻域进行了线性加权,对噪声有一定的抑制作用,但是该算法是在平均图像的基础上进行的操作,因此对于噪声点比较集中的区域仍然没有效果。FLICM和IFLICM则是在不改变原影像的基础上,通过引入模糊因子来进行考虑的。但是传统的FLICM只是考虑到邻域的点对中心点的影响是线性的,而图像的马尔可夫性则表明,利用高斯分布来描述这种影响更加确切;而且FLICM并没有考虑到像元的相对大小对中心点影响的差异性,因此IFLICM针对噪声比较密集的区域具有更强的抑制效果,虚警的像元数量有了明显的减少。
4 结语本文提出了一种基于小波域融合和改进的模糊局部信息聚类的变化检测方法。通过对不同的差异影像进行多尺度分解,把二者的高频部分进行了非等权叠加来实现去除噪声的目的,最后利用小波逆变换得到新的差异图。试验结果表明,利用融合后的影像再进行变化检测能够较为明显地降低变化检测错误率,提高变化检测的精度。在聚类过程中为了综合利用窗口内像元的邻域信息,提出了一种改进的IFLICM算法,能够充分利用像素的灰度信息和空间位置关系,通过改进模糊因子能够更好地实现抑制非孤立点噪声的影响,提高了变化检测的准确率。但是针对高分辨率影像,由于地物结构复杂精细,地物的“同物异谱”和“同谱异物”效应更加明显,并且由于阴影的存在会造成虚警率较高等问题。虽然改进的算法使得精度有一定的提高,但是对于高分辨率影像如何消除这些影响将会是下一步的研究重点。
| [1] | RADKE R J, ANDRA S, ALKOFAHI O, et al. Image Change Detection Algorithms:A Systematic Survey[J]. IEEE Transactions on Image Processing, 2005, 14(3): 294–307. DOI:10.1109/TIP.2004.838698 |
| [2] | LI D. Remotely Sensed Images and GIS Data Fusion for Automatic Change Detection[J]. International Journal of Image and Data Fusion, 2010, 1(1): 99–108. DOI:10.1080/19479830903562074 |
| [3] | GHOSH A, MISHRA N S, GHOSH S. Fuzzy Clustering Algorithms for Unsupervised Change Detection in Remote Sensing Images[J]. Information Sciences, 2011, 181(4): 699–715. DOI:10.1016/j.ins.2010.10.016 |
| [4] | KHANDELWAL P, SINGH K K, SINGH B K, et al. Unsupervised Change Detection of Multispectral Images Using Wavelet Fusion and Kohonen Clustering Network[J]. International Journal of Engineering & Technology, 2013, 5(2): 1401–1406. |
| [5] | 狄亚南, 江刚武, 张一, 等. 联合变化强度和相关系数最小错分概率变化检测阈值优化[J]. 测绘科学技术学报, 2016, 33(2): 180–184. |
| [6] | CELIK T. Bayesian Change Detection Based on Spatial Sampling and Gaussian Mixture Model[J]. Pattern Recognition Letters, 2011, 32(12): 1635–1642. DOI:10.1016/j.patrec.2011.05.008 |
| [7] | 郝睿, 徐俊峰, 王庆宝, 等. 基于BP神经网络的多特征融合变化检测方法[J]. 海洋测绘, 2016, 36(1): 79–82. |
| [8] | 徐俊峰, 张保明, 郭海涛, 等. 一种多特征融合的面向对象多源遥感影像变化检测方法[J]. 测绘科学技术学报, 2015, 32(5): 505–509. |
| [9] | SHAO P, SHI W, HE P, et al. Novel Approach to Unsupervised Change Detection Based on a Robust Semi-supervised FCM Clustering Algorithm[J]. Remote Sensing, 2016, 8(3): 264. DOI:10.3390/rs8030264 |
| [10] | KRINIDIS S, CHATZIS V. A Robust Fuzzy Local Information C-means Clustering Algorithm. [J]. IEEE Transactions on Image Processing, 2010, 19(5): 1328-1337. https://dl.acm.org/citation.cfm?id=1852198 |
| [11] | BRUZZONE L, PRIETO D F. Automatic Analysis of the Difference Image for Unsupervised Change Detection[J]. IEEE Transactions on Geoscience & Remote Sensing, 2000, 38(3): 1171–1182. |
| [12] | CELIK T. Unsupervised Change Detection in Satellite Images Using Principal Component Analysis and k-Means Clustering[J]. IEEE Geoscience & Remote Sensing Letters, 2009, 6(4): 772–776. |
| [13] | SZILAGYI L, BENYO Z, SZILAGYI S M, et al. MR Brain Image Segmentation Using an Enhanced Fuzzy C-means Algorithm[C]//Proceedings of the 25th Annual International Conference of the IEEE. [S. l. ]: IEEE, 2003: 724-726. http://ieeexplore.ieee.org/document/1279866/ |
| [14] | KRINIDIS S, CHATZIS V. A Robust Fuzzy Local Information C-Means Clustering Algorithm[J]. IEEE Transactions on Image Processing, 2010, 19(5): 1328–1337. DOI:10.1109/TIP.2010.2040763 |


