2. 武汉市测绘研究院, 湖北 武汉 430022;
3. 西安测绘总站, 陕西 西安 710054
2. Wuhan Geomatic Institute, Wuhan 430022, China;
3. Xi'an Information Technique Institute of Surveying and Mapping, Xi'an 710054, China
实时监测流行病的传播和分布能够为公共卫生部门进行决策提供科学参考,进而控制其传播范围和影响力度。作为有效的分析及可视化工具,GIS在空间流行病学领域发挥着越来越大的作用[1]。GIS数据来源丰富,除了官方权威部门采集的数据,也有由大量非专业人员志愿获取的,被称为众源地理数据[2],其中就包括了带有位置信息的搜索引擎数据,这是一种典型的时空大数据,它具备的泛在性、高时效性使得其在挖掘社会现象时空规律、发现空间模式特征、预测时空演变规律方面具有重要作用[3]。
各国现有流感监控方法主要是汇总哨点医院上报的流感样病例(ILI),虽然结果准确,但时间上有延迟,如中国国家流感中心发布的流感周报一般有1~2周延迟[4]。因此,许多新方法应用到了流感快速监测中,如根据电话咨询量、药物销量、学校和企业缺席人数来推测流感发病率[5]。自从Ginsberg等利用Google的搜索数据来探测流感流行趋势[6]以来,国内外越来越多的科研工作者将互联网的搜索引擎、社交网络和网络新闻媒体这3类大数据应用到流感监测中。处理以上数据使用的方法主要包括多元回归分析及支持向量机、人工神经网络等机器学习方法,其中回归分析仍然是应用广泛且效果较好的方法之一[7]。
过往的研究主要以发病数的时间序列为研究对象,关注研究区域整体的发病情况,而对于研究区域内部空间分布的研究较少,没有充分利用大数据中包含的空间信息。本文在多元回归分析的基础上,使用时空地理加权回归(geographically and temporally weighted regression, GTWR)进行建模,充分利用搜索引擎数据中的位置信息,试图构造能更好模拟我国流感空间分布的模型,为空间流行病学研究和公共卫生决策提供支持。
1 模型与方法 1.1 最小二乘线性回归模型OLS模型是最基本的回归方法,也是所有空间回归分析的正确起点。它适用于回归关系具有全局空间稳定性的情况[8],可为变量或过程提供一个全局模型,用唯一的回归方程表示为
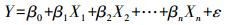 (1)
(1) 式中,Y为因变量,表示实际发病数;X1到Xn为解释变量,表示关键词的搜索指数;β为回归系数,表示对应的解释变量与因变量之间关联强度和类型;ε为随机误差项。若回归残差在统计上呈现明显的空间自相关,OLS回归的结果不可靠,需要使用局部回归方法来提高模型稳定性。
1.2 地理加权回归模型若流感发病数与关键词百度指数之间的关系存在空间非平稳性,则模型中变量的关系是基于空间位置的函数。GWR模型可为变量或过程提供局部模型,能够有效探测空间非平稳特征[9],它对每个目标要素带宽范围内的要素进行参数估计,通过引入地理加权函数对式(1)进行扩展,模型可表示为
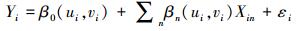 (2)
(2) 式中,(ui, vi)表示第i个目标要素的坐标;β0(ui, vi)为第i个目标要素的截距常量;βn(u, v)为连续函数;βn(ui, vi)为该函数在i点的值。
本文使用高斯函数作为GWR模型的空间核函数。带宽的选择对GWR模型有较大影响,它的形状和范围取决于核类型、带宽方法等参数,本文使用固定核宽,根据模型的赤池信息准则(Akaike information criterion,AIC)来确定最优带宽。
1.3 时空地理加权回归模型除了空间因素外,时间因素也可能导致流感发病数与关键词百度指数的关系呈现非平稳性,时空地理加权回归能够有效解决回归模型中无法同时考虑时间和空间异质性的问题[10]。它使用三维坐标来定义时空位置,相应地,式(2)可扩展为
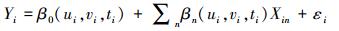 (3)
(3) 式中,(ui, vi, ti)为第i个目标要素的三维坐标;β0(ui, vi, ti)为该要素对应的截距常量;βn(u, v, t)为连续函数,βn(ui, vi, ti)为该函数在i点的值。采用局部加权最小二乘估计可计算出参数的估计值为
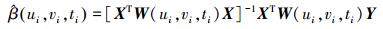 (4)
(4) 式中,W(ui, vi, ti)=diag(αi1, αi2, …, αin)表示n阶时空距离权重对角矩阵(n为样本数);对角元素αij(1≤j≤n)表示点j对观测点i的影响,它与时空距离有关。点j到观测点i的时空距离越近,对估计结果的影响越大。因此,与GWR模型相似,时空距离衰减函数直接影响参数的估计,本文中GTWR模型同样使用高斯核函数。由于位置和时间使用不同的单位系统来计量,它们的尺度效应也不相同,因此引入椭圆坐标系统来表示时空距离[11],在给定空间距离dS和时间距离dT的情况下,时空距离表示为
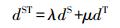 (5)
(5) 式中,λ和μ分别为平衡空间距离和时间距离的比例因子,选择合适的值后dST就能度量时空距离。设k=μ/λ,若k为0,GTWR模型就简化为GWR模型,若k为无穷大,模型将简化为时间加权回归模型(TWR)。具体的时空距离比例因子和最优带宽通过计算AIC值使其达到最小来确定。
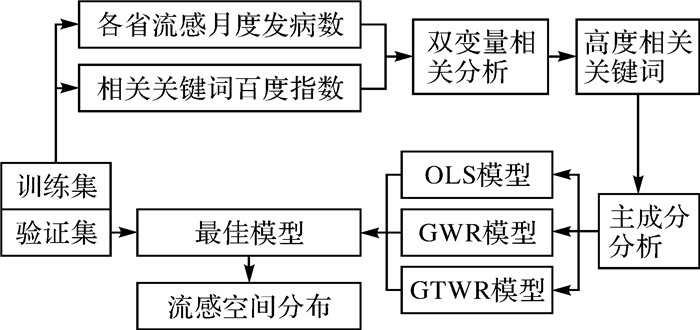
1.4 技术路线本文的试验数据包含训练集和验证集两部分。在对训练集中的发病数和相关关键词的搜索指数进行双变量相关分析的基础上,筛选出与流感发病显著相关的关键词。通过构建OLS模型并观察VIF值(方差膨胀因子)来检验自变量之间的共线性,利用主成分分析法消除共线性以降低模型估计误差。再采用消除共线性后的主成分作为自变量,分别使用OLS、GWR和GTWR构建流感空间分布模型,最后对以上回归分析方法的模拟结果进行精度验证和对比。将验证集的自变量代入拟合效果最佳的模型中,得到各省流感发病数的预测值,与实际分布情况进行对比验证。技术路线如图 1所示。
|
| 图 1 技术路线 |
本文使用流感官方发病数据作为模拟目标,数据来源于公共卫生科学数据中心(http://www.phsciencedata.cn/Share/index.jsp),样本采集时间范围为2013年10月至2014年3月,统计全国范围各省各月的流感发病数量,由于香港、澳门、台湾、西藏的数据难以获取,下文的分析中将不包括上述地区。将以上时间范围和地点的流感相关关键词的搜索量作为自变量,已有的国内外相关研究大多使用谷歌趋势作为数据源,但百度占据了中国84.5%以上的份额[12],因此本文使用的搜索引擎数据来自于百度指数网站(https://index.baidu.com/)。
以上试验数据被划分为训练集和验证集两个部分,在模型建立阶段均选取2013年10月至2014年2月的试验数据作为模型训练样本,用于估计回归参数,使用2014年3月的试验数据作为验证集,用于对模型模拟流感空间分布的效果进行验证。
2.2 关键词选取不同关键词在某一特定时间地点对应不同的搜索频率,它的选取直接影响模型结果,因此必须选择与流感发病高度相关的关键词。本文选取的关键词的百度指数与流感发病数的相关系数大于0.5,并且要求关键词在语义上与流感相关。若同时受到其他变量的影响,与流感无关的关键词也可能与发病数有很高的相关系数。Ginsberg等从五千万个搜索词中选取了相关系数最高的45个,计算量过大,不具有可重复性。以往的研究表明,越多的关键词不能保证越高的模型拟合度,对于一个相对精确的模型,增加一个关键词的边际贡献并不显著,反而增大了计算量[13]。依据以上原则,结合相关文献[4, 12-13]选取了咳嗽、发烧、喉咙痛、H7N9、头痛、肺炎、感冒、禽流感、流感、甲流、流感症状、流感病毒、流鼻涕等13个关键词,分别用X1至X13表示,以上关键词的百度指数均在0.01水平上与流感发病数显著相关,具体的相关系数见表 1。
| 关键词 | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | X11 | X12 | X13 |
| 相关系数 | 0.729 | 0.725 | 0.701 | 0.698 | 0.654 | 0.650 | 0.642 | 0.641 | 0.634 | 0.608 | 0.571 | 0.536 | 0.514 |
使用X1至X13作为解释变量,发病数Y作为因变量,利用普通最小二乘法(OLS)建立流感空间分布模型,再通过观察VIF值检验自变量之间的共线性。模型校正后的R2值为0.688,说明该模型整体拟合效果较好。但是各解释变量对应的VIF值较大,最小值为8.167,最大达到68.366。一般认为VIF值大于7.5是变量间共线性的触发点[14],该模型解释变量的组合存在冗余,这会导致模型变得不可靠,因此需要通过降低解释变量维度来消除共线性,进而减少模型估计误差。
对关键词的百度指数X1至X13运行主成分分析,所有关键词的共同度均大于0.6,根据特征值大于1的准则可提取3个主成分,分别用PC1、PC2、PC3表示,其累积方差贡献率为82.76%,可较好地代表原始数据。
3 流感空间分布模型 3.1 基于OLS的空间分布模型使用消除共线性后的3个主成分作为自变量,流感发病数作为因变量,进行OLS多元线性回归,得到模型参数估计值及模型统计诊断结果见表 2。
| 变量 | 系数 | 标准误差 | t检验值 | VIF |
| 截距 | 760.617 | 43.681 | 17.413 | — |
| PC1 | 778.238 | 43.802 | 17.767 | 1.001 |
| PC2 | 482.641 | 43.802 | 11.019 | 1.000 |
| PC3 | 391.013 | 43.802 | 8.927 | 1.001 |
| 调整R2 | 0.737 | |||
| AIC | 2 313.12 | |||
| RSS(108) | 4.079 |
经过主成分分析后所有变量的系数均通过t检验,而且自变量之间几乎不存在共线性,模型校正R2值也提高到了0.737,表明以上主成分可用于进一步构建流感空间分布的局部模型。
3.2 基于GWR的空间分布模型使用相同的数据集,基于地理加权回归构建流感空间分布模型,结果见表 3,表中用四分位数来表示各参数的变化情况。
| 分位 | 截距 | PC1 | PC2 | PC3 |
| 最小值 | 402.88 | 71.67 | -173.83 | -139.96 |
| 下四分位 | 547.85 | 360.64 | 52.85 | 126.20 |
| 中位数 | 694.92 | 531.44 | 216.95 | 278.22 |
| 上四分位 | 754.08 | 705.12 | 357.01 | 457.13 |
| 最大值 | 1 135.97 | 933.56 | 1 058.04 | 883.03 |
| 调整R2 | 0.915 | |||
| AIC | 2 195.12 | |||
| RSS(108) | 1.321 |
GWR模型的拟合度为0.915,与OLS模型相比有大幅度的提高。在不同空间位置上,GWR模型的参数估计值存在较大变化,这一变化表明,各解释变量对发病数的影响作用大小甚至正负都不一致。过往的研究也表明,网络搜索行为存在一定的空间差异性特征,不同地区不同属性的关键词与真实病例数有不同的相关性[15],而OLS模型未能考虑这种变化特征。
3.3 基于GTWR的空间分布模型进一步运用GTWR模型对训练集中的数据进行分析并构建流感空间分布模型,模型参数估计值及性能指标见表 4。
| 分位 | 截距 | PC1 | PC2 | PC3 |
| 最小值 | -190.86 | -724.85 | -940.00 | -226.68 |
| 下四分位 | 515.41 | 399.34 | 96.12 | 168.49 |
| 中位数 | 723.03 | 522.17 | 290.29 | 314.13 |
| 上四分位 | 925.64 | 731.01 | 495.04 | 472.17 |
| 最大值 | 1 507.78 | 1 306.51 | 1 107.80 | 1 190.98 |
| 调整R2 | 0.959 | |||
| AIC | 2 115.10 | |||
| RSS(108) | 0.631 |
结果表明,模型可解释实际发病数变化的百分比进一步提高到了95.9%。在不同的时间和空间上,GTWR模型参数估计值的变化程度大于GWR模型。AIC值是模型性能的另一种度量,用于比较不同的回归模型,一般情况下,简单的全局模型具有更好的可操作性和解释性,而复杂的局部模型有更好的拟合度,若拟合度差异不大,应尽量选择简单的模型。AIC值考虑了模型复杂度,具有越小AIC值的模型性能越好,不同模型之间的AIC值相差超过3,表明模型性能差异显著[16]。可以看出,AIC值从OLS的2 313.12降低到GWR的2 195.12及GTWR的2 115.10,降低幅度远远大于3,说明模型之间存在显著差别。残差是模型无法解释的部分,从OLS模型到GTWR模型,残差平方和(residual squares,RSS)逐渐降低。
虽然GTWR模型相对GWR模型的拟合度有所提升,但GWR模型相对OLS模型的提升更大,AIC值的变化也呈现出这样的特征,可能的原因是试验数据的时间跨度相对较小,而空间跨度较大,导致时间非平稳性的影响要小于空间非平稳性。综上可见,由于回归因素中存在时空非平稳性,而GTWR模型同时考虑了时间和空间非平稳性的影响,因此能更好地模拟流感发病的空间分布。
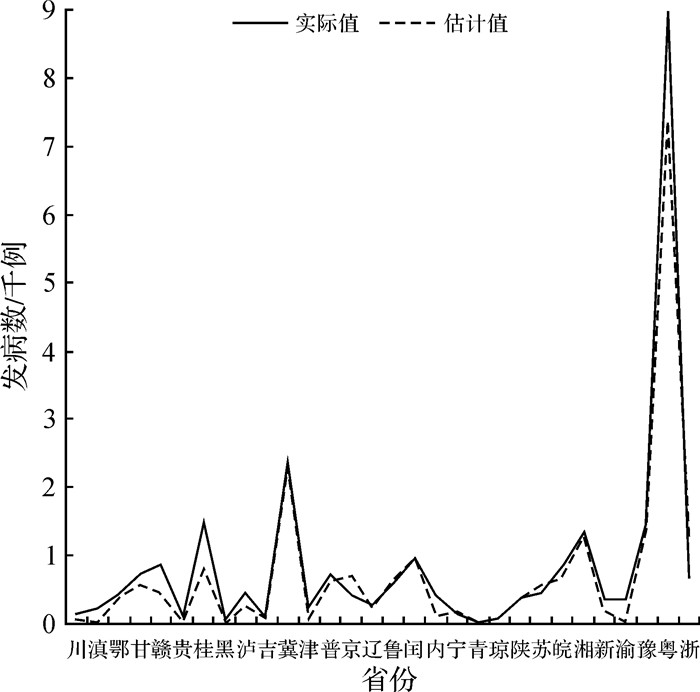
4 GTWR模型的验证使用回归分析方法对现象建模后可用于估算其他时间的数值[17]。在使用训练集建立模型,并比较模型拟合效果的基础上,选用GTWR模型对流感发病数进行估算,把验证集的解释变量即3个主成分代入回归计算所得的模型中,得出2014年3月各省发病数的估计值。将未参与模型参数估计的3月各省实际发病数据作为模拟目标值用于与估算值进行对比,如图 2所示。
|
| 图 2 各省发病数的估计值与实际值比较 |
从图 2可以看出,发病数的估计值与真实值基本吻合,模型能准确识别流感高发地区和低发地区,尤其在高发地区模拟效果更佳,但低发地区的拟合情况较差,可能是由于流感疫情严重的地区产生的搜索信息更为全面,使得模型对高值的估算较为准确。为了进一步验证模型的预测能力,可通过对估计值与实际值进行空间相关性分析来比较两者的接近程度[18]。结果表明,估计值与实际值相关系数达到0.956,在0.01水平上显著相关,说明结合GTWR模型和搜索引擎数据可以较为准确地模拟流感发病的空间分布。
5 结语本文依据关键词的百度指数与流感发病数之间的相关性进行关键词选取,用于构造回归模型;针对回归分析中经常存在的多重共线性问题,使用主成分分析法消除变量共线性;为了表达模型的时空非平稳性,构建时空地理加权回归流感空间分布模型。研究结果表明,流感发病数与相关关键词百度指数之间存在明显的时空非平稳性,与全局回归模型相比,变系数的局部回归模型能显著提高模型拟合程度,其中时空地理加权回归模型效果最佳,结合搜索引擎数据能准确识别流感高发地区,实时监测流感发病空间分布情况。该方法较常规监测方法具有更高的时效性,而且数据获取和计算成本低廉,可用于早期预警,成为传统疾病监测方法的有效补充。
| [1] | 胡雪芸, 何宗宜, 苗静. 疾病数据的时空聚集分析及可视化[J]. 测绘通报, 2015(11): 106–111. |
| [2] | 单杰, 秦昆, 黄长青, 等. 众源地理数据处理与分析方法探讨[J]. 武汉大学学报(信息科学版), 2014, 39(4): 390–396. |
| [3] | 艾廷华. 大数据驱动下的地图学发展[J]. 测绘地理信息, 2016, 41(2): 1–7. |
| [4] | 鲁力, 邹远强, 彭友松, 等. 百度指数和微指数在中国流感监测中的比较分析[J]. 计算机应用研究, 2016(2): 392–395. |
| [5] | 李秀婷, 刘凡, 董纪昌, 等. 基于互联网搜索数据的中国流感监测[J]. 系统工程理论与实践, 2013, 33(12): 3028–3034. DOI:10.12011/1000-6788(2013)12-3028 |
| [6] | GINSBERG J, MOHEBBI M H, PATEL R S, et al. Detecting Influenza Epidemics Using Search Engine Query Data[J]. Nature, 2008, 457(7232): 1012–1014. |
| [7] | 王若佳, 李培. 基于互联网搜索数据的流感监测模型比较与优化[J]. 图书情报工作, 2016(18): 122–132. |
| [8] | 焦利民, 许刚, 赵素丽, 等. 基于LUR的武汉市PM2.5浓度空间分布模拟[J]. .武汉大学学报(信息科学版), 2015, 40(8): 1088–1094. |
| [9] | 赵阳阳, 刘纪平, 徐胜华, 等. 一种基于半监督学习的地理加权回归方法[J]. 测绘学报, 2017, 46(1): 123–129. DOI:10.11947/j.AGCS.2017.20150470 |
| [10] | 张金牡, 刘彪, 吴波, 等. 应用改进的时空地理加权模型分析城市住宅价格变化[J]. 东华理工大学学报(自然科学版), 2010, 33(1): 53–59. |
| [11] | HUANG B, WU B, BARRY M. Geographically and Temporally Weighted Regression for Modeling Spatio-temporal Variation in House Prices[J]. International Journal of Geographical Information Science, 2010, 24(3): 383–401. DOI:10.1080/13658810802672469 |
| [12] | 董晓春, 李琳, 徐文体, 等. 特定关键词及百度指数与流感病毒活动相关性分析[J]. 中国公共卫生, 2016(11): 1543–1546. DOI:10.11847/zgggws2016-32-11-25 |
| [13] | YUAN Q, NSOESUE E O, LV B, et al. Monitoring Influenza Epidemics in China with Search Query from Baidu[J]. Plos One, 2013, 8(5): e64323. DOI:10.1371/journal.pone.0064323 |
| [14] | 王旭, 林征, 张志, 等. 基于GWR模型的北极滨海平原融冻湖表面温度空间分布模拟[J]. 武汉大学学报(信息科学版), 2016, 41(7): 918–924. |
| [15] | 黄达沧. 基于搜索引擎数据的手足口病监测[D]. 长春: 东北师范大学, 2015: 27-32. http://cdmd.cnki.com.cn/Article/CDMD-10200-1015418218.htm |
| [16] | 覃文忠, 王建梅, 刘妙龙. 混合地理加权回归模型算法研究[J]. 武汉大学学报(信息科学版), 2007, 32(2): 115–119. |
| [17] | ZHANG H, GUO L, CHEN J, et al. Modeling of Spatial Distributions of Farmland Density and Its Temporal Change Using Geographically Weighted Regression Model[J]. Chinese Geographical Science, 24(2): 191-204. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=zdkx201402005&dbname=CJFD&dbcode=CJFQ |
| [18] | LAMPOS V, CRISTIANINI N. Tracking the Flu Pandemic by Monitoring the Social Web[C]//2010 Second International Workshop on Cognitive Information Processing(CIP). Elba: IEEE, 2010: 411-416. |


