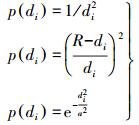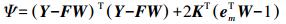地壳垂直运动是地壳运动的一个重要分量,由于空间大地测量技术测定的高程分量精度低于水平分量,因此利用重复高精度水准测量仍然是目前研究地壳垂直运动的主要方法。但由于水准重合点是离散的,且水准网内部没有数据,因此动态平差得到的垂直运动速率在时间域和空间域都是不连续的,实际上地壳垂直运动是一种连续的形态变化。为了实现在时空域内客观准确地描述形变分布特征,往往需要基于离散的测点数据构建合适的数学模型拟合(最佳逼近)整个地区的地壳垂直形变速率面[1]。
在我国,从20世纪80年代末期开始,黄立人、赵承坤、杨国华和陶本藻等研究了多面函数拟合法在地壳垂直运动中的应用,几位学者针对多面函数拟合中核函数的选择、平滑因子的选择及核函数中心点的选择作了细致的研究,并提出了一系列独特的见解[2-6]。刘经南等[7]研究了多面函数拟合法在建立我国地壳平面运动速度场模型中的应用。王文利等[8]利用多面函数拟合了我国陆地垂直运动速率图。刘同文等[9]应用多面函数模型对西秦岭地区的垂直形变速率作了研究和探讨。秦姗兰等[10]利用水准资料研究了西秦岭地区的垂直形变,应用多面函数对区域整体形变特征进行拟合。
综上所述,研究地壳垂直运动中,多面函数法是一种非常传统并得到广泛应用的方法,而其他方法应用并不多。本文应用多面函数和移动法综合拟合模型,并以首都圈和晋冀蒙两个地区的垂直运动为例,与其他几种模型作对比研究。
1 模型方法数学原理 1.1 多面函数模型多面函数模型是由美国Hardy教授于1977年提出的,并建议用于地壳垂直形变分析。该方法的基本思想为:任何数学表面和任何不规则的圆滑表面,总可以用一系列有规则的数学表面的和以任意精度逼近[9]。根据这一思想,假设地球表面上有一点(x, y),其垂直速率值ξ(x, y)可以用下式来表示
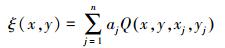 (1)
(1) 式中,aj为待定系数;Q(x, y, xj, yj)是多面函数的核函数。核函数有多种类型,常用的有距离型核函数和锥面函数,其中距离型核函数表达式为
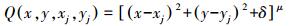 (2)
(2) 式中,δ为平滑因子,通常可取一小正数或0;μ一般取1/2、-1/2、3/2。当μ=1/2时,核函数称为正双曲面函数;当μ=-1/2时,核函数称为倒双曲面函数;当μ=3/2时,核函数称为三次曲面函数。
锥面函数表达式为
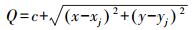 (3)
(3) 式中,c为待定参数。
设有m个已知水准点(xi, yi),选取其中n(n≤m)个点作为核函数的中心点(xj, yj),令Qij=Q(xi, yi, xj, yj),则各数据点应满足
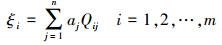 (4)
(4) 由此可列出误差方程
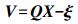 (5)
(5) 根据最小二乘原理可求得待定系数X,即
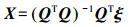 (6)
(6) 待定系数求出后,根据式(4)可计算测区各未知点的垂直形变速率值。
需要注意的是,应用多面函数拟合垂直形变速率时,要根据测区大小和地形情况确定合适的核函数、平滑因子和中心点个数。
1.2 移动曲面模型移动曲面模型的基本原理是以每一个待定点为中心,选取待定点周围适量的已知点,拟合出一个多项式曲面,进而内插出待定点上的函数值,是一种特殊的局部函数逼近法。
为了选取邻近的数据点,以待定点P(xp, yp)为圆心,以R为半径作圆,凡落在圆内的数据点即被选用。应用时要根据实际情况选择合适的半径R。
定权时要根据已知点与待定点间的距离进行定权,常采用的权有以下几种形式
式中,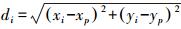
在进行拟合前,可先将参与拟合的各点坐标进行中心化处理,即将各点坐标减去待定点P的坐标,这样转换后就变成以P为原点的坐标
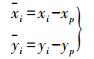 (7)
(7) 用这些中心化后的坐标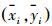
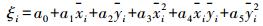 (8)
(8) 最后求待定点P的垂直形变速率时,直接代入坐标(0, 0)即可,从而在很大程度上方便了计算,而且有利于改善方程的数值稳定性和提高解算精度[11]。
1.3 多面函数和移动法加权综合模型该方法是基于综合预报理论提出的,它并不是一种全新的方法,而是首先采用多面函数和移动法进行单独拟合,然后对其拟合值进行加权综合而得到最终拟合值[12]。用数学模型可表示为
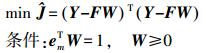 (9)
(9) 式中,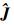
文献[12]中并没有给出该模型解的具体解法和表达式,本文给出W解的具体解法如下:
先构造拉格朗日极值函数
令
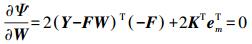 (10)
(10) 由式(10)等号两边同乘以W结合条件emTW=1可得
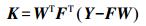 (11)
(11) 另外,由式(10)可得
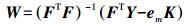 (12)
(12) 由式(11)和式(12)可采用迭代法解得W
(1) 令W0=[0.5 0.5]T(初值选为等权,即由n个单一模型加权综合,权值为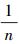
(2) 将W0代入式(11)计算K。
(3) 将K代入式(12)计算W。
(4) 判断|W-W0| < 10-6, 若是,退出循环;若否,令W0=W继续重复步骤(2)—(4)。
经过以上迭代过程即可解得W为W*,则相应综合模型拟合结果为
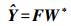 (13)
(13) 多面函数法对整体性变化的拟合效果较好,但需要确定合适的模型参数,如果选取不当,容易出现拟合结果波动较大的现象,对局部变化拟合效果较差;而移动拟合法是以待定点为中心,以一定距离为半径,用一个多项式曲面拟合待定点函数值的局部拟合法,具有较好的灵活性[13]。为此,可以结合两者优点,采用先进行多面函数拟合,再对残差进行移动法拟合的综合模型拟合垂直形变速率。这很类似于组合法确定似大地水准面中的“移去—恢复”法,具体步骤如下:
(1) 在测区内选取m个已知速率ξ的水准点作为多面函数的拟合点,并以此求解出各拟合点的速率拟合值ξN和待定点的速率拟合值ξ′N。
(2) 求出m个拟合点的速率拟合残差v
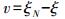 (14)
(14) (3) 将各拟合点的v值作为已知值运用移动拟合法进行第二次拟合,求出待定点的拟合残差v′,将步骤(1)拟合得到的速率值ξ′N与v′相减,即得待定点的速率值ξ′
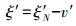 (15)
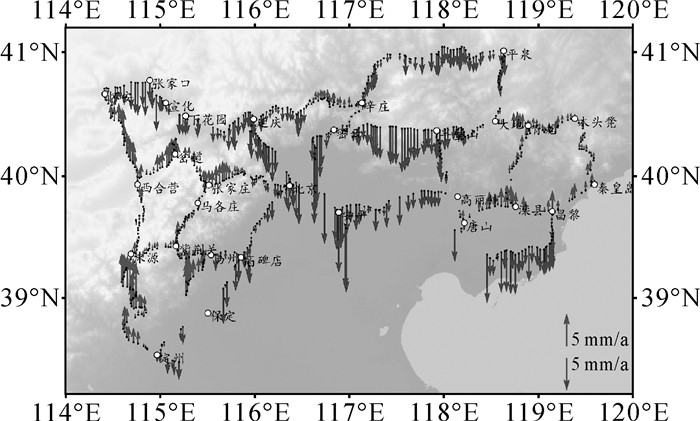
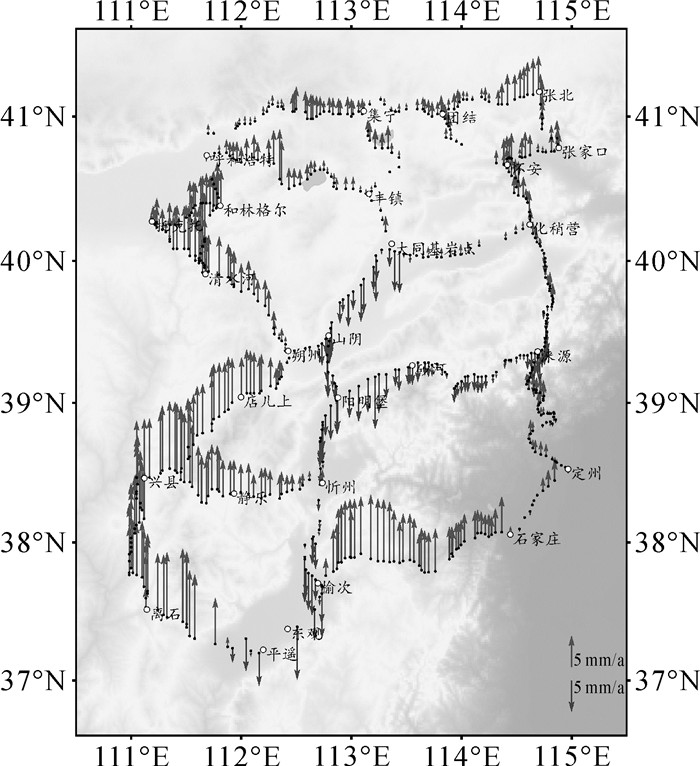
(15) 本文选用首都圈地区2001年和2005年,以及晋冀蒙地区2002年和2006年各两期水准数据进行研究,并对两个地区的数据采用自由网平差法进行动态平差,计算垂直运动速率。两段动态平差的单位权中误差分别为1.03和1.15 mm/a,说明这两个区域的数据整体实测精度比较好。剔除平差后速率中个别量值过大的突变点,首都圈地区共选用719个具有平差后速率的数据点(如图 1所示),晋冀蒙地区共有627个具有平差后速率的数据点(如图 2所示)。由于对一个区域垂直形变场的拟合研究,主要为了得到未测点的垂直形变速率(即水准环内部区域的垂直形变速率),因此为了更充分地得出结论,采用以下4种方案分别进行拟合计算:
|
| 图 1 首都圈地区垂直形变速率(相对于北京) |
|
| 图 2 晋冀蒙地区垂直形变速率(相对于大同) |
方案1:均匀选取首都圈地区143个点作为外部检核点(约占总点数的1/5),其余576个点作为拟合点参与函数模型的参数拟合(针对路线上数据)。
方案2:选取首都圈地区5条水准环内部路线全部点作为外部检核点(共80个点),其余639个点作为拟合点参与函数模型的参数拟合(针对环内部数据)。
方案3:均匀选取晋冀蒙地区125个点作为外部检核点(约占总点数的1/5),其余502个点作为拟合点参与函数模型的参数拟合(针对路线上数据)。
方案4:选取晋冀蒙地区5条水准环内部路线全部点作为外部检核点(共60个点),其余567个点作为拟合点参与函数模型的参数拟合(针对环内部数据)。
本文采用外符合精度及检核点速率拟合值与实际观测值之差(残差)的绝对值大于2 mm/a的点的个数来衡量拟合的精度。外符合精度σ的表达式为
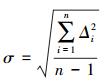 (16)
(16) 式中,Δi表示检核点速率拟合值与实际观测值之差;n为检核点个数,并称Δ|i|>2 mm/a的点为病态点。
2.2 各种模型拟合结果比较对首都圈地区的拟合计算有方案1和方案2,各种模型拟合结果见表 1。
| 模型方法 | 方案1 | 方案2 | |||
| 外符合精度/(mm/a) | 病态点个数/个 | 外符合精度/(mm/a) | 病态点个数/个 | ||
| 多面函数 | 0.825 | 6 | 1.365 8 | 10 | |
| 移动曲面 | 0.883 3 | 7 | 1.346 3 | 13 | |
| 多面函数和移动法加权综合模型 | 0.823 5 | 7 | 1.338 8 | 11 | |
| 多面函数和移动法综合拟合模型 | 0.823 4 | 6 | 1.336 6 | 10 | |
表 1中各种模型的拟合结果都是在多次试算调整参数后得到的最优结果。方案1中多面函数的核函数选择锥面函数,其中参数c取100;移动曲面中移动窗口半径为0.8,权函数选择p(di)=1/di2;多面函数和移动法综合模型中移动法拟合残差时移动窗口半径选择2,权函数选择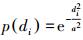
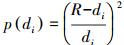
为了直观地看出各种模型的拟合效果,给出不同模型在方案1和方案2中拟合检核点速率残差情况,如图 3和图 4所示。
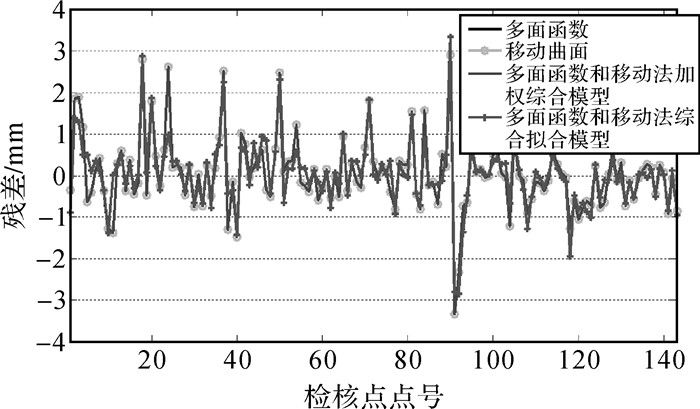
|
| 图 3 方案1不同模型检核点拟合残差 |
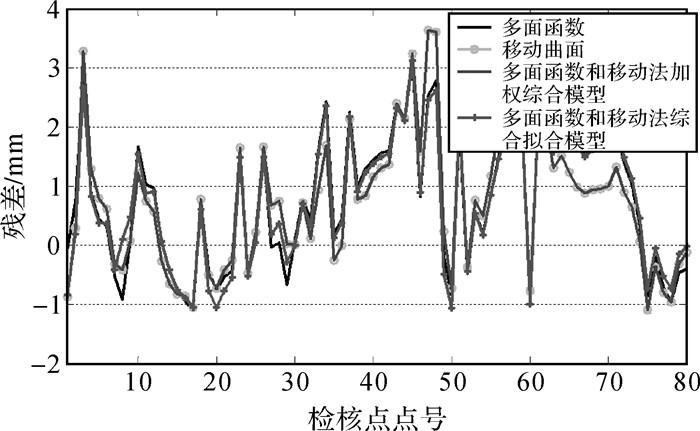
|
| 图 4 方案2不同模型检核点拟合残差 |
对晋冀蒙地区的拟合计算有方案3和方案4,各种模型拟合结果见表 2。
| 模型方法 | 方案3 | 方案4 | |||
| 外符合精度/(mm/a) | 病态点个数/个 | 外符合精度/(mm/a) | 病态点个数/个 | ||
| 多面函数 | 1.105 3 | 10 | 1.177 7 | 5 | |
| 移动曲面 | 1.258 3 | 9 | 1.193 2 | 9 | |
| 多面函数和移动法加权综合模型 | 1.085 2 | 9 | 1.139 2 | 9 | |
| 多面函数和移动法综合拟合模型 | 1.079 | 8 | 1.132 2 | 3 | |
表 2中各种模型的拟合结果同样是在多次试算调整参数后得到的最优结果。方案3中多面函数的核函数选择锥面函数,其中参数c取100;移动曲面中移动窗口半径为0.9,权函数选择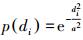
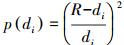
为了直观地看出各种模型的拟合效果,给出不同模型在方案3和方案4中拟合检核点速率残差情况,如图 5和图 6所示。
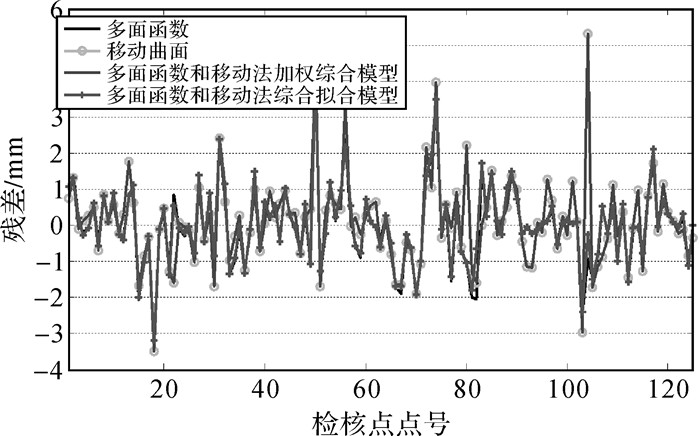
|
| 图 5 方案3不同模型检核点拟合残差 |
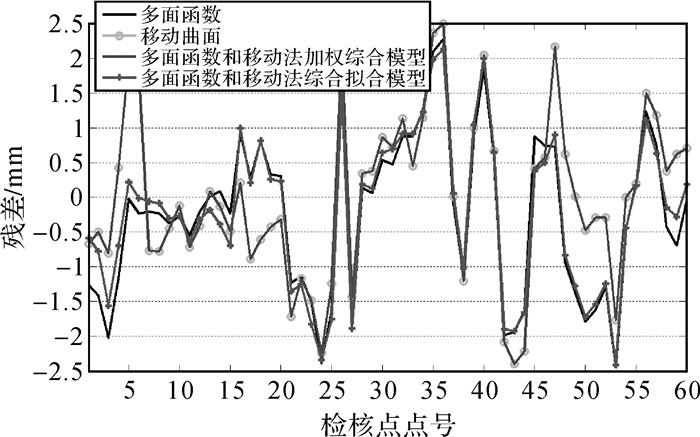
|
| 图 6 方案4不同模型检核点拟合残差 |
(1) 从表 1和表 2中可以发现,4种模型中两种综合模型的拟合精度优于两种单一模型,但是特性不同。多面函数和移动法加权综合模型虽然精度上优于多面函数模型,但是病态点个数并不具有优势,这是因为加权综合会使得单一模型的各种误差传递到最终结果中。而多面函数和移动法综合拟合模型不管在精度上还是病态点个数上均优于多面函数模型。
(2) 多面函数和移动法综合拟合模型在两个地区4种不同情况下都是4种模型中拟合精度最高的,病态点数也是最少的,并且从图 4-图 7可以看出多面函数和移动法综合拟合模型的拟合残差是最稳定的。
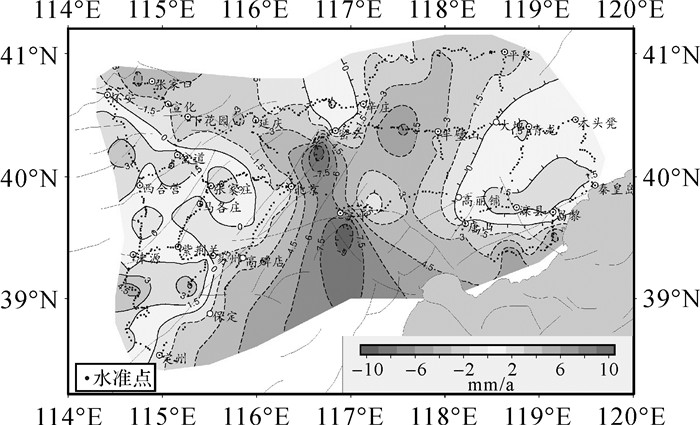
|
| 图 7 首都圈地区垂直形变速率等值线 |
利用多面函数和移动法综合拟合模型对首都圈和晋冀蒙地区的垂直形变速率进行拟合,并进行格网化处理,格网间距设为1′×1′,得到两个地区的垂直形变速率等值线图,如图 7和图 8所示。
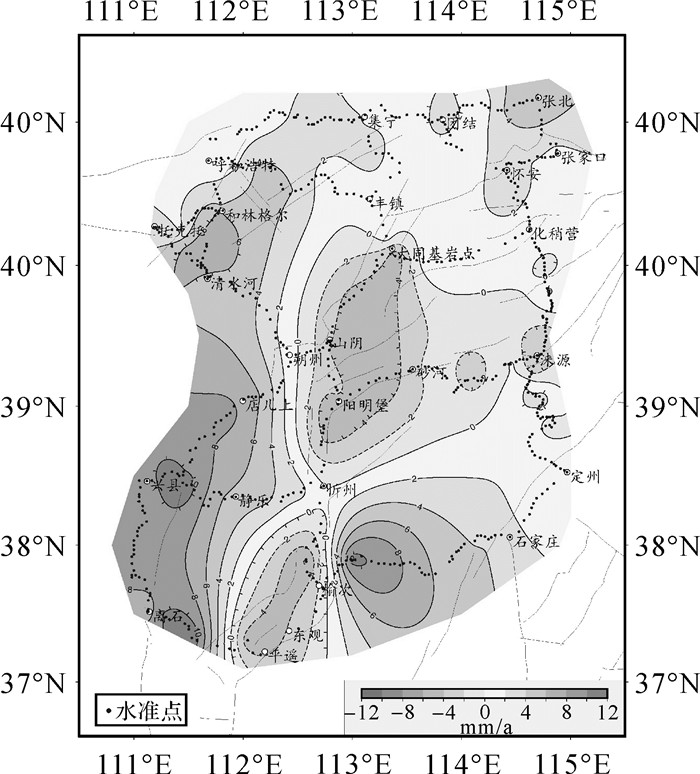
|
| 图 8 晋冀蒙地区垂直形变速率等值线 |
从图 7和图 8可以发现首都圈和晋冀蒙两个地区用多面函数和移动法综合拟合模型得到的垂直形变速率等值线图与图 1和图 2的速率图反映的升降情况吻合度较好,说明该模型可以用于这两个地区的垂直形变场拟合。
3 结论(1) 两种综合模型的拟合精度优于两种单一模型,但多面函数和移动法加权综合模型会使得单一模型的各种误差传递到最终结果中,从而导致病态点个数较多。而多面函数和移动法综合拟合模型不管在精度上还是病态点个数上都优于多面函数模型。
(2) 多面函数和移动法综合拟合模型在首都圈和晋冀蒙两个地区4种情况下都是拟合精度最高、病态点数最少、拟合残差最稳定的,并且应用该模型拟合这两个地区的垂直形变场得到的等值线图与速率图吻合度较好,具有一定的实际应用价值。
| [1] | 郝明. 基于精密水准数据的青藏高原东缘现今地壳垂直运动与典型地震同震及震后垂直形变研究[D]. 北京: 中国地震局地质研究所, 2012. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=gjzt201307008&dbname=CJFD&dbcode=CJFQ |
| [2] | 黄立人, 杨国华, 刘天奎. 用速率面拟合法研究华北部分地区的现今地壳垂直运动[J]. 地壳形变与地震, 1989, 9(3): 26–34. |
| [3] | 赵承坤, 黄立人. 速率面拟合法中核函数中心点的选择[J]. 地壳形变与地震, 1991, 11(2): 48–54. |
| [4] | 陶本藻, 王新洲, 于正林, 等. 用于垂直形变模型的多面函数拟合法的试验研究[J]. 地壳形变与地震, 1992, 12(1): 1–12. |
| [5] | 杨国华, 黄立人. 速率面拟合法中多面函数几个特性的初步数值研究[J]. 地壳形变与地震, 1990, 10(4): 70–82. |
| [6] | 黄立人, 陶本藻, 赵承坤. 多面函数拟合在地壳垂直运动研究中的应用[J]. 测绘学报, 1993, 22(1): 25–32. |
| [7] | 刘经南, 施闯, 姚宜斌, 等. 多面函数拟合法及其在建立中国地壳平面运动速度场模型中的应用研究[J]. 武汉大学学报(信息科学版), 2001, 26(6): 500–503. |
| [8] | 王文利, 陈士银, 董鸿闻, 等. 利用多面函数拟合中国陆地垂直运动速率图[J]. 测绘通报, 2002(8): 6–8. |
| [9] | 刘同文, 杨志强, 王慧敏. 西秦岭地区垂直形变的分析研究[J]. 测绘科学, 2014, 39(4): 61–63. |
| [10] | 秦姗兰, 王庆良, 季灵运, 等. 利用水准资料研究西秦岭地区的垂直形变[J]. 大地测量与地球动力学, 2012, 32(2): 16–19. |
| [11] | 徐绍铨, 张华海, 杨志强, 等. GPS测量原理及应用[M]. 武汉: 武汉大学出版社, 2008. |
| [12] | 赵超英, 张勤. 地壳垂直形变场的综合逼近模型[J]. 大地测量与地球动力学, 2003, 23(2): 42–44. |
| [13] | 田晓, 郑洪艳, 许明元, 等. 一种改进的适用于不同地形的GPS高程拟合模型[J]. 测绘通报, 2017(1): 35–38. |