2. 中南大学地球科学与信息物理学院, 湖南 长沙 410012
2. School of Geosciences and Info-physics, Zhongnan University, Changsha 410012, China
2013年以来,每年仅中国产生的数据总量就达到ZB级,相当于2009年全球的数据总量,而其中具有空间属性的数据大约有80%[1]。地籍数据是一种典型性、复杂性的空间数据,其在数据海量性环境下的质量控制是亟待解决的问题,而地籍数据拓扑的一致性是其核心问题[2-3]。虽然近年计算机的计算能力迅速提高,尤其是多核计算机和并行计算机开始普及,但地籍数据本身的空间复杂性,使得传统串行环境下的空间拓扑检查方法难以充分利用这些先进的计算资源,已远不能满足实际应用中地籍数据拓扑一致性检查效率的需求[4]。现有的并行技术、分布式技术、云技术正在与GIS理论进行着深度融合[5],在栅格方面进行的数据并行算法研究[5-6]较多,但在矢量方面关于并行拓扑质量检查的研究较少[7-9]。
本文在分析拓扑关系计算特点的基础上,结合四叉树和R树的多级多重并行空间索引(Q&R索引),解决了矢量地理对象数据的快速定位(数据过滤)和空间分割问题;同时提出一种基于Q&R索引实现拓扑计算过程中任务调度的方法,从数据层实现空间拓扑关系计算的并行化。
1 拓扑关系原理与高性能计算模式 1.1 拓扑关系基本原理拓扑关系是GIS的重要特征,表达空间目标之间的在空间上相邻程度的一种定性关系。现有空间拓扑关系的描述模型主要有3种[9]:基于点集理论的描述模型(4-交模型与9-交模型)、基于RCC理论的描述模型、基于Voronoi图的9-交模型。相较于RCC理论描述模型和Voronoi图,9-交模型适用几何对象广泛且有相对较高的计算效率,更加适用于研发拓扑关系计算的高性能算法(见表 1)。
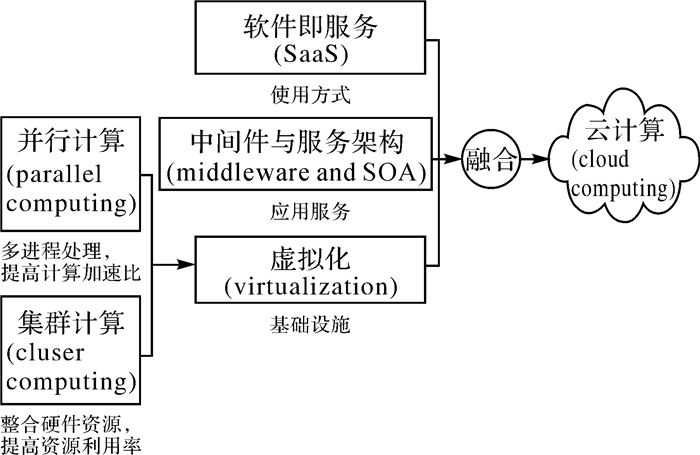
现有空间高性能计算环境主要分为并行计算、分布式计算、集群计算与云计算等,其共同点在于通过并行化算法充分利用更多的计算资源,以实现空间数据和空间分析的高效计算,而区别在于其计算模式不同[9-12]。不同于其他高性能计算,云计算是未来的发展趋势,其特征在于空间计算资源的弹性化供给[11-13]。云计算通过虚拟化技术和资源管理技术为用户提供多种虚拟的高性能计算环境(如图 1所示),如并行计算环境、分布式计算环境等。
|
| 图 1 云计算平台 |
据上所述,本文主要研究拓扑关系的并行化方法,以期在云平台下虚拟并行环境或集群环境下高效运行。本文采用单程序多数据(single program multiple data,SPMD)[14]模式设计拓扑计算并行算法,基本思路为:通过空间数据集划分方法,将空间数据分配至不同进程;在空间索引支持下,各进程对不同的空间数据集进行协同并行计算。
2 拓扑关系并行计算策略 2.1 拓扑关系检查计算特点分析拓扑关系的基础算法属于计算几何方法的一部分,其粒度最小的算子可归纳为节点间关系计算、点与线间关系计算,而拓扑关系检查计算是在某些约束条件下进行点与点之间或点组与点组之间的计算。矢量数据基本要素有点(Pi)、线(Li)、面(Poi),而以上数据都是由点要素构成,即Poi={L1, L2, …, Lm},Li={P1, P2, …, Pn}。点是矢量数据中最简单、最结构化的要素,假定点每次参与计算的计算量为Cp,则矢量目标之间的关系计算,如线、线求交,属于“乘积”型几何计算,其计算量Cp为
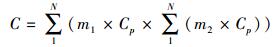 (1)
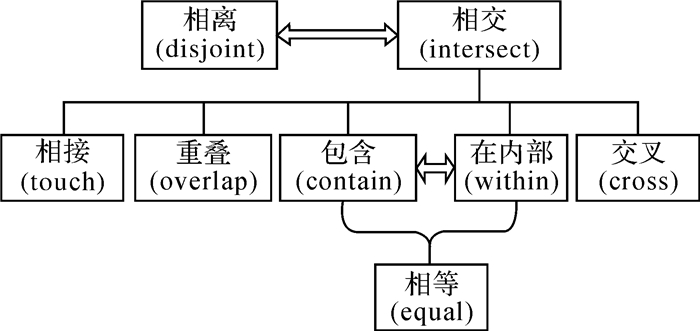
(1) 根据矢量目标之间拓扑关系的层次化计算关系(如图 2所示),分析拓扑关系计算的层次关系,可知其特点为:①对于某一矢量目标,需判断其与矢量目标集中的其他所有对象是否相交;②只进一步计算与其相交的矢量目标间的精细拓扑关系。
|
| 图 2 空间拓扑关系之间的联系与计算层次 |
分析特点①可知:矢量目标之间一般先通过MBR(minimum bounding rectangle)的相交计算,过滤掉大部分相离的矢量目标集;若采用复杂度最高的MBR直接过滤法,过滤耗时将急剧增加,严重制约着拓扑计算的效率。因此,要实现高效拓扑关系并行计算,首先需要研究一种高效过滤非相交的矢量目标算法。
分析特点②可知:拓扑关系计算中的矢量目标可分解为约束条件下的点点拓扑计算集或点线拓扑计算集,若将计算集分治计算会破坏矢量目标数据的完整性。因此,需要从数据集上设计一种拓扑关系的并行化方法,既顾及矢量目标数据的完整性,又提升拓扑关系并行计算的效率。
由上述分析可知:通过功能划分实现拓扑关系的并行化会破坏矢量目标的数据完整性,而通过数据划分实现拓扑计算并行化具有较高的可行性。数据划分的约束条件有:①将空间索引与数据划分相融合,提高相离矢量目标集(命中相交矢量目标集)的过滤效率,从数据划分方法上实现拓扑关系计算量划分均衡(任务均衡);②任务均衡通过计算量模型“乘积”相等实现,即与任一矢量目标集A有相交关系的各节点中矢量目标集合Sn(1 < n < p, p为节点数),其中f(A)为A的点数,f(Sn)为Sn的边数,采用式(1)计算,则f(A)×f(S1)≈f(A)×f(S2)≈…≈f(A)×f(Sn)都近似相等。
2.3 数据划分方案根据以上分析,对于计算量属于“乘积”方式的空间拓扑计算,在数据划分后仍保持各节点的计算量C近似相等,则各节点中要素集的点总数需近似相等,且需从各层数据的空间分布及参与计算的概率考虑,各层检索与矢量目标集A可发生相交计算的要素集点数需要近似相等。因此,需要结合基于四叉树(Q树)数据初步划分和顾及“乘积”计算量的再次划分(再次划分后建立R树),即在划分数据的过程中,不仅从数据层实现了负载(任务)均衡,并且构建的Q&R并行索引也极大提高了数据筛选的效率,特别是在海量数据的环境下更能发挥出Q&R并行索引优势,提升并行拓扑计算的效率。
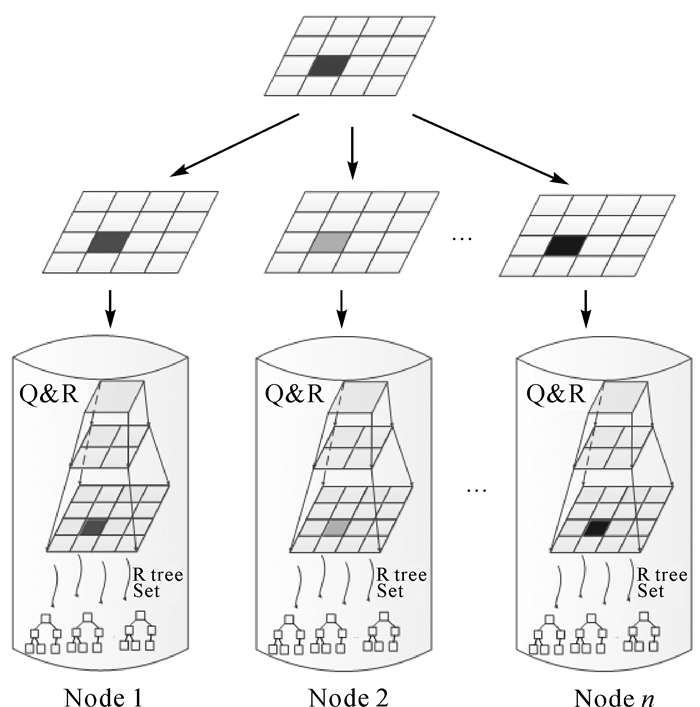
首先,通过Q树叶子节点对矢量目标集进行初始范围划分,将空间数据集V分割为数据块集S{dS1, dS2, …, dSm}, Q树各叶子节点包含对应的数据块dSn;其次,将各叶子节点中矢量目标数据块dSn进一步划分为dS{dSnc1, dSnc2, …, dSncp},分配至各计算节点(将Q树各叶子节点切片为p个叶子节点,即将Q树切为p个深度相同的Q树),使各计算节点位置相同的Q树叶子节点的Cp近似相等,并对dS集合建立R树索引,进一步提升数据筛选的效率(如图 3所示)。
|
| 图 3 数据划分过程 |
拓扑关系计算分为两种情况:①空间数据集A与空间数据集B的空间拓扑计算,筛选出符合拓扑约束条件c(c为相离、相接、叠加、包含或穿越)的空间数据C;②空间数据集A中各空间数据之间的拓扑关系,可理解为空间数据集A与空间数据集A的空间拓扑计算。因此,两种情况可采用相同的并行方式。具体步骤如下(设并行程序运行的进程数为P):
(1) 根据本文的数据划分方法对空间数据集A进行划分,并建立Q & R并行索引(包含P个Q&R索引)。
(2) 根据本文的四叉树划分(Q树深度为m)方法对空间数据集B进行划分,划分后数据块为S1, S2, …, Sm×m。
(3) 各进程读取空间数据块Sn(1 < n≤m2),且各进程不能读取同一空间数据集(提升读取效率,不占用集群过多的计算资源,且在共享模式下可减少通信消耗),那么各进程(进程号为p,0≤p < P)读取的顺序为:若p=0,则为S(p+1)→Sm×m;若p>0, 则为S(p+1)→Sm×m→S(p)。
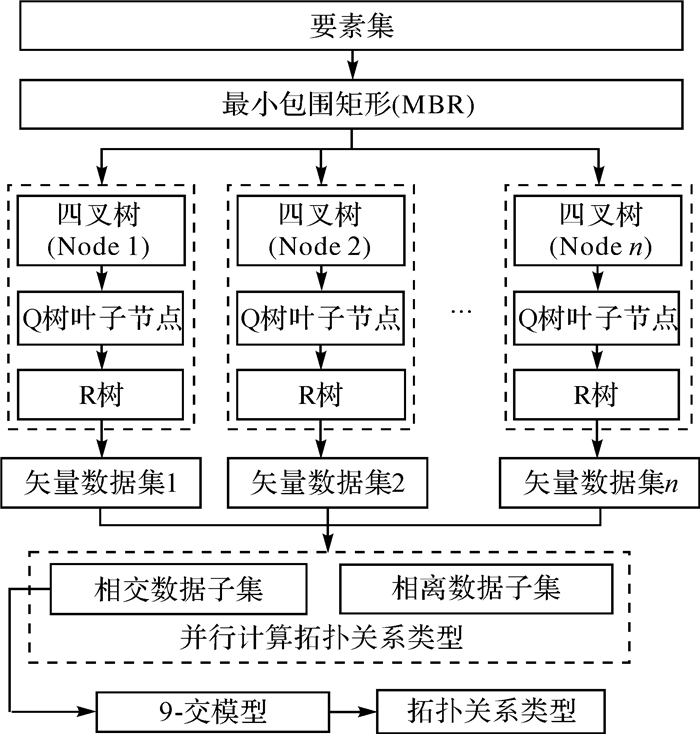
(4) 各进程读取数据块Sn中空间目标oi的MBR,在该节点对应的Q&R索引中检索与其进行拓扑计算的数据集di,oi与di采用V-9I模型进行拓扑计算(如图 4所示)。
|
| 图 4 拓扑关系并行计算流程 |
(5) 重复步骤(4)直至数据块Sn中所有空间目标都计算完毕。
(6) 重复步骤(3)-(5)直至各进程中所有空间数据块(S1, S2, …, Sm×m)都参与计算各节点Q&R索引对应的空间数据集完毕。
(7) 收集各进程拓扑计算中符合约束条件的结果。
3 应用试验分析本文基于消息传递接口模式的并行框架,采用C++语言实现跨平台的并行算法开发,实现并行算法在不同的硬件环境下(如单机、集群和云环境)运行。
3.1 应用环境空间拓扑并行计算中间件部署在云平台下的虚拟集群中,为实际应用提供服务。该环境由5个虚拟计算节点及1个虚拟存储节点(4 TB)构成,集群中各节点的操作系统是Redhat 5.04(64位),消息传递采用OpenMPI并行库,节点间采用高速交换机进行通信,见表 2。
本试验有两组应用数据:①矢量目标集1为国内某地区的5.6万块宗地;②矢量目标集2为某地区70万块宗地,其中第1组试验数据用于正确性验证,参照对象ArcGIS;第2组数据相比第1组数据提升了一个数量级,在单节点环境下已超出ArcGIS的计算能力,用于验证本文提出拓扑关系计算方法的并行性能。
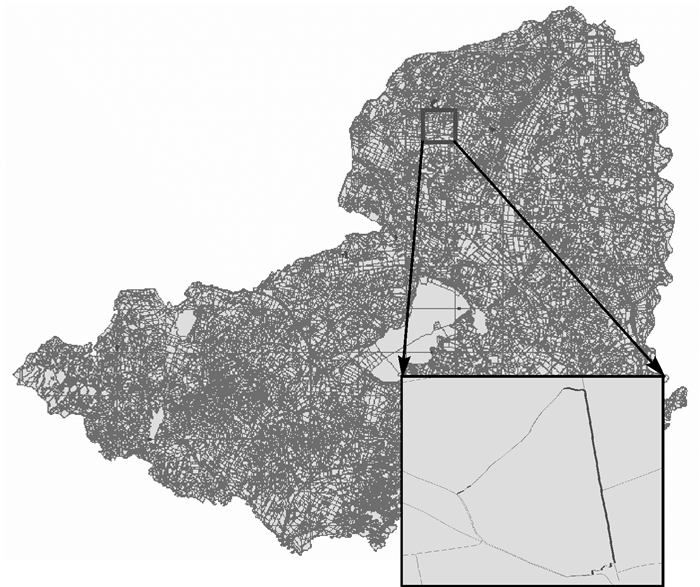
3.3 商业软件对比分析采用第1组宗地数据进行宗地多边形的重叠检查,共有9处重叠区域,其与ArcGIS计算结果一致(如图 5所示)。在相同的硬件环境下,多次运行ArcGIS拓扑计算工具的平均耗时为51 s,而本文并行拓扑计算的多次运行平均耗时为15 s,相比ArcGIS拓扑计算效率提升了3倍。
|
| 图 5 宗地数据重叠检查运行结果 |
如表 3所示,在相同计算环境、不同进程数时宗地重叠拓扑检查的耗时最坏差率不超过6.5%,表明本文并行算法可实现地籍数据中的宗地拓扑叠加质量检查的负载基本均衡与任务基本均衡。随着进程数的增多、各个进程计算量的减少,计算耗时降低、耗时差率越大,反之则表明计算的数据量越大、耗时差率越小,耗时差率与数据量的大小呈负相关性,即在大数据环境下,应用本文方法实现矢量算法并行计算,可更有效解决负载均衡与任务均衡。
| 进程总数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 最长耗时/s | 3214 | 1893 | 1304 | 981 | 788 | 671 | 567 | 506 | 439 | 405 | 373 | 322 |
| 最短耗时/s | 3214 | 1909 | 1298 | 976 | 770 | 653 | 551 | 478 | 427 | 385 | 350 | 339 |
| 耗时差率/(%) | 0 | 0.8 | 0.4 | 0.5 | 2.3 | 2.7 | 2.9 | 5.8 | 2.8 | 5.1 | 6.5 | 5.2 |
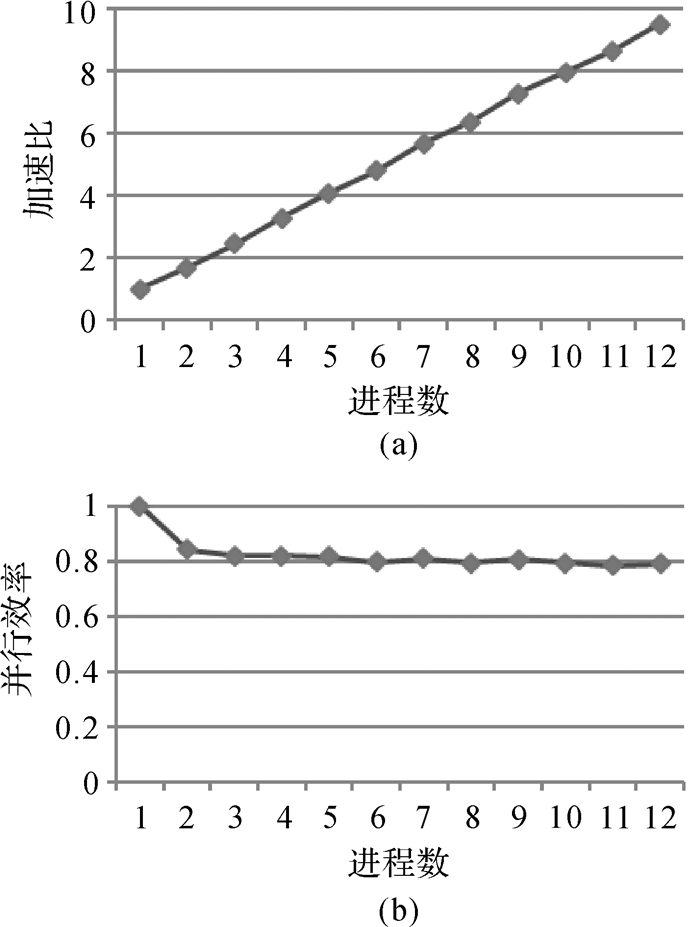
由矢量拓扑关系并行计算加速比、并行效率(如图 6所示)可见:加速比与进程数呈线性正相关,在12个进程时加速比达到9.5倍,拓扑并行算法的计算效率稳定在80%(斜率约为0.8)。
|
| 图 6 拓扑关系并行算法的加速比和并行效率 |
数据划分时间与拓扑关系计算的时间对比见表 4。通过对数据层划分并建立Q&R并行索引实现拓扑关系计算的并行化,所耗费的时间远小于任务执行总时间(输入、计算与输出总时间)。由此可知,基于空间索引的数据划分与数据调度方法,可有效实现拓扑关系计算的并行化。
| 进程总数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 数据划分/s | 35.91 | 36.13 | 37.23 | 37.44 | 37.76 | 38.34 | 38.51 | 38.92 | 39.46 | 39.78 | 40.38 | 40.43 |
| 总时间/s | 3214 | 1909 | 1304 | 981 | 788 | 671 | 567 | 506 | 439 | 405 | 373 | 339 |
| 比率/(%) | 1.12 | 1.89 | 2.85 | 3.81 | 4.79 | 5.71 | 6.79 | 7.69 | 8.98 | 9.82 | 10.82 | 11.92 |
本文针对云环境下地籍数据拓扑关系质量检查算法并行化进行了研究与探索,通过引入Q&R并行空间索引实现了拓扑计算前的数据划分和拓扑计算过程中的数据过滤,基本解决了拓扑计算任务均衡和负载均衡,并且提升了拓扑并行计算的效率,使其并行效率达到80%。基于复杂度较高的地籍(宗地)数据,对拓扑并行算法进行了应用测试,验证了本文方法的可行性与优势性,也为其他矢量数据计算分析的并行化研究提供了参考和思路。本文空间拓扑并行算法支持云平台下的虚拟化集群部署与运行,包括单机多核、集群等多种高性能环境,但在不同环境中仍需要考虑网络通信、存储和计算对空间并行算法的影响,可作为后续的研究方向。
| [1] | 李清泉, 李德仁. 大数据GIS[J]. 武汉大学学报(信息科学版), 2014, 39(6): 641–644. |
| [2] | 吴长彬, 闾国年, 舒飞跃. 基于知识与规则的地籍数据质量检查方法[J]. 地理与地理信息科学, 2007, 23(5): 22–25. DOI:10.3969/j.issn.1672-0504.2007.05.005 |
| [3] | 周晓光. 基于拓扑关系的地籍数据库增量更新方法研究[J]. 测绘学报, 2005, 34(4): 372–372. DOI:10.3321/j.issn:1001-1595.2005.04.017 |
| [4] | 杨宜舟, 吴立新, 郭甲腾, 等. 地籍数据库点线拓扑一致性并行检查方法[J]. 国防科技大学学报, 2015, 37(5): 40–46. |
| [5] | 吴立新, 杨宜舟, 秦承志, 等. 面向新型硬件构架的新一代GIS基础并行算法研究[J]. 地理与地理信息科学, 2013, 29(4): 1–8. |
| [6] | 艾贝贝, 秦承志, 朱阿兴. 栅格地理计算并行算子对区域计算算法并行化的可用性分析——以多流向算法为例[J]. 地球信息科学, 2015, 17(5): 562–567. |
| [7] | 杨宜舟, 吴立新, 郭甲腾, 等. 一种实现拓扑关系高效并行计算的矢量数据划分方法[J]. 地理与地理信息科学, 2013, 29(4): 25–29. |
| [8] | 卢浩, 王少华, 钟耳顺, 等. 一种面向大规模空间数据的拓扑关系检查算法[J]. 地理与地理信息科学, 2014, 30(5): 17–21. DOI:10.3969/j.issn.1672-0504.2014.05.004 |
| [9] | NATHAN T K. Alternative Approaches to Parallel GIS Processing[D]. Phoenix: Arizona State University, 2009: 6-15. |
| [10] | BHAT M A, SHAH R M, AHMAD B. Cloud Computing:A Solution to Geographical Information Systems(GIS)[J]. International Journal on Computer Science and Engineering, 2011, 3(2): 594–600. |
| [11] | YANG C, RASKIN R. Introduction to Distributed Geographic Information Processing Research[J]. International Journal of Geographical Information Science, 2009, 23(5): 553–560. DOI:10.1080/13658810902733682 |
| [12] | YANG Chaowei, XU Yan, NEBERT D. Redefining the Possibility of Digital Earth and Geosciences with Spatial Cloud Computing[J]. International Journal of Digital Earth, 2013, 6(4): 297–312. DOI:10.1080/17538947.2013.769783 |
| [13] | YANG Chaowei, YU Manzhu, HU Fei, et al. Utilizing Cloud Computing to Address Big Geospatial Data Challenges[J]. Computers, Environment and Urban Systems, 2017, 61: 187–197. DOI:10.1016/j.compenvurbsys.2014.01.001 |
| [14] | 张林波. 并行计算导论[M]. 北京: 清华大学出版社, 2006: 50-62. |


