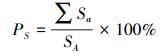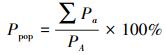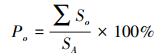城市应急避难场所是指灾害发生后,民众可以集中避难生活,救援工作可以快速开展的场地[1]。国内外学者对避难场所的选址模型已有一定研究,可以将其归为区位选择模型、责任区划分模型和布局优化模型三大类[2]。避难场所的区位选择模型主要为公共设施选址的经典模型及其改进模型[3],常用的有P-中值模型[4]、最大覆盖模型[5]及其改进模型[6]等。该类模型仅考虑传统区位条件,没有顾及选址场地周围因素的影响和能否较好地覆盖居住区等问题。责任区划分模型主要考虑避难场所的服务范围,要求避难场所在此范围内能够满足一定的避难需求[7]。如李刚等提出以Voronoi理论为基础的责任区划分模型[8],李久刚等考虑人口容量、疏散距离等约束条件划定避难场所责任区[9]。该类模型自创建以来进展不大,且在实际应用中没有解决路网、水系等对责任区划分的影响,难以精准地以居民地划分区界。避难场所布局优化模型是根据已有规划文本得出区域内所有避难场所备选点,结合具体的需求对其布局进行优化调整,最终得出最优布局的模型。如吴建宏等建立了多目标规划模型,优化城市所需的避难场所个数、选址和服务区域[10];周亚飞等依据“公平”和“效率”原则建立模型,并利用LINGO进行求解[11];陈文龙等建立了基于Voronoi图和多目标微粒群的空间选址优化模型,智能搜索设施的空间布局位置[12]。该类模型的研究进展较快,考虑的参数越来越多,复杂度越来越大,然而相应的可以实际应用到规划工作中的高效求解算法却相对较少。
现有模型基于各自的选址目标,侧重点各有不同,但都具有一些局限性。本文根据城市规划的流程,综合考虑避难疏散场所个数、区位选择、路径服务长度和人口容量等因素,提出面向城市规划的避难场所选址模型,并开发了基于GIS的避难疏散场所选址分析系统。
1 多条件约束选址模型 1.1 模型需求应急避难场所的规划是在城市总体规划的基础上进行的,其业务流程可分为以下几步:划分综合防灾分区并调查分区内人口分布,分析用地指标与应急避难场所用地资源,分析城市道路情况并组织疏散通道,结合控制性详细规划确定应急避难场所备选点位置,优化调整应急避难场所备选点位置并编写抗震防灾规划。
与业务流程相对应,避难场所的选址一般都是在保证以下4个原则的基础上进行的,即成本最小化、利益最大化、需求导向完善和环境因素符合条件[13]。成本最小化指使疏散人群花费最少代价到达指定场所,如疏散需求点到避难场所的加权总距离最小;利益最大化指避难场所需要服务尽可能多的人口;需求导向完善指避难场所需要满足一定的需求条件,如在规定时间或规定距离内疏散人群必须能够到达避难场所;环境因素符合条件指避难场所的位置需要根据国家规定选在规定的用地类型上,且场所内的设施条件能够保证避难人群的基本生活。
1.2 模型构建针对城市规划的特点和需求,构建多条件约束选址模型,综合已有模型的优势并弥补其不足。避难疏散场所建设首先需要考虑的是成本最小化和利益最大化原则,即模型需要保证每个需求点到与其最近的应急避难场所的距离总和最小且覆盖人口数最大。故模型的主体部分采用区位选址模型,将中值模型和最大覆盖模型的目标函数进行结合。在此基础上,为满足需求导向和环境因素条件,使用责任区划模型添加一系列约束条件;为符合控制性详细规划要求,使用布局优化模型对总规制定的避难疏散场所备选点进行优化调整。
目标函数为
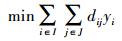 (1)
(1) 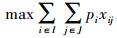 (2)
(2) 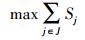 (3)
(3) 约束条件为
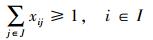 (4)
(4) 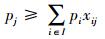 (5)
(5) 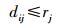 (6)
(6) 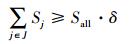 (7)
(7) 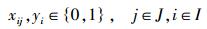 (8)
(8) 式中,I表示需求点的集合{1, 2,…,m}, m为需求点的数目;J表示可利用的应急避难场所的集合{1, 2,…,n},n为应急避难场所的数目;i表示第i个需求点;j表示第j个应急避难场所;dij表示需求点i到应急避难场所j的实际路网距离;pi表示在需求点i处需要被服务的人口数量;Sj表示每个应急避难场所的服务覆盖总面积;pj表示应急避难场所j的最大人口容量;rj表示应急避难场所j的最大服务范围;Sall表示规划区土地总面积;δ表示相关法规规定的应急避难场所总覆盖面积与研究区总面积的最小百分比;
目标函数中,式(1)表示应急避难场所内覆盖的需求点到其距离总和最小,式(2)表示应急避难场所需要覆盖尽可能多的人口,式(3)表示应急避难场所需要覆盖尽可能大的范围。约束条件中,式(4)保证每一需求点都被覆盖到,式(5)保证每个应急避难场所实际容纳的人口都不超过其人口容纳上限,式(6)保证每个需求点至应急避难场所的路径距离不超过该避难场所的最大服务范围,式(7)保证所有应急疏散场所的覆盖面积与规划区总面积之比大于要求的规定比率,式(8)保证xij、yi为二元值变量。
目标函数中,式(1)满足成本最小化原则,式(2)和式(3)满足利益最大化原则,所有约束条件满足需求导向完善原则,环境因素原则在模型具体应用时约束疏散备选点的具体位置。
1.3 评价指标使用模型对规划区域避难疏散场所备选点进行服务范围分析,并据此编写抗震防灾规划。根据《城市抗震防灾规划标准》(GB 50413-2007)及相关文献[14],提出以下评价指标,对避难疏散场所布局的优劣进行评价。
1.3.1 空间覆盖率空间覆盖率PS是指所有应急避难场所覆盖总面积与规划区域总面积的比值,反映应急疏散场所的空间服务能力。
式中,PS为空间服务率;∑Sa为应急避难场所覆盖总面积;SA为规划区域总面积。
1.3.2 人口覆盖率人口覆盖率Ppop是指应急避难场所覆盖范围内人口数与规划区域内总人口数的比值,反映应急避难场所为民众提供服务的情况。
式中,Ppop为人口服务率;∑Pa为应急避难场所覆盖总人口数;PA规划区域总人口数。
1.3.3 服务重叠率服务重叠率Po是指各应急避难场所服务范围与其余应急避难场所服务范围的重叠面积占所有应急避难场所覆盖总面积的比。该值既反映避难场所空间布局的冗余度,又反映各避难场所间相互支援的能力,故应介于一个合理区间之内。
式中,Po为服务重叠率;∑So为各应急避难场所覆盖重叠总面积;SA为规划区域总面积。
2 模型求解现有选址模型已有诸多求解方法,但这些求解方法或过于复杂导致计算时间较长,不适用于规划选址工作实践中,如蚁群算法[15]等;或只能指定固定疏散距离进行选址分析,不能根据区位因素收缩或扩大疏散距离以精确分析疏散场所的布局优劣,如两步移动搜寻法[16]等。
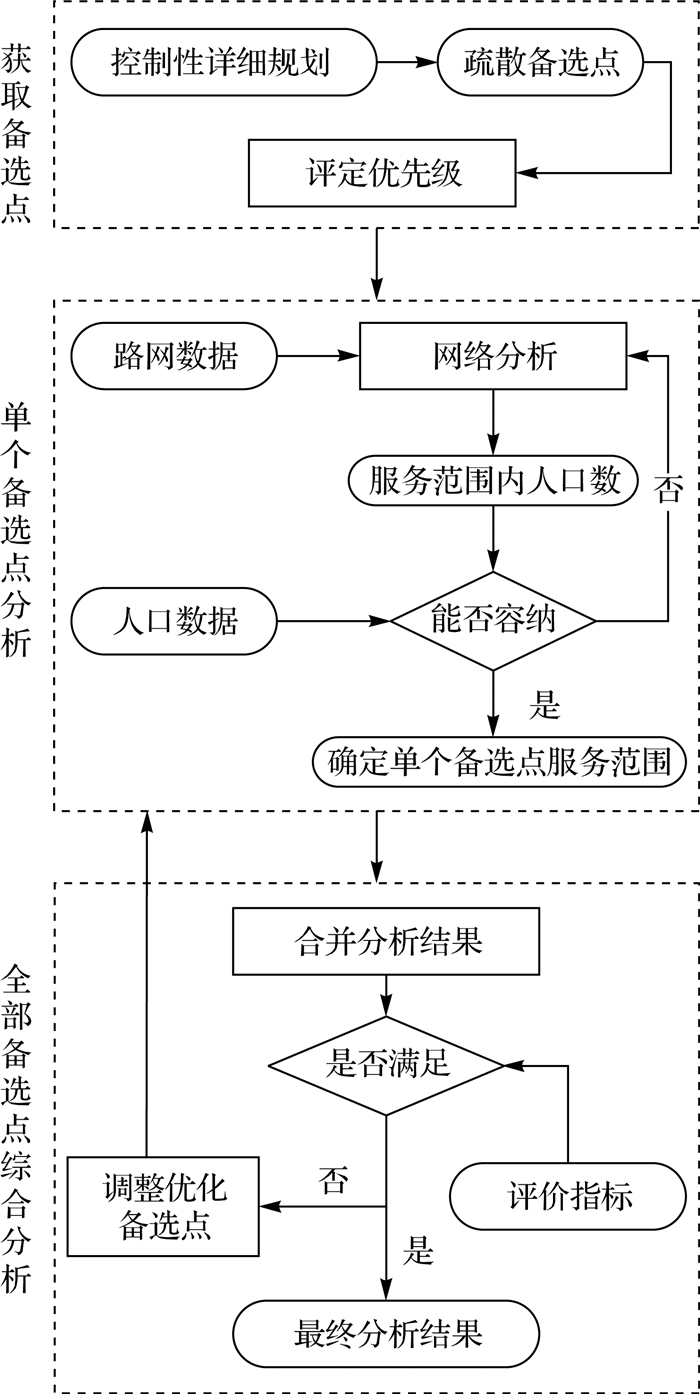
本文的模型求解面向城市规划业务流程,分为3个主要步骤:获取备选点,分析单个备选点和综合优化全部备选点,主要流程如图 1所示。其核心思想是利用迭代算法,在ArcGIS网络分析功能的支持下,以单个备选点为中心进行覆盖范围迭代分析,并对全部备选点进行综合优化。
|
| 图 1 模型求解流程 |
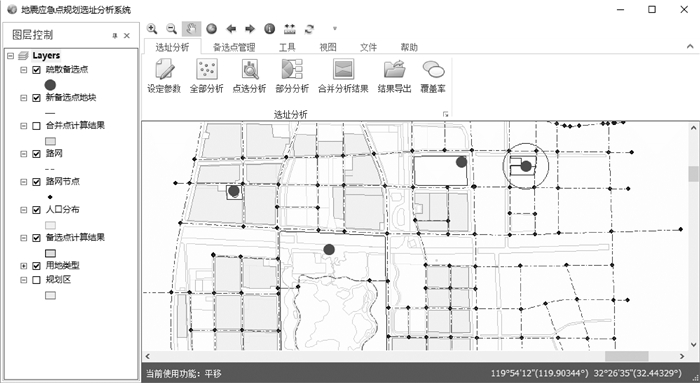
模型求解之前需要准备所需要的数据[17],即获取备选点。根据控制性详细规划初步确定研究区域内疏散备选点的位置及数量,然后按照式(9)优化备选点的数量。其中N为备选点理想数量,K为经验系数,一般取3~6,SA为研究区域总面积,R为避难疏散点最大服务半径。调查分区内人口分布,整理分区内道路数据,并将以上数据全部导入ArcGIS中,转换成GIS支持的数据。根据疏散备选点的空间分布、易改造性、可利用面积、建筑物质量及可开发性评定其优先级,优先级高的备选点优先加入模型计算。
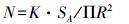 (9)
(9) 然后以单个备选点为中心进行覆盖范围迭代分析。服务范围取决于此避难场所的容量、周边的人口密度及该应急避难场所周围的实际路网。迭代的过程如下:初始计算时,以指定路径长度计算备选点覆盖范围,若覆盖范围内人口数大于该备选点人口容量阈值,则缩小路径长度进行迭代分析,直至覆盖内人口数小于或等于该备选点的人口阈值。如图 2所示,初始2000 m服务范围内人口数量超过容纳量,需要逐步缩小服务范围长度至1600 m,以保证服务区内人口数不超标。最后得出的覆盖范围即为该点的服务范围。
|
| 图 2 单个备选点分析示意图 |
最后为避免陷入局部最优,对全部备选点的分析结果进行综合评价,具体过程如下:依据优先级对各备选点进行分析,分析过程中,不断合并各点的分析结果,并对其进行指标评价。若合并后的分析结果符合各评价指标,则结束求解过程,输出最终分析结果;否则,对备选点的位置及数量进行调整优化,重复以上求解步骤。
3 模型应用根据模型及其求解过程,应用Visual C# 2012及ArcGIS Engine 10.2开发工具对系统进行开发。开发过程中,遵循模块化的编程思想[18],对系统功能进行逻辑划分,可划分出3个主要模块:地图操作模块、选址分析模块、备选点管理模块。系统的主要界面如图 3所示。
|
| 图 3 系统主要界面 |
本文选取江苏省泰州市周山河地区作为研究区域,结合其控制性详细规划对模型和系统进行应用。该规划区域总面积13.65 km2,总人口约25万人。通过前期的数据统计,该地区主要有80个居民地地块,10个可作为疏散备选点的地块。
首先通过计算得出,该区域避难疏散场所备选点的最佳数量为7。通过专业人员的现场踏勘,确定各备选点的位置信息及属性信息如表 1和图 4所示。
| 备选点 | 备选点名称 | 占地面积/m2 | 有效率 | 有效面积/m2 | 最大人口容量 |
| 1 | 体育场馆 | 248 115 | 0.7 | 173 680 | 86 840 |
| 2 | 天德湖公园 | 1 245 800 | 0.2 | 249 160 | 124 580 |
| 3 | G1疏散场所 | 93 600 | 0.8 | 74 880 | 37 440 |
| 4 | 泰州市新区人民医院 | 37 770 | 0.4 | 15 108 | 7554 |
| 5 | 规划中小学 | 108 000 | 0.4 | 43 200 | 21 600 |
| 6 | 居民区疏散场所 | 19 700 | 0.4 | 7880 | 3940 |
| 7 | 拟建设疏散场所 | 61425 | 0.4 | 24 570 | 12 285 |
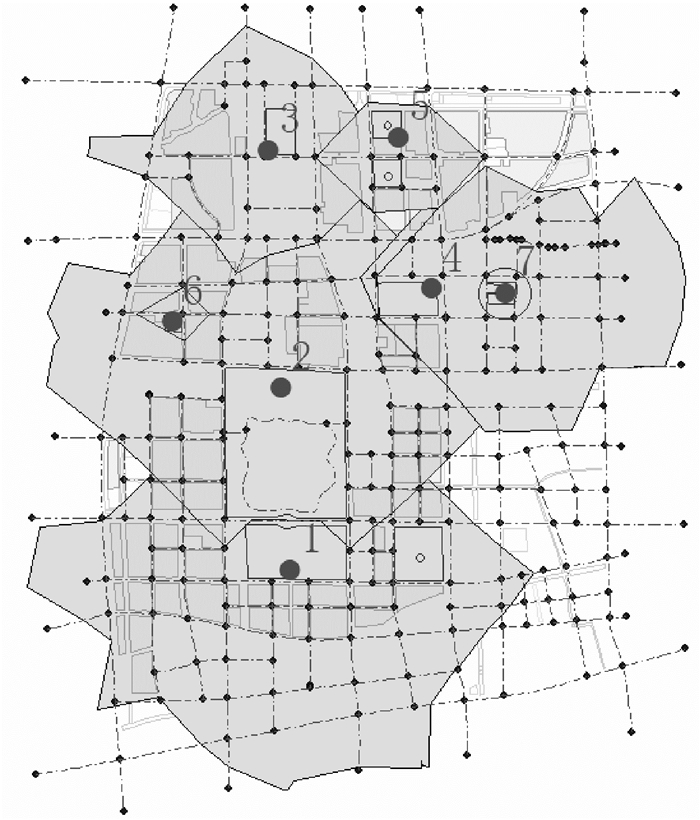
|
| 图 4 初始备选点分析结果 |
将数据导入系统后进行计算分析,得出各避难场所覆盖范围如图 4所示。其中圆点为疏散备选点,浅灰色块状区域为带有人口数据的居民区,灰色块状区域为备选点的覆盖范围。
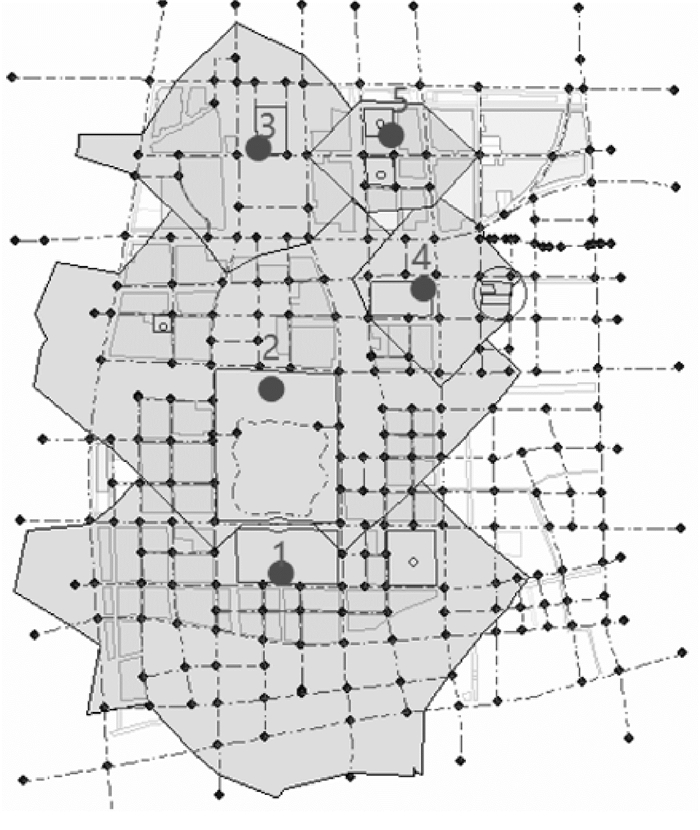
图 4中,6号点的覆盖范围完全被2号点覆盖,故剔除6号备选点;4号点与7号点服务范围重叠度较高,且7号点离居民区较远、覆盖的多为规划区以外的区域,故剔除7号备选点。对修改后的避难场所备选点重新进行分析,结果如图 5所示,评价指标见表 2。依据《泰州市周山河新城控制性详细规划》要求、已有案例及专家经验,人口覆盖空间覆盖率合格阈值为85%,服务重叠率合格区间为15%~25%。修改后结果人口覆盖率和空间覆盖率超过85%,服务重叠率处于15%~25%之间,通过了由住建局、规划局和地震局专家组的认证,可认为该区域疏散备选点布局的合格。
|
| 图 5 修改后备选点分析结果 |
本文根据避难疏散场所的规划流程和选址原则,构建了面向城市规划的应急避难场所选址模型,并提出了人口覆盖、空间覆盖率和服务重叠率3个评价指标。模型整合区位选择模型、责任区划分模型和布局优化模型的优点,综合考虑避难疏散场所个数、区位选择、路径服务长度和人口容量等影响因子,提出了多目标函数和多约束条件。结合城市规划的业务流程提出了迭代求解算法,以实际路网为基础,在ArcGIS网络分析功能支持下对避难疏散场所服务范围进行了分析。根据求解算法建立了避难疏散场所选址分析系统,分析避难疏散场所的优劣并进行了调整。系统成功应用到泰州市周山河新城抗震防灾规划工作中,验证了本文提出的模型的可行性与实用性,可为城市避难场所的规划和建设提供参考。
| [1] | 刘本玉, 叶燎原, 苏经宇. 城市抗震防灾规划的研究与展望[J]. 世界地震工程, 2008, 24(1): 68–72. |
| [2] | 初建宇, 陈灵利. 防灾避难场所选址规划研究综述[J]. 世界地震工程, 2014, 30(1): 139–144. |
| [3] | 宋正娜, 陈雯, 袁丰, 等. 公共设施区位理论及其相关研究述评[J]. 地理科学进展, 2010, 29(12): 1499–1508. DOI:10.11820/dlkxjz.2010.12.005 |
| [4] | HAKIMI S L. Optimum Locations of Switching Centers and the Absolute Centers and Medians of a Graph[J]. Operations Research, 1964(12): 450–459. |
| [5] | CHURCH R L, REVEILLE C S. Theoretical and Computa-tional Links Between the p-median Location Set-covering and the Maximal Covering Location Problem[J]. Geographical Analysis, 1976, 8(4): 406–415. |
| [6] | 周晓猛, 刘茂, 王阳. 紧急避难场所优化布局理论研究[J]. 安全与环境学报, 2006, 6(S1): 118–121. |
| [7] | 马丹祥, 苏幼坡, 初建宇, 等. 基于双层规划的避难场所选址与责任区划分模型[J]. 世界地震工程, 2015(4): 139–145. |
| [8] | 李刚, 马东辉, 苏经宇, 等. 城市地震应急避难场所规划方法研究[J]. 北京工业大学学报, 2006, 32(9): 901–906. |
| [9] | 李久刚, 唐新明, 刘正军, 等. 基于行程距离最优及容量受限的避难所分配算法研究[J]. 测绘学报, 2011, 40(4): 489–494. |
| [10] | 吴健宏, 翁文国. 应急避难场所的选址决策支持系统[J]. 清华大学学报(自然科学版), 2011, 51(5): 632–636. |
| [11] | 周亚飞, 刘茂, 王丽. 基于多目标规划的城市避难场所选址研究[J]. 安全与环境学报, 2010, 10(3): 205–209. DOI:10.3969/j.issn.1009-6094.2010.03.048 |
| [12] | 陈文龙, 安聪荣, 王结臣, 等. 基于网络Voronoi图和多目标微粒群的空间选址优化[J]. 地理与地理信息科学, 2014, 30(3): 1–6. |
| [13] | CURRENT J, MIN H, SCHILLING D. Multiobjective Analysis of Facility Location Decisions[J]. European Journal of Operational Research, 1990, 49(3): 295–307. DOI:10.1016/0377-2217(90)90401-V |
| [14] | 杨文斌, 韩世文, 张敬军, 等. 地震应急避难场所的规划建设与城市防灾[J]. 自然灾害学报, 2004, 13(1): 126–131. DOI:10.3969/j.issn.1004-4574.2004.01.020 |
| [15] | 赵元, 张新长, 康停军. 并行蚁群算法及其在区位选址中的应用[J]. 测绘学报, 2010, 39(3): 322–327. |
| [16] | 周爱华, 张景秋, 张远索, 等. GIS下的北京城区应急避难场所空间布局与可达性研究[J]. 测绘通报, 2016(1): 111–114. |
| [17] | 齐立新, 张新长, 郭泰圣. 规划数据的整理与分类研究[J]. 测绘通报, 2013(8): 28–32. |
| [18] | 谢超, 陈毓芬, 王英杰, 等. 基于模块化的电子地图自适应设计机制研究[J]. 武汉大学学报(信息科学版), 2010, 35(10): 1255–1259. |