随着三维扫描技术的快速发展,点云配准成为一个研究热点,目前已在图像融合、医学研究、文物修复、颅面复原等领域[1-6]得到了广泛应用。颅骨配准是颅面复原的一个重要步骤,其配准精度将直接影响到颅面复原的正确性。颅骨配准的基本思路为:对于一个未知颅骨U,将其与颅骨数据库中已有的多个颅骨进行配准,以找出一个或多个与U最为相似的参考颅骨S,那么参考颅骨S的面貌即可作为未知颅骨U的参考面貌。
通常,扫描仪获取的三维颅骨点云数据量较大,而且不同扫描仪的分辨率差异较大,因此对颅骨配准的精度要求较高。目前,特征点标定法[7-8]是使用较多的颅骨配准方法,但是配准结果并不十分理想。为了提高不同分辨率的颅骨配准精度,提出一种由粗到细的层次化颅骨配准方法。颅骨粗配准就是将两个颅骨通过旋转和平移,变换到同一坐标系下的过程,实现颅骨的初始粗对齐。目前的颅骨粗配准算法大多采用基于特征的配准算法,如颅骨的区域特征、法向和曲率特征以及二维图像特征等[9-11]。这些基于特征的配准算法可以将两个颅骨基本对齐,为接下来的细配准提供良好的初始位置。颅骨细配准就是将两个经过粗配准后的颅骨进行进一步精确对齐的过程。目前,采用最为广泛的颅骨细配准算法是迭代最近点(iterative closest point,ICP)算法[12]或其改进算法[13-16]。
以上这些算法可以在一定程度上提高颅骨配准的精度和速度,但对分辨率差异较大情况下的颅骨点云模型配准效果不佳。为了提高分辨率差异较大颅骨的配准精度和速度,提出一种先粗配准再细配准的层次化颅骨配准方法。首先采用基于NN的配准算法实现颅骨粗配准,然后采用添加模拟退火系数的改进ICP算法实现颅骨细配准,以提高颅骨配准的精度和速度,从而实现颅骨的最终精确配准。
1 基于NN的颅骨粗配准对于待配准的颅骨U和S,假设其对应的点云模型的点集分别为X={x1, x2, …, xM}和Y={y1, y2, …, yN},xi, yj∈Rn,M和N分别为点集X和Y中的点数,n为点云的维度。对于颅骨U和S,其粗配准采用基于NN的点云配准方法来实现。
基于NN点云配准算法的步骤如下:
(1) 建立一个两层的NN,其激励函数为线性函数y=x,训练函数为trainlm函数,trainlm采用Levenberg-Marquardt优化技术来更新权值和偏差。
(2) 训练该NN以获取其连接权矩阵W和偏差矢量b。
(3)基于步骤(2)获取的权矩阵W和偏差矢量b,计算旋转矩阵R和平移矢量t。
(4) 应用刚体变换参数R和t将点集X和Y进行配准。
基于NN的点云配准算法要求|X|=|Y|,即M=N,因此在对颅骨U和S粗配准前,先要对其采样,以使点云X和Y具有相同的点数。该算法的核心问题即根据输入点云X和期待的输出点云Y计算其最佳刚体变换,即旋转矩阵R和平移矢量t。
该算法的特点是:神经网络可以随机初始化权值和偏差,它仅依赖预定义的训练数据来建立刚体变换,因此输入的矢量点和输出的矢量点是一一对应的,并且这种一一对应关系保持不变。因此,基于NN的点云配准算法的相应训练数据的精度越高,配准性能也就越好。
2 基于改进ICP的颅骨细配准 2.1 ICP算法对于两个待配准的颅骨U和S,假设其点云模型对应的点集分别为X和Y。采用ICP算法将X和Y进行配准的步骤如下:
(1) 对于任意一点yj,yj∈Y,j=1, 2, …, N,在X中寻找其欧几里德最近点xi,得到相关点集NY(X)={xi|d(yj, xi)=argminx∈Xd(yj, x)}。
(2) 对于点集NY(X)和Y,采用主成分分析法(PCA)计算其旋转矩阵Rk和平移矢量tk,并应用变换(Rk, tk)来更新点集Y,从而得到刚体变换参数R和t,其计算式为
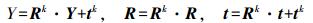 (1)
(1) 重复步骤(1)和(2),直到满足算法的终止迭代条件为止。
ICP算法是一种精度较高的点云配准算法,但它要求两个点集之间存在包含关系,并且对大数据量点云的配准速度较慢,而且没有考虑不同尺度点云的配准问题。鉴于此,在颅骨U和S的细配准过程中,采用一种添加尺度因子和模拟退火系数的改进ICP算法来实现颅骨的细配准。
2.2 改进ICP算法 2.2.1 求解刚体变换颅骨U和S的配准问题就是寻求点集X和Y的最佳变换F的过程,也即使得∑||X-F(y)||2尽可能小。在ICP算法中加入尺度因子后,点集X和Y的配准问题就转换为式(2)的优化问题
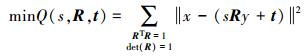 (2)
(2) 式中,s为尺度因子。
假设X={x1, x2, …, xM}和Y={y1, y2, …, yN}含相同数目的点,于是式(2)可简化为
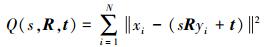 (3)
(3) 对式(3)求解关于t的偏导数,并使其为0,则可以计算出平移矢量t的值为
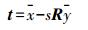 (4)
(4) 式中,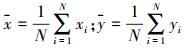
于是,式(3)可进一步表示为
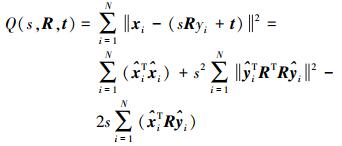 (5)
(5) 采用矩阵的迹,目标函数可进一步写为
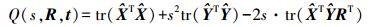 (6)
(6) 式中,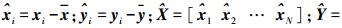
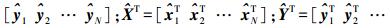
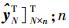
令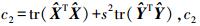
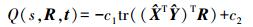 (7)
(7) 令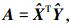
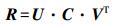 (8)
(8) 式中,C=d(1,1,…,1,det(U·VT))。
下面对式(7)求解关于s的偏导数,并令其为0,则尺度因子s的值为
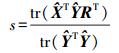 (9)
(9) 由此得到刚体变换的旋转矩阵R、平移矢量t和尺度因子s。
2.2.2 改进ICP算法的步骤改进ICP算法将模拟退火的思想加入ICP算法中,可以大大提高颅骨点云模型的配准精度和速度。首先定义一个温度参数α,它表示子集的数目。在ICP算法的每次迭代过程中,α都要进行加1操作。
对于颅骨U和S对应的点集X和Y,改进ICP算法对其配准的步骤描述如下:
(1) 设置参数的初值,即尺度因子s0=1,旋转矩阵R0=I,平移矢量t0=0,模拟退火因子α=1。
(2) 基于ICP算法的点的相关性求解方法,建立子集Xα和Yα的相关性。
(3) 采用式(4)、式(8)和式(9)求解刚体变换参数R、t和s。
(4) 应用刚体变换参数R、t和s到点集Y上。
重复步骤(1)-(4),直到达到算法终止条件为止。
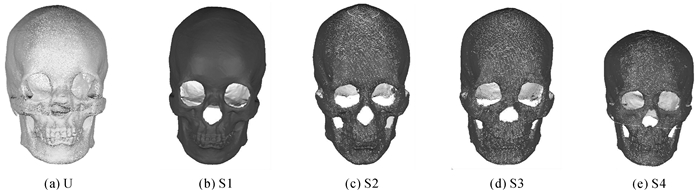
3 试验结果与分析试验采用西北大学可视化技术研究所提供的颅骨点云数据模型进行颅骨配准测试。对于图 1(a)所示的未知颅骨U,将其与颅骨库中300个完整的颅骨进行配准。未知颅骨U与某一参考颅骨S的配准过程为:首先对颅骨U和S进行去噪、简化和归一化等预处理[17],并使它们有相同数量的采样点;然后采用基于NN的点云配准算法实现两个颅骨的粗配准;最后采用改进的ICP算法实现颅骨U和S的细配准。
|
| 图 1 未知颅骨U及部分参考颅骨S1-S4 |
通过将未知颅骨U与300个颅骨进行配准,找到了U的一个最为相似的参考颅骨S1,如图 1(b)所示,部分不能正确配准的颅骨如图 1(c)-(e)所示。从图 1可见,显然颅骨S1比S2、S3、S4具有更高的分辨率,而且颅骨S4的尺度更小。未知颅骨U与颅骨S1-S4的配准结果如图 2所示。
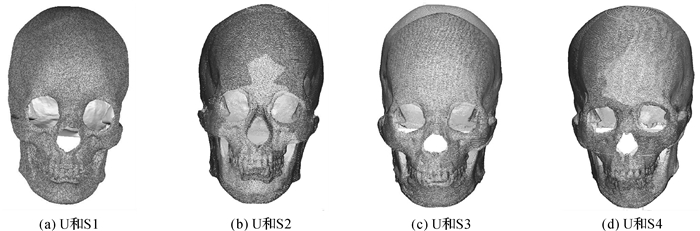
|
| 图 2 U和S1-S4的配准结果 |
从图 2的配准结果来看,未知颅骨U和颅骨S1可以正确配准,和颅骨S2、S3、S4不能正确配准。因此,颅骨S1就可以作为未知颅骨U的参考颅骨,即参考颅骨S1的面貌即可作为未知颅骨U的复原参考面貌。为了进一步验证该改进ICP算法在配准精度和速度方面的性能,基于前面粗配准的结果,再分别采用ICP算法、ICP-DAF算法[18]和WICP算法[14]进行颅骨细配准。4种细配准算法的配准结果见表 1。
| 未知颅骨(点云数目) | 参考颅骨(点云数目) | 算法 | 配准误差/mm | 迭代次数 | 耗时/s |
| U(201 962) | R1(417 897) | ICP | 0.006 8 | 69 | 6.26 |
| ICP-DAF | 0.006 9 | 35 | 3.14 | ||
| WICP | 0.005 4 | 49 | 4.39 | ||
| 改进ICP | 0.004 8 | 36 | 3.15 | ||
| R2(210 416) | ICP | 0.009 6 | 70 | 6.28 | |
| ICP-DAF | 0.009 8 | 36 | 3.15 | ||
| WICP | 0.007 9 | 50 | 4.41 | ||
| 改进ICP | 0.006 7 | 36 | 3.16 | ||
| R3(301 492) | ICP | 0.009 8 | 72 | 6.33 | |
| ICP-DAF | 0.010 1 | 37 | 3.17 | ||
| WICP | 0.008 1 | 51 | 4.43 | ||
| 改进ICP | 0.006 9 | 37 | 3.19 | ||
| R4(157 113) | ICP | 0.010 1 | 64 | 5.94 | |
| ICP-DAF | 0.010 5 | 32 | 2.93 | ||
| WICP | 0.008 1 | 45 | 4.16 | ||
| 改进ICP | 0.007 2 | 33 | 2.95 |
颅骨配准是颅面复原的一个重要步骤,其配准精度将直接影响到颅面复原的正确性。为了提高颅骨配准的精度和速度,本文提出一种先粗配准再细配准的层次化颅骨点云配准方法。首先采用基于NN的点云配准算法实现颅骨粗配准,然后采用添加了模拟退火系数的改进ICP算法实现颅骨的细配准。与ICP算法相比,该改进ICP算法具有更高的配准精度和速度,可以实现颅骨的最终精确配准。因此可以认为该由粗到细点云配准方法是一种有效的颅骨配准方法。但是由于该方法没有考虑噪声和外点对配准的影响,因此对噪声含量较大的颅骨配准效果不佳。在今后的研究中,需要进一步考虑噪声、外点、存在颅骨缺损等多种因素对颅骨配准结果的影响,提出更加快速、高精度、稳健性强的颅骨配准方法,并将其应用于颅骨面貌复原研究中。
| [1] | ZHOU C, ANSCHUETZ L, WESER S, et al. Surface Matching for High-accuracy Registration of the Lateral Skull Base[J]. International Journal of Computer Assisted Radiology and Surgery, 2016, 11(11): 1–7. |
| [2] | SONG Z, JIANG H, YANG Q, et al. A Registration Method Based on Contour Point Cloud for 3D Whole-body PET and CT Images[J]. BioMed Research International, 2017(2): 1–11. |
| [3] | GRODZICKI P, CAPUT M. Entropy-based Registration of Point Clouds Using Terrestrial Laser Scanning and Smartphone GPS[J]. Sensors, 2017, 17(1): 229–239. |
| [4] | CUI T, JI S, SHAN J, et al. Line-based Registration of Panoramic Images and LiDAR Point Clouds for Mobile Mapping[J]. Sensors, 2017, 17(1): 70–89. |
| [5] | 郑敏辉, 臧玉府, 梁福逊, 等. 不同场景的地面激光点云配准方法研究[J]. 测绘通报, 2015(8): 30–34. |
| [6] | 盛庆红, 陈姝文, 柳建锋, 等. 基于Plücker直线LiDAR点云配准法[J]. 测绘学报, 2016, 45(1): 58–64. |
| [7] | 冯筠, 陈雨, 仝鑫龙, 等. 三维颅骨特征点的自动标定[J]. 光学精密工程, 2014, 22(5): 1388–1394. |
| [8] | LINDEBERG T. Scale Selection Properties of Generalized Scale-space Interest Point Detectors[J]. Journal of Mathematical Imaging and Vision, 2013, 46(2): 177–210. DOI:10.1007/s10851-012-0378-3 |
| [9] | CAO Z C, MA F L, FU Y L, et al. A Scale Invariant Interest Point Detector in Gabor Based Energy Space[J]. Acta Automatica Sinica, 2014, 40(10): 2356–2363. DOI:10.1016/S1874-1029(14)60364-5 |
| [10] | IZUMIYA S, NABARRO A C, SACRAMENTO A D J. Pseudo-spherical Normal Darboux Images of Curves on a Timelike Surface in Three Dimensional Lorentz Minkowski Space[J]. Journal of Geometry and Physics, 2015, 97: 105–118. DOI:10.1016/j.geomphys.2015.07.014 |
| [11] | LIN C C, TAI Y C, LEE J J, et al. A Novel Point Cloud Registration Using 2D Image Features[J]. Eurasip Journal on Advances in Signal Processing, 2017(1): 5–15. |
| [12] | BESL P J, MCKAY N D. A Method for Registration of 3-D Shapes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 14(2): 239–256. |
| [13] | MARANI R, RENO V, NITTI M, et al. A Modified Iterative Closest Point Algorithm for 3D Point Cloud Registration[J]. Computer-Aided Civil and Infrastructure Engineering, 2016, 31(7): 515–534. DOI:10.1111/mice.12184 |
| [14] | WANG X, ZHAO Z L, CAPPS A G, et al. An Iterative Closest Point Approach for the Registration of Volumetric Human Retina Image Data Obtained by Optical Coherence Tomography[J]. Multimedia Tools and Applications, 2017, 76(5): 6843–6857. DOI:10.1007/s11042-016-3302-9 |
| [15] | DONG J, CAI Z, DU S. Improvement of Affine Iterative Closest Point Algorithm for Partial Registration[J]. IET Computer Vision, 2017, 11(2): 135–144. DOI:10.1049/iet-cvi.2016.0058 |
| [16] | EDLUND O. Robust Registration of Surfaces Using a Refined Iterative Closest Point Algorithm with a Trust Region Approach[J]. Numerical Algorithms, 2016, 74(3): 1–25. |
| [17] | 李广云, 李明磊, 王力, 等. 地面激光扫描点云数据预处理综述[J]. 测绘通报, 2015(11): 1–3. |
| [18] | LI W, SONG P. A Modified ICP Algorithm Based on Dynamic Adjustment Factor for Registration of Point Cloud and CAD Model[J]. Pattern Recognition Letters, 2015, 65(11): 88–94. |


