2. 63883部队, 河南 洛阳 471000
2. 63883 Troop, Luoyang 471000, China
作为一个拥有300多万平方千米海域的海洋大国,高精度、极可靠的海洋大地测量基准能支持我国进行海洋权益维护、海洋经济发展等一系列海洋活动[1]。而海洋大地测量基准的基础,就是要建立起精确可靠的海洋大地测量控制网。1985年斯克里普斯海洋研究所(scripps institution of oceanography, SIO)的Spiess最早提出可以将GNSS/声学定位结合进而实现海底控制点的建立[2],以此原理为基础,逐渐形成了实用性的GNSS/声学定位系统[3]。该系统用实时动态测量船将卫星导航系统和水下定位系统联系起来,利用测量船接收的GNSS观测数据和水下声学测距数据,对海底控制点进行定位,具有设计简单、操作方便快捷、成本相对较低、能得到海底控制点绝对坐标等特点,对我国高精度海洋大地测量控制网的建立和研究具有重要的参考价值。
自20世纪80年代以来,众多学者对GNSS/声学定位系统中的关键技术进行了研究和探索。文献[4-6]研究了系统的数据解算策略和误差处理方法;文献[7-9]使测量船分别处于漂流、圆航迹、三角形航迹状态下进行定位试验,在此基础上,文献[10]说明了均匀分布的航迹线对于提高定位精度的作用。近年来,欧洲、加拿大等地区的海底观测网[11]以及正向全球化发展的地转海洋学实时观测阵(Argo计划)[12],都可以看作是GNSS/声学系统模块的衍生与发展。然而,现有研究大多利用动态差分定位确定海上船载GNSS接收机位置,实际应用中,这种定位方式容易受到作业距离或岸基基准站分布的限制[13]。已有研究证明了动态非差精密单点定位(precise point positioning, PPP)应用于海上定位的可行性[14],但其定位精度和实时应用也受到更多误差因素的制约。
针对目前的研究空白,本文着重讨论了利用PPP进行海上定位时影响GNSS/声学系统定位精度的各类因素,并基于自编软件,进行海底控制点的仿真定位试验,验证部分因素的理论影响。
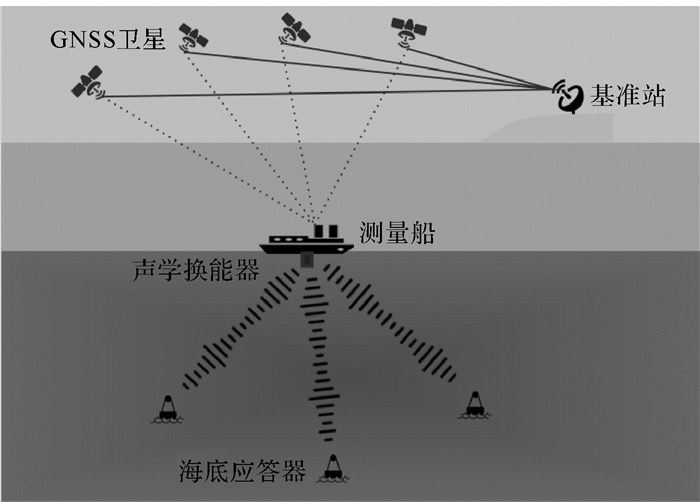
1 GNSS/声学定位系统GNSS/声学系统采用松耦合集成[15]的方案,以海面测量船为媒介,联合GNSS卫星和水下声学测距技术,可以得到全球坐标系统下的海底控制点坐标。该系统包括GNSS卫星星座、GNSS基准站、测量船、海底控制点或应答器。其工作原理如图 1所示。
|
| 图 1 GNSS/声学定位系统工作原理 |
海上采用非差方式进行定位可以不受作业距离的限制,但却无法消除部分误差的影响。观测值选用消电离层组合,结合IGS(International GNSS Service)轨道和钟差产品,海上接收GNSS伪距和载波相位数据进行动态PPP的观测方程如下[16]
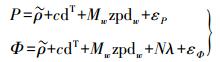 (1)
(1) 式中,P和Φ分别为测码伪距和载波相位观测值;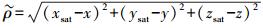
水下声脉冲测距定位观测方程可以概括为[17]
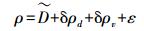 (2)
(2) 式中,ρ为声学信号测量得到的由船底换能器至海底应答器的距离;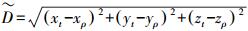
GNSS/声学定位系统实现了两种不同定位方式的结合,将独立工作的两个系统集成到了一个统一的架构下,其定位精度也因此会受到各系统单独定位过程中各类误差因素的制约及系统间数据融合处理方法的影响。此外,系统内主要用于记录数据的GNSS天线、电罗经、惯性元件、换能器等多类传感器,其设备精度也是不可忽视的重要误差来源。
2.1 GNSS动态定位相关影响因素在动态PPP中,观测量采用非差形式,大部分误差无法从数据组合的角度进行消除,若再考虑海上作业环境的特殊性,陆上部分可以不予考虑的误差源,将对海洋定位结果产生较大影响,如大洋负荷,对于靠近海岸进行的短时段观测或较高精度的动态精密单点定位,都需要进行大洋负荷的模型改正[16]。为叙述简洁明了,本文将船载定位中的主要误差统一称为GNSS动态定位误差,即船位精度。通过简单的公式推导可以得出结论:海底应答器定位误差随船位误差的增大而增大,受篇幅所限,具体推导不作详述。作为建立海底控制点的海面基准,对海上GNSS动态定位中的各项误差加以合理的约束和改正,是最终能得到较高精度位置结果的基础。
2.2 测量船相关影响因素 2.2.1 测量船自身影响因素测量船的噪声源大致可分为:①设备机械噪声,指在测量船进行海上作业时,主机、螺旋桨等设备由于自身的运作、附近气流环境的影响等问题所辐射的噪声;②水动力噪声,指海上水流影响所辐射的噪声。其中,前者是更主要的噪声影响,具体哪种设备影响较大则取决于频率、航速、深度等的影响,如测量船处于高航速时,螺旋桨产生的噪声影响更大[18]。
此外,在动态海面环境中,测量船通常安装4类传感器:GNSS天线、电罗经、姿态测量元件和换能器。其中,GNSS天线用于接收卫星GNSS信号,确定船体位置;电罗经用于测定航向参数,确定船体行进方向;姿态测量元件用于测定姿态信息,确定船体瞬时姿态;换能器用于接收和发送声学信号,与海底应答器建立联系。在未进行相应改正之前,其本身的安装误差,也是影响测量结果的一类系统误差。
2.2.2 偏心改正和姿态改正海上利用GNSS天线或船体中心作为参考点进行动态定位,而水下声学定位通过船载换能器与海底应答器进行声学信号的发送和接收,两个定位点间存在角度偏移和距离偏移,为了得到高精度的海底定位结果,需要对这一偏差进行改正,此即为测量船的偏心改正。若忽略这一改正,可以视作海面基准出现偏差。
另一个影响较大的因素来自船体的姿态变化。由于风浪、湍流、海况等环境因素的影响,船体无法像陆地上的动态定位一样平稳地在海平面上进行,GNSS天线也随之发生姿态变化,此时通过卫星确定的定位点将不再准确,因此姿态改正是必须考虑的影响因素。经过姿态改正,海面及水下的各种观测量可以在统一的坐标系下进行讨论,各类船载传感器的位置误差也得到了控制。
2.2.3 测量船航迹或海面基线网无论是航迹或是基线网,都可以看作在k时刻和海底应答器组成了一个几何多面体,在忽略其他误差的情况下,类似单点定位中的精度衰减因子(dilution of precision,DOP),利用瞬时航迹点或浮标位置,可以得到航迹或浮标位置矩阵,其也是直接影响海底应答器定位精度的因素之一。实际上,可把海底应答器视作单点定位中的“测站”,船位或浮标位置视作“卫星”,则控制好二者所构立体图形的几何强度,将是得到高精度海底定位结果的重要环节。
2.2.4 船速、航迹点个数、观测总数假设在海面上选择了一定量的航迹点,在每个航迹点上得到了必要的观测量,则可以得到在此情况下应答器坐标δXρ1及相应的协方差矩阵ΣδXρ1。保证其他条件不变,假设在上述情况的基础上,增加航迹点和相应的观测数量,类似序贯平差的求解方法,可以写出ΣδXρ2。根据矩阵反演公式和相应的求迹运算可以得到
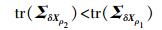 (3)
(3) 式(3)说明,在理论情况下,增加观测数量,可以提高海底应答器定位精度。但实际上,并不是较多的航迹点和观测总数,就一定能保证得到高精度的最终结果。一方面,受测量船自身设备、复杂海洋环境等因素影响,每次航行所计划的航迹点数量需在一定范围内,且过多的航迹点可能会影响海面基线网的几何强度;另一方面,不是每一个航迹点上进行的观测都能保证其数据的可靠性,若增加了观测数据质量较差的航迹点,可能会适得其反,降低应答器的定位精度。因此,应当设计出空间几何图形强度得到保证的较优航迹线,使尽可能多且数据质量高的航迹点参与最终的定位解算。
2.3 水下声学定位相关影响因素声速在海水中会受到温度、盐度、静压力的综合影响,其中温度对声速变化的影响最显著。由于深海区域的温度和盐度分布更稳定均匀,近海面区域的温度有更大的波动范围,因此近海面区域的声速往往在空间和时间上都会出现一定的扰动现象[4],反映出声速结构的不均匀性,也是水下声学传播最主要的影响因素。
声波在海水中传播时会出现能量耗散、被吸收,还受到不均匀的声速结构影响,其速度和方向均会瞬时变化,进而产生声线弯曲的现象,直接影响换能器和应答器间的距离测定。此外,声线弯曲限制了声波传播的有效距离,对于海底应答器选址、基阵图形的设计也有一定影响。在本系统中,一方面可以利用现有经验模型进行声线弯曲改正,另一方面,在进行测量船航迹设计及航迹点选取时,需要考虑设计合理的观测入射角,因为过大的入射角会增大声速结构变化的误差影响[19],从而造成水下观测数据质量偏低。
2.4 应答器相关影响因素除开船载传感器安装误差,若海底应答器以阵列形式布设,则应答器阵列作为一个整体,其性能也是直接影响定位结果的重要因素之一。提升应答器阵列性能,需要考虑如选址、阵的方向性、构型设计等问题。首先,对应答器阵列进行合理选址,必须充分考虑声波的有效距离,因为应答器阵列所在海底地形对声信号的有效传播距离也有一定影响[20]。在有一定坡度的海底地段,若应答器阵列沿坡布设,海面测量船在此海域航行过程中,其声波有效距离可能会不停改变,不利于声学信号的捕捉。其次,类似船体姿态变化的影响,应答器阵列的方向性若不合适,无法避开一些强干扰源,将会影响声学信号的接收和发射。在选择出能够进行自适应调整的应答器或进行了充分的安装校准后,可以忽略其对整个系统的影响。最后,阵列的构型决定海底应答器位置的校准误差[21],且合理的构型可以减弱声学测距误差,因此需要依据声波有效距离,结合海面船航迹进行海底阵型的最优设计。
2.5 其他影响因素 2.5.1 偶然误差影响包括信号识别和探测的影响、GNSS观测值误差、声学观测值误差、传感器量测误差、测时误差等。其中,信号探测的精度主要取决于声学信号被其他误差扭曲的程度;高精度设备可以控制各类量测误差。
2.5.2 时间配准GNSS/声学系统定位过程中包括多类观测数据:GNSS数据、航向数据、姿态数据、声学数据等。经过偏心和姿态改正,可以在统一的坐标系下进行解算,但由于不同数据的采样率、频率等也不同,还需要通过时间插值、延迟确定相关经验模型[22]实现数据间时间的一致性。
3 仿真试验分析 3.1 仿真环境为了更直观地说明上述误差源对系统定位精度的影响,基于自编软件,模拟了理想状态下GNSS/声学系统的工作环境。受篇幅所限,对定位过程中GNSS动态定位精度、采样率及航迹点个数、应答器阵列构型3种主要影响因素进行了仿真试验验证。试验模型及参数设置见表 1。其中,可以利用文献[17]中提出的估计公式对声学定位中最主要的误差δρv进行模拟。
| 类型 | 处理方法 | |
| 试验模型 | GPS观测值 | 非差消电离层组合 |
| 水下模拟观测值 | 考虑声速变化的系统误差计算的斜距值再加上±5 cm的随机误差 | |
| 卫星高度截止角 | 5° | |
| 卫星星历及钟差 | 采用精密星历和精密钟差 | |
| 其他误差影响 | 考虑海洋潮汐、固体潮、天线相位中心改正、相对论效应 | |
| 参数估计 | 测量船位置参数 | 对GNSS/声学定位模型中的各参数每个历元估计一次。针对3种主要影响因素,分别进行了仿真试验: |
| 接收机钟差 | ||
| 天顶方向对流层延迟 | 试验1:GNSS动态定位精度的影响; 试验2:采样率和航迹点的影响; 试验3:应答器阵列构型的影响 |
|
| 海底模拟点位置参数 | ||
| 模糊度参数 |
海上部分采用2017年9月29日在江苏大丰港某海域,测量船出海约3 h实测的GPS观测数据,采样间隔为1 s。海底模拟点的初始布设参考文献[17]提出的圆阵列方案:假设水下已布设3个控制点,处于海底半径等于水深的同一圆上,其相对位置通过初步测量已经得到。现以模拟圆心为坐标原点建立海底测量坐标系,x轴指向其中一点,使测量船轨迹大致以模拟圆心的海面正投影为中心分布。假设水深1.5 km,换能器每0.2 s记录一次观测值,将已考虑声学系统误差得到的斜距再加上绝对值为5 cm的随机误差,并利用角度关系转换为模拟圆心坐标的平均误差偏离,从而计算得到换能器至模拟圆心的几何“伪斜距”作为参与平差的等效水下模拟观测值。利用高精度GNSS数据处理软件Bernese动态PPP功能对船测数据进行预解算,选取若干点位以确定轨迹的大致中心位置,并将其正投影到“海底”,视为海底模拟点真值坐标,作为与定位结果对比的参考。
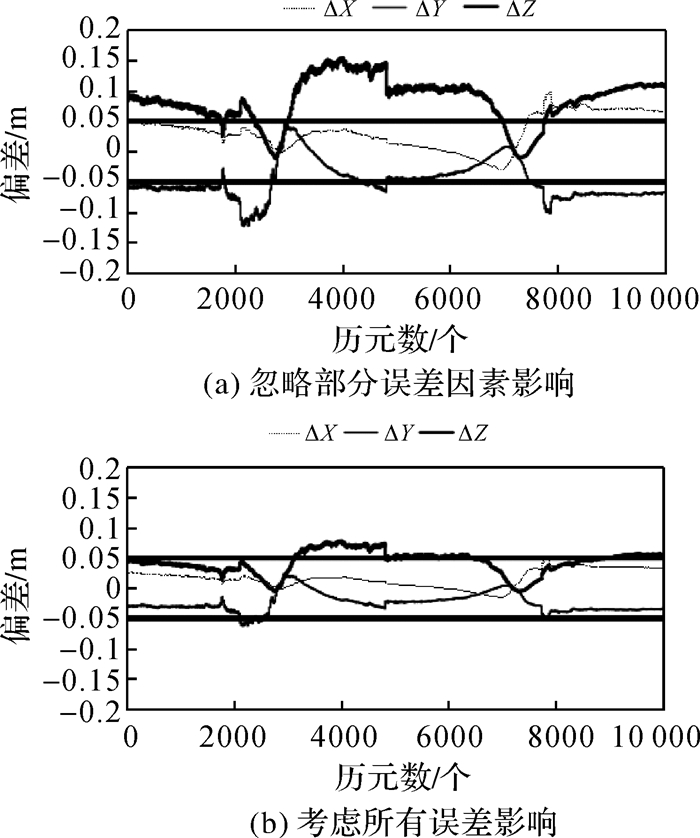
3.2 试验结果分析试验1:①其他条件不变,对海洋潮汐、极潮、天线相位缠绕等陆上厘米级影响的误差因素不进行模型改正,定位结果如图 2(a)所示;②在步骤①的基础上,对所有误差因素进行模型改正,定位结果如图 2(b)所示。
|
| 图 2 GNSS动态定位精度对应答器坐标解算的影响 |
由图中对比可知,若对部分误差因素不建立相应的误差模型加以改正,海底应答器坐标的解算效果将受到较大影响。处理相应误差后,X、Y方向上的定位偏差结果由0.1 m减小至0.05 m,Z方向上可以控制在1 dm以内,3个方向上的定位精度均有不同程度的提高。这与2.1节的结论一致,说明在本系统中,提高海上船载GNSS动态定位精度,将成为得到海底应答器精确坐标的重要步骤之一。
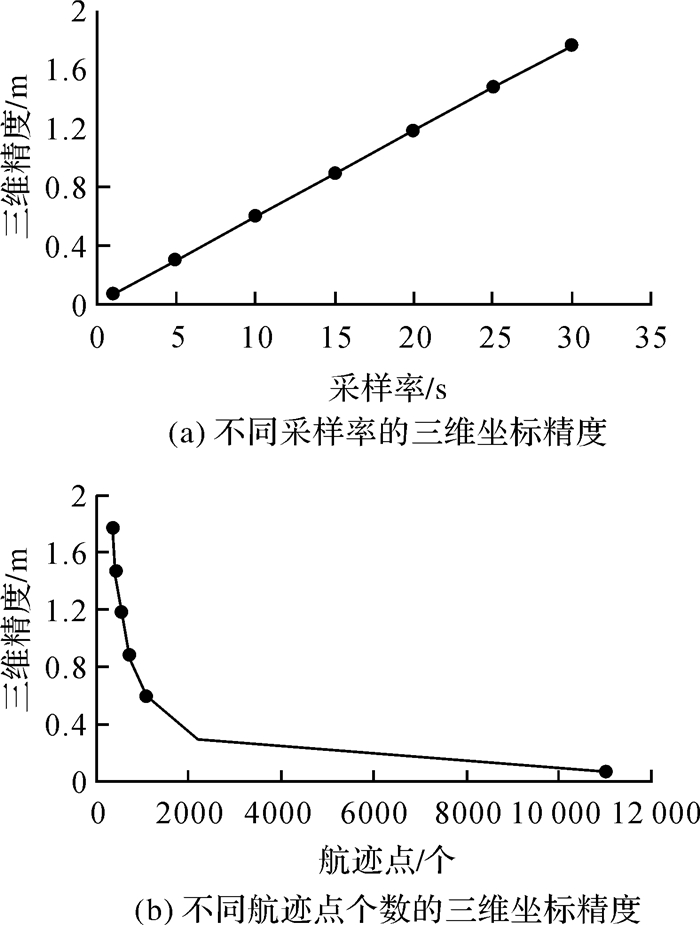
试验2:将原始观测数据的采样率由1 s分别改为5、10、15、20、25、30 s,分析应答器三维坐标精度随采样率和航迹点的变化如图 3所示。
|
| 图 3 采样率和航迹点个数对应答器坐标解算的影响 |
由图 3(a)可知,当采样率为1 s时,海底控制点坐标可达厘米级精度,随着采样间隔的增加,观测总数相应减少,海底控制点三维精度逐渐降低;当采样率为30 s时,应答器位置偏差已接近2 m,表明观测数量在一定程度上也影响着定位结果;由图 3(b)可知,随着航迹点的增多,海上GNSS观测量和海下声学观测量数量也相应增加,海底控制点三维坐标精度有了明显提升。结合2.2.4节分析可以得出结论,在不影响海面基线网-海底应答器空间几何图形强度的前提下,适当增加航迹点和观测数量有助于改善最终的定位结果。
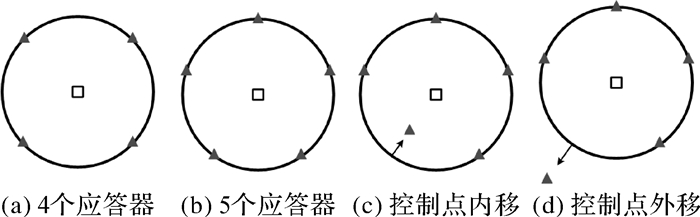
试验3:①在初始仿真的圆阵列基础上,增加1个应答器,即假设海底布设的是相对位置已知的4个控制点,如图 4(a)所示;②在初始仿真的圆阵列基础上,增加2个应答器,即假设海底布设的是相对位置已知的5个控制点,如图 4(b)所示;③在步骤②的基础上,将其中一个控制点的布设位置沿半径向圆心方向移动500 m,如图 4(c)所示;④在步骤②的基础上,将其中一个控制点的布设位置沿半径向远离圆心方向移动500 m,如图 4(d)所示。分别对4种方案各个方向上定位偏差结果的最大值、标准差(standard deviation,STD)及均方根(root mean square,RMS)进行统计(见表 2)。
|
| 图 4 4种不同的海底应答器阵列构型 |
| cm | |||||||||||
| 类别 | 最大偏差 | STD | RMS | ||||||||
| ΔX | ΔY | ΔZ | ΔX | ΔY | ΔZ | ΔX | ΔY | ΔZ | |||
| 3个应答器 | 5.10 | 6.24 | 13.20 | 2.21 | 2.92 | 4.70 | 2.24 | 2.95 | 4.72 | ||
| 4个应答器 | 6.76 | 8.35 | 17.40 | 2.96 | 3.93 | 6.30 | 2.99 | 3.96 | 6.33 | ||
| 5个应答器 | 8.42 | 10.39 | 21.63 | 3.68 | 4.89 | 7.84 | 3.72 | 4.93 | 7.88 | ||
| 控制点内移 | 8.46 | 10.39 | 22.20 | 3.71 | 4.91 | 7.86 | 3.75 | 4.95 | 7.91 | ||
| 控制点外移 | 8.80 | 10.38 | 22.37 | 3.89 | 5.04 | 8.05 | 3.95 | 5.10 | 8.10 | ||
由表中数据可知,应答器阵列的构形不同,其定位结果也有所差异。以本试验所采用的海面测量船轨迹及应答器间相对位置为例,当应答器的分布能保证整个阵列相对于船迹中心的海底投影点有较好的对称性时,其三维精度能优于分米级,如对于等边三角形或正方形构形的应答器分布,以任一应答器和投影点的连线为轴,阵列均为对称图形,可以减弱声学测距误差的影响。对比不同个数应答器的定位结果发现,一味地增加应答器个数并不能提高定位精度,基线长度不合理或空间图形几何强度较差均有可能降低结果可靠程度。此外,得到的虚拟圆心坐标在X、Y方向上的定位偏差结果均优于Z方向,X、Y方向上的标准差和最大偏差统计结果均小于Z方向,推测原因是与本试验设计的圆阵列及测量船运动范围有关,保证应答器布设的对称性和声学信号传播时间的基本一致性,在假设声速只在水深方向变化的前提下,可以认为δρv在模拟圆心水平方向坐标的影响较小。
4 结论本文介绍了目前在海底控制点的建立中被广泛运用的GNSS/声学定位系统,在采用非差方式进行测量船位置确定的前提下,详细分析了组合式系统定位过程中可能存在的各类影响因素,从理论原理的角度推导了部分具体的误差影响,并基于自编软件,利用仿真试验验证了相应结论。试验模拟了GNSS/声学定位环境,采用2017年9月29日在江苏大丰港某海域约3 h的实测数据及模拟的水下测距数据,分别验证了3类主要误差因素对定位结果的影响,由试验结果可以发现:
(1) 作为系统确定海底应答器位置的决定性环节,船载GNSS动态PPP精度直接影响了最终的定位结果,将各项误差加以合理的约束和改正后,3个方向上的定位精度均能达到厘米级。
(2) 当采样时间间隔缩短或航迹点增多时,海上海下观测量增加,海底控制点三维坐标精度有明显提升,结合观测数据质量等因素,建议进行航线设计时,在保证海面海底空间几何图形强度的前提下,应适当增加航迹点和观测总数。
(3) 不同于航迹点,增加应答器个数不一定能改善定位结果,但若能保证应答器分布具有高度的对称性,且其构型有较合理的基线长度和较强的几何强度,则可以减弱声学测距误差,进而得到精确的定位坐标。
我国在海底大地控制网数据处理技术领域的研究还很少,受篇幅所限,本文对于实际确定海底控制点过程中的一些细节问题未展开详细讨论,如航线设计、声线修正、时间配准等方面。如何得到更有效、更利于我国实际应用的GNSS/声学定位系统及相应的数据处理策略,这也将是下一步需要进行深入研究的重点。
| [1] | 杨元喜, 徐天河, 薛树强. 我国海洋大地测量基准与海洋导航技术研究进展与展望[J]. 测绘学报, 2017, 46(1): 1–8. |
| [2] | SPIESS F N. Analysis of a Possible Sea Floor Strain Measur-ement System[J]. Marine Geodesy, 1985, 9(4): 385–398. |
| [3] | SPIESS F N, CHADWELL C D, HILDEBRAND J A, et al. Precise GPS/Acoustic Positioning of Seafloor Reference Points for Tectonic Studies[J]. Physics of the Earth and Planetary Interiors, 1998, 108(2): 101–112. DOI:10.1016/S0031-9201(98)00089-2 |
| [4] | YAMADA T, ANDO M, TADOKORO K, et al. Error Evaluation in Acoustic Positioning of a Single Transponder for Seafloor Crustal Deformation Measurements[J]. Earth Planets and Space, 2002, 54(9): 871–881. DOI:10.1186/BF03352435 |
| [5] | OSADA Y, FUJIMOTO H, MIURA S, et al. Estimation and Correction for the Effect of Sound Velocity Variation on GPS/Acoustic Seafloor Positioning:An Experiment off Hawaii Island[J]. Earth Planets & Space, 2003, 55(10): e17–e20. |
| [6] | FUJITA M, ISHIKAWA T, MOCHIZUKI M, et al. GPS/Acoustic Seafloor Geodetic Observation:Method of Data Analysis and Its Application[J]. Earth, Planets and Space, 2006, 58(3): 265–275. DOI:10.1186/BF03351923 |
| [7] | JR PURCELL G H, YOUNG L E, WOLF S K, et al. Accurate GPS Measurement of the Location and Orientation of a Floating Platform[J]. Marine Geodesy, 1990, 14(3-4): 225–264. DOI:10.1080/15210609009379665 |
| [8] | OBANA K, KATAO H, ANDO M. Seafloor Positioning System with GPS-acoustic Link for Crustal Dynamics Observation:A Preliminary Result from Experiments in the Sea[J]. Earth Planets Space, 2000, 52(6): 415–423. |
| [9] | TADOKORO K, ANDO M, IKUTA R, et al. Observation of Co-seismic Seafloor Crustal Deformation due to M7 Class Offshore Earthquakes[J]. Geophysical Research Letters, 2006, 332(23): 265–288. |
| [10] | SATO M, FUJITA M, MATSUMOTO Y, et al. Improvement of GPS/acoustic Seafloor Positioning Precision Through Controlling the Ship's Track Line[J]. Journal of Geodesy, 2013, 87(9): 825–842. DOI:10.1007/s00190-013-0649-9 |
| [11] | 朱俊江, 孙宗勋, 练数民, 等. 全球有缆海底观测网概述[J]. 热带海洋学报, 2017, 36(3): 20–33. |
| [12] | 许建平. 阿尔戈全球海洋观测大探秘[M]. 北京: 海洋出版社, 2002. |
| [13] | 李林阳, 吕志平, 崔阳. 海底大地测量控制网研究进展综述[J]. 测绘通报, 2018(1): 8–13. |
| [14] | GENG J, TEFERLE F N, MENG X, et al. Kinematic Precise Point Positioning at Remote Marine Platforms[J]. GPS Solutions, 2010, 14(4): 343–350. DOI:10.1007/s10291-009-0157-9 |
| [15] | 蔡艳辉.差分GPS水下定位系统集成关键技术研究[D].辽宁: 辽宁工程技术大学, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10147-2008050896.htm |
| [16] | HÉROUX P, KOUBA J. GPS Precise Point Positioning Using IGS Orbit Products[J]. Physics & Chemistry of the Earth Part A Solid Earth & Geodesy, 2001, 26(6-8): 573–578. |
| [17] | XU P, ANDO M, TADOKORO K. Precise, Three-dimensional Seafloor Geodetic Deformation Measurements Using Difference Techniques[J]. Earth Planets and Space, 2005, 57(9): 795–808. DOI:10.1186/BF03351859 |
| [18] | 汪德昭, 尚尔昌. 水声学[M]. 2版.北京: 科学出版社, 2013. |
| [19] | 方守川.海底电缆地震勘探导航定位关键技术研究及系统研制[D].武汉: 武汉大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10486-1015550338.htm |
| [20] | 赵建虎. 现代海洋测绘[M]. 武汉: 武汉大学出版社, 2008. |
| [21] | 高国青, 叶湘滨, 乔纯捷, 等. 水下声定位系统原理与误差分析[J]. 兵器装备工程学报, 2010, 31(6): 95–97. DOI:10.3969/j.issn.1006-0707.2010.06.030 |
| [22] | 施立涛.多传感器信息融合中的时间配准技术研究[D].长沙: 国防科学技术大学, 2010. http://cdmd.cnki.com.cn/Article/CDMD-90002-2010271398.htm |


