定位是机器人根据任务做出正确决策和路径选择的基础[1-2],如何设计基于多传感器的高精度和稳健性的跟踪定位模型显得尤为重要。传统的室外定位主要是卫星导航定位[3-5],室内定位算法主要有惯性导航法和视觉定位方法[6]。利用惯性传感器与图像传感器的互补性,可将视觉定位与惯性导航技术相融合,得到精度更高、稳健性更好的紧耦合定位技术。
单目视觉惯性紧耦合定位技术近年来发展迅速,由最初的基于卡尔曼滤波[7]的紧耦合方法逐渐发展到基于光束平差法(bundle adjustment,BA[8])优化和图优化的方法。Anastasios I.Mourikis于2007年提出了一个典型的基于扩展卡尔曼滤波的紧耦合模型MSCKF[9],从此开启了视觉惯性紧耦合的定位方法。MSCKF的跟踪模型是基本的视觉参考帧模型,在跟踪情况下没有使用IMU的先验数据,因此系统极易不收敛,导致定位精度较差。国外ORB_SLAM2[10]的作者Raul Mur-Artal于2017年提出了具有地图重用的视觉惯性单目SLAM技术[11],提出了一种简便的视觉惯性联合初始化方法,但该方法需要15 s左右的初始化时间,因此在初始化成功之前需要稳定的视觉前端基础,而ORB_SLAM在初始化期间采用的是简单的匀速跟踪模型,在相机剧烈运动时无法正确初始化,甚至跟踪失败。香港科大机器人研究所于2017年提出了VINS(visual-inertial system)[13],VINS视觉方面采用的是稀疏光流法进行跟踪定位,文中提出了一种稳健性的视觉惯性联合初始化过程和恢复过程,以及基于滑动窗口的紧耦合非线性优化方法,但是整个系统采用的是最基本的参考帧跟踪模型,无法克服复杂的运动环境。
综上所述,由于传统的单目视觉惯性定位跟踪模型都采用简单的参考帧模型和匀速模型,系统的定位结果易受剧烈运动和复杂环境影响,从而降低定位精度;而IMU先验数据可以有效克服剧烈运动等影响,因此设计一种面向单目视觉惯性紧耦合定位的IMU辅助跟踪模型具有重要的意义。
1 IMU辅助跟踪模型设计前文提到的匀速跟踪模型和传统的参考帧跟踪模型原理简单,但无法克服剧烈运动问题,因此本文重点提出一种IMU辅助跟踪模型。IMU辅助跟踪模型是结合单目匀速模型和IMU先验数据,为初始化阶段及初始化完成后提供一个稳健性的视觉前端,从而有效提高视觉惯性系统的整体性能。
1.1 IMU先验数据解算IMU可以输出加速度和角速度,对角速度进行积分可以获得IMU单元的相对旋转。
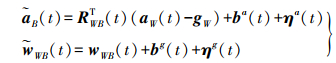 (1)
(1) 式中,B为IMU坐标系;W为世界坐标系;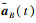
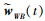
同时IMU的数据帧率一般远高于视觉,在视觉的k和k+1帧之间通常会有多组IMU数据,IMU预积分模型[14]即是计算视觉k和k+1帧之间的一组IMU积分值。式(2)为IMU运动模型
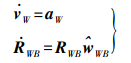 (2)
(2) 式中,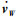
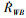
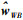
t+Δt时刻的运动状态可通过积分获得
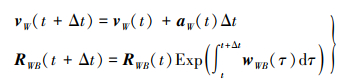 (3)
(3) 利用中值积分法,联立式(1)和式(3)可得
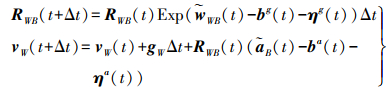 (4)
(4) 上式可以看出每次对t+Δt时刻的旋转计算都需要知道t时刻的旋转,因此当RWB(t)随时间变化后需要重新计算积分,这将导致计算量的增大。为了避免重复的状态传播计算,采用预积分的方式
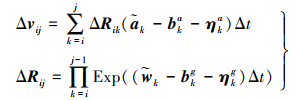 (5)
(5) 由预积分公式可以看出Δvij和ΔRij分别为i和j时刻之间的速度和旋转增量,数值受两个参数影响,分别为k时刻的偏置bkg、bka及噪声ηkg、ηka,并且关系复杂,因此需要分别考虑;RiT为i时刻旋转的转置;Rj为j时刻的旋转;vi、vj分别为i、j时刻的速度。首先假设偏置不变,仅讨论噪声的影响,接着再讨论偏置的影响,最后得到IMU先验值
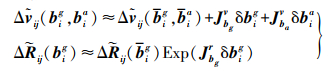 (6)
(6) 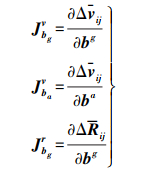 (7)
(7) 式中,JbgR为旋转对陀螺仪偏置的雅各比矩阵;Jbgv和Jbav为速度对偏置的雅各比矩阵;δbig和δbia为i和j时刻陀螺仪和加速度计偏置的变化量。
1.2 系统初始状态估计当系统处于初始化阶段时,由于系统速度、重力加速度和尺度无法获取,因此只能使用IMU旋转数据。
图 1为一般的匀速跟踪模型,假设有3个连续帧,F1、F2和F3之间的相对旋转分别为ΔR12和ΔR23,匀速跟踪模型是假设相邻帧之间的相对变换不变,即
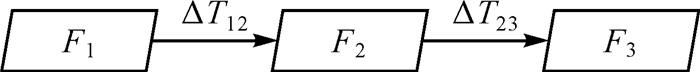
|
| 图 1 匀速跟踪模型 |
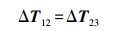 (8)
(8) F1与F2之间的相对变换
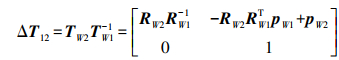 (9)
(9) 式中,RW1和RW2分别为F1和F2的旋转;pW1和pW2分别为F1和F2的位移;TW1和TW2分别为F1和F2的位姿。
因此F3的变换矩阵
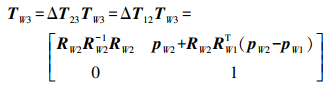 (10)
(10) 由旋转矩阵间的转换关系可知
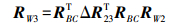 (11)
(11) 式中,RBC为相机和IMU之间的旋转外参;ΔR23为相机帧F2与相机帧F3之间的相对旋转,是由IMU先验数据提供;RW3为F3的旋转。
将旋转矩阵代入到变换矩阵模型中
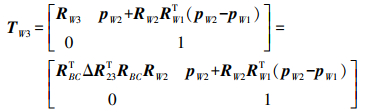 (12)
(12) 最终将改进的TW3作为初始值代入到优化模型中。
当系统完成初始化后,重力加速度和IMU速度可以准确地获得,因此在视觉优化前可以通过IMU获得整个系统的速度信息
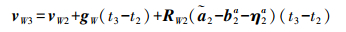 (13)
(13) 式中,t2和t3分别对应F2和F3的时刻;b2a和η2a为F2对应的加速度计偏置和加速度计噪声。最终将改进的TW3和vW3作为初始状态代入到优化模型中。
2 试验验证与结果分析本文中的算法验证基于视觉惯性ORB_SLAM2框架,数据采用的是EuRoC数据集,这些数据集都是由迷你飞行器对两个不同的房间和工业环境采集得到。数据集分为简单的、中等的和复杂的情况,所使用的视觉惯性器件为Ⅵ-Sensor双目惯性相机,其中相机的采样频率为20 Hz,IMU的采样频率为200 Hz,真实轨迹可由数据提供,试验只使用其左目相机,处理器使用的是内存为8 GB的Intel Core i7-7000笔记本。在整个试验中,将本方案分别和OKVIS双目[15]及ORB_SLAM2的双目作比较,本试验使用了两个数据集画图以验证试验效果,分别为V1_01_easy、MH_03_median。
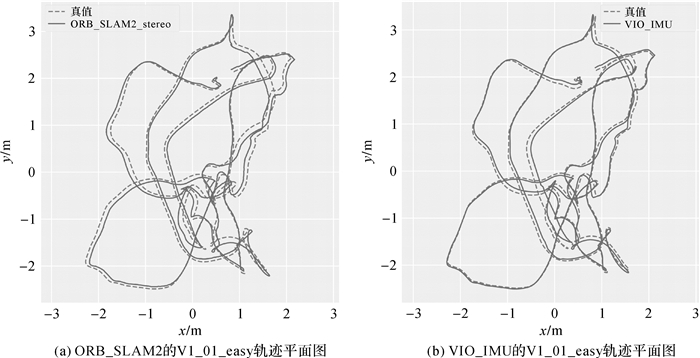
试验1采用V1_01_easy数据集,将本方案与ORB_SLAM2双目作比较,图 2(a)为ORB_SLAM2的V1_01_easy轨迹平面图,图 2(b)为VIO_IMU的V1_01_easy轨迹平面图,VIO_IMU为采用IMU辅助跟踪模型的定位结果图,其中ORB_SLAM2双目的均方根误差为0.087 m,VIO_IMU的均方根误差为0.065 m。由图 2(a)可以看出,VIO_IMU的定位轨迹与真实轨迹更为符合。图 3(a)给出了与ORB_SLAM2双目比较的V1_01_easy轨迹误差,图中可以明显看出VIO_IMU的定位误差在整体上要优于ORB_SLAM2双目的定位误差;表 1列出了定位误差的状态对比,可以看出,VIO_IMU定位误差的中误差、均方根误差、最小值、中位数、均小于ORB_SLAM2双目定位误差的相应结果。图 3右是定位误差的小提琴图,主要用来统计和分析数据的离散程度和分布密度,图中可以看出VIO_IMU误差的分布主要集中在0.025 m左右,而ORB_SLAM2双目主要集中在0.095 m附近,VIO_IMU误差的中位数和四分位数都优于ORB_SLAM2双目,上侧的离散情况二者基本相同,VIO_IMU误差的下侧离散值要优于ORB_SLAM2双目的误差。
|
| 图 2 |

|
| 图 3 |
| m | ||||
| 模型 | std | rmse | max | min |
| ORB_SLAM2双目 | 0.025 | 0.092 | 0.152 | 0.022 |
| VIO_IMU | 0.023 | 0.049 | 0.138 | 0.006 |
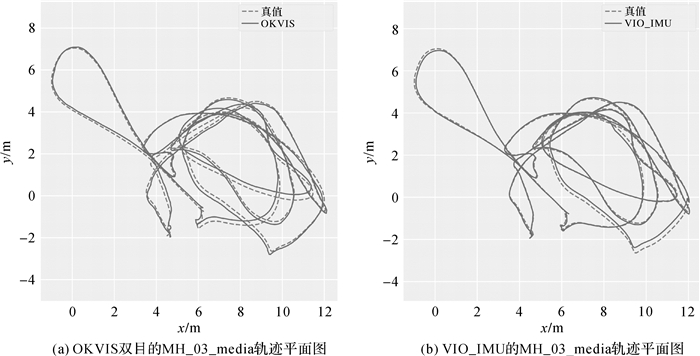
试验2采用MH_03_media数据集,将本方案与OKVIS双目作比较。由于本文的定位方案及OKVIS是由惯性器件来恢复整个系统的尺度信息,存在一定的尺度误差,而ORB_SLAM2可以直接由双目获得,对于中等尺度的MAV-MH数据集,ORB_SLAM2占绝对优势,因此MH_03_media数据集不考虑与ORB_SLAM2双目的比较。图 4(a)为OKVIS双目的MH_03_media轨迹平面图,图 4(b)为VIO_IMU的MH_03_media轨迹平面图,由图 4可知VIO_IMU和真实轨迹更为接近。表 2为视觉惯性辅助模型与OKVIS在EuRoC数据集下的定位均方根误差,由表 1可以看到本文提出的定位方案优于OKVIS的定位结果。
|
| 图 4 |
| m | ||||
| 模型 | V1_01 | V1_02 | V1_03 | MH_03 |
| OKVIS | 0.088 | 0.173 | 0.197 | 0.269 |
| VIO_IMU | 0.065 | 0.121 | 0.156 | 0.099 |
本文针对快速运动下单目视觉惯性定位跟踪失效的问题,提出了一种面向单目视觉惯性紧耦合定位的IMU辅助跟踪模型,主要利用IMU获得先验的运动状态作为整个系统的定位初值,代入到优化算法中,提升单目视觉惯性紧耦合定位下的稳健性。由于整个视觉惯性系统分为初始化状态和初始化完成状态,因此分别对不同阶段实现相应的跟踪方法,建立一个整体的IMU辅助跟踪模型。
通过对不同SLAM公开数据集进行试验验证,IMU辅助跟踪模型优于OKVIS双目定位模型,相比ORB_SLAM2双目的定位精度在小尺度范围内有较大的改善,说明本文的模型在单目视觉惯性定位中具有一定的研究意义。但本文的研究模型仍然存在不足之处,在初始位姿估计上只利用了IMU预积分提供的先验旋转和速度信息,当同时使用IMU预积分解算的位置数据时,定位结果出现较大误差。下一步将重点研究如何有效地将位置数据融合到初始位姿估计中,以提升单目视觉惯性紧耦合定位的精度和稳健性。
| [1] | 胡劲草. 室内自主式移动机器人定位方法研究[J]. 传感器世界, 2006, 20(11): 14–18. DOI:10.3969/j.issn.1006-883X.2006.11.003 |
| [2] | 李群明, 熊蓉, 褚健. 室内自主移动机器人定位方法研究综述[J]. 机器人, 2003, 25(6): 560–567. DOI:10.3321/j.issn:1002-0446.2003.06.017 |
| [3] | PAN S G, MENG X, WANG S L, et al. Ambiguity Resolution with Double Troposphere Parameter Restriction for Long Range Reference Stations in NRTK System[J]. Empire Survey Review, 2015, 47(345): 429–437. DOI:10.1179/1752270614Y.0000000144 |
| [4] | PAN S, MENG X, WANG G, et al. A New Approach for Optimising GNSS Positioning Performance in Harsh Observation Environments[J]. Journal of Navigation, 2014, 67(6): 1029–1048. DOI:10.1017/S0373463314000423 |
| [5] | 姜卫平. 卫星导航定位基准站网的发展现状、机遇与挑战[J]. 测绘学报, 2017, 46(10): 1379–1388. DOI:10.11947/j.AGCS.2017.20170424 |
| [6] | 王勇, 陈国良, 李晓园, 等. 一种相机标定辅助的单目视觉室内定位方法[J]. 测绘通报, 2018(2): 35–40. |
| [7] | JULIER S J, UHLMANN J K.A New Extension of the Kalman Filter to Nonlinear Systems[C]//Proceedings of SPIE.[S.l.]: SPIE, 1997. https://www.researchgate.net/publication/322276975_A_new_extension_of_the_Kalman_filter_to_nonlinear_systems |
| [8] | TRIGGS B, MCLAUCHLAN P F, HARTLEY R I, et al.Bundle Adjustment-A Modern Synthesis[C]//International Workshop on Vision Algorithms.Berlin: Springer, 1999: 298-372. https://link.springer.com/chapter/10.1007/3-540-44480-7_21 |
| [9] | MOURIKIS A I, ROUMELIOTIS S I.A Multi-state Constraint Kalman Filter for Vision-aided Inertial Navigation[C]//Proceedings 2007 IEEE International Conference on Robotics and Automation. Roma: IEEE, 2007: 3565-3572. https://www.researchgate.net/publication/224705670_A_Multi-State_Constraint_Kalman_Filter_for_Vision-Aided_Inertial_Navigation |
| [10] | MUR-ARTAL R, TARDÓS J D. Orb-slam2:An Open-source Slam System for Monocular, Stereo, and Rgb-d cameras[J]. IEEE Transactions on Robotics, 2017, 33(5): 1255–1262. DOI:10.1109/TRO.2017.2705103 |
| [11] | MUR-ARTAL R, TARDÓS J D. Visual-inertial Monocular SLAM with Map Reuse[J]. IEEE Robotics and Automation Letters, 2017, 2(2): 796–803. DOI:10.1109/LRA.2017.2653359 |
| [12] | LEE D, KIM H, MYUNG H. 2D Image Feature-Based Real-Time RGB-D 3D SLAM[J]. Springer Berlin Heidelberg, 2013, 208: 485–492. |
| [13] | QIN T, LI P, SHEN S. Vins-mono:A Robust and Versatile Monocular Visual-inertial State Estimator[J]. ArXiv Preprint, 2017, 8: 210–235. |
| [14] | FORSTER C, CARLONE L, DELLAERT F, et al. On-manifold Preintegration for Real-time Visual-inertial Odometry[J]. IEEE Transactions on Robotics, 2017, 33(1): 1–21. |
| [15] | LEUTENEGGER S, LYNEN S, BOSSE M, et al. Keyframe-based Visual-inertial Odometry Using Nonlinear Optimization[J]. The International Journal of Robotics Research, 2015, 34(3): 314–334. |


