InSAR技术是近年来测量技术的研究热点,具有全天候、周期性短、不受气候条件影响的特点[1],而DInSAR技术是InSAR技术的扩展,旨在监测地表的形变,其精度可达到厘米甚至毫米级。DInSAR的关键处理步骤包括影像配准、干涉图生成、形变相位分离、相位解缠、地理编码和投影变换等[2],而干涉图生成和相位解缠方法一直是DInSAR技术的研究热点和难点,本文主要研究差分干涉图的噪声去除问题。对于干涉图去噪方法的研究也已经发展了很多年,取得了许多成果。1998年,Goldstein提出Goldstein滤波算法,也成为了经典干涉图滤波方法[3];2000年,万朋等将Wiener滤波运用到SAR图像地物边界提取[4];2001年,郭宏雁等分析了自适应中值滤波在SAR相干斑噪声抑制的效果[5];2007年,罗海滨针对单一滤波方法对InSAR干涉图去噪的不足,提出了两种滤波相结合的综合滤波方案,引发了InSAR干涉图滤波方法的新思考[6];2012年,刘长安等采用多尺度多方向滤波窗口, 自适应地选择窗口进行加权中值滤波处理[7];2013年,余景波等提出采用综合滤波方法对InSAR干涉图去噪进行了试验分析,结果表明综合滤波去噪方法应用于InSAR干涉图是可行的[8];2013年,贾凌春等设计了一种自适应Gabor干涉图滤波器[9];2014年,黄长军等提出一种基于EDM-自适应滤波干涉图去噪方法[10];2015年,李泓宇等改进了复值马尔可夫随机场模型干涉图滤波算法[11];2015年,汪洋等利用分块局部的思想,改进了维纳滤波算法,并应用于干涉相位图中取得很好的效果[12];2016年,赵文胜等在Goldstein频域滤波之上,提出了一种基于第二类统计Goldstein自适应滤波算法[13];2017年,蒋锐等利用多基线InSAR的数据特点,提出了基于信号子空间估计的多基线InSAR干涉图相位图滤波方法[14];2017年,刘晓君等针对SAR影像噪声特性提出一种改进的Ration算子与Canny算子相组合的方法,提高了SAR影像的边缘检测率和定位精度[15]。
Non-local Meas滤波算法已广泛用于各种图像去噪领域,如医学、电子信号学等,其算法对于图像去噪的中心思想是利用图像的区域相似性实现对于噪声密度较高的区域进行去噪和修复,但传统的Non-local Meas算法在平滑参数的选择上具有固定性,而InSAR干涉图像上噪声具有不均衡的特性,很难找到一个固定的平滑参数对整幅干涉图进行滤波处理后取得良好的去噪效果,针对这个问题,本文提出一种基于干涉图相干系数自适应的Non-local Means算法。该算法既兼顾了传统Non-local Means滤波算法优点的同时,又能够适应InSAR干涉图上噪声不均衡的特性,保留了InSAR干涉图中更多的条纹信息和细节特征,为正确解缠提供了有利条件。
1 算法原理及实现 1.1 非局部化(Non-local Means)滤波算法原理非局部化图像修复算法是近年来新兴的图像处理算法,其原理是通过寻找整幅图像中与待恢复区域相似的块,再将找出的所有相似块通过某种相似性准则(如K均值聚类)进行聚类后联合滤波[16],从而减少图像噪声。而对于图像相似性的计算,可以通过比较一个窗口内的各个像素值来得到。Non-local Means算法公式为
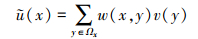 (1)
(1) 式中,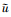
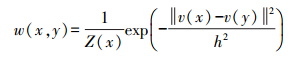 (2)
(2) 其中
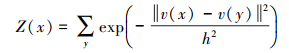 (3)
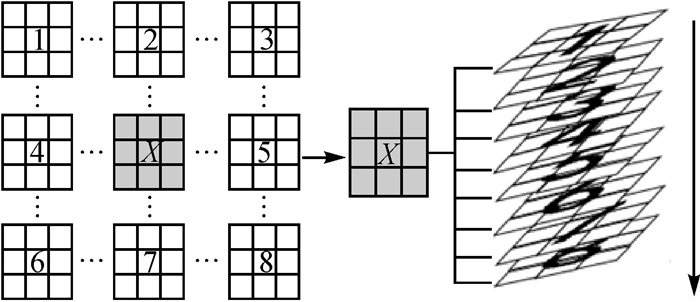
(3) Z(x)表示归一化系数,h为平滑参数。图像块之间的相似性由欧氏距离决定,从式(2)中可以看出,欧氏距离越大,该算法去噪能力对平滑参数的选择依赖性越高。Non-local Means算法的理论思想是,在遍历整幅图像像素后判定像素间的相似度,但是在实际实现过程中,考虑算法的效率,设定一个搜索窗口和一个邻域窗口,缩小需要参与相似度判定的像素范围,提高算法的效率,邻域窗口在搜索窗口内进行滑动比较,根据邻域间的相似度计算像素的权值。如图 1所示,x为固定的邻域窗口,1、2、3、4、5、6、7、8为滑动窗口依次滑过形成的邻域窗口,通过比较x与邻域窗口的相似度,确定邻域窗口图像块的权值。
|
| 图 1 NL-Means算法示意图 |
由于滤波平滑参数的固定性,传统Non-local Means滤波算法无法适应InSAR干涉图噪声分布不均衡的特性,当平滑参数设置较大时,干涉图噪声密度低的区域细节纹理丢失,反之,干涉图噪声高的区域则去噪效果不明显,最终导致整幅干涉图质量的下降。针对这个问题,本文提出了基于相干系数的自适应Non-local Means算法。相干系数最早由Prati等于1993年提出,它是干涉图像对相位稳定性的衡量标准。假设C1、C2分别为同一地面分辨率单元在两幅SAR影像上的复数值,则有
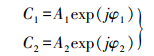 (4)
(4) 该分辨率单元的相位差为
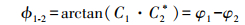 (5)
(5) 式中,Ai、φi分别为复数Ci的灰度和相位值,i=1, 2,则该分辨单元的相干系数为
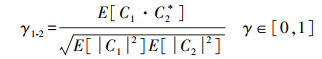 (6)
(6) 式中,C2*为C2的共轭复数;|C1|2、|C2|2为功率影像;E[ ]为整体平均值。当γ为0时,表示两幅影像完全失相干;当γ为1时,表示两幅图像相同。然而在实际观测中,每次干涉成像像元都不在同一时空位置,因此在实际计算中,将一定区域内的观测相位认为是平稳随机的过程,则可以利用像元周边区域为M×N的整体相干系数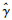
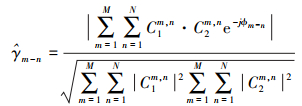 (7)
(7) 当相干值较小时,则认为区域噪声较大,应使用较大的平滑参数;当相干值较大时,则认为该区域噪声较小,应使用较小的平滑参数。根据这一关系,本文设计的线性自适应平滑参数模型为
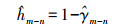 (8)
(8) 根据此模型得到的自适应平滑参数选择Non-local Means算法的搜索窗口和邻域窗口大小。马晓双[17]等在研究非局部加权最小均方误差算法在极化SAR方向的应用时发现,当搜索窗口的选择达到15×15之后,去噪效果的提升就会很小。本文在进行试验时,得到同样的试验结论,因此本文选择15×15的搜索窗口。而邻域窗口的大小对于去噪敏感度较高,邻域窗口越大,去噪效果越显著,但图像细节丢失度越高;反之,邻域窗口较小时,去噪效果较弱,但能更好地保持图像的细节信息[18]。基于此,本文依据式(7)得到的平滑参数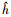
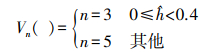 (9)
(9) 式中,Vn( )表示大小为n×n的邻域窗口。当平滑参数较小时,认为此区域噪声较小,则选择3×3的邻域窗口,保留InSAR干涉图更多的细节信息;当平滑参数较大时,则认为该区域噪声较大,选择去噪效果更好的5×5的邻域窗口进行滤波,而对去噪后相位值的选择则为与相位值相似高斯邻域的相位值的平均。综上所述,本文提出的自适应Non-local Means算法InSAR干涉图去噪步骤流程如图 2所示。
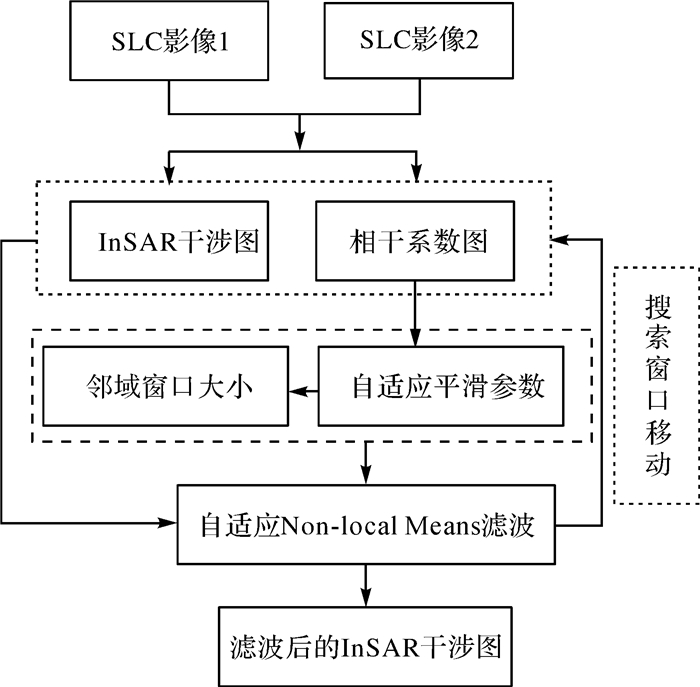
|
| 图 2 自适应Non-local Means算法去除干涉图噪声流程 |
本文采用的成像数据为台湾某地区地震前后的两幅SLC影像,利用ENVI中的SARscape处理功能,获得了去平后的干涉图,截取了1200×1200分辨率单元的区域图像,如图 3所示,其中A线为后续分析的剖断面位置示意图。从图中大致可以看出相位的周期性变化,但是由于存在严重噪声,原始干涉图纹理及细节信息被覆盖,很难解译出连续、正确的相位信息,也对相位解缠造成了困难。本文利用Matlab平台设计了传统Non-local Means滤波、Goldstein滤波、自适应中值滤波和本文提出的自适Non-local Means滤波并提取了相干系数矩阵(如图 4(e)所示),前3种滤波分别对原始干涉图进行滤波处理,改进滤波算法结合原始干涉图以及相干系数矩阵进行同步分块操作,并利用式(8)、式(9)得到原始干涉图分块的大小及相应的平滑参数,结果如图 4所示。

|
| 图 3 原始干涉图像 |

|
| 图 4 4种滤波方法结果以及相干系数图 |
从直观上对4种滤波结果进行对比可以看出,自适应中值滤波的效果最差,这是由于原始干涉图上噪声密度过大,而自适应中值滤波无法在噪声密度过大的情况下保持原有的滤波效果,导致图像碎片化严重;传统Non-local Means算法优于自适应中值滤波,特别是在干涉图中心,噪声密度最大处;传统Non-local Means算法去噪效果要优于Goldstein滤波,这是由Non-local Means算法原理决定的,在图像噪声集中的区域,Non-local Means算法利用图像的冗余信息,将每个像素与周围区域的所有像素进行对比,获得更加准确的权值,从而达到更好的去噪效果。但传统Non-local Means算法由于滤波参数选择的固定性导致在边缘保持能力及图像清晰度方面不及Glodstein滤波。从去噪后的干涉图形这一宏观角度进行对比分析,改进的滤波算法具有强于其他3种滤波的去噪能力。
图 5为4种滤波图像局部横断面信息,横断面选择从地震边缘穿过地震发生中心噪声最密集的区域,能代表性地体现滤波的去噪能力和平滑效果,如图 2中的A线所示。根据剖断面的选择,理论上干涉图的相位变化应当从中垂线处大致呈对称变化,根据实际所得的剖断面信息发现,自适应中值滤波及Goldstein滤波对称变化不明显,但Goldstein滤波与自适应中值滤波相比,处理的图像含有更多的毛刺,这是由于自适应中值滤波虽然将含噪声的干涉图进行碎片化,但其相位纹理变化特征明显,而Goldstein滤波在噪声密度大的中心区域去噪能力迅速下降,导致剖断面图像的不平滑;传统Non-local Means与改进的自适应Non-local Means滤波剖断面图像随相位的周期性变化明显,但传统Non-local Means滤波后的剖断面含有较多毛刺且不光滑,而改进的Non-local Means算法剖断面更加平滑,且毛刺较少,证明了改进的Non-local Means算法在保持条纹边缘和相位细节的同时能很好地抑制斑点噪声。
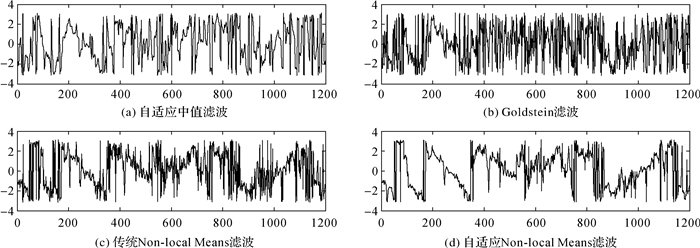
|
| 图 5 4种滤波A线剖面图 |
为了能客观评价改进的Non-local Means算法在InSAR干涉图去噪的能力,选择标准差、PSNR及残差点个数比较4种滤波的去噪能力。标准差是反映样本的离散程度,一种相位边缘保持能力好的滤波算法,应该使滤波后标准差的变化不大,最好能有微小的增加[19];PSNR体现图像的抗噪能力,残差点个数反映了干涉图像受噪声污染的程度,也是相位能够正确解缠的重要指标,4种滤波后的干涉图以及原始干涉图标准差和残差点个数见表 1。从表 1中可以看出,4种滤波结果的标准差与原始干涉图相比,变化幅度较小,基本满足滤波指标的要求,PSNR值方面,改进的Non-local Means算法高于其他3种滤波方法,反映出改进算法具有更高的峰值信噪比,而残差点个数减少程度变化较大,改进的Non-local Means滤波算法得到的结果相对于原始干涉图减少了92.5%的残差点,远低于其他3种滤波处理后的残差点个数。
| 干涉图 | 标准差/rad | PSNR | 残差点/个 |
| 原始干涉图 | 1.818 4 | — | 377 445 |
| 自适应中值滤波 | 1.809 6 | 40.250 5 | 54 202 |
| Goldstein滤波 | 1.815 1 | 42.030 4 | 126 535 |
| 传统Non-local Means滤波 | 1.838 9 | 41.159 2 | 97 234 |
| 改进的Non-local Means滤波 | 1.840 6 | 43.698 5 | 28 604 |
Non-local Meas算法充分利用图像的冗余信息,在图像去噪方面其算法原理具有很强的优势性。针对InSAR干涉图噪声特性,本文提出了基于InSAR干涉图相干系数滤波参数自适应的Non-local Means算法,并利用实际算例证明了改进的Non-local Means算法从目视解译到客观指标评价,都表现出优于其他3种滤波方法的去噪能力以及纹理和边缘信息保持能力,说明了改进的Non-local Means算法是一种有效的InSAR干涉图滤波方法。
| [1] | PARRILLI S, PODERICO M, ANGELINO C. A Nonlocal SAR Image Denoising Algorithm Based on LLMMSE Wavelet Shrinkage[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(2): 606–616. DOI:10.1109/TGRS.2011.2161586 |
| [2] | ZHANG W G, ZHANG Q, YANG C S. Improved Bilateral Filtering for SAR Image Despeckling[J]. Electronic Letters, 2011, 47(17): 286–288. |
| [3] | GOLDSTEIN R M, WERNER C L. Radar Interferogram Filtering for Geophysical Applications[J]. Geophysical Research Letters, 1998, 25(21): 4035–4038. DOI:10.1029/1998GL900033 |
| [4] | 万朋, 王建国, 赵志钦, 等. SAR图像弱反射地物边缘提取方法[J]. 信号处理, 2000, 16(4): 317–323. DOI:10.3969/j.issn.1003-0530.2000.04.006 |
| [5] | 郭宏雁, 王建国, 黄顺吉. 一种新的SAR相干斑抑制方法[J]. 系统工程与电子技术, 2001, 23(11): 38–39. DOI:10.3321/j.issn:1001-506X.2001.11.013 |
| [6] | 罗海滨, 何秀凤. InSAR相位干涉图滤波方法研究[J]. 测绘通报, 2007(5): 55–57. DOI:10.3969/j.issn.0494-0911.2007.05.017 |
| [7] | 刘长安, 王志勇. 基于多尺度多方向的InSAR自适应相位滤波[J]. 遥感信息, 2012, 27(3): 11–14. DOI:10.3969/j.issn.1000-3177.2012.03.002 |
| [8] | 余景波, 刘国林, 曹振坦, 等. 综合滤波InSAR干涉图去噪实验分析[J]. 测绘科学, 2013, 38(5): 129–132. |
| [9] | 贾凌春, 唐锁夫, 罗彦龙, 等. 基于Gabor滤波器的干涉相位图滤波算法[J]. 四川兵工学报, 2013, 34(12): 123–127. DOI:10.11809/scbgxb2013.12.034 |
| [10] | 黄长军, 郭际明, 喻小东, 等. 干涉图EMD-自适应滤波去噪法[J]. 测绘学报, 2013, 42(5): 707–714. |
| [11] | 李泓宇, 宋红军, 王辉, 等. 质量图指导的改进的基于CMRF模型的自适应InSAR相位滤波[J]. 科学技术与工程, 2015, 15(25): 55–60. DOI:10.3969/j.issn.1671-1815.2015.25.010 |
| [12] | 汪洋, 黄海风, 董臻, 等. 改进分块局部最佳维纳滤波算法的干涉相位滤波[J]. 国防科技大学学报, 2015, 37(4): 99–105. |
| [13] | 赵文胜, 蒋弥, 何秀凤. 干涉图像第二类统计Goldstein自适应滤波方法[J]. 测绘学报, 2016, 45(10): 1200–1209. DOI:10.11947/j.AGCS.2016.20150457 |
| [14] | 蒋锐, 龚清勇, 朱岱寅, 等. 基于信号子空间估计的多基线InSAR干涉相位图滤波方法[J]. 数据采集与处理, 2017, 32(2): 375–381. |
| [15] | 刘晓君, 韩芳, 赵磊. 一种改进的SAR影像边缘检测方法[J]. 测绘通报, 2017(9): 56–59. |
| [16] | 乔子良, 杜慧敏. 基于K均值聚类NL_MEANS算法的超声图像去噪[J]. 计算机工程与设计, 2014, 35(3): 939–942. DOI:10.3969/j.issn.1000-7024.2014.03.039 |
| [17] | 马晓双, 沈焕锋, 杨杰, 等. 极化SAR相干斑抑制的非局部加权最小均方误差滤波算法[J]. 中国图象图形学报, 2015, 20(1): 140–150. |
| [18] | CHEN J, CHEN Y, AN W, et al. Nonlocal Filtering for Polarimetric SAR Data:A Pretest Approach[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(5): 1744–1754. DOI:10.1109/TGRS.2010.2087763 |
| [19] | 何敏, 何秀凤. 基于小波域HMT模型InSAR干涉图噪声滤波研究[J]. 遥感技术与应用, 2007, 22(4): 531–535. DOI:10.3969/j.issn.1004-0323.2007.04.009 |


