为实现基于点云数据的工业构件加工质量检测,需利用三维激光扫描仪扫描工业构件,得到的点云数据有着很高的精度,但也包含大量的冗余点。这些冗余点会给计算机建模、传输,以及构件的快速检测带来阻碍。工业构件的几何特征是对其进行检测的基础,在保证被测构件几何特征的前提下,对点云数据进行精简,可以减少存储空间,提高计算速度,突出建模特征,对曲面重构的速度和效率可以产生重要的影响[1, 2]。
国内外学者在点云数据精简方面作了很多研究,比较有代表性的有3类:第一类,最初由Martin[3]提出的基于均匀格网划分的散乱点云数据精简方法,但该方法不适用于非均匀分布的点云;第二类,基于空间包围盒[4-5]的散乱点云数据精简方法,空间包围盒法与均匀格网划分思路基本一致,只是在选点上进行了改进,这种方法不适用于曲率变化较大且形状复杂的数据点云, 可能导致某些过渡区域的重要数据点的丢失;第三类,基于曲率采样的散乱点云数据精简方法[6-8],利用不同的拟合法求解局部曲率,再根据曲率偏差对点云进行精简,曲率能够很好地反映点云的特征,但曲率的计算复杂,影响精简速度。
本文针对工业构件提出一种基于曲面变化的点云精简算法。在建立点云空间邻域关系后,通过计算点的曲面变化将点云分成特征不同的3个区域,对不同点区域设定权值,利用点的曲面变化定义近似特征点阈值,将曲面变化大于该值的点保留,小于该值的点进一步按照属于不同的特征区域计算其精简比率,由精简比率定义距离阈值,完成精简。
1 基于曲面变化的工业构件点云数据精简 1.1 散乱点云空间拓扑关系确定手持扫描仪获取的点云为散乱点云,每个数据点只具有三维坐标值的信息,没有明确的空间邻域信息,不利于邻域数据点的搜索,而邻域数据点的搜索速度正是影响散乱数据处理和曲面重构效率的主要因素之一,因此必须建立数据点间的空间拓扑关系以搜索每个点的K邻近。常用的空间栅格法的思路是,通过三维散乱点云的空间划分确定散乱点云的空间位置,将点云数据按X、Y、Z划分成M、N、T个部分。散乱点云空间栅格化后,不但可以求出每个点所在的栅格位置,而且可以确定每个栅格中点云的个数。
1.2 点的曲面变化Paulyt[9]等提出了曲面变化(surface variation)概念来衡量曲面的弯曲程度,记为δk,它可以直接从散乱点云数据中计算出来。曲面变化能够近似表示该点附近的曲面变化程度和特征明显度,处于特征明显地段的点的曲面变化率大,相反处于特征不明显、不尖锐的地方的点的曲面变化率小。在表达曲面几何特征方面曲面变化非常接近于曲率,且不需要进行复杂的曲率计算。
设P点为散乱点云中一点, M3×3为P及其K邻近点所构成的协方差矩阵,P点的曲面变化δk可以由式(3)求出。
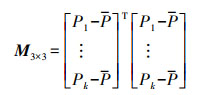 (1)
(1) 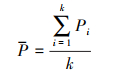 (2)
(2) 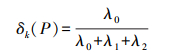 (3)
(3) 式中,P1、P2、…、Pk为P的K邻近点;λ0、λ1、λ2为协方差矩阵M3×3的特征值,且λ0为最小特征值。实际上,特征值λ0、λ1、λ2分别表示了点云数据在3个主方向的变化程度。由于M3×3是对称矩阵,因此λ0、λ1、λ2都为正值,那么δk(P)的取值范围就是0, 1/3。当P及P的K邻近点各向均匀分布时, δk(P)=0。因此,δk(P)的取值反映了曲面在P点沿其法向量方向离开切平面的程度。
1.3 点集划分将所有点按照各自的曲面变化值δk分成3个集合Qi(i=1, 2, 3),分别为平面邻域类型、次特征邻域类型和特征邻域类型,并使每个区间的点的数目相等。对于曲面变化最小的平面邻域类型点集Q1,其特征最弱,点对模型的影响程度也最低;曲面变化次大的次特征邻域类型点集Q2,区域特征稍强,点的影响程度也稍强;曲面变化最大的特征邻域类型点集Q3,区域特征最明显,相对属于特征部分,点的影响程度也最强。
1.4 点云精简策略所有点云精简的基本法则在于特征明显处的点尽量保留,精简率小,而在特征不明显处相对可以进行多精简。定义近似特征点阈值如下
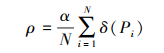 (4)
(4) 式中,δ(Pi)为点Pi的曲面变化;N为点云中的点数;α为调节因子,根据点云表面曲面变化情况依经验设置。如果点云中的点的曲面变化大于ρ,认为该点为近似特征点,则该点不被删除保留下来。
对于曲面变化小于特征点阈值ρ的点,暂时标记为不保留,按照其δ(Pi)进行降序排列,从大到小逐点在其K邻域内判断如何精简。按上文所述,将所有的点按照曲面变化的值划分为3个集合,3个集合按照其中的点对于点云整体形状的影响程度从小到大排列,分别为Q1、Q2、Q3。定义精简比率如下
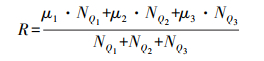 (5)
(5) 式中,NQ1、NQ2、NQ3分别代表该点K邻域中分别属于Q1、Q2、Q3集合的点的数目;μ1、μ2、μ3分别为3类点集的权重系数,权重系数可根据精简情况自行调整,按照点集中点的影响力程度设置,在此分别设为0.9、0.6、0.3。计算得出的点的R值的大小能够更好地反映单个点邻域特征明显的点所占权值的高低情况。如果周围特征明显,那么该点附近的精简率就要低一些。再根据该点的精简比率R计算出该点的精简距离阈值
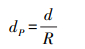 (6)
(6) 式中,d为初始设定距离,对于不同的点云模型,为求得更好的效果,一般先根据点云的密度估算一个d,然后再进行调整。遍历点P的K邻域,计算每点与P点的距离dPi(i=1, 2, …, K),当dPi<dP且δ(Pi)<ε时,其中阈值ε与近似特征点阈值ρ有关,可取ε=0.3ρ,则精简去除该点,直至精简结束。
2 精简边界保护边界对于工业构件点云数据的后续处理特别是曲面的重构十分重要,利用曲率变化作为准则精简时,尽管可以在保证几何特征的前提下精简,但被测物体的边界还是会受到影响。
周煜[10]等提出的一种基于立方体的边界保护方法,结合曲面变化进行改进。在空间栅格划分后,对立方体空间进行二值化处理,用函数g(x, y, z)表示立方体空间是否包含数据点,若g(x, y, z)=0,则表示立方体空间内不包含有数据点,定义为空体;若g(x, y, z)=1,则表示立方体空间内包含有数据点,定义为实体。
设δ表示立方体空间内所有数据点的曲面变化的平均值,定义函数
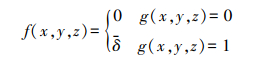 (7)
(7) 在空间栅格化后的空间中,每个立方体G存在26个相邻立方体。用(x, y, z)表示G,(i, j, k)表示G拓扑方向,则G的26个邻接立方体可由(x+i, y+j, z+j)表示,其中i∈[-1, 1], j∈[-1, 1], k∈[-1, 1],且(i, j, k)不同时为0。构造函数QΔ(x, y, z)表示G的26个邻接立方体中实体的数目,即
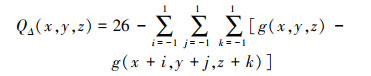 (8)
(8) 如果QΔ(x, y, z)=0,说明G没有实体与其相邻,称G为孤立立方体。基于曲面变化的差值构建G与26个邻接立方体的曲面变化差函数UΔ
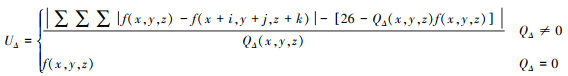 (9)
(9) 由式(9)可以看出,G的26个邻接立方体:实体数目越少,则QΔ越少,此时UΔ值显著增大;G与相邻立方体的曲面变化差越大,式(9)中的分子越大,则UΔ值增大。因此,可根据曲面变化差UΔ值判别G是否为边界立方体。设定边界特征参数σ,比较曲面变化差与边界特征参数,若UΔ>σ,则认为G为边界立方体,精简时对其数据点予以保护。
3 试验与分析利用本文提出的基于曲面变化的点云精简方法进行点试验。试验1数据为斯坦福大学三维扫描库中著名的bunny点云数据,试验2数据为利用手持三维激光扫描仪扫描的盒子点云数据,试验3数据为手持三维激光扫描仪扫描的工业零件点云数据。对上述数据采用基于曲率的精简方法处理,再与本文的精简算法从精简的简度、速度及精度3方面进行比较[11]。
为保证本文算法和基于曲率精简的精简率大致在相同的前提下进行3组试验数据分析,精简前后数据的点的个数及精简率统计见表 1,精简结果如图 1-图 11所示,其中图 7和图 11是进行了边界保护的精简结果。

|
| 图 1 bunny点云 |

|
| 图 2 基于曲率精简后bunny点云 |

|
| 图 3 本文方法精简后bunny点云 |

|
| 图 4 盒子点云 |

|
| 图 5 基于曲率精简后盒子点云 |
|
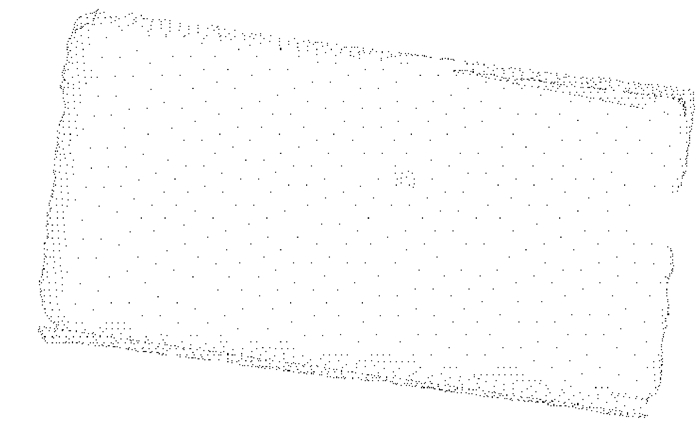
| 图 6 本方方法精简后盒子点云(边界未保护) |

|
| 图 7 本方方法精简后盒子点云(边界保护) |
|
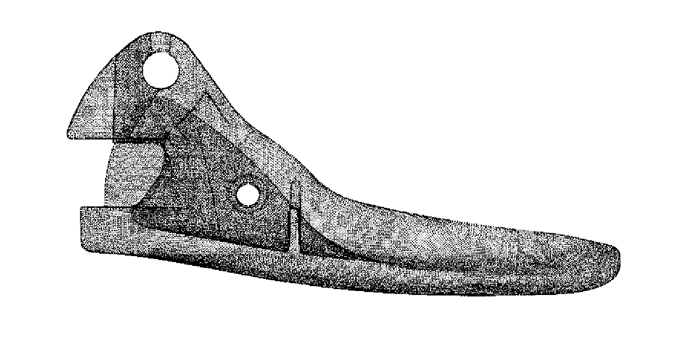
| 图 8 工业零件点云 |

|
| 图 9 基于曲率精简后零件点云工业零件点云 |
|
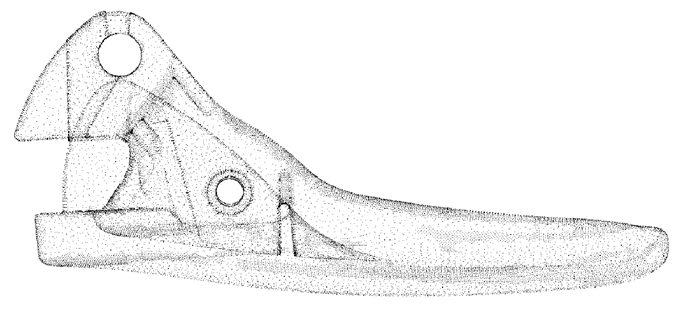
| 图 10 本文算法精简后工业零件点云(未加边界保护) |
|
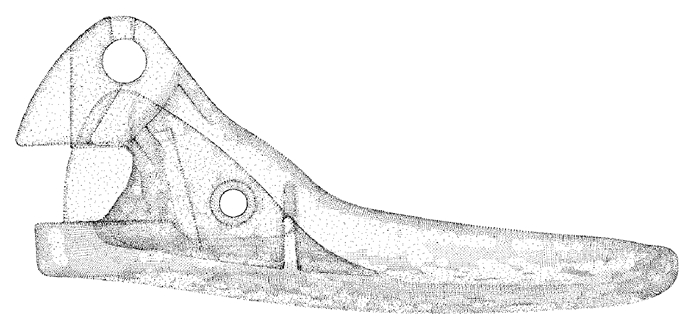
| 图 11 本文算法精简后工业零件点云(加边界保护) |
| 点云数据 | 本文方法 | 基于曲率精简方法 | |||||
| 精简前点数/个 | 精简后点数/个 | 精简率/(%) | 精简前点数/个 | 精简后点数/个 | 精简率/(%) | ||
| 盒子 | 9648 | 2151 | 22 | 9648 | 2284 | 24 | |
| 零件 | 100 040 | 30 850 | 30 | 100 040 | 30 411 | 30 | |
| bunny | 17 418 | 8997 | 52 | 17 418 | 8695 | 50 | |
由图可知,试验1 bunny点云因为表面曲率变化相对复杂,基于曲率的精简方法处理的结果并没有突出特征,而本文方法在特征处保留的点比较多;试验2精简后在盒子平面处的点云,本文方法处理的点均匀且达到了精简的目的;试验3零件精简后的结果相近,但本文方法相对基于曲率的精简方法处理的结果在特征处保证了更多的点,可保证后续建模的需要。综上可知,在精简率相同的前提下,本文方法可以达到与基于曲率的精简方法相似的处理效果,并且更好地保护了特征。
统计本文精简方法和基于曲率的精简方法处理3个点云数据的时间见表 2。由表 2可知, 本文的方法相对于基于曲率的精简方法精简速度有很大提高。
| ms | ||
| 点云数据 | 本文方法 | 基于曲率精简方法 |
| bunny | 10 655 | 20 753 |
| 盒子 | 6102 | 14 158 |
| 零件 | 68 640 | 118 462 |
精简的最终目的是在保证精度的前提下提高简度与速度。笔者利用体积法[12]对本文方法的精简精度进行分析评价。选取工业零件点云数据和本文基于曲面变化精简并加入边界保护处理后的点云数据, 以及基于曲率精简后的零件点云数据进行评价,统计数据见表 3。从表中可知,在精简率达到30%的情况下,本文方法与基于曲率的方法处理后的点云与原点云体积变化率只有0.06%,说明精简后体积损失很小,且达到了精简效果。
| 数据 | 点云数/个 | 精简率/(%) | 体积/mm3 | 体积变化/(%) |
| 零件点云 | 100 040 | 15 820.48 | ||
| 本发明方法精简后(边界保护) | 30 850 | 30 | 15 810.79 | 0.06 |
| 基于曲率方法精简后 | 30 411 | 15 792.14 |
本文针对工业构件提出了基于曲面变化的点云精简算法,通过计算点的曲面变化将点云分成特征不同的3个区域,对不同点区域设定权值,利用点的曲面变化定义近似特征点阈值,将小于阈值的点按照属于不同的特征区域计算其精简比率,由精简比率定义距离阈值完成精简。试验结果表明,在近似的精简比率前提下,本文的点云精简方法在精简精度上可以达到与基于曲率精简方法相同的效果,且计算速度更快,更好地保持了几何特征;加入边界保护处理后,精简对边界影响也比较小,可以满足后续建模要求。在表达曲面几何特征方面曲面变化非常接近于曲率,因此该方法能够尽可能地保留区域特征明显的点,且不需要进行复杂的曲率计算,精简效率比较高。
| [1] | RUWEN S, SEBASTIAN M, REINHARD K. Fast Vector Quantization for Efficient Rendering of Compressed Point Clouds[J]. Computers & Graphics, 2008(32): 246–259. |
| [2] | LEE K, WOO H, SUK T. Point Data Reduction Using 3D Grids[J]. The International Journal of Advanced Manufacturing Technology, 2001, 18(3): 201–210. DOI:10.1007/s001700170075 |
| [3] | MARTIN R R, STROUD I A, MARSHALL A D. Data Reduction for Reverse Engineering[J]. The Mathernatics of Surfaces, 1997, 10(1): 85–100. |
| [4] | FILIP D, MAGEDSON R, MARKOT R. Surface Algorithms Using Bounds on Derivatives[J]. Computer Aided Geometric Design, 1986, 3(2): 295–311. |
| [5] | 洪军, 丁玉成, 曹亮, 等. 逆向工程中的测量数据精简技术研究[J]. 西安交通大学学报, 2004, 38(7): 661–664. DOI:10.3321/j.issn:0253-987X.2004.07.001 |
| [6] | 周绿, 林亨, 钟约先, 等. 曲面重构中测量点云精简方法的研究[J]. 中国制造业信息化, 2004, 33(5): 102–104. DOI:10.3969/j.issn.1672-1616.2004.05.036 |
| [7] | 张丽艳, 周儒荣, 蔡炜斌, 等. 海量测量数据简化技术研究[J]. 计算机辅助设计与图形学学报, 2001, 13(11): 1019–1023. DOI:10.3321/j.issn:1003-9775.2001.11.011 |
| [8] | DYN N, FLOATER M S, ISKE A. Adaptive Thinning for Bivariate Scattered Data[J]. Journal of Computational and Applied Mathematics, 2002, 145(2): 505–517. DOI:10.1016/S0377-0427(02)00352-7 |
| [9] | PAULY M, GROSS M, KOBBELT L P.Efficient Simplifi-cation of Point-sampled Surfaces[C]//Proceedings of the Conference on Visualization 2002.[S.l.]: IEEE, 2002. https://dl.acm.org/citation.cfm?id=602123 |
| [10] | 周煜, 张万兵, 杜发荣, 等. 散乱点云数据的曲率精简算法[J]. 北京理工大学学报, 2010, 30(7): 785–789. |
| [11] | 赵伟玲, 谢雪冬, 程俊廷, 等. 保留边界特征的点云简化算法[J]. 黑龙江科技学院学报, 2013, 23(1): 83–88. DOI:10.3969/j.issn.1671-0118.2013.01.018 |
| [12] | FLEISHMAN S, DRORI I, COHENOR D. Bilateral Mesh Denoising[J]. ACM Transactions on Graphics, 2003, 22(3): 950–953. DOI:10.1145/882262 |
| [13] | 喜文飞.激光点云数据压缩的精简研究[D].昆明: 昆明理工大学, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10674-1012262251.htm |
| [14] | 翟跃华, 卢章平. 反求工程点云数据压缩技术研究[J]. 制造业自动化, 2012, 34(1): 27–28, 91. |
| [15] | 吴维勇, 王英惠. 二元Haar小波分解下的曲面数据压缩算法[J]. 小型微型计算机系统, 2003, 24(2): 309–311. DOI:10.3969/j.issn.1000-1220.2003.02.036 |


