2. 山东科技大学测绘科学与工程学院, 山东 青岛 266590
2. College of Geomatics, Shandong University of Science and Technology, Qingdao 266590, China
卫星差分码偏差也称为硬件延迟偏差(differential code biases,DCB),代表全球卫星导航系统(GNSS)中卫星和接收机不同频率之间或相同频率不同码之间的硬件延迟偏差,是卫星导航数据处理中不可忽略的误差源之一[1-4]。在美国选择可用性(SA)政策取消后,卫星差分码偏差对导航定位和授时精度的影响日趋显著,确定卫星差分码偏差的参数变得越发重要。近年来,国内一些专家、学者也对卫星硬件延迟解算进行了相关研究。文献[5]通过联合GPS和BDS观测数据建立低阶球谐函数模型进行北斗系统硬件延迟解算,结果表明北斗卫星DCB在0.3 ns左右,且稳定性较好。文献[6]就北斗卫星硬件延迟解算进行了研究和验证,并将计算结果与IGS发布的码偏差参考值进行了对比分析,结果显示误差值在0~2 ns之间,符合精度高。文献[7]对GPS卫星和接收机差分码偏差进行了实时结算,经比较模型计算DCB值与IGS最大差异不超过0.8 ns,C1、P1码延迟偏差72%差异值小于0.3 ns,P1、P2码延迟偏差74%差异值小于0.3 ns。但目前对于差分码偏差研究多局限于GPS或GPS/BDS,本文借鉴已有的成果和经验,深入开展融合BDS/GPS/GLONASS的卫星差分码偏差解算研究, 以更好地为导航定位提供服务。
1 原理与方法 1.1 观测数据预处理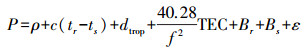 (1)
(1) 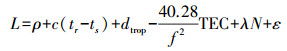 (2)
(2) 式中,P、L分别为伪距和载波相位观测值;ρ为卫星和接收机间的真实距离;tr、ts分别为接收机和卫星钟差;dtrop为对流层延迟误差;TEC为电离层总电子含量;Br、Bs分别为卫星和接收机的硬件延迟;N为载波相位测量的整周模糊度;ε表示测量噪声。
利用双频观测值可消除不同频率的电离层延迟影响,且可确定穿刺点(卫星信号传播路径与电离层的交点)的TEC值
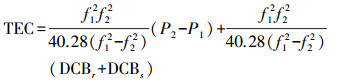 (3)
(3) 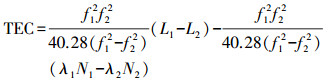 (4)
(4) 式中,f1、f2为卫星相对应的频率;DCBr=Br1-Br2,为卫星的差分码偏差;DCBs=Bs1-Bs2,为接收机差分码偏差。需要注意的是,在利用BDS、GLONASS数据进行电离层延迟模型化时,双频伪距之差转化为到总电子含量TEC时的系数f1、f2与GPS的f1、f2略有不同。
为了提高伪距的精度,在周跳探测修复后,本次试验采用载波相位平滑伪距的方法来计算电离层延迟量和频间偏差。在Hatch滤波公式的基础上,根据卫星高度角αi来确定当前观测值的权Qi=sin αi,其中i=1, 2,…,则相位平滑伪距的公式如下
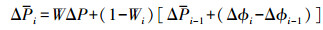 (5)
(5) 为了研究方便,一般将GNSS信号传播路径上的TEC转化为穿刺点天顶方向的总电子含量,即VTEC(vertical TEC)。电离层投影函数可以实现TEC和VTEC之间的相互转换,投影函数的种类众多,且在高度角大于20°时电离层投影函数的应用效果基本相当[11-12]。本次试验采用的是SLM(single-layer model)投影函数
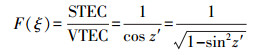 (6)
(6) 式中,F(ξ)表示投影函数;sin z′=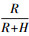
通常硬件延迟和电离层模型系数同时解算[13-15]。常用的电离层模型有三角级数模型、多项式模型、球谐函数模型等。本文试验采用与CODE分析中心相同的球谐函数模型,以15阶次的球谐函数建立VTEC模型,公式如下
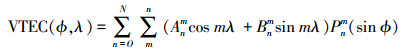 (7)
(7) 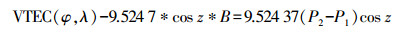 (8)
(8) 式中,φ为穿刺点的地磁纬度;λ为穿刺点的日固经度;N为球谐函数展开式的最大阶数;Pnm为规范化的勒让德函数;Anm、Bnm为全球电离层模型系数;z为卫星在穿刺点处的天顶距;所有卫星和测站的频间偏差为B,并赋予所有卫星仪器偏差总和为零的条件进行约束。
2 试验分析 2.1 数据选择iGMAS(international GNSS monitoring and assess-ment system)是我国发起的全球连续监测评估系统,iGMAS建立的目的是通过布设GNSS全球连续运行跟踪站,监测评估GNSS系统的定位精度、服务性能、可靠性和连续性等,以向全球用户提供高质量服务。中国测绘科学研究院是参与iGMAS分析中心建设的研究单位之一,全程参与系统测试与试运行。本文试验数据皆来自中国测绘科学研究院iGMAS北斗分析中心(CASM), 从IGS和CDDIS下载包含GPS、BDS、GLONASS系统的约270个全球分布均匀的测站进行全球电离层建模。
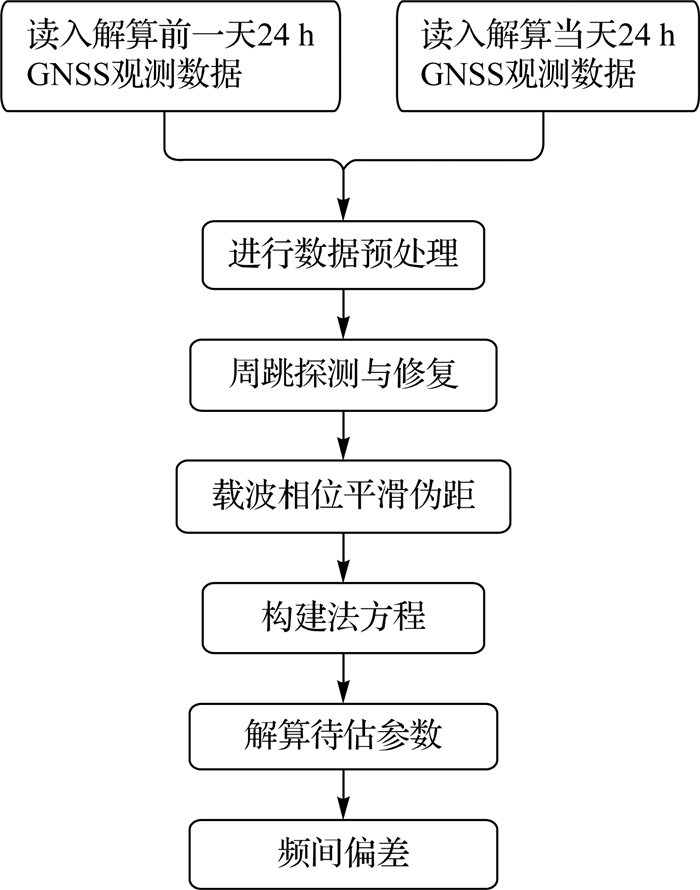
2.2 处理策略与流程由于频间偏差具有短时间内稳定的特性,因此试验采用当天观测数据和前一天观测数据同时进行解算,确保频间偏差产品天与天之间的连续性。生成频间偏差产品的流程如图 1所示。
|
| 图 1 频间偏差产品流程 |
全球电离层延迟建模中频间偏差产品一般按天解算。本文采用中国测绘科学院iGMAS北斗分析中心(CASM)2016年年积日274—306共33 d含有GPS、BDS、GLONASS系统的观测数据进行试验,共生成年积日275—305共31 d三系统频间偏差产品。以IGS发布的DCB月产品为参考,利用试验解算的频间偏差产品与CODE产品作比较,进行精度分析。
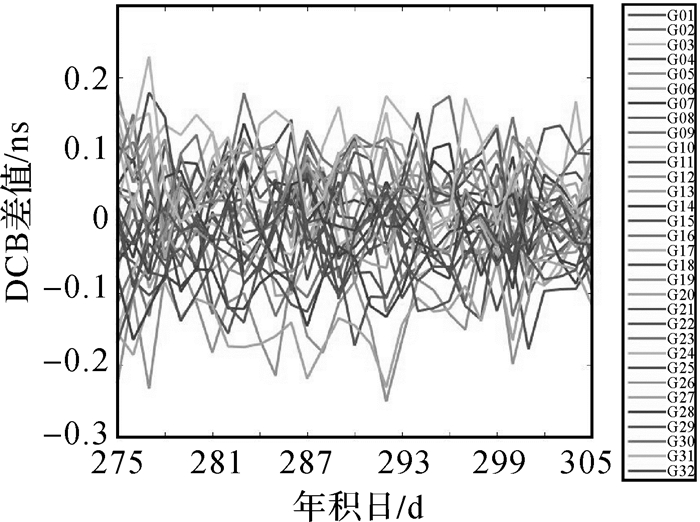
3.1 GPS卫星频间偏差精度表 1为31 d GPS系统各卫星P1P2差分码偏差的月平均值及与CODE月产品对比的精度。由表 1可知,各卫星P1P2差分码偏差精度均在0.2 ns以内,大部分在0.1 ns以内。图 2为GPS系统各卫星差分码偏差与CODE产品对比的精度随时间变化的结果。由图 2可知,各卫星差分码偏差精度均在0.3 ns以内,大部分在0.1 ns以内,说明本文解算的GPS卫星P1P2差分码偏差与CODE产品非常吻合,精度非常高,且非常稳定。
|
| 图 2 GPS系统卫星差分码偏差精度结果 |
| 卫星号 | G01 | G02 | G03 | G04 | G05 | G06 | G07 | G08 | G09 | G10 | G11 |
| DCB/ns | -7.55 | 9.02 | -5.10 | -1.47 | 2.89 | -6.76 | 3.33 | -7.19 | -4.99 | -5.50 | 3.75 |
| 精度/ns | 0.03 | 0.07 | 0.02 | 0.01 | 0.11 | 0.04 | 0.03 | 0.01 | 0.02 | 0.02 | 0.07 |
| 卫星号 | G12 | G13 | G14 | G15 | G16 | G17 | G18 | G19 | G20 | G21 | G22 |
| DCB/ns | 3.93 | 3.23 | 2.03 | 2.80 | 2.88 | 3.11 | 3.22 | 5.82 | 1.27 | 2.23 | 7.44 |
| 精度/ns | 0.03 | 0.01 | 0.03 | 0.07 | 0.06 | 0.01 | 0.02 | 0.04 | 0.13 | 0.08 | 0.02 |
| 卫星号 | G23 | G24 | G25 | G26 | G27 | G28 | G29 | G30 | G31 | G32 | |
| DCB/ns | 9.15 | -5.73 | -7.57 | -8.68 | -5.01 | 2.97 | 2.60 | -6.37 | 4.71 | -4.47 | |
| 精度/ns | 0.06 | 0.08 | 0.06 | 0.05 | 0.07 | 0.03 | 0.06 | 0.07 | 0.07 | 0.01 |
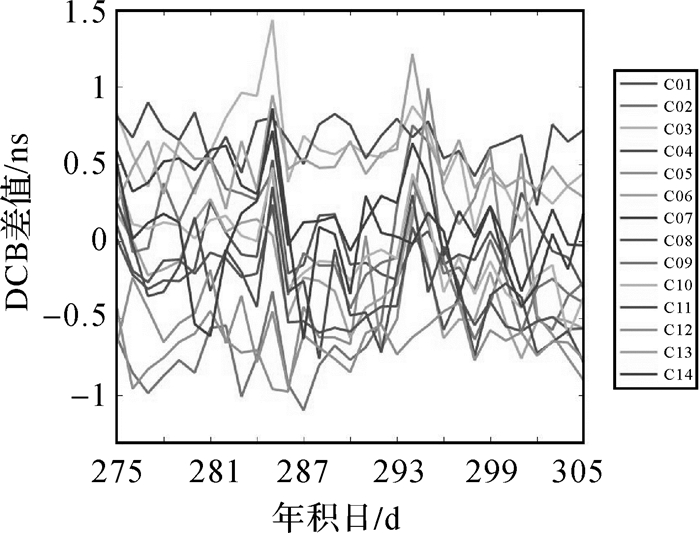
表 2为31 d BDS系统各卫星B1B3差分码偏差的月平均值及与CODE月产品对比的精度。由表 2可知,各卫星B1B3差分码偏差精度均在1 ns以内,大部分在0.6 ns以内。图 3为BDS系统各卫星差分码偏差与CODE产品对比的精度随时间变化的结果。由图 3可知,各卫星差分码偏差精度均在1.5 ns以内,大部分在1 ns以内,说明本文解算的BDS卫星B1B3差分码偏差与CODE产品基本吻合,且基本稳定。
|
| 图 3 BDS系统卫星差分码偏差精度结果 |
| 卫星号 | C01 | C02 | C03 | C04 | C05 | C06 | C07 |
| DCB/ns | 17.97 | 7.75 | 6.43 | 7.92 | 1.17 | 3.34 | 6.75 |
| 精度/ns | 0.95 | 0.53 | 0.56 | 0.81 | 0.54 | 0.25 | 0.34 |
| 卫星号 | C08 | C09 | C10 | C11 | C12 | C13 | C14 |
| DCB/ns | 4.07 | -3.09 | -4.22 | -4.73 | -3.34 | -18.87 | -1.22 |
| 精度/ns | 0.36 | 0.08 | 0.30 | 0.48 | 0.67 | 0.53 | 0.12 |
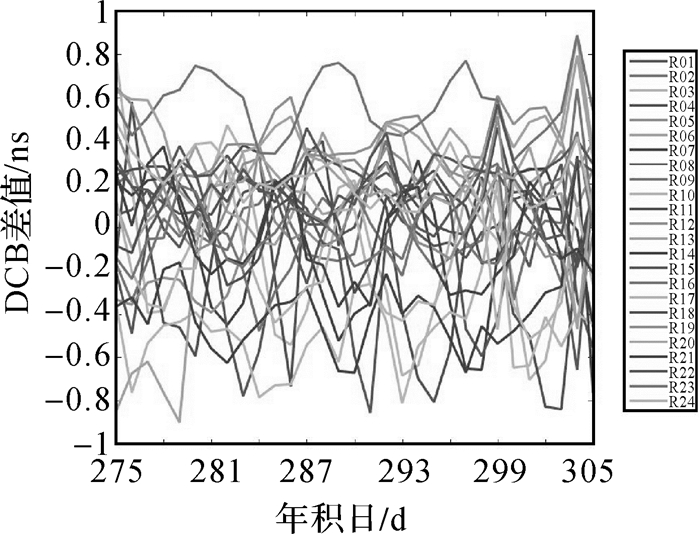
表 3为31 d GLONASS系统各卫星P1P2差分码偏差的月平均值及与CODE月产品对比的精度。由表 3可知,各卫星P1P2差分码偏差精度均在0.5 ns以内,大部分在0.3 ns以内。图 4为GLONASS系统各卫星差分码偏差与CODE产品对比的精度随时间变化的结果。由图 4可知,各卫星差分码偏差精度均在1 ns以内,大部分在0.4 ns以内,说明本文解算的GLONASS卫星P1P2差分码偏差与CODE产品相对吻合,精度较高,且比较稳定。
| 卫星号 | R01 | R02 | R03 | R04 | R05 | R06 | R07 | R08 | R09 | R10 | R11 | R12 |
| DCB/ns | -5.65 | -0.52 | 3.74 | 5.93 | 1.22 | 5.24 | 2.85 | 4.91 | 2.69 | -8.15 | 1.69 | -2.97 |
| 精度/ns | 0.02 | -0.02 | -0.16 | 0.29 | 0.21 | -0.14 | -0.28 | -0.01 | -0.48 | -0.16 | 0.14 | 0.20 |
| 卫星号 | R13 | R14 | R15 | R16 | R17 | R18 | R19 | R20 | R21 | R22 | R23 | R24 |
| DCB/ns | -1.65 | -9.74 | -3.92 | 0.62 | 2.36 | -0.79 | 5.01 | -3.03 | 2.43 | -0.61 | -7.34 | 5.82 |
| 精度/ns | 0.17 | -0.41 | 0.25 | 0.46 | -0.19 | -0.01 | 0.07 | 0.22 | -0.06 | 0.14 | -0.01 | 0.21 |
|
| 图 4 GLONASS系统卫星差分码偏差精度结果 |
对比三系统可知,GPS系统P1P2差分码偏差精度最高,且最稳定;GLONASS系统P1P2差分码偏差精度和稳定性比GPS略低;BDS系统B1B3差分码偏差精度和稳定性最低,可能是BDS星座不完善的原因。
4 结语GNSS卫星差分码偏差的确定对于提高用户的定位精度具有重要意义。本文采用中国测绘科学研究iGMAS分析中心自主研发的软件进行了试验分析,得出如下结论:
(1) GPS卫星差分码偏差精度均在0.3 ns以内,大部分在0.1 ns以内,即GPS卫星P1P2差分码偏差与CODE产品非常吻合,精度非常高,且非常稳定。
(2) BDS卫星差分码偏差精度均在1.5 ns以内,大部分在1 ns以内,即BDS卫星B1B3差分码偏差与CODE产品基本吻合,且基本稳定。
(3) GLONASS卫星差分码偏差精度均在1 ns以内,大部分在0.4 ns以内,即GLONASS卫星P1P2差分码偏差与CODE产品相对吻合,精度较高,且比较稳定。
(4) 对比三系统,GPS系统P1P2差分码偏差精度最高,且最稳定;GLONASS系统P1P2差分码偏差精度和稳定性比GPS略低;BDS系统B1B3差分码偏差精度和稳定性最低,可能是BDS星座不完善的原因。随着北斗星座的不断完善,如果采用更多的BDS观测数据一同解算,相信会得到更好的效果。
致谢: 感谢国际GNSS监测评估系统(iGMAS)中国测绘科学研究院提供的数据和技术支持。| [1] | 陈俊勇, 党亚民, 程鹏飞. 全球导航卫星系统的进展[J]. 大地测量与地球动力学, 2007, 27(5): 1–4. |
| [2] | 韩雪丽, 党亚民, 王虎, 等. 北斗卫星系统频间偏差预报模型研究[J]. 地理信息世界, 2017, 24(5): 82–85. DOI:10.3969/j.issn.1672-1586.2017.05.016 |
| [3] | 胡玉坤, 刘根友, 段鹏硕, 等. GNSS卫星中DCB的使用方法[J]. 测绘通报, 2016(5): 11–13. |
| [4] | 吴晓莉, 平劲松, 刘利, 等. 区域卫星导航系统硬件延迟解算[J]. 武汉大学学报(信息科学版), 2011, 36(10): 1218–1221. |
| [5] | 舒宝, 刘晖, 张明, 等. 北斗系统硬件延迟解算及精度分析[J]. 武汉大学学报(信息科学版), 2016, 41(2): 279–284. |
| [6] | 赵东旭, 遆鹏, 谭诗腾, 等. 一种北斗卫星差分码偏差估计方法[J]. 测绘通报, 2016(5): 14–17. |
| [7] | 张伟, 邱卫宁, 畅鑫. 基于球谐函数模型的GPS差分码延迟估计[J]. 测绘通报, 2013(6): 19–21. |
| [8] | 章红平, 施闯, 唐卫明. 地基GPS区域电离层多项式模型与硬件延迟统一解算分析[J]. 武汉大学学报(信息科学版), 2008, 33(8): 805–809. |
| [9] | SCHAER S. Mapping and Predicting the Earth's Lonospheric Using the Global Positioning System[D]. Bern: Astronomical Institute of the University of Bern, 1999. |
| [10] | PAJARES H M, JUAN J M, SANZ J, et al. The IGS VTEC Maps:A Reliable Source of Ionospheric Information Since[J]. Journal of Geodesy, 2009, 83(3-4): 263–275. DOI:10.1007/s00190-008-0266-1 |
| [11] | MANNUCCI A J, WILSON B D, YUAN D N., et al. A Global Mapping Technique for GPS-derived Ionospheric Total Electron Content Measurements[J]. Radio Science, 1998, 33(33): 565–582. |
| [12] | KLOBUCHAR J A. Ionospheric Time-delay Algorithm for Single-frequency GPS Users[J]. IEEE Transactions on Aerospace and Electronic Systems, 1987, AES-23(3): 325–331. DOI:10.1109/TAES.1987.310829 |
| [13] | 章红平, 韩文慧, 黄玲, 等. 地基GNSS全球电离层延迟建模[J]. 武汉大学学报(信息科学版), 2012, 37(10): 1186–1189. |
| [14] | 章红平. 基于地基GPS的中国区域电离层监测与硬件延迟改正研究[D]. 上海: 中国科学院上海天文台, 2006. http://cdmd.cnki.com.cn/Article/CDMD-80022-2006109504.htm |
| [15] | JIN R, JIN S, FENG G. M_DCB:Matlab Code for Estimating GNSS Sarellite and Receiver Differential Code Biases[J]. GPS Solutions, 2012, 16(4): 541–548. DOI:10.1007/s10291-012-0279-3 |


