倾斜摄影测量技术可以快速获取到地物丰富的侧面纹理信息,因此被广泛应用于城市真三维模型重建,然而由于倾斜影像间存在较大的几何变形等因素,造成倾斜影像匹配存在一定的难点。文献[1]对倾斜影像匹配时的难点进行了总结,指出影像间大倾斜角度和遮蔽区域是造成匹配点数量少、分布不均匀的主要原因。
针对倾斜影像匹配时的难点问题,国内外学者进行了大量的研究,大致可以分为两种思路:①基于仿射不变性的点特征匹配方法。具有代表性的有ASIFT[2]、Harris-Affine[3]、Hessian-Affine[4]和MSER[5]等。其中ASIFT在理论上具备完全的仿射不变性,但其效率较为低下,很难满足实际的应用需求;其余方法虽然匹配效率要远远高于ASIFT,但都不具备完全的仿射不变性,因此匹配出的同名点数量较少,且难以保证均匀分布。②基于影像纠正的倾斜影像匹配。这类方法将各个倾斜相机拍摄的影像纠正到以某一基准面为参考面的虚拟水平像片上,从而在消除影像间的几何变形后完成匹配[1]。如文献[6-7]对影像进行透视变形改正后利用SIFT算子匹配到了一定数量的连接点,由于没有考虑地形起伏的影响,且SIFT算子提取兴趣点时重现率不高,因此获取到的匹配点并不多;文献[8]引入数字高程模型对倾斜影像进行变形改正,然后利用特征检测和独立二元稳健初级特征描述子获取纠正影像的特征点;文献[9]在纠正影像上提取了高斯差分特征点;文献[10]利用重现率较高的Harris算子获取特征点,在建筑物密集的影像上得到了较好的匹配结果,但对于角点特征较少的特殊区域,该算子提取到的特征点数量不多;文献[11]对文献[10]的匹配算法进行了改进,同时获取Harris角点和高斯差分特征点,得到了更为密集的匹配结果。
综上所述,特征点检测算子和匹配速度是影响倾斜影像匹配的关键因素。鉴于此,本文在获取透视变形纠正后的影像后,对影像分块并构建金字塔,在顶层金字塔影像块上利用Dense SIFT[12]算子获取密集、均匀分布的采样点,并利用改进的最小二乘匹配算法对初始匹配点精化,得到最终的匹配结果。通过选取典型区域的倾斜影像进行匹配试验,从匹配点数量、分布均匀度和匹配效率上验证本文方法的有效性。
1 倾斜影像连接点自动匹配方法 1.1 倾斜影像预处理(影像透视变形纠正)倾斜摄影相机平台在出厂时一般都会经过严格的相机标定,即每个相机相对于摄影平台的姿态参数已知,此时可由姿态参数和影像的POS信息计算每张影像相对于大地坐标系的粗略外方位元素[14]。
对影像进行纠正时,根据飞行时的设计航高,在物方平面上假定一个平均高程面π,然后利用式(1)可得到影像4个角点对应在物方高程面π上的4个地面点坐标。
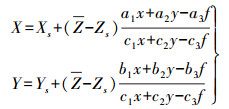 (1)
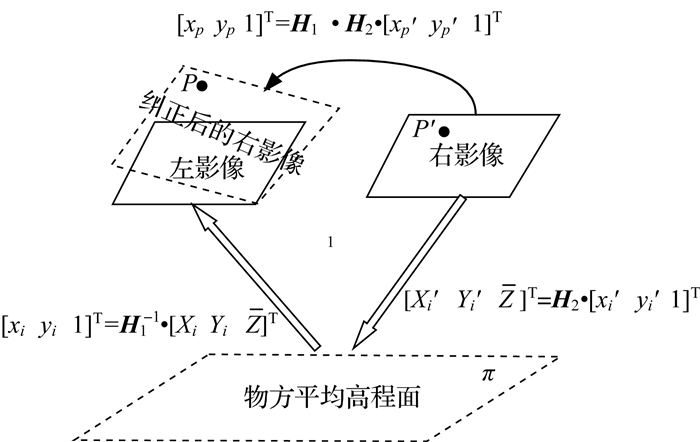
(1) 式中,Xs、Ys、Zs为初始的粗略外方位线元素;a1、a2、…、c3为旋转矩阵的9个元素;f为焦距;Z为由所有影像的外方位线元素均值与设计航高计算得到的平均高程值;(X, Y)为影像角点(x, y)投影到平均高程面的平面坐标。影像纠正过程如图 1所示,通过计算影像与高程面π的透视变换矩阵H1、H2,可以得到左右影像之间的透视变换矩阵H=H1-1·H2,利用H矩阵可以将右影像逐像素地变换至纠正后的影像上,纠正后的影像相比于左影像仅存在地形起伏引起的像点位移,尺度和旋转所引起的变形基本消除。
|
| 图 1 影像纠正过程 |
为了避免不必要的特征提取和匹配时间,在获取影像的匹配点时,利用影像间位置关系获取影像间重叠区域,然后对重叠区域的影像进行分块,在较小的影像块之间进行匹配。其优点是:一方面影像块内提取的特征点数量较少,减少了匹配的计算时间;另一方面,在影像块间估计的单应矩阵表达的像点透视变换对应关系也更加精确(影像块范围较小,更加接近于平面),增加了粗差剔除的精度。
1.2 Dense SIFT匹配 1.2.1 Dense SIFT采样点获取Dense SIFT算子最初用于模式识别领域[12],其特点是在特征点检测阶段不计算高斯尺度空间,而是对影像进行高斯平滑操作后采用一定的步长在影像上获取采样点(Dense SIFT特征点),该算子检测特征点时的重现率不依赖于影像特征信息量,因此可以获取到密集、均匀分布的特征点。
Dense SIFT算子获取采样点时,在采样范围内以一定步长滑动特征描述窗口,滑动的过程中记录窗口中心点坐标和特征向量。特征点描述过程如图 2所示,以采样点p=(x, y)∈I为中心(I表示影像范围),统计采样点特征描述窗口内像素8个方向的梯度,此时采样点p的描述向量就可以表示为4×4×8=128维度的特征向量。

|
| 图 2 采样点特征描述 |
为减少Dense SIFT特征点的冗余度,本文对分块后的影像建立金字塔,在顶层金字塔影像块上按照一定步长(步长设置为5)获取Dense SIFT密集采样点。图 3所示为降采样影像块获取的采样点,采样点可以较好地表达图像局部特征,且初始同名点(图 3中椭圆内的点)与真实同名点仅存在少许的偏移量,只需对同名点的位置改正即可得到较为准确的匹配结果。

|
| 图 3 降采样影像获取的采样点 |
Dense SIFT算子获取的特征点数量较多,为了减少匹配时间,本文对左右影像块的Dense SIFT特征点构建二维KD树,利用影像间的透视变换关系计算匹配点的大致位置,通过KD树搜索邻近点后利用比值提纯法获取最终的匹配点。假设左右影像分别提取到m、n个采样点,则利用文献[15]穷举法和本文匹配算法的计算复杂度分别为:
(1) 穷举法:O(m, n)=mn。
(2) 本文方法:假设左右影像分块数为10块,KD树搜索周围40个临近点,则匹配的计算复杂度为O(m, n)=(m/10)×40×10=40m。
对300×300大小的影像分块后进行匹配试验(分块大小为100×100像素),本文匹配方法的效率比穷举法快4倍以上。
获取粗匹配点后,基于RANSAC算法剔除粗差即可得到最终匹配结果。图 4为纠正后的降采样倾斜影像匹配结果,可以看出,Dense SIFT算子相比于SIFT算子获取到了更多的匹配点,尽管这些匹配点精度不高,但只需进行坐标改正即可得到较为精确的匹配结果。

|
| 图 4 纠正后的降采样倾斜影像匹配结果 |
为了获取精确的同名点,本文对最小二乘匹配算法进行改进后获取Dense SIFT初始匹配点的精确坐标,其基本原理是通过减少最小二乘匹配模型中附加参数来增大匹配时的拉入范围(原始最小二乘匹配算法的拉入范围在1~2个像素以内[16])。针对倾斜影像特点对附加参数进行分析如下:
(1) Dense SIFT匹配出的同名点会偏离真实像点几个像素,在模型中主要表现为像点的平移,因此需要考虑模型中的平移参数a0、b0。
(2) 透视变形改正后的影像间像点位移具有较强的规律性。如上下影像最小二乘匹配时,变形主要发生在行方向,可以仅考虑行方向尺度变形参数b2(变形主要发生在影像行方向上);左右影像最小二乘匹配时,仅考虑列方向尺度变形参数a1。
(3) 采用相关系数作为匹配测度可以避免辐射变形的影响,因此在模型中可以不考虑辐射变形改正参数h0、h1。
综合考虑上述因素,将原始的最小二乘匹配模型修改如下
 (2)
(2) 式中,g1、g2分别为左右影像像元的灰度;n1、n2为左右影像噪声;a0、a1、b0、b2为右影像窗口的仿射变形改正参数。线性化后的误差方程如下
 (3)
(3) 式中,da0、da1、db0、db2是待定参数的改正值;Δg=g1-g2;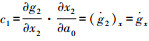
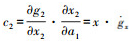


像点坐标改正时,首先在影像块内随机选取至少20对初始匹配点作为种子点,利用改进的最小二乘匹配算法计算匹配点的平均坐标改正值,将其视为系统误差对所有匹配点进行坐标改正。然后在改正的基础上再次利用改进最小二乘匹配方法获取所有匹配点的精确位置,并对相关系数小于0.85的匹配点进行剔除。试验发现,当匹配窗口大小为17时,改进的最小二乘匹配算法的平均拉入范围达到3个像素以上,可以有效地改正初始匹配点。
1.4 获取原始纠正影像匹配点假设第i层影像的匹配点坐标为(xi, yi),则将其换算到i-1层影像上,坐标为(2xi, 2yi),利用改进的最小二乘匹配算法对i-1层影像上的所有匹配点进行坐标改正,可得到本层的匹配点对。在每层金字塔影像上重复此过程,可得到原始纠正影像上的匹配点。
2 试验结果与分析试验使用ISPRS提供的IGI Penta DigiCAM倾斜相机平台(有1台下视相机和4台侧视相机,前、后、左、右各一台,摄影倾角都均为45°)获取的倾斜影像数据进行试验。基于Matlab 2015b设计了匹配算法,试验的硬件平台为华硕PU403UF笔记本,处理器为Intel i7-6500U,主频2.5 GHz,内存8 GB。
为验证本文算法的有效性,选取两组典型地区(乡村和城区)的倾斜影像数据进行匹配试验,影像数据见表 1。对于区域1(乡村地区),将286与290影像视为第一组,218与290影像视为第二组,286与218视为第三组;对于区域2(城区),将146与140影像视为第一组,146与254影像视为第二组,140与254影像视为第三组。
| 区域 | 影像编号 | 拍摄位置 |
| 乡村 | 290 | 航带1第1摄站下视 |
| 286 | 航带1第5摄站前视 | |
| 218 | 航带5第1摄站左视 | |
| 城区 | 146 | 航带9第1摄站下视 |
| 140 | 航带9第7摄站前视 | |
| 254 | 航带3第1摄站右视 |
为定性分析本文方法的匹配效果,在降采样的影像上分别用SIFT、ASIFT、Visual SFM和本文算法获取两个典型区域(乡村和城区)影像的匹配点,结果见表 2。
| 区域 | 匹配像对 | 本文方法 | SIFT | ASIFT | Visual SFM |
| 乡村 | 286-290 | 1275 | 134 | 395 | 64 |
| 218-290 | 1426 | 93 | 291 | 97 | |
| 286-218 | 402 | 12 | 41 | 9 | |
| 城区 | 146-140 | 1321 | 55 | 477 | 66 |
| 146-254 | 1624 | 47 | 401 | 80 | |
| 140-254 | 365 | 33 | 58 | 63 |
可以看出,本文方法相比于SIFT、ASIFT及Visual SFM能够获取到数量更多的匹配点。为进一步验证匹配结果的正确性,对两个典型区域的局部匹配结果进行放大显示,结果如图 5、图 6所示。

|
| 图 5 区域1匹配结果 |

|
| 图 6 区域2匹配结果 |
从典型区域的匹配结果可以看出,本文方法不论在建筑物密集的城区还是在地形平坦的区域,都获取到了一定数量的匹配点,且匹配点分布较为均匀;在纹理贫乏的平坦路面和林地,本文方法也获取到了一定数量的匹配点,说明本文方法适用性较好;在几何变形较大的林地(如图 6(d)所示),由于这些区域地物形变较大,因此得到的匹配点数量不多。
为定量评价本文方法获取的匹配点精度,在本文匹配点的基础上,利用传统的最小二乘匹配算法获取更为精确的同名点作为参考值,通过计算坐标差值反映匹配误差,同时对匹配误差进行统计分析,剔除不符合正态分布的粗差后,计算中误差作为精度评价指标,计算结果见表 3。
| 像素 | |||||
| 区域2 | X方向 | Y方向 | |||
| 最大误差 | 中误差 | 最大误差 | 中误差 | ||
| 大型建筑物 | 0.651 2 | 0.180 2 | 0.732 8 | 0.212 8 | |
| 小建筑物 | 0.554 6 | 0.174 8 | 0.543 | 0.180 2 | |
| 平坦路面 | 0.474 6 | 0.135 4 | 0.575 3 | 0.160 7 | |
| 平坦路面和林地 | 0.732 1 | 0.237 2 | 0.835 4 | 0.269 6 | |
从表 3中可以看出,4个区域的匹配点精度在0.3个像素以内。密集小型建筑物的匹配精度最高,这主要是由于该区域影像变形较小,同时纹理信息又比平坦路面的影像更为丰富,因此提取的Dense SIFT匹配点较为稳定,匹配精度较高。
2.2 算法计算效率对比分析在相同的测试环境下,分别用SIFT、ASIFT和本文方法对降采样一倍后影像的计算匹配时间进行对比分析,结果见表 4。可以看出,本文算法在两个典型区域的匹配耗时仅为SIFT算法的一半左右,相比于ASIFT算法的用时更少,速度最快提升了700倍,说明本文方法具有较高的匹配效率。
| s | ||||
| 区域 | 像对 | 算法匹配耗时 | ||
| SIFT | ASIFT | 本文方法 | ||
| 乡村 | 286-290 | 16.55 | 3056 | 8.12 |
| 218-290 | 16.24 | 3013 | 8.16 | |
| 286-218 | 19.78 | 3301 | 5.04 | |
| 城区 | 146-140 | 17.21 | 2997 | 8.17 |
| 146-254 | 16.90 | 803091 | 9.30 | |
| 140-254 | 23.56 | 3570 | 5.10 | |
为解决倾斜摄影影像连接点少、分布不均匀和匹配效率低等问题,本文提出了一种基于Dense SIFT与改进最小二乘匹配结合的连接点自动获取方法,对典型区域的影像进行匹配试验。结果表明:本文方法能够获取到密集且均匀分布的连接点,且相比于SIFT和ASIFT算法,本文算法匹配效率更高,获取的匹配点精度优于0.3个像素。下一步的研究方向是:①从Dense SIFT的匹配结果中获取更加稳定的匹配点,提高匹配精度;②研究更加稳健的误匹配点剔除方法,尽可能保留更多的正确匹配点;③实现算法的并行化,减少匹配时间。
| [1] | 袁修孝, 陈时雨. 倾斜航摄影像匹配方法探究[J]. 测绘地理信息, 2015, 40(6): 1–6. |
| [2] | MOREL J M, YU G. ASIFT:A New Framework for Fully Affine Invariant Image Comparison[J]. Siam Journal on Imaging Sciences, 2010, 2(2): 438–469. |
| [3] | MIKOLAJCZYK K, SCHMID C. Scale and Affine Invariant Interest Point Detectors[J]. International Journal of Computer Vision, 2004, 60(1): 63–86. DOI:10.1023/B:VISI.0000027790.02288.f2 |
| [4] | MIKOLAJCZYK K, SCHMID C. An Affine Invariant Interest Point Detector[C]//European Conference on Computer Vision. [S. l. ]: Springer-Verlag, 2002: 128-142. |
| [5] | FORSSEN P E. Maximally Stable Colour Regions for Recognition and Matching[C]//IEEE Conference on Computer Vision and Pattern Recognition. Minneapolis: IEEE, 2007: 1-8. |
| [6] | 赵霞, 朱庆, 肖雄武, 等. 基于同形变换的航空倾斜影像自动匹配方法[J]. 计算机应用, 2015, 35(6): 1720–1725. DOI:10.3969/j.issn.1001-3695.2015.06.026 |
| [7] | 闫利, 费亮, 叶志云, 等. 大范围倾斜多视影像连接点自动提取的区域网平差法[J]. 测绘学报, 2016, 45(3): 310–317. |
| [8] | HU H, Zhu Q, Du Z, et al. Reliable Spatial Relationship Constrained Feature Point Matching of Oblique Aerial Images[J]. Photogrammetric Engineering and Remote Sensing, 2015, 81(1): 49–58. |
| [9] | 肖雄武, 郭丙轩, 李德仁, 等. 一种具有仿射不变性的倾斜影像快速匹配方法[J]. 测绘学报, 2015, 44(4): 414–421. |
| [10] | 肖雄武, 李德仁, 郭丙轩, 等. 一种具有视点不变性的倾斜影像快速匹配方法[J]. 武汉大学学报(信息科学版), 2016, 41(9): 1151–1159. |
| [11] | 李德仁, 肖雄武, 郭丙轩, 等. 倾斜影像自动空三及其在城市真三维模型重建中的应用[J]. 武汉大学学报(信息科学版), 2016, 41(6): 711–721. |
| [12] | VO T, TRAN D, MA W. Tensor Decomposition of Dense SIFT Descriptors in Object Recognition[C]//Proceedings of ESANN. Belgium: [s. n. ], 2014. |
| [13] | KAKDE H M. Range Searching Using Kd Tree[EB/OL]. 2005-08-25. http://www.cs.utah.edu/~lifeifei/cs6931/kdtree.pdf. |
| [14] | 张祖勋, 张剑清. 数字摄影测量学[M]. 武汉: 武汉大学出版社, 2012. |
| [15] | LOWE D G. Distinctive Image Features from Scale-invariant Keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91–110. DOI:10.1023/B:VISI.0000029664.99615.94 |
| [16] | 陶闯. 一种SPOT影像参数动态筛选的最小二乘匹配方法[J]. 武汉大学学报(信息科学版), 1993, 18(2): 31–39. |


