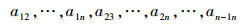2. 辽宁师范大学计算机与信息技术学院, 辽宁 大连 116029
2. College of Computer and Information Technology, Liaoning Normal University, Dalian 116029, China
由于高光谱影像具有分辨率高、地球表面信息丰富、地物光谱曲线连续、能清晰识别地物的细微特征等优点,目前,高光谱遥感技术越来越多地被应用于各个学科领域[1]。但是高光谱遥感影像数据量大且存在大量的数据冗余[2]。因此,在降低高光谱数据维数的同时,尽量保持原始波段中蕴含的信息,并采用合适的分类器进行分类,是获取高光谱遥感数据中有用信息的重要手段。
谱聚类(spectral clustering)方法是一种简单有效的聚类方法[3]。该方法以图谱理论为依托,根据遥感影像的光谱信息,定义了一个相似度矩阵。计算该矩阵的特征值和特征向量,然后通过选择合适的特征向量进行降维和聚类[4]。只利用遥感影像光谱信息,忽视了地物目标的空间结构特征,往往导致分类精度不理想,不能全面准确地表达地理数据的信息特征[5]。为了弥补只利用光谱信息进行聚类的不足,进一步提高分类精度,考虑将像素点的光谱信息与空间信息有机地结合起来。
本文在谱方法的基础上,借助高光谱图像中像素点的邻居信息、部分类标签信息和高斯核函数给出了一种新的度量样本点之间相似度的函数。基于定义的相似度函数和K近邻方法(KNN)构造图,在图的构建中加入空间信息,并赋权值,在遗传算法中通过不断变异和优化的方法得到了最佳的图。对于降维后的数据,结合局部平均伪近邻算法对数据进行聚类分析。试验结果表明了所提出方法的可行性。
1 预备知识 1.1 谱方法假设图G=(V, E),其中V是点的集合,E是边的集合。W是其对应的邻接矩阵。将邻接矩阵W的每行元素相加为对角元素构成对角矩阵,用D表示。
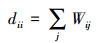 (1)
(1) 广义的特征值问题被定义为
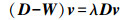 (2)
(2) 式中,λ为特征值;v为λ所对应的特征向量。
规范Laplacian矩阵有如下形式
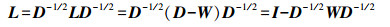 (3)
(3) 式中,I为单位矩阵。
求解式(3)中L的特征值问题,不妨假设其前d个最大特征值为λ={λ1, λ2, …, λd},对应的特征向量构成的矩阵是V={v1, v2, …, vd},即为所求的映射,然后用k-means等聚类算法对降维后的数据进行分类。
一般来说,构建邻接矩阵W的方法有2种:ε-邻近法,K近邻法[6]。本文采用的是K近邻法。
1.2 局部平局伪近邻(LMPNN)LMPNN[7-8]首先在每类中寻找待测样本点的k个最近邻,并计算k个近邻点的局部平均向量,然后采用k个局部平均向量(均值向量)计算和预测该样本点的类标签。
设训练样本数为N,令N1, N2, …, Nm表示对应类C1, C2, …, Cm的训练样本数,Xj={xj(i)},i=1, 2, …, Nj,表示属于类别Cj的训练样本数据集。
具体步骤如下:
(1) 首先从每个类别Cj中找到待测样本x的k个最近邻,表示为xj1, xj2, …, xjk,j=1, 2, …, m,然后计算两点间欧氏距离并按递增顺序排列,表示为
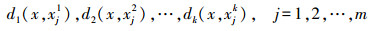 (4)
(4) (2) 计算每类Cj中x的前k个近邻点的均值向量uj(i)表示为
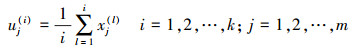 (5)
(5) 式中,测试样本x与k个均值向量的欧氏距离为:d(x, uj(1)), d(x, uj(2)), …, d(x, uj(k)),且已按递增顺序排列。
(3) 定义权重,距离越近权重值越大,在类Cj中第i个局部平均向量uj(i)的权重Wji定义为
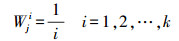 (6)
(6) (4) dj表示测试样本x与类Cj中的局部均值向量的距离加权和,则有
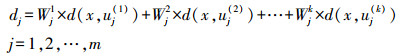 (7)
(7) (5) 预测类标签:将距离x最近的基于局部平均伪近邻的类标签赋给x,则有
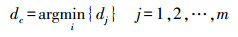 (8)
(8) 仅仅使用高光谱图像中像素点的光谱信息进行分类时,不能全面准确地表达地理数据的信息特征。本文提出的方法考虑了高光谱数据空间一致性的特点,在构图时加入空间信息,将地理空间近邻像元点的信息加入到图的构建中,从而增强地理空间邻域像元的紧密性,试图保持原高维空间中数据的类结构。
给定一幅高光谱图像HSI,像素数据集为HSI={x1, x2, …, xn}, xi∈Rd(i=1, 2, …, n),n为像素点个数。每类随机标记少量像素点,同时从像素数据中随机选取部分无标记数据,共同组成训练集。在IGASC算法中,如果点xi与近邻点xj属于同类,或近邻或空间位置近邻,则连起来构成图G。
本文采用的是像素点xi的Moore邻居,定义如下
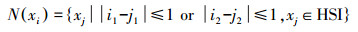 (9)
(9) 式中,(i1, i2)为像素点xi的空间位置坐标。
定义新的相似度矩阵W
 (10)
(10) 式中,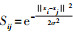
W′ij被定义为
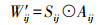 (11)
(11) 式中,A为一个对HSI通过KNN方法构造的相似图的邻接矩阵;Aij表示A中的第i行第j列元素;⊙表示2个矩阵对应元素相乘。
2.2 遗传优化本文应用遗传算法[9],KNN相似图的优化问题被适当地转换成染色体问题,优化问题被定义为
 (12)
(12) 式中,Aij∈{0, 1}表示KNN邻接矩阵A中的第i行第j列元素。优化过程描述如下:
2.2.1 构建初始种群分别计算k=3, 4,…, M时的KNN矩阵A,由于A是对称矩阵,因此只提取每个邻接矩阵的上三角元素就能代表全部信息,可表示为
构成由M-2条染色体组成的初始种群pop(0)。
为了丰富种群,转换小部分数据,即随机提取一定比例的元素把“0”元素转换成“1”,反之亦然。
2.2.2 适应度评估在本文提出的算法中,分类精度指标OA被用作适应度函数f(x)。
2.2.3 遗传算子(1) 选择:采用轮盘赌选择法[9],每条染色体被选择的概率pi和其适应度值fi成正比。
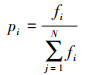 (13)
(13) (2) 交叉:本文选用的是单点交叉,交叉概率设置为0.7,在每一组染色体中随机的选择一个交叉点,所形成的子序列分别进行交换。
(3) 变异:随机选择染色体的一部分经历突变,即“0”变成“1”,或“1”变为“0”,试验中突变率设置为0.1。此外,为了保证新产生的染色体不改变太多,随机选取一定比例的元素把“1”变成“0”,然后在随机取相同数量的元素把“0”变成“1”。
2.2.4 谱方法遗传算子在染色体上的应用,形成新一代种群pop(1)。重建KNN矩阵A,分别把pop(1)中的每一条染色体转换成KNN矩阵,因此结合空间近邻信息的谱方法即可执行,然后利用局部平均伪近邻算法(LMPNN)进行分类。
2.2.5 适应度排序下一步是计算所有新产生的染色体的适应度值,并将它们与父代染色体的适应度值一同排序,只保留前M-2个较高适应度值的染色体。
已经达到50代最大,或当连续5代没有被优化的标准改变,该算法终止。
2.3 IGASC的算法描述基于上面的谱方法和遗传算法,给出本文所提出算法的详细步骤。
输入:像素数据集HIS。
输出:分类精度指标OA值。
(1) 从数据集中按一定比例标记少量样本点,同时从数据集中剩余部分随机选取部分无标签的数据,共同组成训练集。
(2) 根据式(10)、式(11)构图G,构造图的权重矩阵W。
(3) 调用2.2中的遗传算法优化图。
(4) 利用2.1中的谱方法进行降维。
(5) 利用1.2中描述的LMPNN算法对所有像素点分类。
3 试验本文选择在高光谱图像分类中常用的SalinasA数据集和Botswana数据集上进行试验,说明本文方法的有效性。试验结果采用分类精度指标OA值来衡量,OA值越大,说明分类结果越精确。将本文提出的算法与其他算法进行比较,结果表明本文提出的算法分类精度较高。
SalinasA图像数据是Salinas图像的一部分,是加利福尼亚萨利纳斯山谷地区,由AVIRIS传感器获取,每个波段由83×86个像素点组成,共224个波段,去除噪声波段,用于试验分析的波段数是204个。包含6类地物,地物真实分类情况如图 1(a)所示。

|
| 图 1 SalinasA数据 |
由表 1可以看出,在随机选取40%像素点作为训练样本(其中2%带标签,38%无标签),其余作为测试样本的情况下,本文算法的分类精度高于传统的谱方法与K近邻、局部平均伪近邻等结合的算法,同样高于遗传优化谱方法与K近邻结合算法,高光谱图像分类结果如图 1(b)所示。表 2给出了在随机选取40%像素点作为训练样本(其中1.1%带标签,38.9%无标签),其余作为测试样本的情况下,本文算法相对于无监督的谱聚类、K-means和WSS-SC算法,分类精度提升13%~31%,相对于半监督算法SVM、LapSVM和SSG+W,分类精度提升1.4%~8%。
| (%) | |
| 算法 | OA |
| SC+KNN | 97.63 |
| SC+LMPNN | 97.77 |
| GASC+KNN | 98.41 |
| IGASC+LMPNN | 98.78 |
Botswana数据是南非博茨瓦纳奥卡万戈三角洲地区影像,由搭载在NASA的EO-1卫星上的Hyperion传感器获取。该影像空间分辨率达30 m,由1476×256个像素组成,共242个波段,波长范围是400~2500 nm,经过辐射校正,去除噪声、大气吸收波段,用于试验分析的是145个波段,共14种地貌类别,真实影像如图 2(a)所示。

|
| 图 2 Botswana数据 |
由表 3可以看出,在随机选取20%像素点作为训练样本(其中10%带标签,10%无标签),其余作为测试样本的情况下,本文算法的OA值是90.15%,影像分类结果如图 2(b)所示,高于传统的谱方法与K近邻、局部平均伪近邻相结合的算法,同样高于遗传优化谱方法与K近邻结合算法。此外将提出的算法与K-means、FCM、SSGC和SSGCK算法进行比较,见表 4,可以看出随机标记10%时,本文提出算法的总体分类精度就高于以上4种算法,标记15%时,分类精度达到94.27%。
| (%) | |
| 算法 | OA |
| SC+KNN | 88.08 |
| SC+LMPNN | 88.98 |
| GASC+KNN | 89.36 |
| IGASC+LMPNN | 90.15 |
本文提出了一种基于空间信息和遗传算法的半监督高光谱图像分类方法。该方法的核心内容是根据空间信息、少量类标签信息和部分无标记数据组成训练样本集,结合高斯核函数定义新的相似度函数,构造出图G。通过遗传算法不断优化相似图,然后应用局部平均伪近邻对降维后的数据进行分类。本文提出的算法可以有效解决高光谱图像半监督分类问题,具有很好的实用性。并且本文提出的方法还可以用于人脸识别、语音分析、降维等方面,具有很好的通用性。
| [1] | 田彦平, 陶超, 邹峥嵘, 等. 主动学习与图的半监督相结合的高光谱影像分类[J]. 测绘学报, 2015, 44(8): 919–926. |
| [2] | 丁胜, 袁修孝, 陈黎. 粒子群优化算法用于高光谱遥感影像分类的自动波段选择[J]. 测绘学报, 2010, 39(3): 257–263. |
| [3] | SCHAEFFER S E. Survey:Graph Clustering[J]. Computer Science Review, 2007, 1(1): 27–64. DOI:10.1016/j.cosrev.2007.05.001 |
| [4] | CHRYSOULI C, TEFAS A. Spectral Clustering and Semi-supervised Learning Using Evolving Similarity Graphs[J]. Applied Soft Computing, 2015, 34(C): 625–637. |
| [5] | 杨钊霞, 邹峥嵘, 陶超, 等. 空-谱信息与稀疏表示相结合的高光谱遥感影像分类[J]. 测绘学报, 2015, 44(7): 775–781. |
| [6] | LUXBURG U. A Tutorial on Spectral Clustering[J]. Statistics and Computing, 2007, 17(4): 395–416. DOI:10.1007/s11222-007-9033-z |
| [7] | GOU J, DU L, ZHANG Y, et al. A New Distance-weighted K-nearest Neighbor Classifier[J]. Journal of Information and Computational Science, 2012, 9(6): 1429–1436. |
| [8] | GOU J, ZHAN Y, RAO Y, et al. Improved Pseudo Nearest Neighbor Classification[J]. Knowledge-based Systems, 2014, 70(C): 361–375. |
| [9] | SABA F, VALADANZOU M J, MOKHTARZADE M. The Optimazation of Multi Resolution Segmentation of Remotely Sensed Data Using Genetic Alghorithm[J]. ISPRS-international Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2013, 40(1): 345–349. |
| [10] | 何芳, 贾维敏, 王标标, 等. 基于加权空-谱联合的遥感图像聚类[C]//国家安全地球物理丛书(十二)——地球物理与信息感知. 鞍山: [s. n. ], 2016: 5. |
| [11] | BELKIN M, NIYOGI P, SINDHWANI V. Manifold Regularization:A Geometric Framework for Learning from Labeled and Unlabeled Examples[J]. Journal of Machine Learning Research, 2006, 7(1): 2399–2434. |
| [12] | CAMPS-VALLS G, MARSHEVA T V B, Zhou D. Semi-supervised Graph-based Hyperspectral Image Classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(10): 3044–3054. DOI:10.1109/TGRS.2007.895416 |
| [13] | 邬文慧. 空谱联合高光谱遥感图像半监督分类[D]. 西安: 西安电子科技大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10701-1015437450.htm |
| [14] | XIE J, GUO W, XIE W, et al. K-means Clustering Algorithm Based on Optimal Initial Centers Related to Pattern Distribution of Samples in Space[J]. Applications Research of Computers, 2012, 29(3): 888–892. |
| [15] | KANNAN S R, RAMATHILAGAM S, CHUNG P C. Effective Fuzzy C-means Clustering Algorithms for Data Clustering Problems[J]. Expert Systems with Applications, 2012, 39(7): 6292–6300. DOI:10.1016/j.eswa.2011.11.063 |
| [16] | 李志敏, 郝盼超, 黄鸿, 等. 半监督复合核图聚类在高光谱图像中的应用[J]. 光电工程, 2016, 44(4): 33–39. DOI:10.3969/j.issn.1003-501X.2016.04.006 |