浮动车数据在探索兴趣点、更新道路网络、预测交通、寻找最优路径等领域扮演了一个重要角色[1]。在实际应用过程中,由于GPS设备自身局限性及环境噪声干扰等因素[2],车辆定位位置与实际运行位置之间存在偏差,这直接影响着后期的分析工作。地图匹配算法可以将定位数据匹配到正确的行驶路段上,有效解决定位偏差问题[3-4]。现有的地图匹配算法主要分为基于几何信息的地图匹配算法、基于拓扑关系的地图匹配算法、基于概率统计的地图匹配算法及先进的地图匹配算法[5]。基于几何信息的地图匹配算法提出时间较早,只考虑几何信息而忽略了道路的连接性[6];基于拓扑关系的地图匹配算法采用拓扑逻辑信息如路段连通性、道路方向和道路属性[7];基于概率统计的地图匹配算法利用概率统计理论确定候选道路集、导航传感器的误差源及空间道路数据[8];先进的地图匹配算法主要采用人工智能的方法[9]。
DIANGE Y等在2011年提出了一种采用综合模糊评价方法评估轨迹相似性,对位置、形状、方向和行为方面的相似性进行量化[10];肖维丽等在2015年提出了基于高程的改进D-S证据理论地图匹配算法,通过引入高程信息提高了算法在复杂路况下的匹配准确度,但单点匹配耗时较高,无法满足实时性的需求[11];王美玲等在2012年提出了浮动车地图匹配算法,通过距离权重、航向权重及基于最短路径的可达性权重确定最优匹配道路,相较于传统基于权重的地图匹配算法引入可达性权重,提高了匹配的准确度,但其对于最短路径信息应用仅限于可达与非可达,对于同样可达的路段缺乏辨识度,在一定程度上限制了匹配准确度[12];曾喆等在2015年提出了曲率积分约束的浮动车地图匹配算法,通过曲率积分度量轨迹曲线弯曲程度,以此作为前后定位点间关联特性实现地图匹配过程,在一定程度上提高了匹配精度,当采样间隔大于100 s时,匹配准确度急剧降低[13];刘卫宁等在2016年提出了基于时空分析的地图匹配算法,通过构建网格索引方式提高了候选路段的确定速率,综合考虑几何及路网拓扑等信息提高匹配准确度,但其未考虑网格索引中空网格问题且忽略了车辆航向信息,限制了其匹配的准确度[14]。
浮动车数据考虑传输成本及存储成本,通常采用低频(60 s间隔及以上)采样的方式[15],相邻定位点之间通过多个路段,两个相邻定位点之间拓扑缺失。现有地图匹配算法应用于低频方式采样的浮动车GPS数据时存在匹配准确度与匹配效率不能同时兼顾的问题。
针对此问题,本文提出了一种改进的浮动车地图匹配算法,采用改进的自适应网格划分方法快速确定候选路段集,基于司机驾驶习惯采用最短路径信息建立前后定位点间联系性,考虑单个定位点航向偶然性较大问题加入前后定位点间轨迹方向信息,基于最短距离权重、车辆航向权重、最短路径权重及轨迹方向权重的总权重准确确定最优匹配路段及匹配点。
1 改进的浮动车地图匹配算法改进的浮动车地图匹配算法流程如图 1所示。

|
| 图 1 地图匹配算法流程 |
地图匹配过程主要分为确定候选路段集与确定最优匹配路段两个步骤。本文算法基于改进自适应网格划分方法快速确定候选路段集,基于最短距离权重、车辆航向权重、最短路径权重及轨迹方向权重的总权重准确确定最优匹配路段及匹配点。
1.1 网格划分算法 1.1.1 基本网格划分算法基本的网格划分方法是将电子地图按照步长l,依照从左到右、从下到上的规则进行网格划分,划分为M×N个l×l的正方形独立网格,网格编号为j(j=1, 2, …, MN-1)。某一初始定位点P1经纬度坐标为(x, y),其落入的网格编号j
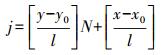 (1)
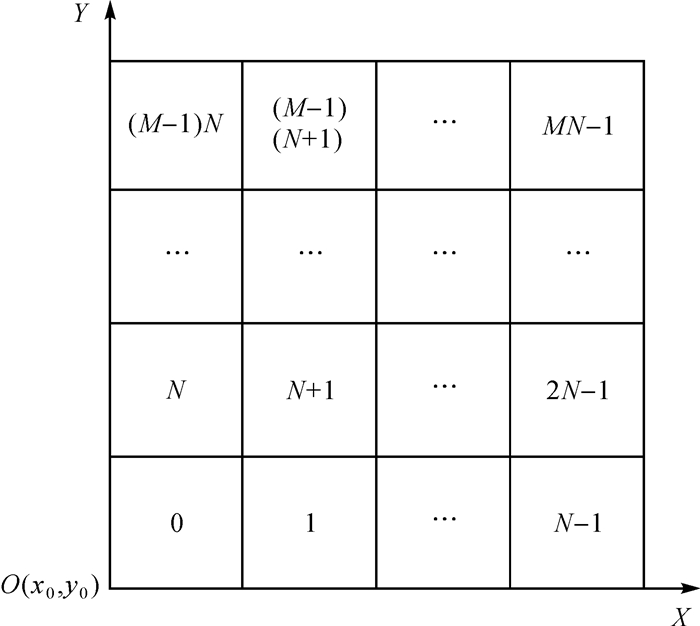
(1) 式中,x0为电子地图最小经度,y0为最小纬度,对应地图坐标点O(x0, y0), 如图 2所示。
|
| 图 2 道路网格划分 |
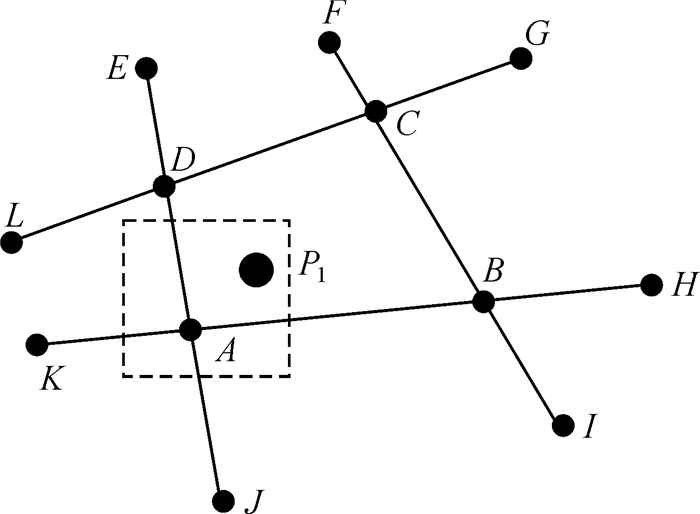
路段的任一点落入编号为j的网格内,则将该路段加入该网格候选路段集Gj中,如图 3所示。
|
| 图 3 候选路段确定 |
由图 3可知,网格j的候选路段集Gji={AB, AD, AK, AG}(i=1, 2, 3, 4),其中i为候选路段集内路段编号。
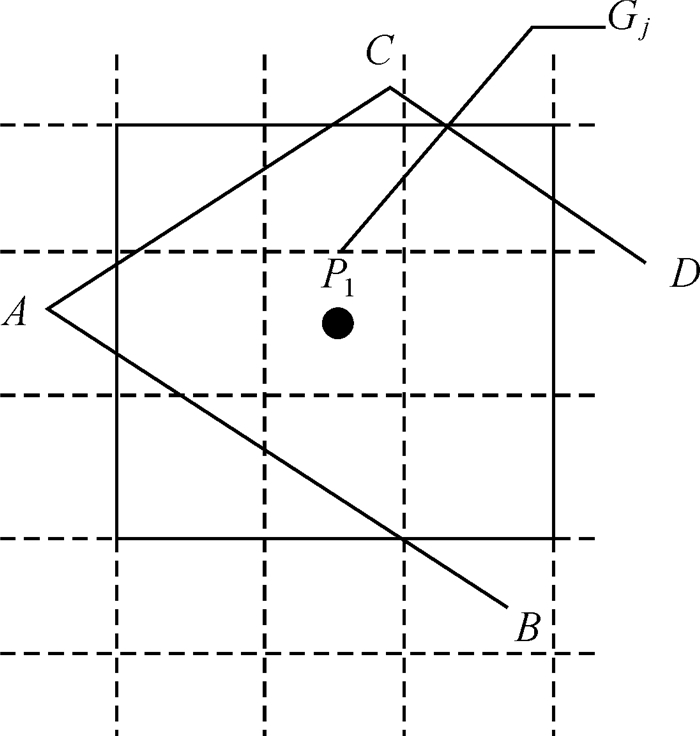
1.1.2 自适应基本网格划分算法基本电子地图网格划分算法,存在空网格即网格内无路段情况,若有初始位置点落入空网格内,如图 4所示,则直接导致匹配错误。针对此问题,本文提出一种改进的自适应网格划分方法,根据网格内路段数动态合并网格。
|
| 图 4 无候选路段网格 |
自适应网格划分算法相关定义如下:
定义1:网格内路段及与网格相交路段构成的集合为该网格路段集,同时为落入该网格内定位点对应候选路段集。
定义2:对应网格路段集为空的网格为空网格。
定义3:合并一次网格指合并空网格周围直接与空网格相接的网格,合成网格编号仍为原空网格编号。
定义4:认定经过两次合并的网格若其对应网格路段集仍为空,则认定该区域为错误区。
自适应网格划分算法基本思想如下:
步骤(1):判断各网格对应网格路段集是否为空,若为空,则标记对应网格为空网格并进行下一步,若不为空则跳到步骤(4)。
步骤(2):对空网格合并一次网格,判断合成网格对应网格路段集是否为空,若数量为空,则标记该网格为空网格并进行下一步,若不为空则跳到步骤(4)。
步骤(3):对空网格合并一次网格,判断合成网格对应网格路段集是否为空,若数量为空,则标记该网格为错误区,若不为空则进行下一步。
步骤(4):确定此路段集为该网格对应网格路段集。
以图 4为例,基本网格划分方法认定网格j网格路段集为空,P1点落入该网格内,对应候选路段集为空,直接导致P1匹配错误。对于自适应网格划分方法,将以网格j为中心合并与该网格直接相接的网格并形成新网格,网格编号仍为j,网格j路段集及P1点候选路段集Gji={AB, AC, CD}(i=1, 2, 3)。
自适应网格划分算法在基本网格划分算法快速高效确定候选路段集基础上,有效解决了空网格问题,在一定程度上提高了匹配准确度,为改进的浮动车地图匹配算法高效精确实现地图匹配过程奠定了基础。
1.2 基于权重的最优匹配路段确定算法低频采样浮动车数据前后定位点间联系性缺失,单个定位点航向偶然性较大,本文算法引入最短路径构建了前后定位点间联系性,引入轨迹方向信息降低了单个定位点的偶然性。由于车辆可能不完全按照最短路径运行,传统的最短距离与航向信息仍被应用到地图匹配过程中。采用基于权重的最优匹配路段确定算法,计算各候选路段权重,包括最短距离权重ZQ、航向差权重CQ、最短路径权重LQ及轨迹方向差权重GQ,并计算总权重W以确定最优匹配路段。
基于权重的最优匹配路段确定算法相关定义如下:
定义5:最短距离指初始定位点到各候选路段的最短距离,最短距离可能是到候选路段垂点距离,也可能是到候选路段端点距离。
定义6:候选匹配点指候选路段上的对应匹配点,是候选路段上到初始定位点距离最短的点,可能是初始定位点在候选路段上垂点,也可能是候选路段端点。
定义7:航向指从车辆定位数据中获取的车辆行驶方向信息,以正北方向为零,航向变化范围是0, 2π。
定义8:候选路段方向是从路网数据中获取的路段方向,以正北方向为零,候选路段方向变化范围是0, 2π。
定义9:最短路径是指上一正确匹配点到当前候选匹配点之间的最短路径。
定义10:轨迹方向是指上一个初始定位点与当前初始定位点之间连线的方向,以正北方向为零,其变化范围是0, 2π。
1.2.1 最短距离权重最短距离权重用ZQ表示,其表达式为
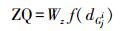 (2)
(2) 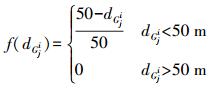 (3)
(3) 式中,Wz为最短距离权重的权重系数;dGji指待匹配点到候选路段的最短距离。最短距离越小,ZQ的权重分数越高。如初始定位点靠近某个候选路段,则这个路段具有更高的可能性是正确匹配路段。
1.2.2 航向差权重航向差是指车辆航向与候选路段方向相比较得到的差值,车辆航向差权重记为CQ, 其表达式为
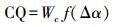 (4)
(4) 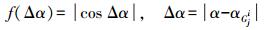 (5)
(5) 式中,Wc为车辆航向差权重的权重系数;α为车辆航向;αGji为候选路段方向角;Δα取值范围为[0, 2π],f(Δα)取值范围为[0, 1]。浮动车GPS数据为低频采样方式,在采样间隔内车辆可以从路段任意方向行驶到采样位置,基于此本文对航向差及其对应余弦值加绝对值处理,相较于文献[7]航向差计算方法降低了计算复杂度,提高了计算效率。
1.2.3 最短路径权重通过前后定位点间最短路径构建联系性,提高匹配准确度。本文采用Dijkstra最短路径搜索算法确定前后定位点间最短路径。Dijkstra算法可搜索一点到其他所有点的最短路径,由于城市路网密度较大,最短路径搜索效率较低。采用文献[1]中缩小搜索范围的方法,根据车辆最大行驶速度vmax与前后定位点间时间差Δt确定最大行驶距离dmax,基于最大行驶距离构建搜索区域
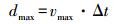 (6)
(6) 搜索区域如图 5所示,其中P1是上一定位点最终匹配点,P2是当待带匹配点。确定最短路径搜索区域,可有效提高最短路径搜索效率。

|
| 图 5 搜索区域 |
最短路径权重用LQ表示,其表达式为
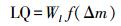 (7)
(7) 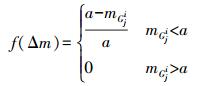 (8)
(8) 式中,Wl为最短路径权重的权重系数;mGji为从上一定位点最终匹配点到当前待匹配点对应各匹配点之间最短路径长度;a为预设阈值,单位为m,a的大小由浮动车数据采样频率决定。最短路径长度越小,LQ的权重分数越高。
1.2.4 轨迹方向权重方向差指轨迹方向与候选路段方向之间差值,轨迹方向权重用GQ表示,其表达式为
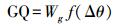 (9)
(9) 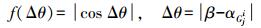 (10)
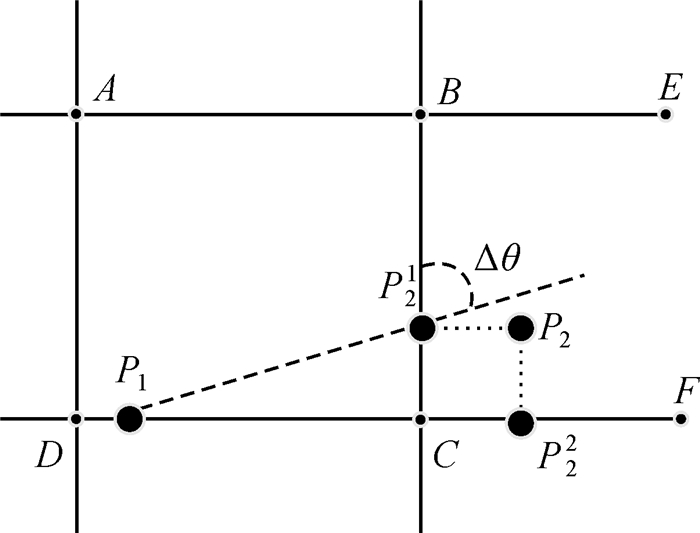
(10) 式中,Wg为轨迹航向权重的权重系数;β为轨迹方向;αGji为候选路段方向。以图 6为例,其中P1为上一定位点最终匹配点,P21与P22分别为当前定位点P2在路段BC与路段CF上的候选匹配点,Δθ为P1与P21之间轨迹方向与候选路段BC方向角的差值,P1与P22之间轨迹方向与对应候选路段CF方向角差值为0,则CF有更高可能性是正确匹配路段。
|
| 图 6 轨迹方向信息 |
轨迹方向与候选路段方向差值越小,则对应的候选匹配点是正确匹配点的可能性就越高。
1.2.5 总权重权重总和为W,其表达式为
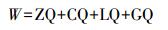 (11)
(11) 根据公式计算每条候选路段的总权重,候选路段当中最高权重的路段被认定为正确匹配路段,在选择路段上的匹配点认定为正确的匹配位置点。
2 试验和验证 2.1 地图数据处理为了验证算法的可行性,本文首先在ArcGIS平台下建立山东省淄博市张店区路网数据,在路网数据中加入路段长度、路段方向及道路线路等信息,进行拓扑处理构建路网拓扑关系,为改进浮动车地图匹配算法提供完善可用的路网数据。选取(117.934, 36.624)作为网格坐标原点,使得张店区在第一象限,取l=50 m划分网格,根据网格内路段数动态合并网格,标记错误区。
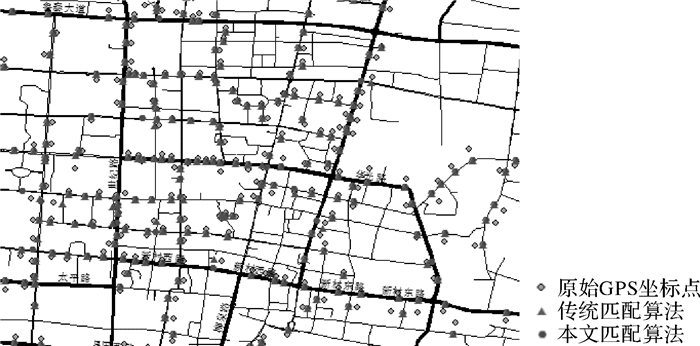
2.2 地图匹配本文试验数据来源于2014年山东省淄博市出租车GPS数据。首先采用某出租车在2014年1月28日8:00:00—21:00:00的GPS数据进行验证,该出租车GPS数据为0.067 Hz的低频采样数据,该时间段内共有670条GPS数据,剔除不在淄博市张店区内的GPS数据及长时间停留GPS数据后,共有438条可用数据。Wz、Wc、Wl、Wg值均设置为0.25。出租车GPS数据初始位置点、传统基于最短距离与航向权重的匹配结果,以及本文匹配结果如图 7所示。
|
| 图 7 初始点与结果对比 |
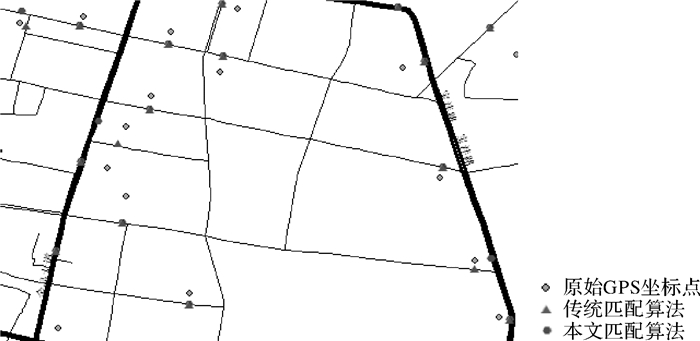
局部匹配结果对比如图 8所示。从图 7和图 8中发现,传统基于最短距离与航向权重的地图匹配算法在匹配处于道路交叉口与平行路段的GPS位置点时易匹配错误,而本文算法在同样情况下有较好匹配效果。
|
| 图 8 局部匹配效果 |
匹配结果对比分析见表 1。
单辆出租车GPS数据匹配结果表明,本文匹配算法在保证匹配效率的情况下提高了匹配准确度,实现了预期目标。
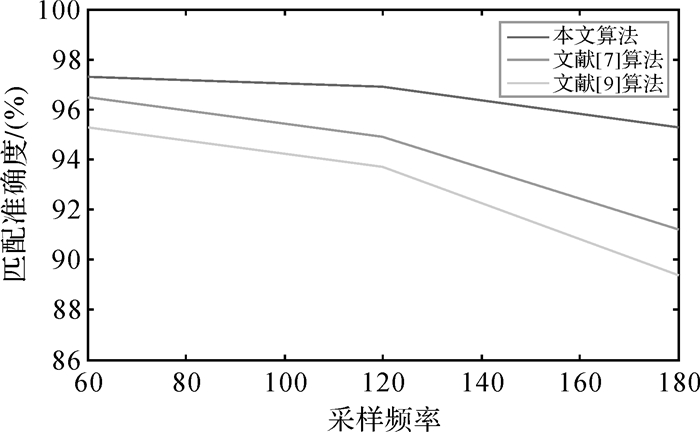
为进一步验证本文算法对低频采样的浮动车数据匹配效果,基于原始数据采样间隔进一步抽稀数据,得到采样间隔为120 s及180 s的出租车GPS定位数据,使用原始定位数据(60 s采样间隔)及抽稀得到的数据(120 s及180 s间隔)验证算法性能,并与文献[7]及文献[9]匹配算法进行对比,试验结果对比分析如图 9所示。
|
| 图 9 不同采样频率匹配对比 |
结果表明,对于60 s间隔的采样数据,各算法均具有较高的匹配准确度,采样频率降低时,各算法匹配准确度均有所下降,但本文算法仍然具有较好的准确度。文献[7]匹配算法在传统基于权重地图匹配算法基础之上加入可达性权重,提高了算法匹配准确度,但可达性对于路网密集区域辨识度不高,且随着采样间隔的增大,车辆航向的偶然性也随之增大,通过最短距离、航向及可达性判断最优匹配路段的难度增加,相应的准确度随之降低。文献[9]采用几何及路网拓扑确定匹配点,当采样间隔增大时,通过此方法很难建立前后定位点间联系,相应匹配难度增加准确度降低。本文算法基于最短路径建立前后定位点间联系性,基于轨迹方向信息弱化单个定位点航向偶然性,在采样间隔增大时,可有效保障匹配的准确性。
为验证本文算法处理海量浮动车数据时的匹配性能,随后选取500~50 000之间不同数量的GPS定位点数据测试算法,单点匹配耗时如图 10所示。

|
| 图 10 单点匹配耗时 |
由图 10可知,随着定位点个数的不断增加,单点匹配耗时略微呈上升趋势,但其耗时仍能满足一般智能交通系统的实时性要求。结果表明,本文匹配算法在处理海量浮动车数据时仍有较高的匹配效率。
本文算法通过改进的自适应网格划分方法快速确定候选路段集,增加最短路径权重和轨迹方向权重辅助地图匹配过程准确确定最优匹配路段,在保证算法运行效率的同时提高了算法匹配准确度。
3 结语针对现有地图匹配算法应用于低频采样的浮动车数据时匹配准确度与匹配效率不能同时兼顾的问题,本文提出了一种改进的浮动车地图匹配算法。基于改进的自适应网格划分算法在高效确定候选路段集的同时有效解决了传统网格化方法的空网格问题,在一定程度上提高了匹配的准确度;基于权重的最优匹配路段确定算法在传统匹配算法中加入最短路径与轨迹方向信息,建立了前后定位点间联系性,削弱了单个定位点航向的偶然性,有效提高了算法的匹配准确度。改进的自适应网格划分算法与基于权重的最优匹配路段确定算法相结合,在保证匹配效率的同时提高了算法的匹配准确度。最短路径信息的引入在一定程度上增加了算法的复杂性,如何进一步降低最短路径搜索时间是本文下一步研究的焦点。
| [1] | 沈敬伟, 周廷刚, 张弘弢. 基于改进AOE网络的低频浮动车数据地图匹配算法[J]. 西南交通大学学报, 2015, 50(3): 497–503. |
| [2] | 李清泉, 黄练. 基于GPS轨迹数据的地图匹配算法[J]. 测绘学报, 2010, 39(2): 207–212. |
| [3] | 赵东保, 刘雪梅, 郭黎. 网格索引支持下的大规模浮动车实时地图匹配方法[J]. 计算机辅助设计与图形学学报, 2014, 26(9): 1550–1556. |
| [4] | 王仁礼, 陈天泽, 王冬红. 智能型地图匹配综合算法的研究[J]. 计算机辅助设计与图形学学报, 2003, 15(11): 1443–1447, 1451. DOI:10.3321/j.issn:1003-9775.2003.11.021 |
| [5] | 周成, 袁家政, 刘宏哲, 等. 智能交通领域中地图匹配算法研究[J]. 计算机科学, 2015, 42(10): 1–6. |
| [6] | WHITE C E, BERNSTEIN D, KORNHAUSER A L. Some Map Matching Algorithms for Personal Navigation Assistants[J]. Transportation Research Part C:Emerging Technologies, 2000, 8(1): 91–108. |
| [7] | 卢文涛, 周银东, 梅顺良, 等. 基于拓扑结构的地图匹配算法研究[J]. 测控技术, 2010, 29(6): 73–76. |
| [8] | CHO Y, CHOI H. Accuracy Enhancement of Position Estimation Using Adaptive Kalman Filter and Map Matching[J]. International Journal of Control and Automation, 2014, 7(7): 167–178. DOI:10.14257/ijca |
| [9] | 苏海滨, 王光政, 王继东. 基于模糊神经网络的地图匹配算法[J]. 北京科技大学学报, 2012, 34(1): 43–47. |
| [10] | YANG D, ZHANG T, LI J, et al. Synthetic Fuzzy Evaluation Method of Trajectory Similarity in Map-matching[J]. Journal of Intelligent Transportation Systems, 2011, 15(4): 193–204. DOI:10.1080/15472450.2011.620478 |
| [11] | 肖维丽, 岳春生, 奚玲. 基于高程的改进D-S证据理论地图匹配算法[J]. 计算机应用与软件, 2015, 32(7): 262–265. |
| [12] | 王美玲, 程林. 浮动车地图匹配算法研究[J]. 测绘学报, 2012, 41(1): 133–138. |
| [13] | 曾喆, 李清泉, 邹海翔, 等. 曲率积分约束的GPS浮动车地图匹配方法[J]. 测绘学报, 2015, 44(10): 1167–1176. |
| [14] | 刘卫宁, 汪杰宇, 郑林江. 基于时空分析的地图匹配算法研究[J]. 计算机应用研究, 2016, 33(8): 2266–2269. |
| [15] | 杨旭华, 彭朋. 基于条件随机场和低采样率浮动车数据的地图匹配算法[J]. 计算机科学, 2016, 43(S1): 68–72. |


