遥感图像分割是一个将图像域划分成具有不同土地利用和土地覆盖(land use and land cover, LULC)类型区域的过程,是实现遥感影像信息自动提取的关键步骤,具有重要意义[1-2]。随着遥感技术的不断发展,遥感图像的空间分辨率不断提高,高空间分辨率遥感图像(下文简称高分遥感图像)具有以下特点:①相对于中低分遥感图像,高分遥感图像在相同地面覆盖面积上的数据量增长了上千倍,呈现海量性的特点;②高分遥感图像蕴含更加丰富的地物几何、纹理、光谱信息,呈现更多的地物细节信息[3]。高分遥感图像这些特点使得地物目标提取方面极具潜力,但也给传统的遥感图像分割方法带来一些新的挑战。高分遥感图像海量性的特点决定了其分割方法必须运行高效,才能满足实际应用需求。在更精细的空间尺度下,地物光谱信息的异质性大大增强,使得图像中大尺度的地物类型,如草地、湖泊、裸地等,受光照、地形等因素的影响呈现局部非均匀性等特点,造成传统分割方法对高分遥感图像分割结果的精度并没有随着空间分辨率的提高而提高[4-6]。
目前针对高分遥感图像的分割问题进行了大量研究,提出了许多基于聚类的算法。其中,模糊C均值(fuzzy C-means, FCM)算法具有原理直观、稳定、收敛速度快等特点且易于扩展[7-8];引入的隶属度能充分刻画光谱测度隶属的不确定性,对低噪声且地物异质性较低的中低空间分辨率遥感图像取得了令人满意的分割结果。但FCM是一种全局最优算法,缺乏局部空间约束,使得该方法无法解决高分遥感图像局部异质性问题。
针对传统分割方法对图像中目标结构复杂性刻画能力不足的问题,国内外一些学者将多主体系统(multi-agent system, MAS)引入图像分割中,并取得了很大进展[9-13],但将MAS用于遥感图像处理的研究不多。Chitsaz等提出一种采用MAS的CT影像的分割方法[14],该方法根据目标的阈值作为先验知识以及两层主体系统(仲裁主体和局部主体)进行类别的划分,对CT影像取得较好的分割结果,但是该方法是一种十分依赖于先验知识的简单图像分割方法,使其难以推广到其他领域的图像分割应用中。张金静等在MAS框架下结合最大期望值和遗传算法提出一种适用于SAR图像的分割方法[15],该方法采用多个分割主体采用EM算法分别对图像进行分割,然后采用协调主体结合遗传算法使分割模型收敛到全局最优,从而得到较为理想的分割结果。但是该算法需要多次对图像执行多次EM算法,并且GA优化过程运行时间太长,使得该方法存在运行时间过长和内存占用很大等问题。MAS是由一系列智能主体通过沟通、协作等机制将复杂任务分散处理的分布式系统框架[16]。因其具有一定的智能性,更适合动态复杂的环境,因此能通过它表达图像中蕴含的丰富信息,结合恰当的数学模型,就可提取出所期望的信息。故将多主体框架引入遥感图像处理中具有一定的应用前景。
针对高分彩色遥感图像的数据海量性和局部非均匀性问题,提出一种MAS框架下基于模糊C均值(FCM)算法的彩色遥感图像分割方法。首先利用规则划分将图像域划分成若干个子块,每个分割主体控制一个子块;然后每个分割主体分别执行初始分割,并与全局分割模型协调子块类别数与标号统一;再利用分割主体邻域协调解决遥感图像局部非均匀性对图像分割的影响,以确定局部聚类中心,从而实现全局最优分割。
1 MAS分割模型 1.1 FCM算法为了实现彩色遥感图像的FCM分割[17],定义模糊隶属度矩阵U={uik|i=1, 2, …, n; k=1, 2, …, K},其中,K为聚类个数,n为图像像素个数,uik为像素i对聚类k的隶属度,且满足条件0≤uik≤1,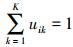
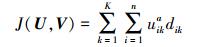 (1)
(1) 式中,a为模糊因子;dik为像素i到聚类中心vk的欧氏距离;V={vk|k=1, 2,…, K}为聚类中心矢量。引入拉普拉斯算子作为式(1)的求极值约束条件,得到模糊隶属度函数为
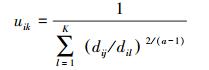 (2)
(2) 则聚类中心函数为
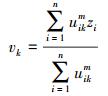 (3)
(3) 通过迭代式(2)和式(3),最小化目标函数,并通过式(4)反模糊化以确定每个像素的类属,从而完成聚类。
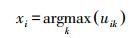 (4)
(4) 根据分割主体需要执行的任务,将涉及FCM分割的过程分为包含子块FCM分割过程和基于模型校正的FCM分割过程两种,为叙述方便,分别用非监督FCM(un-supervised fuzzy C-mean, USFCM)和监督FCM(supervised fuzzy C-mean, SFCM)表示。USFCM分割过程只根据子块类数Kt或全局类数K0进行无监督分类,是完整的FCM执行过程;而SFCM分割过程则根据给定的聚类中心进行的监督分类过程,相比于完整的FCM执行过程,只执行模糊隶属度(式(2))计算和反模糊化(式(4))两个过程,也即只执行给定聚类中心的分割过程。
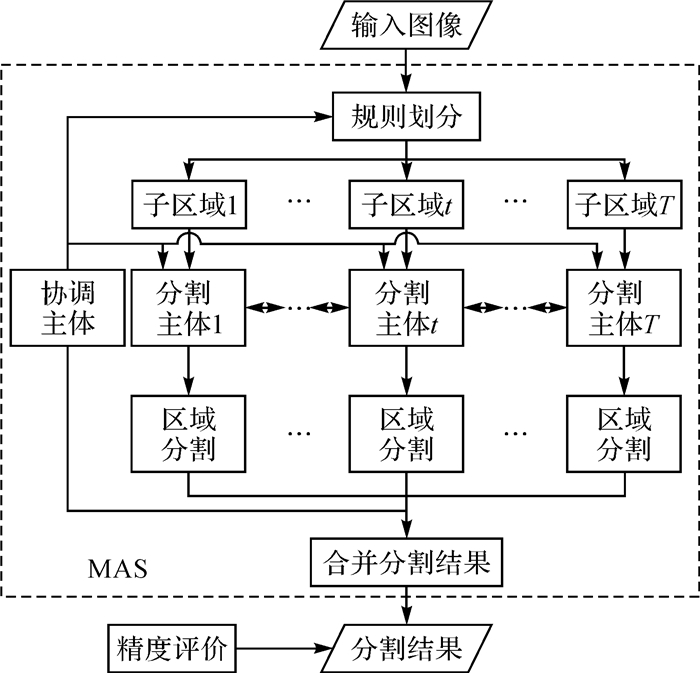
1.2 MAS分割模型为了较好地实现彩色遥感图像分割,提出一种MAS系统,如图 1所示。该系统由T个分割主体和一个协调主体构成。分割主体采用FCM算法对每个子块进行初始分割,然后与其邻域分割主体协作完成对应区域分割。协调主体负责对各个分割主体调度、协调,以实现全局最优分割。MAS系统中协调主体和分割主体形成一种1对多类型的主从式结构,分割主体形成分布式结构且可以并行执行。
|
| 图 1 MAS系统界面 |
设z={zp|p∈P}为定义在图像域P上的彩色遥感图像,为特征场Z={Zp|p∈P}的一个实现,其中,Zp=(ZpR, ZpG, ZpB)为像素p的彩色矢量,p=1, 2, …, n,n为图像像素总数。X0={Xp|p∈P}为定义在P上的全局标号场,Xp∈{1, 2, …, K0}表示像素p的标号变量,K0为图像的全局类别数。
采用规则划分技术,将图像域P按照规则划分成T个大小相等的子块,即P={Pt|t=1, 2, …, T},得到T个分割主体。定义子块Pt的局部标号场为Xt={Xp|p∈Pt},Xp∈{1, 2, …, Kt},Kt为子块Pt的类别总数。
以全局类别数K0为所有子块的类别数,利用USFCM对其进行分割,获取各子块的初始聚类中心Vt={vtk|t=1, 2, …, T; k=1, 2, …, K0}。由于该过程每个子块相互独立,故可并行执行。而有些子块的实际类别数小于K0且各子块分割结果标号不统一,因此,要进行子块类别数的确定及各子块标号的统一。首先,利用USFCM对整幅图像进行分割,得到全局聚类中心V0={v0k|k=1, 2, …, K0},将其作为校正的基准参数。然后,以欧氏距离作为协调主体的相似性测度;对于子块Pt,计算各初始聚类中心与全局聚类中心V0的欧氏距离,选择最小值,将子块中该聚类中心及类别与全局对应,从而确定该子块的类别数Kt;再判断Kt与K0的关系,若Kt < K0,说明初始分割有误,则以Kt为该子块类别数,调用USFCM重新分割,并更新子块聚类中心Vt;若Kt=K0,说明原始分割正确,则无需重新分割。依次类推,遍历所有子块,从而实现各子块类别数的确定及类别的统一。
然后通过分割主体与邻域分割主体进行检验模型和改正模型两个操作来调整各子块的聚类中心。首先,随机选择一子块Pt,激活其对应分割主体At;对于处于激活态的分割主体At,执行模型检验。具体步骤为:在子块Pt内,对于每一类k=1, 2, …, Kt,将分割主体At的聚类中心vtk和方差σtk2作为局部模型,并将邻域主体中所有含有类别为k的像素的平均聚类中心vtk和方差σtk2作为局部平均模型。则两个模型之间的Kullback-Leibler(KL)距离Dtk定义为
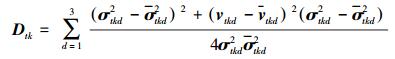 (7)
(7) 对于给定阈值εkeep和εreplace(εkeep < εreplace),模型改正方案如下:
(1) 若Dtk≤εkeep,则局部模型正确,无需改正。
(2) 若Dtk≥εreplace,则将局部平均模型作为局部模型。
(3) 若εkeep < Dtk < εreplace,则改正模型为
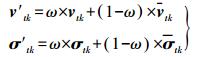 (8)
(8) 式中
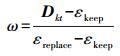 (9)
(9) 完成邻域协作后,如果模型需要改正,该分割主体执行SFCM操作,以重新实现其分割。
1.3 算法流程在MAS框架下,首先将图像域规则划分成大小相等的子块,然后每个分割主体采用FCM算法对其作用范围内的子块进行分割,并与全局模型协作确定子块的类数和标号,协调主体通过协调和激活机制统一各子块聚类中心,实现全局最优分割。具体流程如下:
(1) 初始化协调主体,给定全局类别数K0,采用FCM算法对整个图像域聚类,得到全局模型V0。
(2) 协调主体将图像域划分为T个子块,形成T个分割主体。
(3) 协调主体调用各个分割主体采用FCM进行聚类,得到局部模型Vt, t=1, 2,…, T。
(4) 协调主体通过各分割主体与全局模型协调各个局部主体的类数和标号。
(5) 协调主体随机选择一个子块,激活该分割主体。
(6) 对于处于激活态的分割主体,执行模型检验。若模型需要改正,则按改正方案校验激活态主体的局部模型,并执行SFCM算法;否则执行步骤(7)。
(7) 激活一个未被处理的邻域分割主体,返回步骤(6),直至遍历所有子块。
2 试验结果和讨论为了验证提出方法的有效性和可行性,采用提出算法分别对合成彩色遥感图像和QuickBird遥感图像进行分割试验。
2.1 合成彩色遥感图像以图 2(a)为几何模板生成合成彩色遥感图像,如图 2(b)所示。合成彩色遥感图像包含5类,编号Ⅰ~Ⅴ代表不同的同质区域,而且每个区域的数据均来自QuickBird遥感影像,对应于遥感影像的一类目标,图像的大小为512×512。合成图像中每个区域的目标均表现出局部特征的不一致性,尤其是第Ⅴ个区域最为明显,且第Ⅳ、Ⅴ区域的部分局部彩色特征相近。

|
| 图 2 合成彩色遥感图像 |
为了确定合适的分割主体数,采用规则划分技术,分别将图像域划分成不同子块大小。利用提出算法对合成彩色遥感图像进行分割,图 3为不同子块对应的分割结果。图 3(a)中子块尺寸为256×256,分割主体个数为4;图 3(b)子块大小64×64,分割主体个数为64;图 3(c)中子块大小32×32,分割主体个数为256;图 3(b)子块大小16×16,分割主体个数为1024。比较四幅分割结果的区域Ⅰ,随着子块尺寸的减小,同质区域误分像素逐渐减少;区域Ⅱ也具有相同的特点,当子块大小16×16时,该区域误分像素最少,只有与区域Ⅰ交界处有少量噪声。通过观察区域Ⅲ,发现前三幅结果满足规律,但图 4(d)分割结果没有预期得好,说明该子块过小,而子块内噪声像素过多导致误分。区域Ⅳ和Ⅴ,同样满足子块越小分割效果越好的规律。主体的数量越多,协作的能力越强,越能够消除非均匀性引起的分割困难。因此,提出算法不仅能够自动确定子块中类别数,还能够较好地实现分割。

|
| 图 3 分割结果 |

|
| 图 4 算法比较 |
为了验证提出算法的优越性,选择FCM算法对整幅合成彩色遥感图像(图 2(b))进行对比试验,图 4(a)为采用提出方法分割得到的最优结果,图 4(b)为采用FCM算法分割得到的结果。从视觉上对分割结果进行定性评价,通过与图 2(a)比较发现,图 2(b)中区域Ⅴ大部分误分成第4类,而且其他区域都有很多的误分像素;而图 4(a)同质区域内误分像素很少,很好地将5个区域区分开。因此,提出的方法更加有效。为了定量评价FCM算法与提出算法的分割结果,以模拟图像模板图 2(a)为标准分割数据,求FCM算法与提出算法分割结果的混淆矩阵,并根据此矩阵分别计算出两种算法的用户精度、产品精度、总精度及kappa系数,如表 1所示,表中用正斜杠依次隔开FCM算法与提出算法的计算结果。混淆矩阵的对角线表示分割正确的像素数,从中可以看出分割图像中被误分的像素非常少。从表 1中可以看出采用FCM的第Ⅳ、Ⅴ区域的分割精度不高,第Ⅳ区域的产品精度只有0.62,即有大量的第Ⅴ区域的像素被误分到第4类,而第5类的用户精度只有0.15,即区域Ⅴ中的大量像素被误分到第4类,这也导致了FCM算法的全局精度和kappa系数偏低。而提出方法分割的结果各项精度指标均达到97%以上,总精度为99%,kappa系数达到0.98,达到了优质分类器的指标。究其本质,FCM是特征空间的全局最优算法,由于Ⅴ区域的部分局部特征全局上更接近于第4类,从而导致了大量的区域Ⅴ的像素被误分为第4类;而本文算法通过邻域协调过程,解决了FCM由于局部特征的不一致造成的误分现象。通过对分割结果的定量评价,验证了提出方法能够有效分割大尺度遥感图像。
| 区域 | 类别 | 合计 | 产品精度/(%) | ||||
| 1 | 2 | 3 | 4 | 5 | |||
| Ⅰ | 51 756/52 232 | 0/0 | 0/0 | 0/1 | 17/56 | 51 773/52 289 | 0.99/0.99 |
| Ⅱ | 127/0 | 51 819/52 644 | 16/0 | 2008/39 | 1094/13 | 55 064/52 696 | 0.94/0.99 |
| Ⅲ | 33/0 | 1207/1136 | 72 846/72 864 | 0/0 | 24/156 | 74 110/74 156 | 0.98/0.98 |
| Ⅳ | 289/308 | 1139/396 | 2/0 | 46 499/48 524 | 27 649/511 | 75 578/49 739 | 0.62/0.97 |
| Ⅴ | 335/0 | 11/0 | 0/0 | 57/0 | 5216/33 264 | 5619/33 264 | 0.93/1 |
| 合计 | 52 540 | 54 176 | 72 864 | 48 564 | 34 000 | 262 144 | |
| 用户精度/(%) | 0.98/0.99 | 0.96/0.97 | 0.99/1 | 0.95/0.99 | 0.15/0.97 | ||
| kappa | 0.84/0.98 | 总精度 | 0.87/0.99 | ||||
图 5(a)为QuickBird卫星巴林地区Mina Salman港口的遥感图像,分辨率为0.65 m,图像大小512×512,目视判读其类别数为3,分别为深海、浅海和港口。图 5(b)为QuickBird卫星关岛高尔夫度假村的遥感图像,分辨率0.65 m,图像大小512×512,目视判读其类别数为3,分别为林地、草地和建筑物。

|
| 图 5 真实彩色遥感图像 |
首先将图像分别划分为2×2、8×8、16×16、32×32个子块,分割主体的个数等于子块个数,并采用提出方法分别对图 5中两幅遥感图像进行分割试验。图 6为提出方法的分割结果。图 6(a)—(d)为提出算法对港口遥感图像的分割结果,子块尺度分别为256×256、64×64、32×32、16×16个像素。比较4幅分割结果,图 6(a)中浅海区域分割效果较好,图 6(c)中的深海区分割结果较好,图 6(c)中的港口区分割结果较好。图 6(e)—(h)为提出算法对度假村地区遥感图像的分割结果,可以看出图 6(h)的分割效果最佳。由此发现,分割主体个数越多,同质区域内的噪声越少。随着分割主体个数的增加,主体间的协调过程增多,能够利用的局部信息也增多,因此能够消除分割结果的局部非均匀性。综上所述,对于同一幅图像,分割结果的好坏与分割主体的个数有着直接关联。受局部非均匀性的干扰,子块越大分割效果越不好,子块越小越能够得到好的局部分割结构,但前提是子块的尺度足以支持正确模型参数的估计。经过大量试验发现,当子块尺度为16×16时,提出方法的分割结果最好。

|
| 图 6 分割结果 |
选择FCM算法对真实彩色遥感图像进行分割试验,并将分割结果与提出算法进行对比。如图 7所示,图 7(a)和(c)为采用提出算法的分割结果,图 7(b)和(d)为FCM算法分割结果。对比图 7(a)和(b)发现图右下角区域提出算法分割结果没有误分像素;对比图 7(c)和(d),FCM算法分割结果中林地、草地及建筑物中均有很多误分像素,随机分布在分割区域中,而提出算法较好地消除了误分像素。由此可见,本文提出的算法比FCM算法在真实彩色遥感图像分割中更有优势。

|
| 图 7 算法比较 |
针对彩色遥感图像中数据海量性和局部非均匀性问题,提出一种MAS框架下基于FCM算法的遥感图像分割方法。由于遥感图像数据量大,提出方法利用区域划分将图像分散处理,加快了图像处理速度。利用主体之间协作,解决了遥感图像非均匀性问题。在未来的工作中,将其他几何划分方法与不同的分割算法相结合,以进一步完善主体间的协作机制,使基于MAS的遥感图像分割方法具有更广泛的适用性。
| [1] | YU L. Remotely Sensed Data Segmentation Under a Spatial Statistics Framework[D]. Waterloo: University of Waterloo, 2009. http://hdl.handle.net/10012/4931 |
| [2] | 王玉, 李玉, 赵泉华. 基于规则划分和RJMCMC的可变类图像分割[J]. 仪器仪表学报, 2015, 36(6): 1388–1396. |
| [3] | 李德仁, 童庆禧, 李荣兴, 等. 高分辨率对地观测的若干前沿科学问题[J]. 中国科学(地球科学), 2012, 42(6): 805–813. |
| [4] | BENEDIKTSSON J A, CHANUSSOT J, MOON W M. Very High-resolution Remote Sensing:Challenges and Opportunities[J]. Proceedings of the IEEE, 2012, 100(6): 1907–1910. DOI:10.1109/JPROC.2012.2190811 |
| [5] | BRUZZONE L, CARLIN L. A Multilevel Context-based System for Classification of very High Spatial Resolution Images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(9): 2587–2600. DOI:10.1109/TGRS.2006.875360 |
| [6] | 王春艳, 徐爱功, 杨本臣, 等. 基于区间二型模糊模型的高分辨率遥感影像分割方法[J]. 仪器仪表学报, 2016, 37(3): 658–666. |
| [7] | 赵雪梅, 李玉, 赵泉华. 结合高斯回归模型和隐马尔可夫随机场的模糊聚类图像分割[J]. 电子与信息学报, 2014, 36(11): 2730–2736. |
| [8] | 霍冠英, 刘静, 李庆武, 等. 空间约束FCM与MRF结合的侧扫声呐图像分割算法[J]. 仪器仪表学报, 2017, 38(1): 226–235. |
| [9] | 程显毅, 梁军, 马首明. 基于多agent系统的医学图像进化分割算法的研究[J]. 南京大学学报(自然科学), 2008, 44(5): 503–511. |
| [10] | DUSCHESNAY E, MONTOIS J J, JACQUELET Y. Cooperative Agents Society Organized as an Irregular Pyramid:a Mammography Segmentation Application[J]. Pattern Recognition Letters, 2003, 24(14): 2435–2445. DOI:10.1016/S0167-8655(03)00077-1 |
| [11] | RODIN V, BENZINOU A, GUILLAUD A, et al. An Immune Oriented Multi-agent System for Biological Image Processing[J]. Pattern Recognition, 2004, 37(4): 631–645. DOI:10.1016/j.patcog.2003.09.014 |
| [12] | KASAIEZADEH A, KHAJEPOUR A. Multi-agent Stochastic Level Set Method in Image Segmentation[J]. Computer Vision and Image Understanding, 2013, 117(9): 1147–1162. DOI:10.1016/j.cviu.2013.04.008 |
| [13] | XU X, ZHONG Y F, ZHANG L P. Adaptive Subpixel Mapping Based on a Multiagent System for Remote-sensing Imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(2): 787–804. DOI:10.1109/TGRS.2013.2244095 |
| [14] | CHITSAZ M, SENG W C. Medical Image Segmentation Using a Multi-agent System Approach[J]. The International Arab Journal of Information Technology, 2013, 10(3): 222–229. |
| [15] | 张金静, 李玉, 赵泉华. 多主体框架下结合最大期望值和遗传算法的SAR图像分割[J]. 中国图象图形学报, 2016, 21(1): 86–94. DOI:10.11834/jig.20160111 |
| [16] | MELKEMI K E, BATOUCHE M, FOUFOU S. Chaotic Multiagent System Approach for MRF-based Image Segmentation[C]//Proceedings of the 4th International Symposium on Image and Signal Processing and Analysis. Eagreb: IEEE, 2005: 268-273. http://www.researchgate.net/publication/4181170_Chaotic_MultiAgent_system_approach_for_MRF-based_image_segmentation?_sg=6gkpCyiLsxyUTiQ1-rz4A80VCVelXR2_hqW_2JhfceSJp_g95RRdd82zooZVQIWhYw7B9h6_Qx9b83Gm3iA1Qw |
| [17] | 赵泉华, 李红莹, 李玉. 区域化模糊C均值高分辨率彩色遥感影像分割方法[J]. 控制与决策, 2015, 30(9): 1706–1710. |


