2. 中国科学院地理科学与资源研究所资源与环境信息系统国家重点实验室, 北京 100101
2. State Key Laboratory of Resources and Environmental Information System, Institute of Geographical Sciences and Natural Resources Research, Chinese Academy of Sciences, Beijing 100101, China
人类的出行活动造就了城市的动态性。城市中移动对象(人或车辆)的位置变化感知了城市的韵律,是城市动态性的直接体现[1-2]。随着城市的急剧扩张,以及人类活动空间频度和广度的不断拓展,人类的出行活动引发了一系列的社会问题,如交通拥堵、能耗增加、空气污染等,这些问题影响着人类的生活质量,也一直是城市管理亟待解决的问题。出行活动在带来一系列问题的同时,出行所产生的轨迹数据也为解决这些问题提供了新的契机。出行轨迹的获取随着物联网和智能移动设备的普及而更加便捷[3-4],由此从这些轨迹(出租车轨迹、公卡刷卡、手机定位、社交网站签到等数据)数据中挖掘人类活动信息和活动规律从而探求深层次的移动模式的研究已经广泛开展[5-6]。基于相似性的空间聚类是挖掘轨迹隐含的语义信息的重要方法[7],它通过分析轨迹数据的时间、空间和其他属性信息,将相似的数据聚集在一个类簇中,从而发现一些有意义的信息。如发现人类的移动模式[8]、城市的不同功能分区[9]、兴趣点和兴趣区域的分布[10-11]等,从而为解决城市问题提供直接的、实时的数据与方法支持。
1 移动轨迹模型轨迹数据是一组带有时间戳并按时间排序的离散点序列。对移动轨迹数据进行挖掘之前,必须要对其模型进行定义,根据轨迹模型的定义,来确定轨迹的相似性度量的衡量标准,从而基于轨迹的相似性对对象进行聚类,进一步挖掘数据的语义信息。本文将不同的移动轨迹数据总结为两种模型:轨迹点模型与轨迹段模型。
1.1 轨迹点模型移动对象经过事件触发记录下来的轨迹,或只能反映出行流的轨迹可以用轨迹点模型来表达。轨迹点模型可以表示为
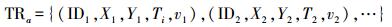 (1)
(1)  (2)
(2) 式(1)表示常规的轨迹点模型。其中,IDi是轨迹点的唯一标识;(Xi, Yi)是轨迹点在二维平面上的坐标;Ti是轨迹点记录的时刻;vi是移动对象的其他属性。式(2)表示OD流模型,模型中的一些参数与式(1)中的相同,Oi和Di分别表示出行流的起始点与终点的坐标。
手机通话数据、WiFi热点数据、社交网络签到数据和公共交通数据(公交卡刷卡、地铁和公共自行车)等都可以看作是轨迹点模型。该类数据粒度较粗,不能直接反映人类活动的真实轨迹,但能反映人类频繁活动或到访的区域。其中,手机通话数据是基于基站产生的轨迹数据,该类数据的位置点是手机所在的基站位置,数据的精度取决于基站的密度;社交网络签到数据为签到点的位置数据,往往包含着很强的语义信息;公交交通数据是上下车的位置数据,能很好地反映OD流。该类轨迹数据主要应用于城市职住地分析[12-13]、个体活动规律[14]、城市空间结构发现[15]等方面的研究。
1.2 轨迹段模型轨迹段是指通过两个轨迹点之间的线性插值得到的轨迹段,轨迹段模型可以表示为
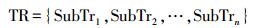 (3)
(3) 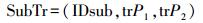 (4)
(4) 式(3)表示移动对象的一条整轨迹,其由许多子轨迹SubTr组成。式(4)中trP1和trP2表示两个相邻的轨迹点。子轨迹段就是由两个相邻轨迹点之间进行线性插值得到的。
由GPS终端采集的频率较高的定位数据得到的轨迹数据可以用轨迹段模型来表达。该类数据具有固定的时间间隔,定位精度较高,如出租车轨迹数据,该类轨迹数据通常受限于道路交通路网[16]。通过对该类数据的挖掘可以实时获取城市交通状况,如车速、车流量等反映交通拥堵状态的信息[17];还可以发现城市热点与预测未来的活动热点等[18]。
2 时空相似性度量相似性度量标准是对数据进行聚类的基础,通过相似性度量来确定轨迹点或轨迹段之间的关系,再对轨迹进行聚类分析。最终得到的结果,是簇内相似度尽可能大,簇间相似度尽可能小。因此,需要定义一个轨迹间的相似度衡量标准。对于轨迹点模型,可以根据数据特点和具体分析的需求定义一种距离函数,然后再根据传统的聚类方法进行聚类。对于轨迹段模型,相似度衡量标准较为复杂,需要判断各轨迹段在时空上的相似性。下面从空间相似性、时间相似性和时空相似性来说明轨迹点模型和轨迹段模型的相似性衡量标准。
2.1 空间相似性度量对于轨迹点模型而言,空间相似性就是指空间距离函数(欧氏距离和路网距离)。空间距离函数如下
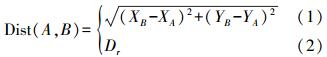 (5)
(5) 式中,(1)表示轨迹点A、B之间的欧氏距离;(2)表示路网距离。
两条轨迹的空间相似性,是由相同子轨迹段所占比例来确定的两条轨迹TR1和TR2(如图 1所示),分别表示为[19]
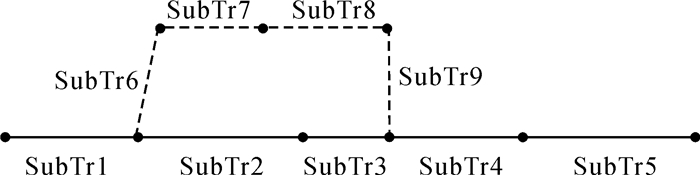
|
| 图 1 轨迹段模型 |
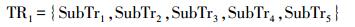 (6)
(6) 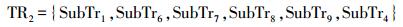 (7)
(7) 两条轨迹的空间相似性,可以用重叠部分的轨迹段的累加长度与整条轨迹长度的比值来表示
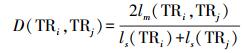 (8)
(8) 式中,lm(TRi, TRj)表示相似轨迹段的长度;ls(TRi)和ls(TRj)分别表示轨迹i和j的总长度。由式(8)可以看出D(TRi, TRj)的取值在[0, 1],0表示两条轨迹完全不相似,1表示两条轨迹完全相似。
2.2 时空相似性度量仅仅考虑空间距离对对象进行聚类划分是不够的,时间是影响聚类结果的另一个因素。如一个区域的聚集程度在上午和晚上肯定是不同的,其反映的真实语义也是不同的。因此,需要利用时间属性来对聚类结果进行过滤。
对于轨迹段模型,时间相似性度量计算公式与式(8)一致,差别在于识别两个轨迹段的重合依据是时间段。
两条轨迹的时空相似性度量可以表示为
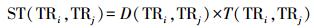 (9)
(9) 式中,ST(TRi, TRj)的取值在[0, 1],0表示完全不相似,1表示完全相似。
3 移动轨迹聚类算法聚类是一种非监督式学习方法,基于相似性将对象聚集成不同的类簇或子集,使同一个类簇中的对象都具有相似的属性[20]。可以通过聚类算法来识别用户感兴趣的地点和区域、发现异常事件、挖掘轨迹中的序列特征等[21]。
根据轨迹数据模型的不同,选择相应相似度衡量标准,进而选用合适的聚类方法。对于轨迹点模型,以距离函数作为相似度衡量标准,聚类思想与传统的聚类方法相同。轨迹段模型要以整条轨迹的时空相似性度量标准来进行聚类分析,具体的聚类方法要与传统的方法有所不同。
3.1 传统的聚类方法常见的有4种方法:划分方法、层次方法、基于密度的方法和基于网络的方法[22]。
3.1.1 划分方法划分方法是将对象集合划分成k份,每一个划分表示一个聚类[23]。一般的,以所得到的聚类使得客观划分标准(即相似函数,如几何距离等)最优化来达到较好的划分效果,使结果满足:①每个聚类簇至少包含一个数据对象(不能有空的簇);②每个数据对象只能属于一个聚类簇(任意两个聚类簇交集为空);③使准则函数(方差之和)达到最小值(式(5))。衡量划分结果的准则为:尽可能地使同一类簇(划分)之间的数据差异最小,不同类簇(划分)之间的数据差异最大。
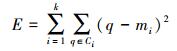 (10)
(10) 式中,k表示聚类簇的个数;q表示聚类簇Ci中的所包含的数据对象;mi表示聚类簇Ci的中心点(均值)。
常用的算法包括K-Means[24]、K-Medoids[25]和EM算法[26]等,这些启发式算法适合于发现中小规模数据集中的球状簇。Mohamed等提出了一种适用于移动对象轨迹数据聚类的新的K-Means算法,该算法根据移动对象的移动方向、加速度和时间间隔,来确定算法中的聚类数k值,克服了K-Means算法对初始值依赖的缺点[27]。Park等在K-Means基础上进行了改进,提出了K-Medoids算法,该算法用各聚类的中心点作为参考点,克服了K-Means算法对异常值敏感的缺陷[28]。何彬彬等考虑空间聚类的随机性和不确定性,基于EM算法和空间对象的Delaunay三角网的邻近关系,提出了不确定性的空间聚类算法[29]。
3.1.2 层次方法层次方法是将数据以树的形式分成若干组,表现形式有两种:一种是自下而上凝聚层次的聚类方法(AGNES),另一种是自顶而下分解层次的聚类方法(DIANA)[30],如图 2所示。层次聚类算法能产生高质量的聚类,但存在计算和存储需求大,且缺乏全局目标函数等缺点。层次聚类方法的主要代表算法有BIRCH[31]、CURE[32]和ROCK[33]等。Tu等提出了一种基于BIRCH算法的在线分隔时间序列数据的方法,该方法很容易发现时间序列模式的变化,时间复杂度也较低,能够取得更好的分割效果[34]。Shao等提出了一种基于改进的CURE算法的大规模网络文本数据聚类算法,CURE算法在大数据集中有较好的伸缩性,因此在大型数据挖掘中应用广泛[35]。
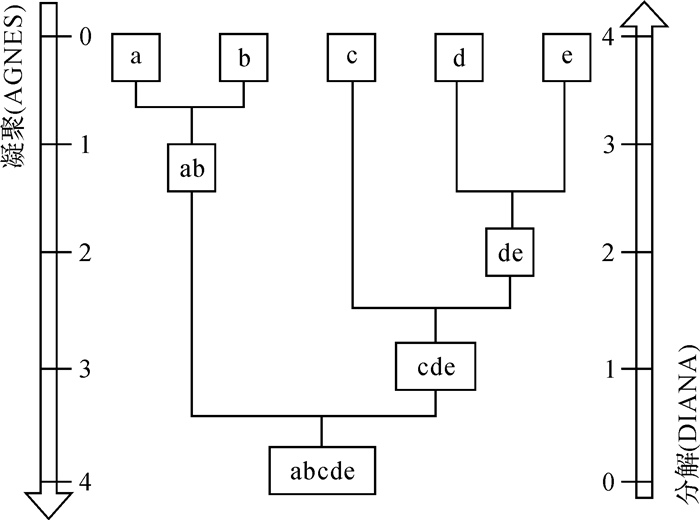
|
| 图 2 凝聚和分解层次聚类方法示意图 |
基于密度聚类的思想主要是:对于样本中的每个数据点,在一个给定范围的区域(ε)中至少包含某个数量(MinPs)的点[36]。与基于层次聚类和划分聚类的凸形聚类簇不同,该算法可以发现任意形状的聚类簇,而且还可以过滤“噪声”孤立点。基于密度聚类的方法主要有DBSCAN算法[37]和OPTICS算法[38]。DBSCAN算法在进行聚类时需要设置初始参数ε和MinPs,为了解决这一问题,Ankerst等提出了OPTICS算法,它是一个自动和交互式的聚类方法,该算法不产生明确的数据聚类,而是创建一个基于密度的聚类结构的数据库,其中包含了很多满足需求的簇序列[40]。Schoier等提出了一种改进的DBSCAN算法,该算法以Lagrange-Chebychev度量作为相似度指标,来发现较大空间数据集的单元簇,对于高维较大空间数据集的执行效率也较高[39]。Huang等提出了一种基于网格和基于密度的混合聚类算法GRPDBSCAN,该算法可以有效处理噪声点,运行效率比传统基于密度的聚类算法要高,并且可以自动地生成ε和MinPs两个参数[40]。
3.1.4 基于网格的方法基于网格的方法把对象空间划分为有限数量的单元,从而形成一个网络布局,所有的聚类操作都在量化的空间结构上进行[41-42]。该方法的优点在于处理速度比较快,而且它的处理时间独立于数据对象的数量,只和量化空间中每一维的单元数量有关。基于网格的聚类方法的一个难点在于网格大小的选取,Edla等通过使用类簇的边界来寻找最佳网格粒度的大小[40]。基于网格聚类的算法有STING和CLIQUE等。STING算法是一种基于网格的多分辨率聚类技术,该算法有利于并行化处理,处理效率很高[43]。CLIQUE算法是基于网络和基于密度聚类方法的结合,适用于高维数据的聚类[44]。
3.1.5 其他聚类方法邓敏等为了改善传统聚类算法对输入参数的依赖,提出了一种基于场论的空间聚类方法(FTSC),该算法通过使用Delaunay三角网来表示实体间的邻近程度,因此算法不涉及输入参数的设置,并且可以发现任意形状的簇,具有较强的鲁棒性[45]。Izakian等提出了一种自动化模糊聚类粒子群优化技术来发现移动轨迹数据的结构特征,粒子群优化方法主要用来找到最优聚类簇数量及最佳聚类中心,从而提高算法的性能[46]。Li等基于层次聚类的思想提出了一种移动微聚类算法(moving micro-clustering,MMC),并应用在移动轨迹数据的聚类中[47]。
表 1给出了基于几何聚类的几种传统算法各自的优缺点。
| 聚类方法 | 算法代表 | 优点 | 缺点 |
| 划分方法 | K-Means、K-Medoids、EM算法 | 对于较大的数据集,具有相对可伸缩性和高效性 | 必须事先定义好k值(要生成簇的数量),不识别噪声,凸形和球形限制 |
| 层次方法 | BIRCH、CURE | 适用于任意聚类形状和属性的数据集,能灵活控制不同聚类层次[48] | 大大延长算法时间,不能回溯处理,算法终止条件很难确定 |
| 基于密度的方法 | DBSCAN、OPTICS | 根据密度来划分聚类,可以有效地监测异常数据,构建任意形状的簇 | 参数需要提前定义,通过大量的试验才能确定更好的参数 |
| 基于网格的聚类方法 | STING、CLIQUE | 处理时间与数据对象的数量及数据的输入顺序无关,可以处理任意类型的数据 | 聚类质量过度依赖于划分网格的单元,某一程度上影响了聚类的质量和准确性 |
基于道路网络空间的聚类,即道路约束下的聚类,属于障碍空间下的聚类[49]。该类聚类方法适用于受限于道路网络的连续型轨迹数据,如车辆轨迹数据等。Liu等提出了一种在道路网络约束条件下的聚类对象模型,给出了约束聚类算法,并验证了算法的效率[50]。廖律超等结合移动对象的方向信息提出了一种有向密度的快速聚类方法,来提取城市复杂路网的结构信息[51]。实际上,该类聚类方法是基于几何空间聚类思想的扩展和细化,它更侧重于通过交通流及流密度来反映移动对象的特性。基于道路网络空间聚类,主要在于动态微观现象的发现,以及城市细粒度现象的发现。
为了得到移动对象在某一聚集的时间段内高流量、强连续的运动轨迹,通常采用轨迹段模型。轨迹段模型聚类以时空相似性来衡量两条轨迹段是否相似,需要考虑移动对象的速度、方向和位置[52]。轨迹段的聚类可以分为两类:移动对象的轨迹段聚类和道路路段划分聚类。
3.2.1 移动对象的轨迹段聚类马林兵等将时空轨迹数据进行离散化处理,利用CLIQUE算法对离散化后的轨迹段进行聚类分析[53]。Lee等提出了一种新的轨迹聚类的划分-组合(partition-and-group)框架,通过把轨迹划分成轨迹片段的集合,再把轨迹片段聚集到簇中,基于这种划分组合框架提出了一个轨迹聚类的算法TRACLUS[54],如图 3所示。
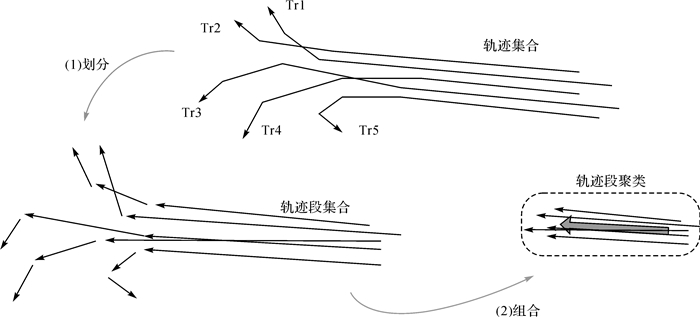
|
| 图 3 轨迹段聚类划分-组合框架 |
道路路段划分聚类的主要思想:①道路交叉口被看作初始划分点,将道路划分成道路片段;②对应于每个道路段的轨迹段可以看作是一个局部聚类簇;③轨迹段需要在道路交通流连续的基础上聚类。Han等提出了一种道路网络感知的方法(NEAT)进行轨迹数据聚类,来发现一组高密集、高度连续的移动对象的交通流子轨迹[55],如图 4所示。
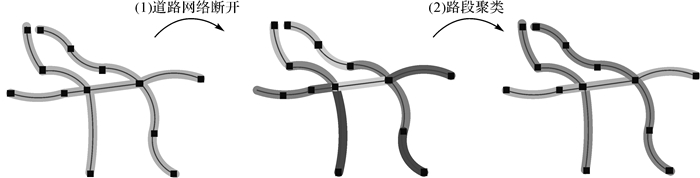
|
| 图 4 道路路段划分聚类框架 |
移动轨迹数据作为社会感知位置大数据的重要表现形式,蕴含了人类活动的时空规律,表征着城市的脉搏和动态。通过对这些数据的挖掘和分析,能及时有效地发现人群移动规律、探测城市热点区域、感知实时交通状态、挖掘城市功能分区等,能真实反映城市的韵律,是城市计算的主要数据源,为解决城市问题提供了科学的数据支撑。聚类是对这些数据进行挖掘和分析的重要方法,也是为进一步研究进行数据处理的基础环节。本文根据不同的轨迹模型定义不同的相似度衡量标准,进一步对两类轨迹模型的聚类方法进行了详细的描述,得出聚类方法的关键在于相似度衡量标准的确定。
移动轨迹数据聚类方法尽管已经有广泛的研究,但仍然存在一些挑战,具体体现在以下几个方面:①对于不同结构的数据,如何准确判断数据之间的相似性衡量指标,以使聚类方法适合于广泛存在的异构数据;②对于需要设置初始参数的聚类算法,怎样才能更准确地设置参数,或实现自适应的聚类方法;③聚类结果的有效性评价一直是时空聚类分析中的难点问题,移动轨迹数据聚类的有效性评价需要更加深入,如何使现有的聚类方法适应动态轨迹数据也需要进一步研究。
| [1] | 牟乃夏, 张恒才, 陈洁, 等. 轨迹数据挖掘城市应用研究综述[J]. 地球信息科学学报, 2015, 17(10): 1136–1142. |
| [2] | 李石坚, 齐观德, 张王晟. 移动轨迹数据分析与智慧城市[J]. 中国计算机学会通讯, 2012, 8(5): 31–37. |
| [3] | 李清泉, 李德仁. 大数据GIS[J]. 武汉大学学报(信息科学版), 2014, 39(6): 641–644. |
| [4] | 郑宇. 城市计算概述[J]. 武汉大学学报(信息科学版), 2015, 40(1): 1–13. |
| [5] | YE Y, ZHENG Y, CHEN Y, et al. Mining Individual Life Pattern Based on Location History[C]//Tenth International Conference on Mobile Data Management: Systems. Taipei: [s. n. ], 2009. http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=5088915 |
| [6] | 刘瑜, 康朝贵, 王法辉. 大数据驱动的人类移动模式和模型研究[J]. 武汉大学学报(信息科学版), 2014, 39(6): 660–666. |
| [7] | 龚玺, 裴韬, 孙嘉, 等. 时空轨迹聚类方法研究进展[J]. 地理科学进展, 2011, 30(5): 522–534. DOI:10.11820/dlkxjz.2011.05.002 |
| [8] | 刘瑜, 肖昱, 高松, 等. 基于位置感知设备的人类移动研究综述[J]. 地理与地理信息科学, 2011, 27(4): 8–13. |
| [9] | YUAN J, ZHENG Y, XIE X. Discovering Regions of Different Functions in a City Using Human Mobility and POIs[C]//ACM Sigkdd International Conference on Knowledge Discovery and Data Mining. [S. l. ]: ACM, 2012. http://dl.acm.org/citation.cfm?id=2339561 |
| [10] | MOUSAVI S M, HARWOOD A, KARUNASEKERA S, et al. Geometry of Interest (GOI):Spatio-temporal Destination Extraction and Partitioning in GPS Trajectory Data[J]. Journal of Ambient Intelligence and Humanized Computing, 2016: 1–16. |
| [11] | PANG L X, CHAWLA S, LIU W, et al. On Detection of Emerging Anomalous Traffic Patterns Using GPS Data[J]. Data & Knowledge Engineering, 2013, 87(9): 357–373. |
| [12] | 龙瀛, 张宇, 崔承印. 利用公交刷卡数据分析北京职住关系和通勤出行[J]. 地理学报, 2012, 67(10): 1339–1352. DOI:10.11821/xb201210005 |
| [13] | 徐金垒, 方志祥, 萧世伦, 等. 城市海量手机用户停留时空分异分析——以深圳市为例[J]. 地球信息科学学报, 2015, 17(2): 197–205. |
| [14] | 陈佳, 胡波, 左小清, 等. 利用手机定位数据的用户特征挖掘[J]. 武汉大学学报(信息科学版), 2014, 39(6): 734–738. |
| [15] | 常晓猛, 乐阳, 李清泉, 等. 利用位置的虚拟社交网络地理骨干网提取[J]. 武汉大学学报(信息科学版), 2014, 39(6): 706–710. |
| [16] | 李婷, 裴韬, 袁烨城, 等. 人类活动轨迹的分类、模式和应用研究综述[J]. 地理科学进展, 2014, 33(7): 938–948. DOI:10.11820/dlkxjz.2014.07.009 |
| [17] | KOBAYASHI T, SHINAGAWA N, WATANABE Y. Vehicle Mobility Characterization Based on Measurements and Its Application to Cellular Communication Systems (Special Issue on Multimedia Mobile Communication Systems)[J]. Ieice Transactions on Communications, 1999, 82(12): 2055–2060. |
| [18] | 许宁, 尹凌, 胡金星. 从大规模短期规则采样的手机定位数据中识别居民职住地[J]. 武汉大学学报(信息科学版), 2014, 39(6): 750–756. |
| [19] | WON J I, KIM S W, BAEK J H, et al. Trajectory Clustering in Road Network Environment[J]. IEEE Symposium on Computational Intelligence and Data Mining, 2009(3): 299–305. |
| [20] | 吴笛, 杜云艳, 易嘉伟, 等. 基于密度的轨迹时空聚类分析[J]. 地球信息科学学报, 2015, 17(10): 1162–1171. |
| [21] | 宋乐怡. 海量出租车轨迹数据分析与位置推荐服务[D]. 上海: 华东师范大学, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10269-1015339246.htm |
| [22] | HAN J, KAMBER M. Data Mining:Concepts and Technique[M]. [S.l.]: Morgan Kaufmann Publishers Inc., 2006. |
| [23] | 孙吉贵, 刘杰, 赵连宇. 聚类算法研究[J]. 软件学报, 2008, 19(1): 48–61. |
| [24] | MACQUEEN J. Some Methods for Classification and Analysis of Multivariate Observations[C]//Proceedings of Berkeley Symposium on Mathematical Statistics and Probability. [S. l. ]: University of California Press, 1967. |
| [25] | KAUFMAN L, ROUSSEEUW P J. Finding Groups in Data:An Introduction to Cluster Analysis[M]. [S.l.]: John Wiley & Sons, Inc., 2008. |
| [26] | DEMPSTER A, LAIRD N, RUBIN D. Maximum Likelihood Eitimation from Imcomplete Data via EM Algorithm[J]. Journal of the Royal Statistical Society:Series B, 1977, 39: 1–38. |
| [27] | MOHAMED O O K, EL-SHARKAWI M E, MOKHTAR H, et al. Mining Moving Objects Trajectories[J]. 2012. https://www.researchgate.net/publication/256457462_Mining_Moving_Objects_Trajectories |
| [28] | PARK H S, JUN C H. A Simple and Fast Algorithm for K-medoids Clustering[J]. Expert Systems with Applications, 2009, 36(2): 3336–3341. DOI:10.1016/j.eswa.2008.01.039 |
| [29] | 何彬彬, 方涛, 郭达志. 基于不确定性的空间聚类[J]. 计算机科学, 2004, 31(11): 196–198. DOI:10.3969/j.issn.1002-137X.2004.11.053 |
| [30] | ZHONG C, MIAO D, FRÄNTI P. Minimum Spanning Tree Based Split-and-merge:A Hierarchical Clustering Method[J]. Information Sciences, 2011, 181(16): 3397–3410. DOI:10.1016/j.ins.2011.04.013 |
| [31] | ZHANG T, RAMAKRISHNAN R, LINVY M. BIRCH:An Efficient Data Clustering Method for Very Large Databases[J]. ACM Sigmod International Conference on Management of Data, 1996, 25(2): 103–114. DOI:10.1145/235968 |
| [32] | ROUSSEEUW P J, KAUFMAN L. Finding Groups in Data[J]. Series in Probability & Mathematical Statistics, 1990, 34(1): 111–112. |
| [33] | GUHA S, RASTOGI R, SHIM K. ROCK:A Robust Clustering Algorithm for Categorical Attributes[J]. Information Systems, 1999, 25(5): 345–366. |
| [34] | TU Y, LIU Y, LI Z. Online Segmentation Algorithm for Time Series Based on BIRCH Clustering Features[C]//International Conference on Computational Intelligence and Security. Nanning: SCIS, 2010. http://doi.ieeecomputersociety.org/10.1109/CIS.2010.19 |
| [35] | SHAO X, CHENG W. Improved CURE Algorithm and Application of Clustering for Large-scale Data[C]//International Symposium on IT in Medicine and Education (ITME). Guangzhou: IEEE, 2011. http://ieeexplore.ieee.org/document/6130839/ |
| [36] | HINNEBURG A, KEIM D A. An Efficient Approach to Clustering in Large Multimedia Databases with Noise[C]//Proceedings of the Fourth Data Mining. New York: AAAI Press, 1998. http://dl.acm.org/citation.cfm?id=3000302 |
| [37] | ESTER M, KRIEGEL H P, SANDER J, et al. A Density-based Algorithm for Discovering Clusters in Large Spatial Databases with Noise[C]//Proceeding of the Second International Conference on Knowledge Discovery and Data Mining. Portland: AAAI Press, 1996. http://www.researchgate.net/publication/221653977_A_Density-Based_Algorithm_for_Discovering_Clusters_in_Large_Spatial_Databases_with_Noise?ev=auth_pub |
| [38] | ANKERST M, BREUNIG M M, KRIEGEL H, et al. OPTICS:Ordering Points to Identify the Clustering Structure[J]. ACM SIGMOD Record, 1999, 28(2): 49–60. DOI:10.1145/304181 |
| [39] | SCHOIER G. On the MDBSCAN Algorithm in a Spatial Data Mining Context[J]. Data Mining Concepts Methodologies Tools & Applications, 2013, 7974: 375–388. |
| [40] | EDLA D R, JANA P K. A Grid Clustering Algorithm Using Cluster Boundaries[J]. Information and Communication Technologies, 2013, 15(3): 254–259. |
| [41] | 周涛, 陆惠玲. 数据挖掘中聚类算法研究进展[J]. 计算机工程与应用, 2012, 48(12): 100–111. DOI:10.3778/j.issn.1002-8331.2012.12.021 |
| [42] | 赵慧, 刘希玉, 崔海青. 网格聚类算法[J]. 计算机技术与发展, 2010, 20(9): 83–85. |
| [43] | WANG W, YANG J, MUNTZ R R. STING: A Statistical Information Grid Approach to Spatial Data Mining[C]//Proceedings of International Conference on Very Large Data Bases. Athens, Greece: Morgan Kaufmann Publishers Inc., 1997. http://dl.acm.org/citation.cfm?id=758369 |
| [44] | AGRAWAL R, GEHRKE J, GUNOPULOS D, et al. Automatic Subspace Clustering of High Dimensional Data for Data Mining Applications[J]. ACM, 1998, 27(2): 94–105. |
| [45] | 邓敏, 刘启亮, 李光强, 等. 基于场论的空间聚类算法[J]. 遥感学报, 2010, 14(4): 694–709. |
| [46] | IZAKIAN Z, MESGARI M S, ABRAHAM A. Automated Clustering of Trajectory Data Using a Particle Swarm Optimization[J]. Computers, Environment and Urban Systems, 2016, 55: 55–65. DOI:10.1016/j.compenvurbsys.2015.10.009 |
| [47] | LI Y, HAN J, YANG J. Clustering Moving Objects[C]//Proceedings of the Tenth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Seattle: ACM, 2004. http://dl.acm.org/citation.cfm?id=1014129 |
| [48] | 贺玲, 吴玲达, 蔡益朝. 数据挖掘中的聚类算法综述[J]. 计算机应用研究, 2007, 24(1): 10–13. |
| [49] | TUNG A K H, HOU J, HAN J, et al. Spatial Clustering in the Presence of Obstacles[C]//2013 IEEE 29th International Conference on Data Engineering. Herdelberg: ICDE, 2001: 359-367. http://dl.acm.org/citation.cfm?id=879654 |
| [50] | LIU W, FENG J, WANG Z. Constrained Clustering Objects on a Spatial Network[C]//2009 WRI World Congress on Computer Science and Information Engineering. Los Angeles: IEEE, 2009. http://doi.ieeecomputersociety.org/10.1109/CSIE.2009.12 |
| [51] | 廖律超, 蒋新华, 邹复民, 等. 浮动车轨迹数据聚类的有向密度方法[J]. 地球信息科学学报, 2015, 17(10): 1152–1161. |
| [52] | 王金凤, 邢长征. 基于道路网络的移动对象聚类[J]. 计算机工程与应用, 2016, 52(7): 74–78. |
| [53] | 马林兵, 李鹏. 基于子空间聚类算法的时空轨迹聚类[J]. 地理与地理信息科学, 2014, 30(4): 7–11. |
| [54] | LEE J G, HAN J, WHANG K Y. Trajectory Clustering: A Partition-and-group Framework[C]//ACM SIGMOD International Conference on Management of Data. Beijing: ACM, 2007. http://dl.acm.org/citation.cfm?id=1247546 |
| [55] | HAN B, LIU L, OMIECINSKI E. NEAT: Road Network Aware Trajectory Clustering[C]//IEEE International Conference on Distributed Computing Systems. [S. l. ]: IEEE, 2012. http://ieeexplore.ieee.org/document/6257987/ |


