编组站是铁路枢纽的核心,是车流集散和列车解编的基地,其内部线路设计横纵交错、复杂度极高,给大尺度地图表达的编组站数据缩编至小比例尺带来了较大难度。
选取是地图缩编的基础。编组站隶属交通道路要素,早期的选取通常只考虑道路的等级和属性,有时按照条件-结论规则进行选取[1];Kreveld等提出在依据等级取舍的基础上,通过判断道路节点以外点的距离是否小于限差,决定取舍[2]。一般编组站实际地图数据未赋属性值,显然依据以上方法难以奏效。此外,根据道路网眼节点强度值和密度[3]、层次骨架控制[4]等进行选取均是交通道路选取的常用方法。但编组站内部线路组成网眼的节点数量相比道路网眼少,层次结构不突出,实践证明应用上述方法的取舍效果不理想。
全国范围内编组站数量不足百个,导致研究者对此缺乏重视,鲜见国内外文献资料探讨其综合选取的方法,而大量有关交通道路[5]和河流水系的研究成果[6-7]又不适用于此。当开展自动化地图综合时,编组站这类要素无法回避,因此,本文系统分析编组站空间布局和拓扑特性,精练出6种地图特征,提出铁路编组站综合选取的3大基本原则,并据此设计自动化处理方法,通过实际数据测试,验证这些基本原则的合理性和方法的有效性。
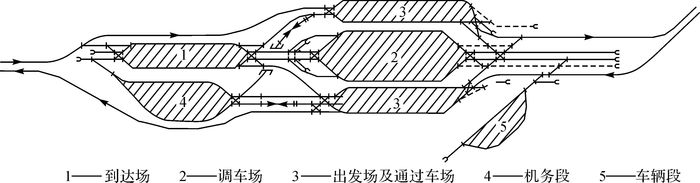
1 编组站的结构特征、拓扑特征和地图特征 1.1 结构特征编组站的结构组成主要包含各种“场”、车辆段、机务段、牵出线、驼峰及相关附属设施等部分。根据不同场排列形式的不同,编组站可分为3种基本结构:纵列式、横列式和混合式,如图 1所示。
|
| 图 1 混合式编组站 |
虽然编组站的类型不尽相同,但线路设计遵循一定规律。一般来说,各种“场”内线路比较密集,网眼强度大,用于办理列车的解体和编组作业;驼峰为连接各“场”中间的线路,结构简单,连通性较强;牵出线整体观察具有平行特征,线路延展性较好,主要办理列车的到达和出发作业;附属设施多为零散、短小线路,用于放置长期废弃或作为零部件的车皮等设备。
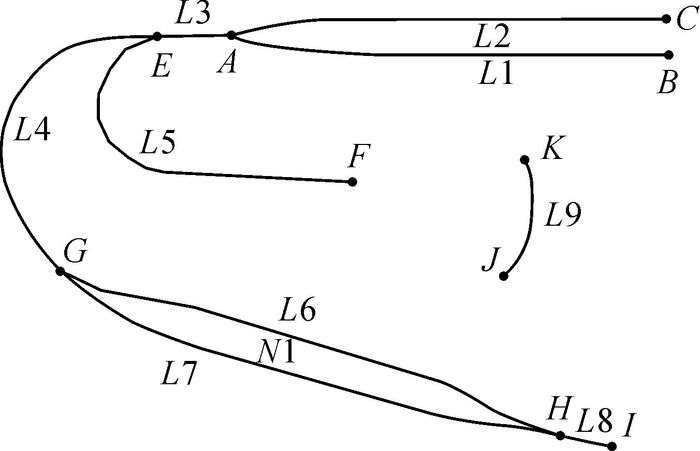
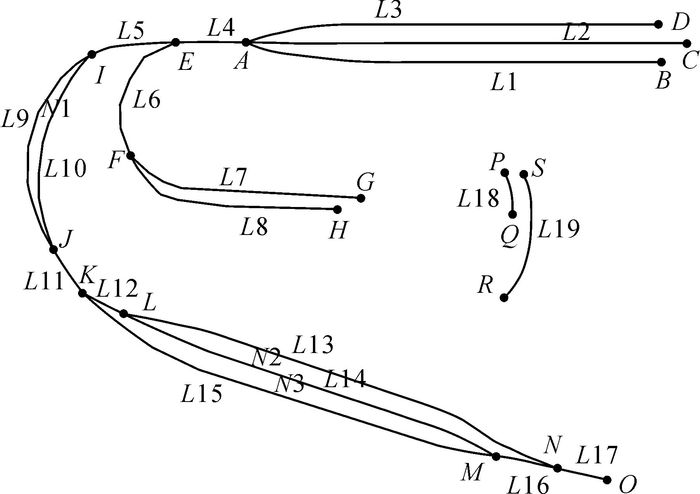
1.2 拓扑特征空间布局及其结构特征确定了编组站内部的拓扑特性。根据内部线路节点与弧段的拓扑关系[8],将其分解为3种弧段模型[9]:孤立弧、悬挂弧和中间弧。孤立弧首尾结点不同,且都仅关联弧段本身(如图 2中L18、L19);悬挂弧首尾结点中有且只有一个结点仅关联弧段本身(如图 2中L1、L2、L3、L7、L8、L17);中间弧首尾结点均有除本身外的其他关联弧段(如图 2中的L4-L6、L9-L16)。
|
| 图 2 空间特征示意 |
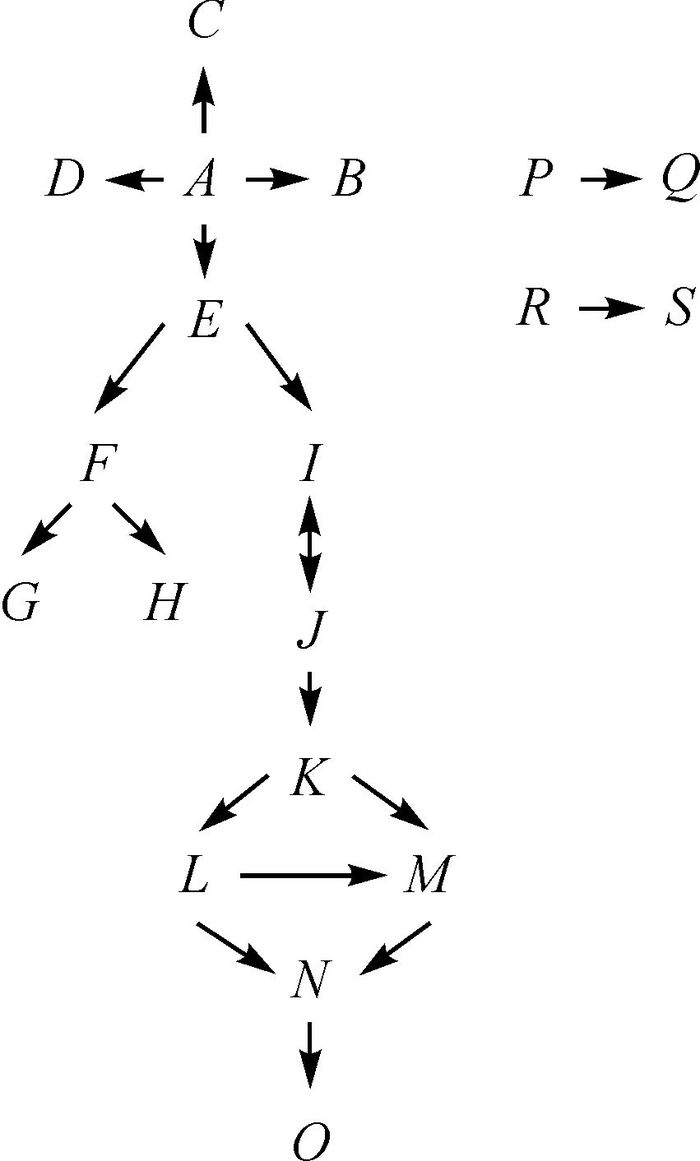
在透彻分析结构和拓扑特征基础上,精练出6种地图特征:断头弧、同节点弧、相似弧、网眼弧、平行弧和主干弧。依据图 2的拓扑特征,建立结点拓扑关系树(如图 3所示)和拓扑信息结构表(见表 1),清晰地表达结点、弧段之间的拓扑关联性及拓扑连通性。
|
| 图 3 结点拓扑关联树 |
| (a)结点结构表 | |||||
| (Node:结点;ArcNumber:结点关联弧段数;ArcList:弧段列表) | |||||
| Node | ArcNumber | ArcList | |||
| A | 4 | L1、L2、L3、L4 | |||
| B | 1 | L1 | |||
| C | 1 | L2 | |||
| D | 1 | L3 | |||
| E | 3 | L4、L5、L6 | |||
| F | 3 | L6、L7、L8 | |||
| G | 1 | L7 | |||
| H | 1 | L8 | |||
| I | 3 | L5、L9、L10 | |||
| J | 3 | L9、L0、L11 | |||
| K | 3 | L11、L12、L15 | |||
| L | 3 | L12、L13、L14 | |||
| M | 3 | L14、L15、L16 | |||
| N | 3 | L13、L16、L17 | |||
| O | 1 | L17 | |||
| P | 1 | L18 | |||
| Q | 1 | L18 | |||
| R | 1 | L19 | |||
| S | 1 | L19 | |||
| (b)弧段结构表 | |||||
| (Arc:弧段;SNode:首节点;ENode:尾节点;LPolygon:左多边形;RPolygon:右多边形;Length:实际长度;-表示空) | |||||
| Arc | SNode | ENode | LPolygon | RPolygon | Length |
| L1 | A | B | - | - | 148 |
| L2 | A | C | - | - | 157 |
| L3 | A | D | - | - | 149 |
| L4 | A | E | - | - | 25 |
| L5 | E | I | - | - | 30 |
| L6 | E | F | - | - | 46 |
| L7 | F | G | - | - | 85 |
| L8 | F | H | - | - | 79 |
| L9 | I | J | - | N1 | 73 |
| L10 | I | J | N1 | - | 68 |
| L11 | J | K | - | - | 17 |
| L12 | K | L | - | N3 | 15 |
| L13 | L | N | - | N2 | 163 |
| L14 | L | M | N2 | N3 | 141 |
| L15 | K | M | N3 | - | 158 |
| L16 | M | N | N2 | - | 22 |
| L17 | N | O | - | - | 18 |
| L18 | P | Q | - | - | 13 |
| L19 | R | S | - | - | 42 |
| (c)网络多边形结构表 | |||||
| (NetPolygon:网眼多边形;ArcNumber:弧段数;ArcList:弧段列表) | |||||
| NetPolygon | ArcNumber | ArcList | |||
| N1 | 2 | L9、L10 | |||
| N2 | 3 | L13、L14、L16 | |||
| N3 | 3 | L12、L14、L15 | |||
(1) 断头弧,即拓扑特征中的孤立弧,主要由编组站中的附属设施组成。该类弧的首尾结点连通性为“1”,无左右多边形,如图 2中L18、L19。
(2) 同节点弧,编组站中首尾点均相同的两条中间弧,夹角较小,主要用于两辆车之间的货物转送。该类弧首尾结点的连通性为“3”,左右多边形其中一侧为空,如图 2中L9、L10。
(3) 相似弧,两条悬挂弧,由同一结点连接,两者间的夹角与间距很小,主要用于多辆车之间的货物转送。该类弧首尾结点其中一个连通性为“3”,另一个连通性为“1”,左右多边形均为空,如图 2中L7、L8。
(4) 网眼弧,编组站中组成闭合多边形的中间弧段,各种“场”中的弧段一般为网眼弧段,如图 2中多边形N1、N2、N3的组成弧段。
(5) 平行弧,编组站的牵出线和配套设施中,很多线路都近似平行,并且相邻弧段之间的差距相差不大,一般由多条悬挂弧段组成。首尾结点其中一个连通性为“3”,另一个连通性为“1”,左右多边形均为空,如图 2中L1~L3组成的结构。
(6) 主干线,即驼峰中的弧段,一般由非网眼弧的中间弧构成。该类弧首尾结点连通性不小于“2”,左右多边形均为空,如图 2中L5、L11。
2 选取基本原则及自动处理方法综合选取的长度和间距阈值取决于原始尺度和目标尺度,当几条弧段同时满足取舍条件时,取决于对结构健壮性和拓扑延展性的贡献和价值。因此,综合选取应满足视觉可辨析、结构健壮性和拓扑延展性等一些基本原则与要求。
2.1 视觉可辨析原则通过对大量编组站数据的研究分析发现,发车线、调车线、到达线的有效长度大约为600~1000 m,其余线路(除主干线外)长度多小于600 m,因此,编组站的综合通常涉及1:500~1:25 000,1:25 000以下图中只保留编组线主体形状,内部线路已无需表示。参考国内外地图表达规范,在1:25 000尺度的地图中,隧道、台阶、地类界等线状类长度的约束图上长度不小于1 mm,站线间距不应小于0.3 mm,否则人眼视觉难以辨识,从信息度量的角度,即使保留此类要素,复杂度剧增且信息量冗余[10]。以此为基础,推演1:Scale (Scale>25 000) 的长度阈值(式(1)、式(2))和间距阈值确定模型(式(3)、式(4))[11]。
(1) 长度阈值
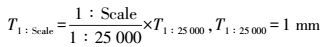 (1)
(1) 式中,T1:25 000为1:25 000尺度图上最小可辨长度,一般取值为1 mm;1:Scale为某地图尺度;T1:Scale为1:Scale尺度图上最小可辨长度。
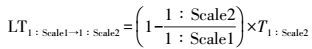 (2)
(2) 式中,LT1:Scale1→1:Scale2为1:Scale1尺度图上长度取舍阈值;1:Scale1为原始比例尺;1:Scale2为目标比例尺;T1:Scale2为1:Scale2尺度图上最小可辨长度,由式(1) 计算可得。
(2) 间距阈值
 (3)
(3) 式中,SpaceT1:25 000为1:25 000尺度图上最小可辨间距,一般取值0.3 mm;1:Scale为某地图尺度;SpaceT1:Scale为1:Scale尺度图上最小可辨间距。
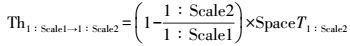 (4)
(4) 式中,Th1:Scale1→1:Scale2为1:Scale1尺度图上间距取舍阈值;1:Scale1为原始比例尺;1:Scale2为目标比例尺;SpaceT1:Scale2为1:Scale2尺度图上最小可辨间距,由式(3) 计算可得。
(3) 计算实例
图 2数据原始比例尺为1:500,目标比例尺为1:10 000,由式(1) 计算出图上1:10 000最小可辨长度T1:10 000=2.5 mm,由式(2) 计算出长度阈值LT1:500→1:10 000=2.375 mm;由式(3) 计算出图上宽度阈值SpaceT1:10 000=0.75 mm,由式(4) 计算出间距阈值Th1:500→1:10 000=0.712 5 mm。
2.2 结构健壮性原则人工综合时,经过直观定性分析,保留主要的骨架线路,删除次要的线路;计算机自动化处理时,主要依赖阈值和可定量化的结构特征与拓扑特征,最大可能性保持原结构至关重要。
2.2.1 断头弧处理根据长度阈值LengthEplison,将所有几何长度小于LengthEplison的断头弧放入容器中,然后从拓扑结构中删除,并更新拓扑关系。如图 2中L18的几何长度D18=13 m/10 000=1.3 mm < LengthEplison=2.375 mm,因此,L18被删除,从而达到删除零碎道路、保持整体结构的效果。
2.2.2 平行弧处理找到悬挂弧,选取能表达弧段特征的采样点组成新的弧段arc;根据间隔阈值SpaceEplison为缓冲半径建立arc的矩形缓冲区,拓扑查询与缓冲区相交的所有弧段,得到缓冲区内位于arc两侧最近的两条弧段arc1和arc2,计算arc1、arc2的间距,若小于SpaceEplison,则删除当前弧段,更新拓扑关系。其中,arc1和arc2的间隔Spacearc1→arc2由式(5) 进行计算
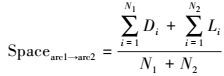 (5)
(5) 式中,N1、N2为分别在两条弧上取得的采样点的数量;Di和Li分别为一条弧上的采样点到另一条弧上的距离。
图 2中的L2根据间距阈值SpaceEplison建立缓冲区后,得到缓冲区内的弧段L1和L3,计算间距值S=14 m/10 000=1.4 mm>SpaceEplison=0.712 5 mm,L1和L2、L2和L3之间的间距值S=7 m/10 000=0.7 mm < SpaceEplison=0.712 5 mm,因此删除L2,保留L1、L3,主体结构保持不变。
2.2.3 同节点弧和相似弧处理这两类地图特征都具有弧段之间的夹角很小、形状相似的特点,因此在综合时只需保留一条弧段用于表达地物特征即可。若由式(5) 计算的间距小于间距阈值,则保留长度较大的弧段,删除长度较小的弧段。
图 2中的同节点弧L9和L10,相似弧段L7和L8,间隔均在阈值范围内,根据几何长度,删除L8、L10,保留L7、L9。
2.3 拓扑延展性原则综合选取要保证线路整体的拓扑延展性,尽管有些弧段长度较小,但对于维持站内整体连通性具有重要作用,需要保留。根据这一原则,完成主线和网眼弧的自动化处理。
2.3.1 主线处理根据首尾结点连通性不小于“2”,且左多边形均为空的拓扑特性,确定主线。由于主线具有连接各“场”、保持拓扑连通性等关键作用,应予以保留。
2.3.2 网眼弧处理删除相邻网眼的共享弧并不影响网眼中其余结点间的连通性,因此对于网眼弧的处理主要是删除共享弧。对于单个网眼,若组成弧段个数等于2,则按照同节点弧的处理方式进行处理;否则,将按照结点连通性处理。
根据图 4(a),构建网眼弧段结点拓扑关联树(如图 4(b)所示),从首结点J开始,依次判断删除当前结点关联弧段后是否影响网眼拓扑连通性,若不影响,则从拓扑结构中删除此条弧段及其关联的左右多边形,直至末结点O结束。如图 4(a)中,发现删除L、M两个结点所关联的弧段L14后并不影响连通性,因此删除L14,并将左多边形N2和右多边形N3从拓扑中删除。
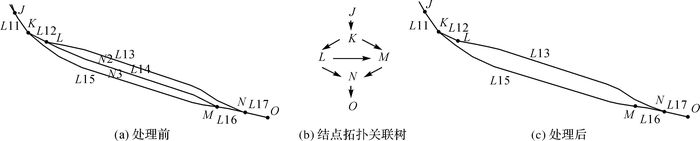
|
| 图 4 网眼弧处理 |
该流程分为3个主要步骤:① 根据原始比例尺和目标比例尺确定长度和间距阈值;② 构建拓扑关系,对基础数据进行拓扑预处理,包括弧段自相交处理、结点拟合处理、去除重复线、去除假节点、删除冗余节点、删除短悬线、构建拓扑多边形等,针对预处理之后的数据,建立拓扑关联表,以实现对断头弧、同节点弧、相似弧、网眼弧等空间特征的识别;③ 对编组站的6个地图特征进行分类处理,先处理断头弧,再处理网眼弧段和平行弧段,最后处理上述两步剩余的同节点弧和相似弧。图 5为图 2从1:500到1:10 000自动化综合的取舍结果。
3 试验与分析本文以成都东站混合式编组为研究案例,区域范围约为30 km2,原始比例尺为1:500(如图 6(a)所示),共有609条弧段。这一编组站数据具有出发场、调车场、到达场等要素,6类地图特征均蕴含其中。试验依托中国测绘科学研究院研制的WJ-Ⅲ地图工作站,首先利用文献[5]中的道路网选取方法,将地形图综合至1:10 000;然后将本文提出的编组站综合取舍方法嵌入到工作站中,根据上文中提到的阈值确定模型,计算出长度阈值为2.375 mm,间隔阈值为0.712 5 mm,按照阈值对编组站中的线路进行选取。应用不同方法进行选取后的结果对比见表 2、图 6(b)、图 6(c)。
| 数据 | 处理方法 | 弧段个数 | 选取比例 | 总长度/m | 处理时间/s |
| 1:500原始数据 | - | 609 | - | 109 839.7 | - |
| 1:10 000选取后数据 | 道路网选取方法 | 358 | 50.0% | 71 201.0 | 0.61 |
| 本文方法 | 99 | 16.3% | 54 268.4 | 0.25 |
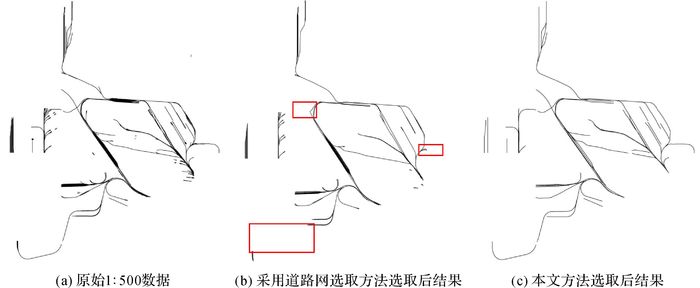
|
| 图 6 综合选取前后结果对比 |
综合分析上述统计结果,并对比前后地形图,不难看出:① 整个自动化处理时间为0.25 s,用时较短,效率较高;② 保留的弧段为99个,仅为原弧段的16.3%,选取效果明显;③ 编组站的主体结构得到了保留,对比图 6(b)中框选区域中重要线段丢失导致连通性破坏的情况,本文的选取方法保留了站间重要的连通性,并对密度较大的区间弧段进行了化简,删除了细碎、零星的弧段。
4 结语本文在分析编组站空间布局和拓扑特性的基础上,精练出6种地图特征,提出了铁路编组站综合选取的3大基本原则,推导了长度和间距阈值的计算公式,并针对以上地图特征设计了自动化选取处理方法,依托中国测绘科学研究院研发的WJ-Ⅲ地图工作站,嵌入上述综合取舍算法。试验案例结果表明:保留弧段仅占原有弧段的16.3%,且编组站的主体结构完整,拓扑连通性好。
本文目前仅实现了编组站自动化综合取舍,对于弧段的简化和移位并未涉及,另外也没有与编组站属性数据结合,有待进一步探讨。
| [1] | 王光霞. 自动制图综合系统的研究及居民地道路自动综合的实现[D]. 郑州: 信息工程大学, 1994. |
| [2] | KREVELD M V, LUO J.The Definition and Computation of Trajectory and Subtrajectory Similarity[C]//Proceedings of the 15th Annual ACM International Symposium on Advances in Geographic Information Systems.[S.l.]:ACM, 2007:44. |
| [3] | 胡云岗, 陈军, 李志林, 等. 基于网眼密度的道路选取方法[J]. 测绘学报, 2007, 36(3): 351–357. |
| [4] | 何海威, 钱海忠, 刘海龙, 等. 道路网层次骨架控制的道路选取方法[J]. 测绘学报, 2015, 44(4): 453–461. DOI:10.11947/j.AGCS.2015.20130787 |
| [5] | 杨敏, 艾廷华, 周启. 顾及道路目标stroke特征保持的路网自动综合方法[J]. 测绘学报, 2013, 42(4): 581–587. |
| [6] | 翟仁建, 武芳, 邓红艳, 等. 基于遗传多目标优化的人工河网自动选取模型[J]. 测绘学报, 2008, 37(1): 108–331. |
| [7] | 艾廷华, 刘耀林, 黄亚锋. 河网汇水区域的层次化剖分与地图综合[J]. 测绘学报, 2007, 36(2): 231–236. |
| [8] | 王鹏波, 武芳, 翟仁健. 一种用于道路网综合的拓扑处理方法[J]. 测绘科学技术学报, 2009, 26(1): 64–68. |
| [9] | 李飞, 栾学晨, 杨必胜, 等. 高等级道路网的拓扑自动保持方法[J]. 武汉大学学报(信息科学版), 2014, 39(6): 729–733. |
| [10] | YANG Bisheng, LUAN Xuechen, LI Qiuping. Generating Hierarchical Strokes from Urban Street Networks Based on Spatial Pattern Recognition[J]. International Joural of Geographical Information Science, 2011, 25(12): 2025–2050. DOI:10.1080/13658816.2011.570270 |
| [11] | YU Z.The Effects of Scale Change on Map Structure[D].Worcester:Clark University, 1993:27-61. |