2. 河南理工大学矿山空间信息技术国家测绘地理信息局重点实验室, 河南 焦作 454003
2. Key Laboratory of Mine Spatial Information Technologies, NASG, Henan Polytechnic University, Jiaozuo 454003, China
GIS查询是从众多的时空实体中选择满足用户要求的空间实体[1],空间分析是GIS的核心内容之一[2]。矢量数字地图中道路信息主要以折线(由一系列的道路节点组成)形式表示,而道路缓冲区则主要是以折线对象为中心线形成的多边形区域[3]。判断点与多边形关系的叠加分析是查询道路沿线地物信息的重要方法[4-5],常用的叠加分析多是基于多边形裁剪算法,文献[6]介绍了基于拓扑模型和简单数据模型的两类算法,在比较两者优劣性基础上提出基于交点搜索的多边形叠加分析算法。现有的多边形裁剪算法多针对具体类型的多边形,使得算法复杂、时间消耗大,如Sutherl-Hodgeman、梁-Barsky、NLN算法要求裁剪多边形是凸多边形[7-9]。Weiler算法,以及近几年出现的Vatti算法及Greiner-Hormann算法[10-12],则可以处理一般常见的多边形。文献[12]提出用单线性链表数据结构的一般多边形裁剪算法,并与Vatti算法及Greiner-Hormann算法进行了对比分析。
上述算法需要遍历求出判断点与每一条折线段之间的最短距离,然后与缓冲区阈值进行比较,若小于阈值,则判定点在缓冲区内,否则不在缓冲区内。由此可见,这些算法计算过程烦琐、效率较低,不适用于节点较多且形状错综复杂的折线。针对上述问题,本文提出一种判断点是否在折线缓冲区内的矢量压缩算法,该方法通过对折线的逐步压缩和简化,确定与地物点相距最近的道路折线段,从而进行点与线的邻近度判断,实现空间查询功能。实例验证结果表明该算法快速、有效,具有一定的实际应用价值。
1 常用缓冲区分析方法 1.1 道路沿线缓冲区建立传统的缓冲区分析是在地理实体周围建立一定宽度的缓冲区多边形[13]。角分线法是建立折线缓冲区的最简单方法;凸角圆弧法则是为减小由于凸侧角点进一步变锐时,拐角凸侧处缓冲区远离折线节点所引起的偏差而用圆弧进行弥合,其中圆弧的两端点为过节点作其相邻两折线段的垂线并与凸侧缓冲区边界形成的交点[14-15]。本文采用凸角圆弧法建立折线缓冲区,并将点在道路折线缓冲区的情况分为3种:区域1表示端点处缓冲区、区域2表示拐角凸侧处缓冲区、区域3表示一般区域缓冲区,如图 1所示。
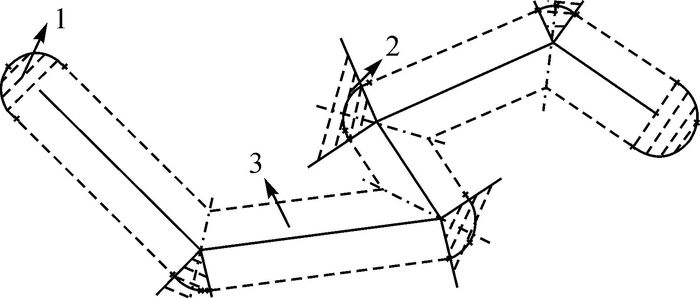
|
| 图 1 凸角圆弧法生成的折线缓冲区 |
端点缓冲区的判定步骤为(如图 2所示,以端点P0为例):
(1) 连接AP0、A1P0,在折线A、A1一侧分别与折线形成夹角∠AP0P1和∠A1P0P1。
(2) 若夹角≤90°,将此点直接过滤;反之,则将AP0与阈值d进行比较,此时如果AP0≤d,判断点A在端点P0的缓冲区内;若AP0>d,则不在该缓冲区内。
同理,对Pn进行分析,若点被过滤,则需进行后续算法。
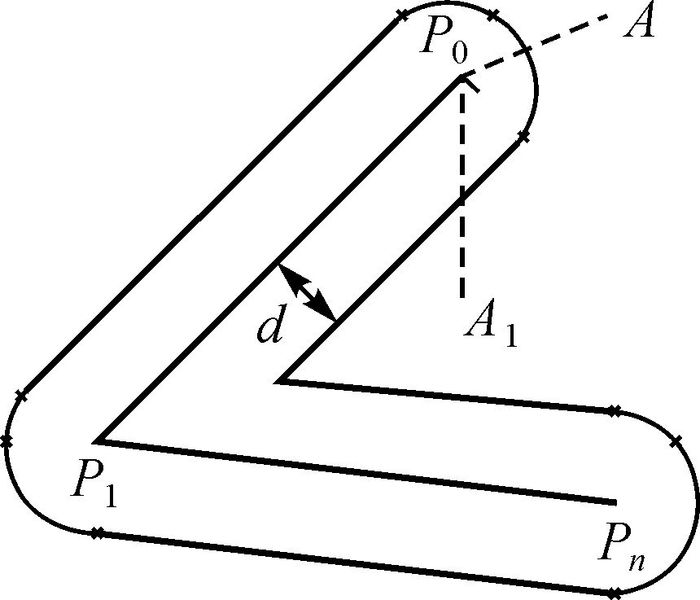
|
| 图 2 端点处缓冲区判断 |
用圆弧对折线在拐角凸侧区域进行拟合,形成凸角圆弧缓冲区。对经过由上节端点处过滤所剩余的点,可按下列步骤进行判定(如图 3所示):
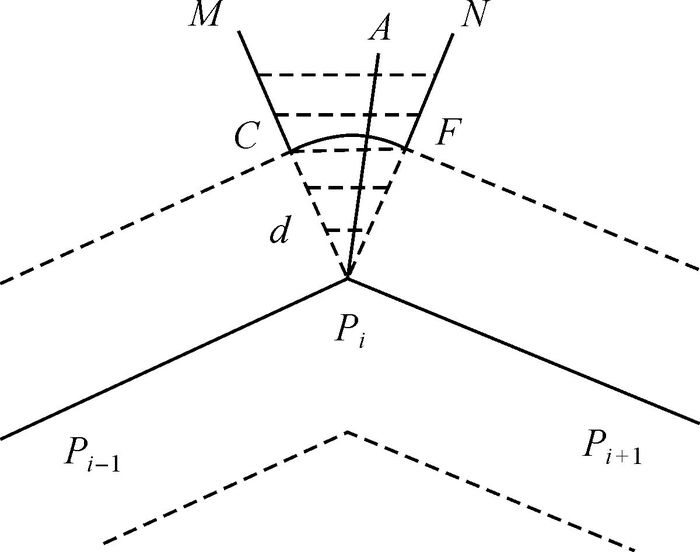
|
| 图 3 凸角圆弧缓冲区判断 |
(1) 连接APi并与折线在靠A点一侧形成夹角∠APiPi-1和∠APiPi+1。
(2) 若∠APiPi-1和∠APiPi+1均大于90°,则点在发散的扇形阴影区域PiMN内(若同时满足在多个节点凸侧的发散扇形阴影区域内,则将A与距离最近的节点Pi进行判断),予以保留,否则将该点过滤。
(3) 若APi≤d,则点A位于缓冲区内。
2 本文算法折线可以分为理想型折线和一般型折线两类。
理想型折线:折线每个拐弯处的夹角≥90°(如图 4所示),折线轨迹大幅度逐步远离起始点。
|
| 图 4 理想型折线 |
一般型折线:折线拐角处夹角有锐角有钝角,如“发夹弯”“十字路口自相交”等,使得折线呈各式各样且错综复杂(如图 5所示),在实际情况下此类折线更具有普遍性。
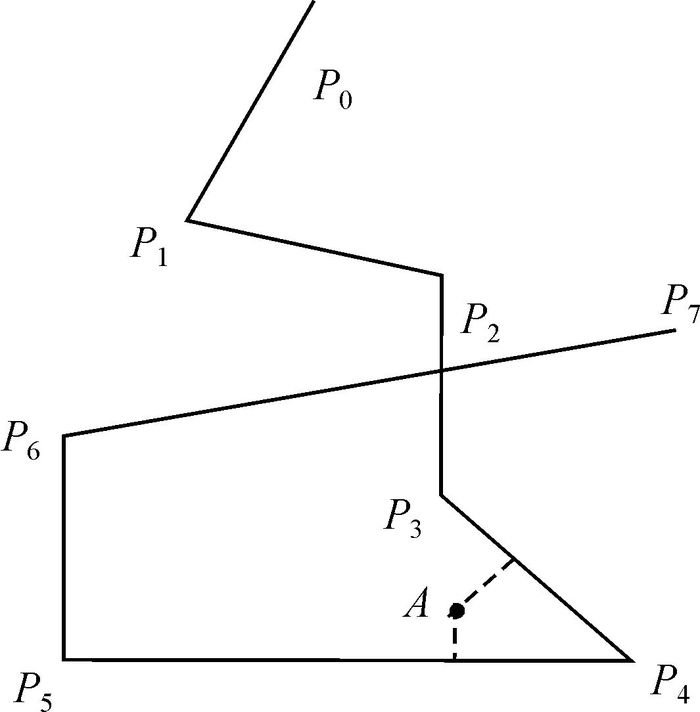
|
| 图 5 一般型折线 |
对于理想型折线可用较小夹角法对道路一般区域的点进行缓冲区分析,具体为:若使点A与某节点Pi的距离离最短,则设A仅可能与Pi相关的折线段形成缓冲区关系,通过比较APi与折线形成的临近A侧的两夹角大小,并过A对形成较小角的折线段作垂线,垂距L即为点到此折线的最短距离。
对于一般型折线,如图 5中点A与节点P3的距离最短,而实际上最短的折线是P4P5,与节点P3无关,因此较小夹角法无法适用一般型折线。
2.1 矢量压缩算法为适应一般型折线,本文提出基于矢量压缩的算法,即对被过滤的点采用基于矢量压缩算法进行判断。首先计算待判定点与某节点取得的最短距离,利用较小夹角法在局部进行初步缓冲区判断:
(1) 若判定点不在局部折线段的缓冲区内,可将其全部消去,并对折线进行压缩简化。
(2) 在折线断开处用虚拟线段连接,这样可以保证折线的连续性,并不参与后续计算。
(3) 判断点是否在缓冲区内,当点同时在多条折线段的阈值内,满足其中之一即可停止计算,或当折线无法再压缩时停止计算。
2.2 算法原理与实现 2.2.1 算法原理设P0、Pn分别为折线的起、始端点,Pi为中间节点(i=0, 1, 2,…,n),折线由节点及节点间的折线段组成,P_C、L_C表示组成折线的节点集合、线段集合,即
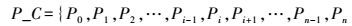 (1)
(1) 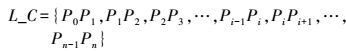 (2)
(2) S_C为遍历判定点与各节点间的距离集合
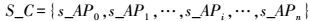 (3)
(3) 上述3个集合,可对折线本身及待判断点与折线关系进行描述:
(1) 点A为待判定的地物要素点,d为缓冲区阈值,L为计算得到的点与折线段的距离。
(2) 地图上各点的经纬度坐标已知,用(lat,lng)表示。
(3) 在压缩过程中,若出现两条虚拟线段相邻的情况,由于其均不参与计算,可自动将它们压缩合并,用新的虚拟线段取代。
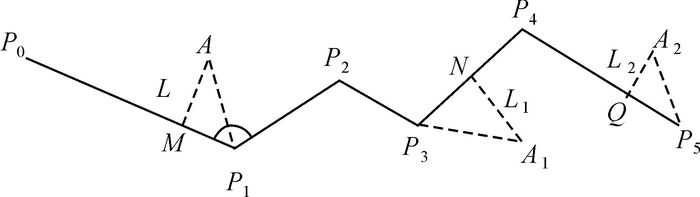
2.2.2 算法实现图 6为一般型折线,压缩算法的实现过程为:
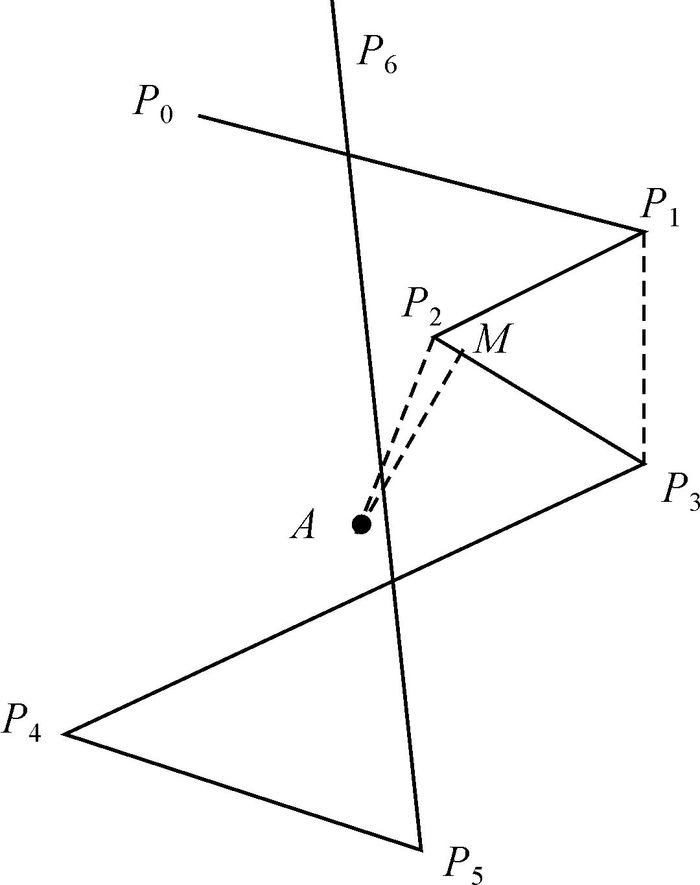
|
| 图 6 一般型折线 |
(1) 对点A到折线点集P_C中各节点遍历计算距离,得到距离集S_C。
(2) 从距离集S_C中取出A与某节点Pi间的最短距离Smin,令Smin=AP2。
(3) 连接APi,在折线靠A一侧形成两夹角∠APiPi-1和∠APiPi+1,通过比较可知:∠AP2P3=min(∠AP2P1,∠AP2P3)。根据较小夹角法,A点初步找到折线段P2P3,过A作垂直于P2P3的垂线AM,则A到线段P2P3的距离为
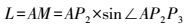 (4)
(4) (4) 若L≤阈值d,则点A在折线缓冲区内,计算结束;否则,去掉节点P2和线段P2P1、P2P3,形成虚拟线段P1P3,折线被第一次简化。折线每压缩一次,与折线相关的集合P_C、L_C、S_C均会发生改变,形成新的折线和新的点集合P_C、线段集合L_C及距离集合S_C。
(5) 对形成的新折线,重复步骤(1) -步骤(4),当判断出点A在折线缓冲区内,则立即停止计算;否则,继续简化压缩。
(6) 若折线再无法继续压缩(如图 7所示),且仍未判断出点在缓冲区内,则计算终止,说明点A不在折线缓冲区内。

|
| 图 7 判定点在折线缓冲区内的矢量压缩过程 |
为验证本文方法有效性,选择普通道路与复杂道路形状两种情况,对道路沿线地物信息进行查询试验。
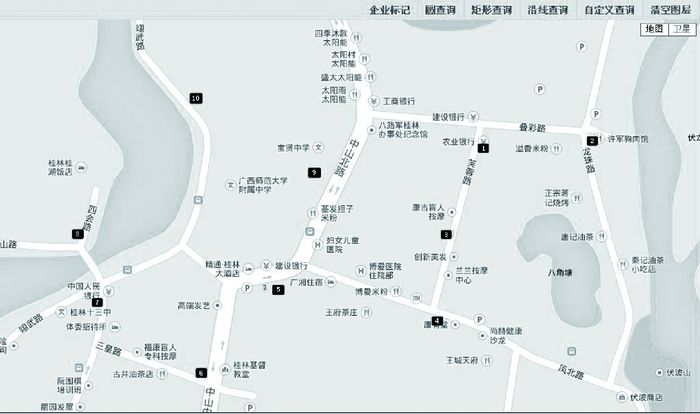
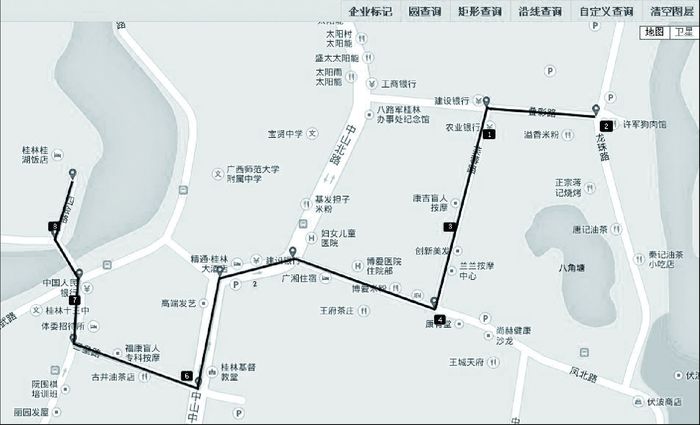
(1) 普通道路情况。在桂林市叠彩区标注米粉店若干(如图 8所示),然后沿“叠彩路-芙蓉路-凤北路-中山路-三皇路-四会路”轨迹在地图上画出道路沿线,设置缓冲区阈值为30 m。点击查询按钮,系统解析出此道路沿线周边的米粉店,并在图中显示(如图 9所示)。部分标记点的具体查询结果见表 1。
|
| 图 8 米粉店标记点位置 |
|
| 图 9 道路沿线缓冲区查询结果 |
| 地物点ID | 地物点坐标 | 与道路实际最短距离/m | 判断结果 | 准确与否 |
| 1 | (25.286 73, 110.301 18) | 14.788 | 是 | 是 |
| 2 | (25.286 84, 110.302 88) | 21.713 | 是 | 是 |
| 4 | (25.284 28, 110.300 46) | 21.250 | 是 | 是 |
| 5 | (25.284 72, 110.297 97) | 32.028 | 否 | 是 |
| 6 | (25.283 55, 110.296 77) | 13.243 | 是 | 是 |
| 9 | (25.286 38, 110.298 54) | 144.574 | 否 | 是 |
| 10 | (25.287 43, 110.296 68) | 228.421 | 否 | 是 |
(2) 复杂道路情况。与上述试验区相同,药店标记点位置如图 10所示,试验结果如图 11所示,试验具体数据见表 2。
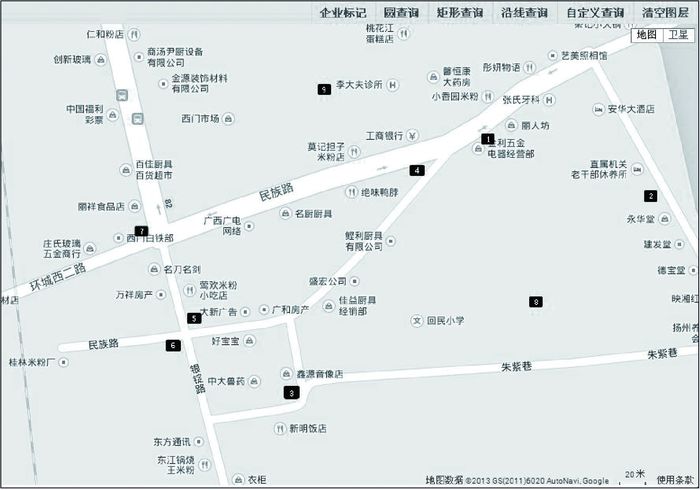
|
| 图 10 药店标记点位置 |
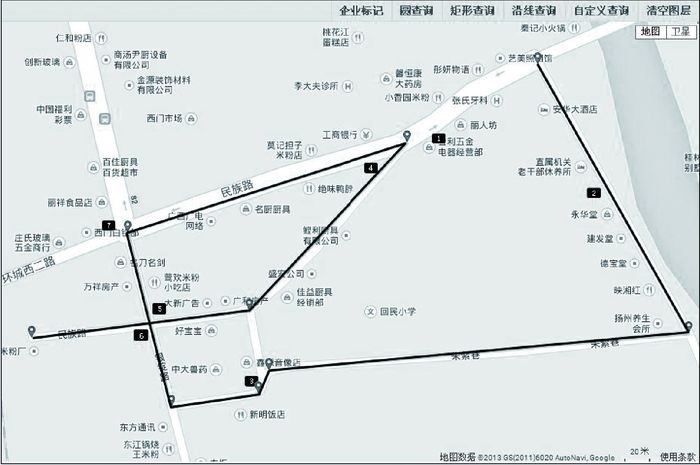
|
| 图 11 道路沿线缓冲区查询结果 |
| 地物点ID | 地物点坐标 | 与道路实际最短距离/m | 判断结果 | 准确与否 |
| 1 | (25.270 21, 110.284 20) | 22.098 | 是 | 是 |
| 2 | (25.269 85, 110.285 31) | 11.0 | 是 | 是 |
| 3 | (25.268 64, 110.282 85) | 10.036 | 是 | 是 |
| 4 | (25.270 02, 110.283 71) | 11.879 | 是 | 是 |
| 7 | (25.269 64, 110.281 83) | 15.962 | 是 | 是 |
| 8 | (25.269 21, 110.284 53) | 42.396 | 否 | 是 |
| 9 | (25.270 51, 110.283 08) | 60.942 | 否 | 是 |
通过上述试验,可得出如下结论:
(1) 本文算法查询准确率高,适用于各种类型的折线形式。
(2) 计算效率高,冗余小。当判断出地物信息在道路沿线缓冲区内,即停止计算。
(3) 仅利用道路节点和地物标记点的经纬度数据,通过夹角和欧氏距离即可进行计算。
4 结语本文提出了一种用于查询道路沿线地物信息的矢量压缩算法。试验结果表明,该算法对折线节点多、折线错综复杂等情况,具有较好的适应性,且在满足高精度的同时,降低了计算量,显著提高了计算效率。
| [1] | 沙薇, 盛业华, 杨林. 基于GIS的高速公路沿线设施管理信息查询系统的设计与实现[J]. 计算机应用与软件, 2009, 26(1): 112–114. |
| [2] | 王满, 孙海燕. 基于地图代数的缓冲区分析算法的研究[J]. 测绘信息与工程, 2009, 34(3): 33–34. |
| [3] | 赖云波, 孙棣华, 廖孝勇, 等. 基于道路缓冲区分析的地图匹配算法[J]. 计算机应用研究, 2011, 28(9): 3312–3314. |
| [4] | 王少华, 钟耳顺, 卢浩, 等. 基于非均匀多级网格索引的矢量地图叠加分析算法[J]. 地理与地理信息科学, 2013, 29(3): 17–20. |
| [5] | 朱效民, 赵红超, 刘焱, 等. 矢量地图叠加分析算法研究[J]. 中国图象图形学报, 2010, 15(11): 1696–1706. DOI:10.11834/jig.100182 |
| [6] | 薛胜, 潘懋, 王勇. 多边形叠置分析算法研究[J]. 计算机工程与应用, 2003(2): 57–59. |
| [7] | SUTHERLAND I E, HODGEMAN G W. Reentrant Polygon Clipping[J]. Communications of the ACM, 1974, 17(1): 32–42. DOI:10.1145/360767.360802 |
| [8] | LIANG Y, BARSKY B A. An Analysis and Algorithm for Polygon Clipping[J]. Communications of the ACM, 1983, 26(11): 868–877. DOI:10.1145/182.358439 |
| [9] | FOLEYJ D, DAM A, FEINER S K, et al. Computer Graphics, Principles and Practice[M]. Boston: Addison-Wesley, 1990. |
| [10] | 陈占龙, 吴信才, 吴亮, 等. 基于单调链和STR树的简单要素模型多边形叠置分析算法[J]. 测绘学报, 2010, 39(1): 102–108. |
| [11] | 陈占龙, 张丁文, 吴亮, 等. 基于图模型的多边形自动并行构建算法[J]. 计算机应用研究, 2012, 29(5): 1634–1636. |
| [12] | 刘勇奎, 高云, 黄有群, 等. 一个有效的多边形裁剪算法[J]. 软件学报, 2003, 14(4): 845–856. |
| [13] | 崔爽, 苏鸿, 叶良松, 等. 一种基于空间对象的缓冲区分析算法[J]. 地理与地理信息科学, 2011, 27(1): 38–41. |
| [14] | 王家耀. 空间信息系统原理[M]. 北京: 科学出版社, 2001: 291-309. |
| [15] | 邬伦, 刘瑜, 张晶, 等. 地理信息系统——原理、方法和应用[M]. 北京: 科学出版社, 2001: 168-171. |


