地球参考框架是地球参考系统的物理实现,它是由一系列基于特定的参考系统的点位坐标及其随时间的变化都精确已知的基准点组成。只有基于长期的、高精度的地球参考框架,才能确定地球上任意点位精确的绝对位置及其变化。目前, 理论背景最完善、精度最高、应用最广泛的全球参考框架是国际地球参考框架(internatiaonal terrestrial reference frame, ITRF),它为其他的全球和区域参考框架提供基准[1-2]。随着GPS、SLR、VLBI、DORIS等空间大地测量技术的不断改善和提高,它们在地球动力学方面得到广泛应用。虽然目前国际地球参考框架已经达到厘米级的精度,但依然无法满足全球性、大尺度范围内的地球动力学研究对其毫米级精度的需求。因此,国际地球参考框架的维持更新与精化,最终使精度达到毫米量级,是现代大地测量学的重要任务[3]。
近几十年来,在众多学者的努力下,利用各种空间大地测量技术的改进以及各基准站观测数据的持续积累,已使得高精度ITRF的建立成为可能。
1 ITRF发展概况ITRF是由国际地球自转与参考系统服务组织(International Earth Rotation and Reference Systems Service, IERS)通过全球分布的地面基准台站,基于GPS、SLR、VLBI、DORIS等空间大地测量技术的持续观测数据所建立的。IERS定义ITRF并给出实现这一理想定义的模型和方法,同时负责ITRF的维持更新与精化。
自1988年起,IERS已经发布了ITRF88、ITRF89、ITRF90、ITRF91、ITRF92、ITRF93、ITRF94、ITRF96、ITRF97、ITRF2000、ITRF2005和ITRF2008共12个版本的参考框架。其中,ITRF2005和ITRF2008是最具代表性的两个参考框架,也是ITRF日渐成熟的标志。二者的实现均采用坐标时间序列和地球定向参数作为输入数据,得到框架点的位置和线性速度以及与参考框架一致的地球定向参数, 目前ITRF2008的原点的长期稳定性已优于1 m,尺度精度优于1.2[4-5]。由于测站数量及时间跨度的增加,以及地震引起的震后变形等原因,IERS于2013年开始筹备新一代的ITRF,即ITRF2013。ITRF2013将补充2008-2013年5年间的观测数据,并于2014年8月发布。2014年底,IERS将新版本更名为ITRF2014,并要求各分析中心将提交的测站实测数据时间跨度扩充到2014年[14-15]。
2 ITRF最新进展 2.1 ITRF2014简介2016年1月21日,IERS发布了最新的参考框架版本ITRF2014, 这是继ITRF2008之后推出的新一代地球参考框架。ITRF2014仍采用GPS、SLR、VLBI、DORIS等空间大地测量技术观测地面基准站,随着其技术的不断改进,实测数据的持续更新和积累,处理策略的进一步完善,ITRF2014无论是在数据数量与质量、时序模型的建立以及全球测站分布的优化等方面上均有所提高。
ITRF2014的输入数据为IAG国际服务ILRS、IDS、IGS提供的卫星测量技术的周解,以及IVS提供的日解(站点坐标和地球定向参数EOP)。这4项技术观测时间跨度分别是32、21.8、21和35 a,且基于这4项技术的时间序列已分别由各自分析中心对该技术解进行了综合。
表 1为IAG服务所提交的技术解基本情况[6],从中可以看出,相较于ITRF2008、ITRF2014技术解所用时间序列跨度及基准台站数均有较大增加。同时,ITRF2014还将各个并置站之间的连接数据(由并置站、IGN测量部门、Z.Altamimi收集并提供)与大气载荷数据(由GGFC与基于NCEP的模型提供)作为输入数据[6]。此外,为了优化基准台站的全球分布和减少各种地震、设备更换等误差对站点的影响,ITRF2014对站点数量及其分布进行了适当的调整。图 1即为ITRF2014所用到的站点分布情况。
| 技术/分析中心 | 时间序列跨度 | 解/约束类型 | 所用台站数 |
| IGS | 1994-01-2015-02 | 最小约束处理 | 1576 |
| IDS | 1993-01-2014-09 | 最小约束处理 | 144 |
| ILRS | 1982-12-2015-01 | 松弛约束处理 | 116 |
| IVS | 1980-04-2014-12 | 无约束正则化处理 | 116 |
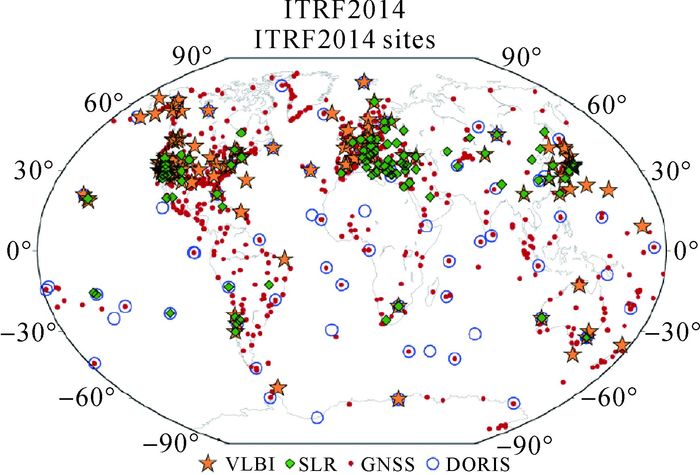
|
| 图 1 ITRF2014站点分布 |
为了确保ITRF2014与ITRF2008之间的联系,对于多数应用而言,有必要评估两框架之间的转换参数的一致性。ITRF2014与ITRF2008间的转换参数是由127个测站(其中包括89个GPS站、24个VIBL测站、8个SLR测站、2个DORIS测站)的实测数据计算而得。这些测站选择的主要标准为:① 有最佳的站点分布; ② 涉及尽可能多的VLBI、SLR、GPS和DORIS站; ③ 两框架之间的14个参数转换验后残差符合最好[5, 7]。ITRF2014与ITRF2008之间的转换参数与速率见表 2。
| T1/mm | T2/mm | T3/mm | D/10-9 | R1/mas | R2/mas | R3/mas | |
| 1.6 | 1.9 | 2.4 | -0.02 | 0.000 | 0.000 | 0.000 | |
| +/- | 0.2 | 0.1 | 0.1 | 0.02 | 0.006 | 0.006 | 0.006 |
| 0.0 | 0.0 | -0.1 | 0.03 | 0.000 | 0.000 | 0.000 | |
| +/- | 0.2 | 0.1 | 0.1 | 0.02 | 0.006 | 0.006 | 0.006 |
图 2为用于计算ITRF2014与ITRF2008之间转换参数的站点分布[8]。
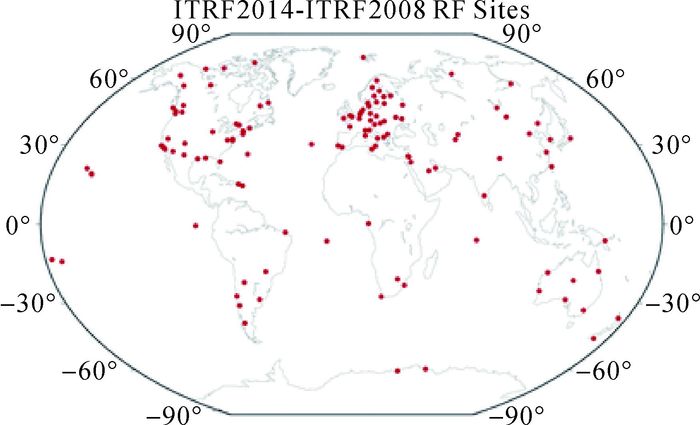
|
| 图 2 计算转换参数的站点 |
由于空间大地测量技术的改进、时间序列跨度的增加以及处理策略的变化,ITRF2014与ITRF2008将在各方面存在差异或改进。文献[7]有对ITRF2008的介绍,它们的主要区别如下[6, 8-10]:
2.3.1 框架参数定义除历元由ITRF2008的2005.0换成ITRF2014的2010.0之外,平移、旋转、尺度参数及其变化率均未改变。
2.3.2 数据分析策略ITRF2014在时间序列的叠加过程中,在足够的时间跨度下,给出了台站半年、一年期的预测信号,以及在建立时间序列的叠加正则方程组前,给出了震后形变模型进行修正,并应用到地震台站,而ITRF2008并未考虑地震对建模的影响。
2.3.3 模型的改进(1) 为提升地心运动观测精度,ITRF2008在原有激光动力学卫星观测的基础之上,增加了地球低轨卫星进行联合观测,但由于低轨卫星的模型误差以及GPS与DORIS对地心运动的解的抗差能力较弱,因此以ITRF2014在地心运动建模中,只基于SLR技术进行建模。
(2) 在对全球基准台站进行非线性运动建模时,不仅对季节性周期项进行估计,ITRF2014还首次考虑了非潮汐大气载荷,并对个体的大气载荷模型进行了改进。
(3) ITRF2014首次以测站振幅的时间函数的形式给出震后形变模型。测站位置坐标可以用XPSD表示,历元可用t表示,初始历元用t0表示,因此测站位置坐标可以表示为
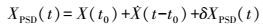 (1)
(1) 式中
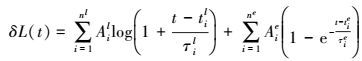 (2)
(2) 式中,nl表示模型中的对数项项数;ne表示模型中的指数项项数;Ail表示ith对数项的振幅;Aie表示ith指数项的振幅;τil表示ith对数项的阻尼时间;τie表示ith指数项的阻尼时间;til表示对应于ith对数项的地震时间;tie表示对应于ith的指数项时间。
3 毫米级ITRF的实现展望虽然最新推出的ITRF2014在参考框架定义、技术解处理策略、所用观测数据时间跨度的增加及数据质量、测站非线性运动建模等各方面均有所改进和提高,但距离毫米级精度ITRF的实现还有一定差距。在理想地球参考系统的理论基础上,毫米级国际地球参考框架的构建还需要解决测站非线性运动和地球质心运动的精确建模,以及多技术组合算法的完善这三大主要问题[12]。
3.1 测站非线性运动建模 3.1.1 季节性非线性变化建模大量研究表明,几乎所有的国际地球参考框架全球站点坐标时间序列都会有明显的周年、半周年,甚至更长时间的周期性运动和其他非线性运动趋势,以及跳跃与野值。通常认为引起测站季节性变化的影响因素包括地球物理效应(大气压、非潮汐海洋压力、大陆储水量的变化、冰后回弹等)及与空间大地测量技术(GPS、SLR、VLBI、DORIS等)有关的系统误差[12-15]。2002年2月,IERS所属的全球地球物理流体中心(Global Geophysical Fluids Center, GGFC)建立了负荷特殊管理局(Special Bureau Loading, SBL),其最终目的在于提供描述由大气压、非潮汐海洋压力、大陆储水量的变化等环境负载引起的形变信息的近实时全球数据集。文献[16-17]计算结果表明,仅80%IGS基准站的高程分量RMS经环境负载改正后减小,且环境负载造成的站点变动仅能解释高程分量的部分周年、半周年振幅,这已经是环境负载对GPS坐标时间序列影响的最好对比结果。除此之外,温度变化造成的热膨胀效应也对测站位移有影响。
为了提取时序中的季节性物理信号,应明确环境负载中各项负载及热膨胀效应对时间序列季节性趋势项的贡献,利用InSAR、GRACE等多源观测数据,引进现代信号处理方法提取形变信号,将经验季节性正弦函数模型与地球物理模型相结合, 以建立各项负载及热膨胀的精确模型[17]。ITRF2014已经首次考虑了非潮汐大气载荷,并对个体的大气载荷模型进行了改进,这为其他负载模型的建立提供了参考。
此外,已有文献表明, 与技术相关的系统误差(如未模型化的海洋极潮、残余对流层延迟等),数据处理策略的不完善与变更,以及多路径效应是造成测站虚假的非线性位移的另一个主要因素[11, 22]。因此,应分析造成这种现象的各种成因,分别对其建立相应的精确数学模型,并优化数据处理模型和策略,以减弱甚至消除由技术系统误差造成的影响,以便提取更准确干净的时间序列。
3.1.2 其他非线性变化的处理除季节性非线性变化外,测站坐标时序中还含有地震或天线更换引起的不连续变化、各种噪声造成的非线性变化。
目前,IGS基准站监测数据表明,至少有一半以上的测站坐标时间序列都不连续,这种不连续性的存在影响了其在地球动力学研究中的应用,也引起了国际上的广泛关注。在众多学者的不懈努力下,在ITRF2014的非线性运动建模中首次以测站振幅时间函数的形式给出了震后形变模型(见式(1)、式(2)),这将使均一化时间序列和高质量的地球动力学研究数据的获取成为可能,并进一步提高测站非线性运动建模的精度,进而实现毫米级国际地球参考框架的维持与更新。
研究表明,GPS位置坐标时间序列噪声不仅包含白噪声,其中还有与时间相关的有色噪声(如闪烁噪声、随机漫步噪声等),这其中个别噪声对基准站坐标的影响甚至可达厘米量级[20-21]。由于噪声对测站坐标时序的影响与其所处的地理环境有关,因此应采用极大似然估计和噪声频谱分析的方法来确定最适合各区域的噪声模型及噪声的特性,以将噪声与真实信号准确地分离。目前,噪声模型的建立忽视了水平和高程分量之间的相关性,将来可引入三维交互相关性方法,量化水平及高程方向的相互作用的程度,以构建精确的三维噪声模型[13]。
3.2 多技术数据组合算法目前,多技术实测数据联合处理存在两个关键问题:一是同种技术之内的组合,即以某种技术所得实测数据为基础进行解算,并给出统一解;二是不同技术之间的组合,即采用包含坐标、方差-协方差阵和先验约束等信息在内的SINEX文件作为输入数据,通过重构法方程与法方程叠加来实现多技术之间的组合[2]。
为了完善多技术数据组合算法,可基于紧组合方式,改进技术内组合数据处理软件,以获取同种技术内测站坐标时间序列精确的组合解。同时,深入分析研究技术间组合的输入/输出标准,不同技术系统误差的处理与定权方式,以及组合解算策略和模型精化,以提高并置站与局部连接精度及可靠性,从多技术组合算法上改进技术间组合方法[13]。在此多技术数据组合算法改进的基础之上,将可获得高精度测站的历元坐标。
3.3 地心运动的监测与建模根据IERS协议,国际地球参考框架的原点为包括海洋和大气在内的地球质量中心,它也是地球卫星绕其旋转的动力学中心。地球的质心运动来自地球各圈层的物质运动, 因此具有明显的地球物理机制, 特别是全球大气、海洋和地表水的季节性变化是地球质心周年运动的主要地球物理机制[18-19]。故而可利用这些地球物理因素的季节性变化的拟合模型对地球质心的周期运动进行建模分析。
一般情况下,GPS、SLR、DORIS空间大地测量技术都可用来监测地球质心的运动,但须考虑GPS、DORIS观测技术的复杂性和存在诸如天线相位中心的不确定性、抗模型误差能力较弱等问题。鉴于此,ITRF2014在地心运动建模中,最好只利用SLR技术进行建模,但是难以在短期内解决SLR测站全球分布不均匀的问题,因此需更好地优化基于SLR技术确定地心的算法与模型,并提升硬件质量以对地心运动进行精确建模[9-10]。为提高地心运动观测质量,可在原有激光动力学卫星观测的基础之上,联合CHAMP、GRACE等低轨地球卫星的新监测手段,为地球质心运动的监测提供更多源的实测数据。文献[20-21]分别利用CHAMP、GRACE卫星实测数据分析地球质心运动的周期运动特性,并给出了比较可靠的分析结果。基于上述监测技术、算法模型的改进,以及时间序列跨度的增加与数据观测质量的提高,将为毫米级精度的地心运动建模提供可能。
4 结语为了满足高精度全球形变监测以及地球动力学的科研需要,建立顾及测站非线性变化的毫米级国际地球参考框架势在必行。本文通过简要介绍国际地球参考框架最新研究进展,并对毫米级国际地球参考框架的建立方法及技术改进提出少许见解,希望为参考框架的维持与更新提供有益的参考。
| [1] | ALTAMIMI Z, SILLARD P, BOUCHER C. ITRF2000: A New Release of the International Terrestrial Reference Frame for Earth Science Applications[J]. Journal Geophysical Research, 2002, 107(B10): 1–19. |
| [2] | 刘经南, 魏娜, 施闯. 国际地球参考框架(ITRF)的研究现状及展望[J]. 自然杂志, 2013, 35(4): 243–250. |
| [3] | 门葆红, 董文亮, 孙付平, 等. 国际地球参考框架建立与维持的研究进展[J]. 测绘科学, 2016, 41(2): 20–25. |
| [4] | PEIT G, LUZUM B. The IERS Conventions(2010)[M]. Frankfurt: Verlagdes Bundesamts für Kartographie and Geodäsie, 2010. |
| [5] | ALTAMIMI Z, COLLILIEUX X, METIVIER I. ITRF2008: An Improved Solution of the International Terrestrial Reference Frame[J]. Journal of Geodesy, 2011, 85(8): 457–473. DOI:10.1007/s00190-011-0444-4 |
| [6] | SEITZ M, ANGERMANN D, BLOβFELD M, et al. 2014 ITRS Realization of DGFI: DTRF2014[C]//EGU General Assembly Conference. Vienna: EGU, 2015. |
| [7] | 成英燕. ITRF2008框架简介[J]. 大地测量与地球动力学, 2012, 32(1): 47–50. |
| [8] | TORNATORE V, KAYIKÇ E T, ROGGERO M. Analysis of GPS, VLBI and DORIS Input Time Series for ITRF2014[R]. [S.l.]: Publications on Research Gate, 2016. |
| [9] | SPATAR C B, MOORE P, CLARKE P J. Collinearity Assessment of Geocentre Coordinates Derived from Multi-satellite SLR Data[J]. Journal of Geodesy, 2015, 89(12): 1197–1216. DOI:10.1007/s00190-015-0845-x |
| [10] | ALTAMIMI Z, REBISCHUNG P, COLLILIEUX X, et al. ITRF 2014 Status, data Analysis and Results[C]//EGU General Assembly 2015. [S.l.]: EGU, 2015. |
| [11] | 姜卫平, 李昭, 刘万科, 等. 顾及非线性变化的地球参考框架建立与维持的思考[J]. 武汉大学学报(信息科学版), 2010, 35(6): 665–669. |
| [12] | 宋淑丽, 朱文耀, 熊福文, 等. 毫米级地球参考框架的构建[J]. 地球物理学报, 2009, 52(11): 2704–2711. |
| [13] | 姜卫平, 马一方, 邓连生, 等. 毫米级地球参考框架的建立方法与展望[J]. 测绘地理信息, 2016, 41(4): 1–6. |
| [14] | IERS. ITRF2013 Call for participation [EB/OL]. [2016-10-11]. http://itrf.ign.fr/ITRF_solutions/2013/CFP-ITRF2013-27-03-2013.pdf, 2013. |
| [15] | BACHMANN S, MESSERSCHMITT L, THALLER D. IVS Contribution to ITRF2014[M]. [S.l.]: Springer Berlin Heidelberg, 2015: 1-6. |
| [16] | COLLILIEUX X, VAN DAM T, RAY J, et al. Strategies to Mitigate Aliasing of Loading Signals While Estimating GPS Frame Parameters[J]. Journal of Geodesy, 2012, 86(1): 1–14. DOI:10.1007/s00190-011-0487-6 |
| [17] | TREGONING P, WATSON C. Atmospheric Effects and Spurious Signals in GPS[J]. Journal of Geophysical Research (Solid Earth), 2009, 114(B9): 5493–5511. |
| [18] | DONG D N, YUNEK T, HEFLIN M. Origin of the International Terrestrial Reference Frame[J]. Translated World Seismology, 2007, 108(4): 283–299. |
| [19] | CHEN J L, WILSON C R, EANES R J, et al. Geophysieal Interpretation of Observed Geocentre Variations[J]. Journal of Geographysical Research (Solid Earth), 1999, 104(B2): 2683–2690. DOI:10.1029/1998JB900019 |
| [20] | 蒋志浩, 张鹏, 秘金钟, 等. 顾及有色噪声影响的CGCS2000下我国CORS站速度估计[J]. 测绘学报, 2010, 39(4): 355–363. |
| [21] | LANGBEIN J. Noise in GPS Displacement Measurements from Southern California and Southern Nevada[J]. Journal of Geophysical Research(Atmospheres), 2008, 113(5): 620–628. |
| [22] | RAY J. Systematic Errors in GPS Position Estimates[C]//Presentation at IGS 2006 Workshop. Darmstadt: IGS, 2006. |


