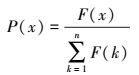2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
瓦片数据模型是一种受到广泛应用的影像数据模型,其基本思想是将一幅遥感影像按指定的网格大小均匀划分,从而得到一组瓦片数据集[1-3]。通过服务器来发布和管理瓦片数据,是目前对海量遥感影像数据进行组织与管理的主要方式[4-7]。
随着网络技术的快速发展,对等网络传输技术利用大量的客户端资源来分担服务器的压力,不但有效地降低了系统对服务器的依赖程度,提高了系统的稳定性,还极大地提高了数据分发传输的效率。对等网络传输技术为海量遥感影像数据的高效共享开辟了一条新的途径。
在对等网络中,当需求某一影像数据时,既可以从服务器端下载影像数据,也可以选择从其他终端中获取影像数据。这种方式既降低了客户端对服务器的依赖性,也提高了数据传输效率。与服务器不同,对等网络中各终端存储的数据各不相同,不同的终端可能存储着不同的瓦片数据。在对等网络中,当某一终端需要下载某一组瓦片数据时,选择从哪些终端下载哪些瓦片以提高传输效率,是一个需要解决的重要问题。
在给定的多个终端及多个候选影像瓦片资源中,如何选择从其中的某些终端下载某些瓦片,使得在获取全部被需求瓦片的条件下,使传输耗时最短,是一个组合优化问题。组合优化问题是指在离散的、有限的数据结构上及给定的约束条件下寻找目标函数最优解的问题,在规划调度、资源分配、决策等问题中有着非常广泛的应用[8-9]。典型的组合优化问题有旅行商问题[10-13]、背包问题等。当问题规模较小时,应用枚举法等常规方法就可以得到较好的可行解,但当问题规模较大时,解空间过大,常规方法已经无法适用。为了能够求解较大规模问题下的最优解,许多智能优化算法如蚁群算法、遗传算法、模拟退火算法等开始逐步应用于组合优化问题中。
遗传算法(genetic algorithm)是众多求解方法中非常有效的一种。遗传算法是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程、按照适者生存和优胜劣汰原理搜索最优解的方法[5-15]。遗传算法的优点在于其搜索覆盖面大,有利于全局择优且具有可扩展性,容易与其他算法结合。
遗传算法的运算对象是基因型--表示个体的符号串,进行遗传算法择优的基础是进行基因设计,即实现表现型到基因型的映射即编解码工作。遗传算法的基本运算过程如下:
(1) 初始化:设置终止进化的条件,随机生成M个个体作为初始群体P (0)。
(2) 适应度计算:计算群体P (t)中各个个体的适应度。
(3) 选择运算:根据个体适应度,选择交配双方,适应度越高,被选中的概率也越高,即物竞天择。
(4) 交叉运算:交配过程中父母双方基因产生交叉。
(5) 变异运算:将子代个体的某些基因值作变动。
(6) 新群体产生:群体P (t)经过选择、交叉、变异运算之后得到子群体P (t+1)。
(7) 终止进化:触发终止条件后终止计算,种群停止进化,以进化过程中所得到的具有最大适应度个体作为最优解输出。
1 瓦片资源遗传选择算法 1.1 基因设计基因的编码方法必须能够覆盖问题的所有可行解,本文采用字符编码的方式对表现型进行编码:一个字符唯一对应一个瓦片资源,一个瓦片资源唯一对应一个字符。表现型与基因型通过编码方式与解码方式相互转换。编码方式详细说明如下。
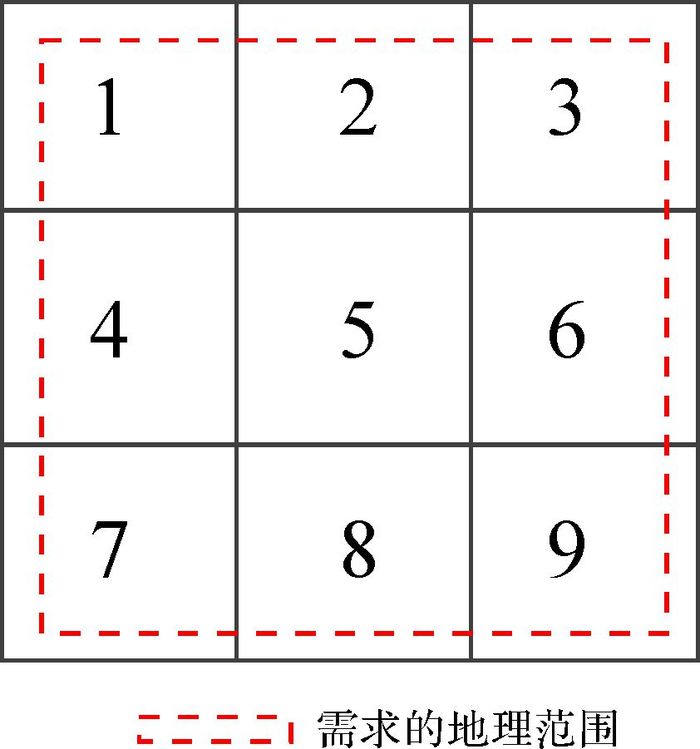
如图 1所示,假设落在需求范围内的瓦片共有9个,依次编号为1至9。某终端存储有编号为1、3、9的瓦片资源,选择某一瓦片则对应字符为1,否则为0。如果选择下载编号为1、9的瓦片资源、不选择编号为3的瓦片资源,那么此终端对应的字符串即基因片段为101。基因型编码示例见表 1。
|
| 图 1 落在需求范围内的瓦片数据 |
适应度是遗传算法中最关键的一个参数。在生物学中,适应度表示个体对环境的适应能力,是用来评判群体中个体的优劣程度,适应度越高,其繁衍后代的能力也越强。适应度反映了一个基因序列被选中的概率,适应度越高,其被选中的概率也越高。
瓦片资源选择目标是在保证覆盖全部需求范围的条件下使传输耗时尽可能短。本文基于各终端的历史传输速度,以多线程传输的方式从各个终端下载瓦片数据,在不考虑带宽限制的情况下,传输总耗时等于需求终端对各终端中的最大传输耗时。传输总耗时计算方法见表 2,“…”表示数据根据实际选择而变化,其值不唯一;历史平均传输速度通过查询各终端历史传输速度表数据并进行计算得来;各终端传输耗时通过被选瓦片的总数据量除以历史平均传输速度而得。
| 终端A | 终端B | 终端C | |
| 瓦片存储 | 1、3、9 | 2、3、5 | 1、5、6、7、8 |
| 选择的瓦片 | … | … | … |
| 被选瓦片的总数据量 | … | … | … |
| 基因 | … | ||
| 历史传输平均速度 | v1 | v2 | v3 |
| 传输耗时 | t1 | t2 | t3 |
| 传输总耗时T | T=max[t1, t2, t3, …, tn] | ||
| 求解目标 | 在保证覆盖全部需求范围的情况下使T最小,求解每个终端所选瓦片编号集:{(…),(…),…,(…)} | ||
根据求解目标,适应度函数初步设计为
F (x)=covRatio·(max[t1, t2, t3, …, tn]-tx)
式中,covRatio表示选择的不同瓦片个数与需求的不同瓦片总数之间的关系:当选择的不同瓦片个数等于需求的不同瓦片总数,则covRatio=1,反之covRatio=0,适应度也会等于零,表示此基因个体被淘汰。covRatio参数的设计主要是为了保证能够下载所有被需求的不同瓦片资源。
max[t1, t2, t3, …, tn]-tx中,tx表示种群中第x个基因对应的数据传输时间,x=1, 2, …, n。max[t1, t2, t3, …, tn]-tx表示种群中各基因数据传输时间中的最大数据传输时间减去每一个基因个体对应的数据传输时间。基因个体对应的数据传输时间越短,此基因个体的适应度越高。显然此参数会直接淘汰掉数据传输时间最长的那个基因个体,因此可以加快种群的进化速度。
同时,max[t1, t2, t3, …, tn]-tx的参数形式也表明,基因个体的适应度是相对于种群中其他基因个体而言的,即此适应度是相对适应度,因此隔代基因个体之间无法通过适应度判断其相对好坏。在遗传算法计算中,系统无法单独计算每一个基因个体的适应度,必须要以群体为单位进行相对适应度计算,每进行一轮交配繁衍,需要重新对群体中各基因个体的适应度进行计算。
此外,当种群中基因个体对应的数据传输时间全部相同时,max[t1, t2, t3, …, tn]-tx的值会变为零,因此适应度也会变为零。由于适应度为零的基因个体不会被选中去进行交配繁殖,因此为了保证种群能够继续进化,当种群中基因个体对应的数据传输时间全部相同时,所有的基因个体的适应度设为最大数据传输时间。
最后,max[t1, t2, t3, …, tn]-tx的参数形式并不能保证去掉所有的重复数据选择,因此还需要对遗传算法得出的最优解继续进行去重,以保证最终的结果不会重复下载相同的瓦片。
最终,适应度函数设计为:
当种群中各基因个体对应的数据传输时间不尽相同时
F (x)=covRatio·(max[t1, t2, t3, …, tn]-tx)
当种群中各基因个体对应的数据传输时间全部相同时
F (x)=covRatio·t
式中,当选择的不同瓦片个数等于需求的不同瓦片总数时,则covRatio=1,反之covRatio=0。
1.3 遗传选择算法计算过程瓦片数据选择的遗传算法操作过程为:
(1) 初始化:设置最大进化次数T=20,随机生成20个互不相同的基因个体作为初始群体P (0)。
(2) 适应度计算:开始繁殖与进化,计算群体中每一个基因个体的适应度。
(3) 选择运算:首先根据每个基因个体的适应度计算其被选中的概率
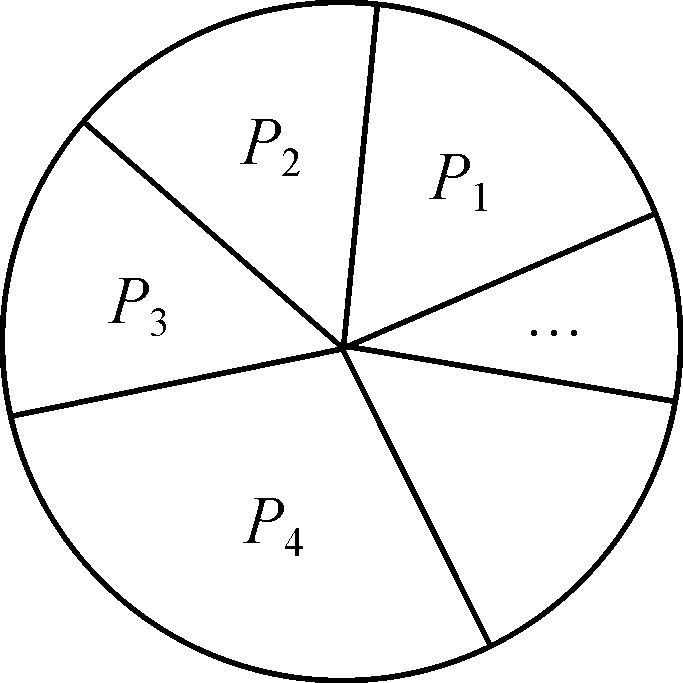
然后以轮盘赌的方式选择交配的双方,如图 2所示,基因个体的适应度越高,其在轮盘上的面积越大,被选中的概率也就越大。
|
| 图 2 轮盘赌 |
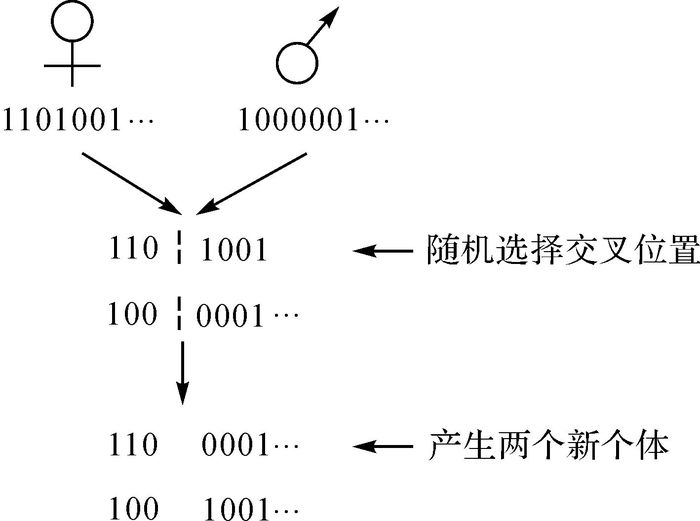
(4) 交叉运算:如图 3所示,交配双方进行交配,双方基因产生交叉,交叉位置随机。
|
| 图 3 交叉运算 |
(5) 变异运算:对新个体,随机选取变异点,变异点值为0则变1,为1则变0,变异概率p设为0.2%。例如,新基因个体1100001,变异点位置5,变异后基因为1100101。
(6) 产生新群体:对群体中重复步骤(3) ~(5),采用精英主义将上一代中适应度最高的基因个体直接保留进入下一代。对群体经过选择、交叉、变异运算之后得到下一代群体。
(7) 终止:新群体继续产生新群体:对新群体继续执行群体进化操作。当群体进化次数达到最大进化次数T,则最终群体中所得到的具有最大适应度个体作为最优解输出,终止计算。
(8) 最优解去重:由于遗传算法得出的最优解并不能保证去掉所有的重复数据下载,因此还需要对遗传算法得出的最优解继续进行去重,以保证最终的结果不会重复下载相同的瓦片。
2 试验与结果分析 2.1 测试数据测试数据集为:模拟10个终端,落在需求范围内的不同瓦片总个数为9,每个瓦片大小为1 MB,种群规模100,群体进化20次。瓦片分布见表 3,下载全部不同瓦片的最短传输时间为0.4 s,最长传输时间为3 s。
| 终端 | 瓦片编号 | 传输速度/(MB/s) |
| Terminal1 | 1、3、6 | 1 |
| Terminal2 | 1、2、3、6 | 5 |
| Terminal3 | 2、4 | 2 |
| Terminal4 | 6 | 3 |
| Terminal5 | 2、7、9 | 10 |
| Terminal6 | 5、8 | 9 |
| Terminal7 | 7 | 6 |
| Terminal8 | 4、6、8、9 | 7 |
| Terminal9 | 5、9 | 3 |
| Terminal10 | 8 | 8 |
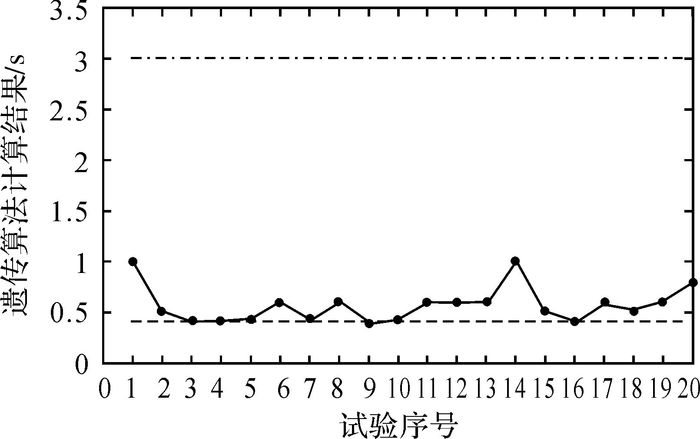
重复进行20次试验,结果如图 4所示:上方虚线表示所有可行解中数据传输耗时的最大值(3 s),下方虚线表示所有可行解中数据传输耗时的最小值(0.4 s)。从图中可以看出,遗传算法计算结果相对较好,数据传输耗时比较接近于0.4 s的最佳结果,而且结果波动较小,验证了遗传算法在瓦片资源选择上的有效性。
|
| 图 4 遗传选择算法的计算结果 |
遗传算法未采取精英主义时,在种群迭代过程中种群可能会发生如图 5所示的退化现象,如同自然界中某些动植物群体的退化一样,而且种群的进化速度比较慢,甚至是没有进化。为了避免出现这种情况,在遗传算法计算过程中采取精英主义,将上一代中适应度最高的基因个体直接保留进入下一代。

|
| 图 5 种群退化现象 |
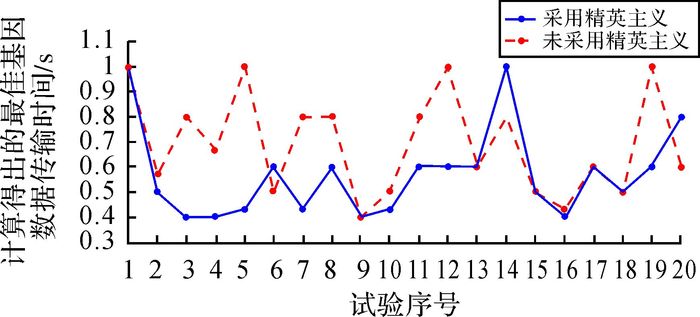
对未采用精英主义的遗传算法与采用精英主义的遗传算法分别重复进行20次试验,试验结果对比见表 4及如图 6所示,可以看出,采用精英主义之后,遗传算法计算结果的质量有了明显的提升,均值降低了17.3%左右,方差也有所降低。
|
| 图 6 采用与未采用精英主义的遗传算法计算结果对比图 |
本文研究如何提高对等网络环境中瓦片影像数据的共享效率,在有效利用对等网优势的基础上,提出了一种基于遗传算法的瓦片资源选择方法。试验结果表明,这一方法可以有效地解决瓦片资源选择这类组合优化问题,具有一定的实际应用价值。
| [1] | 霍亮, 杨耀东, 刘小勇, 等. 瓦片金字塔模型技术的研究与实践[J]. 测绘科学, 2012, 37(6): 146–148. |
| [2] | 贲进, 童晓冲, 张衡, 等. 基于TIFF和XML标准的瓦片金字塔模型[J]. 测绘科学技术学报, 2005, 22(3): 184–186. |
| [3] | 周强, 宋志峰, 刘易鑫, 等. 一种适用于多移动终端的地图瓦片格式的研究与应用[J]. 测绘与空间地理信息, 2013(S1): 70–76. |
| [4] | 郭明强, 黄颖, 谢忠. 分布式环境下海量瓦片数据实时组织与调度策略研究[J]. 测绘通报, 2013(4): 25–28. |
| [5] | 李治庆, 马照亭, 李成名, 等. 3DGIS海量瓦片数据管理与调度[J]. 测绘科学, 2013, 38(6): 109–110. |
| [6] | 商秀玉. WebGIS海量瓦片数据管理引擎的设计与实现[D]. 金华: 浙江师范大学, 2012. http://d.wanfangdata.com.cn/Thesis/Y2193715 |
| [7] | 刘小生, 吴征, 王永生. 一种海量遥感影像实时切割与高效调度新方法[J]. 测绘科学技术学报, 2013, 30(1): 51–53. |
| [8] | 马立肖, 王江晴, XIAOMali, 等. 遗传算法在组合优化问题中的应用[J]. 计算机工程与科学, 2005, 27(7): 72–73. |
| [9] | 汪松泉. 遗传算法在组合优化中的应用研究[D]. 合肥: 安徽大学, 2010. |
| [10] | 高经纬, 张煦, 李峰, 等. 求解TSP问题的遗传算法实现[J]. 计算机时代, 2004(2): 19–21. |
| [11] | NOZARIAN S, DEHGHAN Y, JAHAN M V. Solving TSP on the Basis of Grid and Genetic Algorithm[J]. International Proceedings of Computer Science & Information Tech, 2012, 34: 61–66. |
| [12] | 于莹莹, 陈燕, 李桃迎. 改进的遗传算法求解旅行商问题[J]. 控制与决策, 2014(8): 1483–1488. |
| [13] | SUN L. Genetic Algorithm for TSP Problem[C]//International Industrial Informatics and Computer Engineering Conference.[S.l.]:ACM 2015. |
| [14] | 于海璁, 陆锋. 一种基于遗传算法的多模式多标准路径规划方法[J]. 测绘学报, 2014, 43(1): 89–96. |
| [15] | 任海艳, 陈飞翔. 一种基于遗传算法的曲线化简方法[J]. 测绘通报, 2012(10): 32–35. |