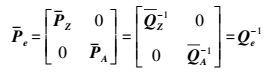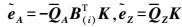三维激光扫描作为一种较新的数据获取技术,具有高精度、高效率、无接触、快速等优势,已成为数据获取的重要手段。其中如何利用点云数据建立精确三维模型是其应用的一个关键问题。国内外学者对点云建模进行了大量研究,并取得一些有益成果。点云拟合最初采用最小二乘法(LS),考虑系数矩阵含有误差,Colub H等提出了整体最小二乘方法[1](total least squares,TLS),后Schaffirin发表了带有等式约束的TLS方法[2];但整体最小二乘方法没有考虑数据不等精度问题,为解决此问题,Schaffrin提出在整体最小二乘基础上加入权阵的加权整体最小二乘迭代方法(weighted total least squares,WTLS)[3],较好地解决了变量不等精度的整体最小二乘问题。在三维激光扫描领域,后续研究者也进行了深入研究[4-7]。陈玮娴提出了根据点云激光反射强度及对系数阵A列向量部分修正引入权阵的加权整体最小二乘法,很好地解决了平面靶标和球面靶标拟合问题[8];苍桂华提出了入射角定权的加权总体最小二乘平面拟合方法[9],获得较高拟合精度。但这些方法均没有考虑观测数据含有异常值情况,因此,需采用更为稳健的参数估计方法。龚循强提出了基于IGG权函数的稳健加权总体最小二乘方法,获得了更可靠、更优参数估值[10];王彬提出了抗差加权整体最小二乘的牛顿-高斯算法,此算法利用标准化残差进行检验量的构建,并利用中位数法获取单位权中误差估值,具有很好抗差性[11]。然而,以上抗差方法目前鲜有应用到三维激光领域,因此,针对三维激光扫描点云数据拟合中数据不等精度及含有异常值的问题,在结合抗差整体最小二乘及入射角定权方法基础上,本文提出基于三维激光扫描点云数据的抗差加权整体最小二乘方法。此方法采用点云数据入射角余弦值cos θ作为拟合的权重,利用标准化残差构造权因子函数,利用中位数法获得单位权中误差估值,并应用于三维激光扫描平面、耙球的拟合,经实例证明此方法可以有效解决点云数据含有粗差及不等精度拟合问题。
1 抗差加权整体最小二乘 1.1 函数模型及基本原理由于地面三维激光现实扫描场景中含有大量平面特征及激光靶标多为平面球面,因此本文以平面和球面为例。
对于空间平面点云数据,方程式为
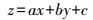 (1)
(1) 式中,a、b、c为待求的平面拟合参数;x、y、z为平面点云数据三维坐标。
将平面方程写成矩阵形式
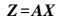 (2)
(2) 式中
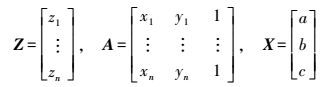 (3)
(3) 对于球面,方程为
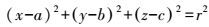 (4)
(4) 式中,a、b、c为球心坐标;x、y、z为球面点云数据三维坐标;r为球半径。球面方程展开式为
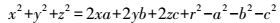 (5)
(5) 将x2+y2+z2、2x、2y、2z看作新的观测值,a、b、c、r2-a2-b2-c2看作新的参数,可写成矩阵形式
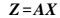 (6)
(6) 式中
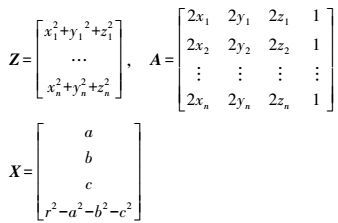 (7)
(7) 同时顾及观测向量Z和系数矩阵A的误差,建立EIV模型
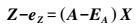 (8)
(8) 相应的随机模型为
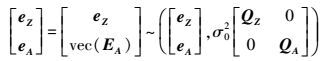 (9)
(9) 式(8) 中,Z为m×1维的观测向量;A为m×n维的系数矩阵;eZ、EA分别为观测向量和系数矩阵的随机误差矩阵;X为n×1维未知数参数向量。式(9) 中, vec表示列向量化,是将矩阵从左到右按列拉直;σ02是验前单位权方差;QZ、QA分别为观测向量和系数矩阵的协因数阵。考虑观测向量Z和系数矩阵A存在粗差,本文采用式(10) 作为估计准则
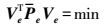 (10)
(10) 式中
其中,PZ、PA分别为观测向量和系数阵的等价权阵,QZ、QA为对应等价协因数阵。协因数阵Qe(QZ,QA)计算公式为
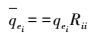 (11)
(11) 式中,i为观测值序号,限制条件为对应的先验协因数不为零;Rii为相应权因子倒数;qei、qei分别为Qe、Qe对应位置的元素。
其中权因子函数Rii计算公式如下
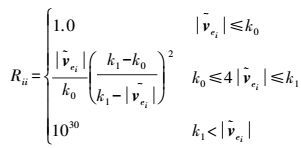 (12)
(12) 式中,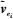
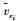
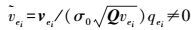 (13)
(13) 式中,σ0为单位权中误差;vei表示残差向量Ve的第i个元素;Qvei表示残差协因数阵Qve第i个元素。由于传统的计算公式获得的σ0的估值受粗差的影响较大,本文采用中位数法获得具有抗差性的单位权中误差估值
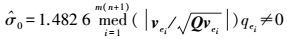 (14)
(14) 根据协因数传播率得
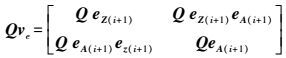 (15)
(15) 在三维激光扫描点云拟合中,由于点云数据是不等精度观测,本文根据各点精度确定权值,相关文献提出点云数据入射角越小,其点位精度越高[6-7],其权值越大,因此本文引入入射角余弦值作为权重。平面点云数据观测点权值为
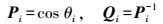 (16)
(16) 式中,Pi为观测点权值;θi为i点入射角。
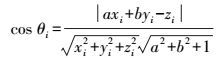 (17)
(17) 式中,(a,b,-1) 为拟合平面法向量;xi、yi、zi含义同式(4)。同理,推出球面点云观测点入射角余弦值为
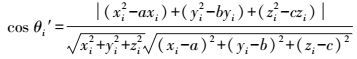 (18)
(18) 式中,(xi-a,yi-b,zi-c)为拟合球面法向量;xi、yi、zi含义同式(4)。
1.3 Gauss-Neuton迭代算法设第i次迭代计算后,所得参数估值为X(i),预测残差矩阵为EA (i)。
由于EIV模型是非线性的,将式(8) 在(X(i), EA (i))处线性化展开,保留一阶导数项,过程如下
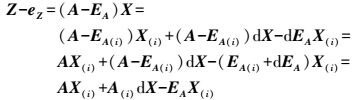 (19)
(19) 转换并移项得
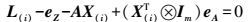 (20)
(20) 式中,A=A(i)+EA(i);X=X(i)+dX; EAX(i)=(X(i)T⊗Im)eA;L(i)=Z-AX(i);dX为拟合参数微小改正值;Im为m×m单位阵(“⊗”为kronecker积)。
结合EIV模型估计准则,构造拉格朗日目标函数
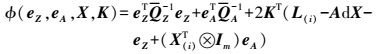 (21)
(21) 根据Eular-Lagrange必要条件对变量eZ、eA、dX、K求导并令其等于零,有
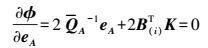 (22)
(22) 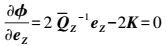 (23)
(23) 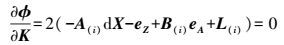 (24)
(24) 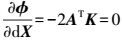 (25)
(25) 式中,B(i)=X(i)T⊗Im。将式(22) 和式(23) 整理得
代入式(22) 得
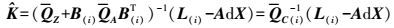 (26)
(26) 式中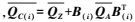
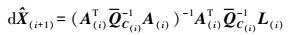 (27)
(27) 迭代步骤如下:
(1) 设置初值,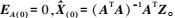
(2) 根据式(17)、式(18) 分别计算平面和球面各点余弦值,组成相关权阵及协因数阵。
(3) 从i=0开始依次计算
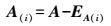 (28)
(28) 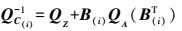 (29)
(29) 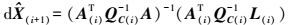 (30)
(30) 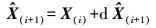 (31)
(31) 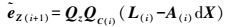 (32)
(32) 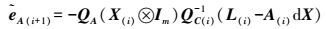 (33)
(33) (4) 重复步骤(3) 直至满足||dX(i+1) || < ε0(ε0为事先给定的小正数)时,迭代停止。
(5) 将WTLS迭代获得的参数估值和残差向量作为初值,将第k-1次迭代获得的参数估值和残差向量,以及先验协因数阵QZ、QA代入式(15) 更新相应残差协因数阵,再将残差向量和残差协因数阵代入式(13) 和式(14) 获得第k次迭代标准化残差。
(6) 利用式(12) 和式(13) 更新等价协因数阵,从而获得第k+1次参数估值和残差向量。
(7) 重复步骤(5) 和(6),直到满足||dX(i+1) || < ε0(ε0为事先给定的小正数)迭代终止。
2 算例分析 2.1 仿真数据试验为验证算法可行性,首先用仿真数据进行试验。以平面为例,设拟合平面方程为z=x+2y+1,给定参数真值为:a=1,b=2,c=1。在Matlab中在坐标(xi, yi, zi)上加入均值为u=0,方差为σ2=1/100×cos θi的随机误差(其中i表示点号,θi表示入射角余弦值),从中任取选取30个点,得到一组模拟点云数据。
在模拟数据中加入位置随机产生的粗差,其绝对值一般介于标准差的10~30倍之间。设计方案如下:加入粗差前分别进行加权整体最小二乘(WTLS)和抗差加权整体最小二乘(RWTLS)估计,然后分别加入1、2、3个粗差,比较两种方法参数估计结果,见表 1。
| 粗差个数 | 算法 | 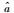 | 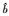 | 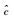 | max (da) | max (db) | max (dc) |
| 真值 | 1 | 2 | 1 | - | - | - | |
| 0 | WTLS | 1.000 0 | 2.000 0 | 1.001 2 | 0.000 0 | 0.000 0 | 0.001 2 |
| RWTLS | 1.000 0 | 2.000 0 | 1.001 2 | 0.000 0 | 0.000 0 | 0.001 2 | |
| 1 | WTLS | 0.981 2 | 2.061 4 | 1.033 7 | 0.018 8 | 0.061 4 | 0.033 7 |
| RWTLS | 1.000 0 | 2.000 0 | 1.016 4 | 0.001 3 | 0.002 2 | 0.016 4 | |
| 2 | WTLS | 1.054 9 | 1.951 4 | 1.089 6 | 0.054 9 | 0.145 6 | 0.089 6 |
| RWTLS | 1.000 0 | 2.000 0 | 1.016 4 | 0.003 6 | 0.007 7 | 0.016 4 | |
| 3 | WTLS | 0.954 5 | 2.168 6 | 1.193 4 | 0.142 6 | 0.168 6 | 0.193 4 |
| RWTLS | 1.000 0 | 2.000 0 | 1.016 4 | 0.059 5 | 0.122 1 | 0.084 0 |
表 1中max (da)、max (db)、max (dc)分别为da、db、dc的最大拟合参数估值与真值差。
由表 1可看出:当没有粗差时,RWTLS方法与WTLS方法精度相同,均获得较高精度参数解;当含粗差时,RWTLS方法拟合参数估值与真值差明显小于WTLS,且与不含粗差时精度相当,参数估值准确度较高。
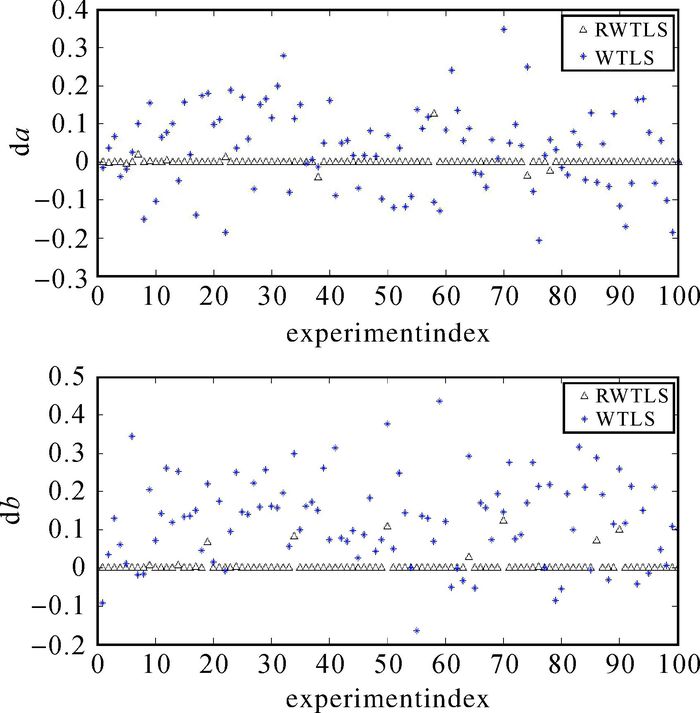
为直观比较两种方法的参数拟合准确性,在粗差为3时进行100次模拟,比较100次模拟两种方法da、db差值序列,结果如图 1所示。
|
| 图 1 粗差个数为3时WTLS和RWTLS参数差值序列 |
由图 1可看出,RWTLS获得的参数差值较WTLS小、更接近真值。
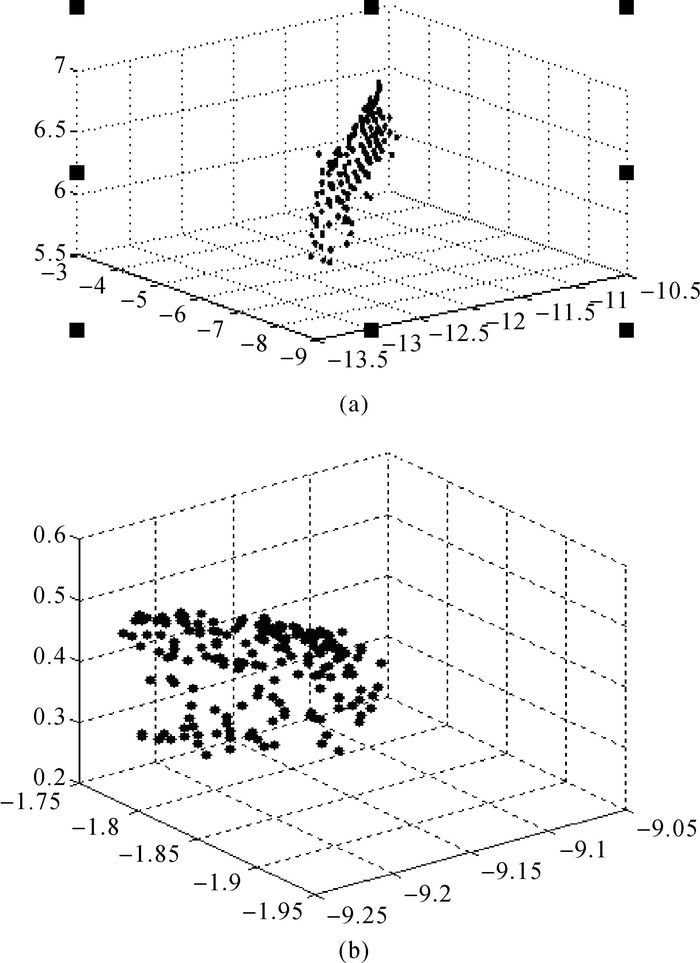
2.2 实测数据试验为进一步验证算法准确性,采用实测数据并加入抗差整体最小二乘方法(RTLS)进行计算。试验采用中海达LS300三维激光扫描仪对某校测绘学院红楼和布设球靶标(半径为0.072 5 m)的学校罗马柱广场进行扫描,得到平面和球面点云数据,从中选取平面和球面数据,手动删除大量冗余点,得到如图 2点云数据,各选取50个点进行试验,方案同上,参数拟合结果见表 2、表 3。
|
| 图 2 平面和球面靶标点云数据 |
| 粗差个数 | 算法 | 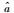 | 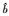 | 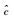 | 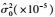 |
| 0 | WTLS | 72.889 9 | -40.048 4 | 629.203 1 | 0.133 7 |
| RTLS | 72.505 3 | -39.836 0 | 625.914 7 | 0.343 7 | |
| RWTLS | 72.889 9 | -40.048 4 | 629.203 1 | 0.133 7 | |
| 1 | WTLS | 74.809 3 | -41.134 4 | 645.381 4 | 0.514 2 |
| RTLS | 72.810 2 | -40.022 2 | 628.336 5 | 0.231 7 | |
| RWTLS | 72.816 7 | -40.005 7 | 628.599 1 | 0.131 4 | |
| 2 | WTLS | 76.342 9 | -41.915 8 | 659.182 8 | 2.263 5 |
| RTLS | 72.803 8 | -40.025 4 | 628.276 3 | 0.210 6 | |
| RWTLS | 72.863 5 | -40.057 2 | 628.733 3 | 0.154 7 | |
| 3 | WTLS | 82.609 5 | -45.238 2 | 714.451 9 | 2.917 7 |
| RTLS | 73.344 1 | -40.318 8 | 632.904 9 | 0.364 0 | |
| RWTLS | 73.001 2 | -40.125 3 | 630.006 4 | 0.167 5 |
| 粗差个数 | 算法 | 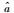 | 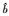 | 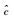 | r2-(a2+b2+c2) | 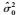 | dr2 |
| 0 | WTLS | -9.248 2 | -1.859 6 | 0.447 1 | -89.180 3 | 7.938 2×10-9 | 0.001 5 |
| RTLS | -9.252 8 | -1.861 1 | 0.447 3 | -89.269 7 | 1.176 7×10-8 | 0.002 2 | |
| RWTLS | -9.248 2 | -1.859 6 | 0.447 1 | -89.180 3 | 7.938 2×10-9 | 0.001 5 | |
| 1 | WTLS | -9.702 9 | -1.893 8 | 0.584 5 | -97.793 4 | 2.781 4×10-6 | 0.133 6 |
| RTLS | -9.253 9 | -1.860 7 | 0.448 1 | -89.289 8 | 9.509 2×10-9 | 0.002 3 | |
| RWTLS | -9.251 6 | -1.860 2 | 0.447 1 | -89.245 3 | 6.990 7×10-9 | 0.002 0 | |
| 2 | WTLS | -9.736 9 | -1.431 8 | 0.589 7 | -96.707 1 | 1.423 3×10-5 | 0.493 2 |
| RTLS | -9.252 1 | -1.860 6 | 0.447 1 | -89.256 | 1.156 2×10-8 | 0.002 1 | |
| RWTLS | -9.246 8 | -1.859 3 | 0.446 8 | -89.153 6 | 5.040 4×10-9 | 0.000 7 | |
| 3 | WTLS | -10.351 5 | -1.469 7 | 0.564 8 | -108.137 4 | 1.918 6×10-5 | 1.489 9 |
| RTLS | -9.252 0 | -1.860 9 | 0.447 5 | -89.254 6 | 1.051 2×10-8 | 0.002 2 | |
| RWTLS | -9.246 8 | -1.859 4 | 0.446 8 | -89.153 8 | 3.806 7×10-9 | 0.000 9 |
表中dr2为半径估值平方与真值差值。由表 2、表 3可看出,对于平面和球面拟合,当不含粗差时,RWTLS与WTLS方法精度高于RTLS方法,说明采用入射角定权方法可获得较高精度参数解;当含粗差时,WTLS拟合精度明显下降,参数解波动较大,且随着粗差个数的增加拟合精度越来越低,而RTLS方法和RWTLS方法拟合精度与不含粗差时相当,单位权中误差变化较小,优于WTLS方法,且RWTLS方法获得单位权中误差和半径平方差值比RTLS方法小,精度优于RTLS方法。
3 结语针对三维激光扫描数据常规拟合方法精度受粗差影响较大情况,本文结合抗差整体最小二乘和入射角定权方法提出一种以入射角定权的抗差加权整体最小二乘方法,解决了三维激光扫描点云数据拟合问题。理论推导和试验分析结果表明:
(1) 当数据不含粗差时,本文采用的RWTLS方法拟合精度高于RTLS方法,可以得出RWTLS方法采用的入射角定权方法可以提高拟合参数精度,从而获得较优参数解。
(2) 当数据含粗差时,WTLS方法拟合精度明显下降,且随着粗差个数的增加,WTLS拟合精度越来越低,而RWTLS和RTLS拟合精度几乎不变且与不含粗差时精度相当。
综上,以入射角定权的RWTLS具有较好抗差性和较高精度参数解,能够解决三维激光扫描点云拟合中数据含有异常值及不等精度问题。
| [1] | GOLUB H, AN LOAN CH. An Analysis of the Total Least Squares Problem[J]. SIAM Journal on Numerical Analysis, 1980, 17(6): 883–893. DOI:10.1137/0717073 |
| [2] | SCHAFFRIN B, US Y A. On Total Least-square Adjustment with Constraints[J]. IAG-Symp, 2005, 128: 417–421. |
| [3] | SCHAFFRIN B, IESER A. On Weighted Total Least-square Adjustment for Liner Regression[J]. Journal of Geodesy, 2008, 82(7): 415–421. DOI:10.1007/s00190-007-0190-9 |
| [4] | 王乐洋, 许才军, 鲁铁定. 病态加权总体最小二乘平差的岭估计解法[J]. 武汉大学学报(信息科学版), 2011, 35(11): 1346–1350. |
| [5] | AMIRI S, JAZAERI S. Weighted Total Least Squares Formulated by Standard Least Squares Theory[J]. Journal of Geodesy, 2012, 2(2): 113–124. |
| [6] | VIAHID M. On Weighted Total Least-squares for Geodetic Transformations[J]. Journal of Geodesy, 2012, 86(5): 359–367. DOI:10.1007/s00190-011-0524-5 |
| [7] | JAZAERI S, AMIRI S, SHARIFI M A. Iterative Algorithm for Weighted Total Least Squares Adjustment[J]. Survey Review, 2014, 46(334): 19–27. DOI:10.1179/1752270613Y.0000000052 |
| [8] | 陈玮娴, 陈义, 袁庆, 等. 加权总体最小二乘在三维激光标靶拟合中的应用[J]. 大地测量与地球动力学, 2010, 30(5): 90–96. |
| [9] | 苍桂华, 李明峰, 岳建平. 以入射角定权的点云数据加权总体最小二乘平面拟合研究[J]. 大地测量与地球动力学, 2014, 34(3): 95–98. |
| [10] | 龚循强, 李志林. 稳健加权总体最小二乘法[J]. 测绘学报, 2014, 43(9): 888–894. |
| [11] | 王彬, 李建成, 高井祥, 等. 抗差加权整体最小二乘模型的牛顿-高斯算法[J]. 测绘学报, 2015, 44(6): 602–607. DOI:10.11947/j.AGCS.2015.20130704 |
| [12] | 陈玮娴, 袁庆. 抗差总体最小二乘[J]. 大地测量与地球动力学, 2012, 32(6): 111–114. |
| [13] | 官云兰, 刘绍堂, 周世健, 等. 基于整体最小二乘的稳健点云数据平面拟合[J]. 大地测量与地球动力学, 2011, 31(5): 80–83. |
| [14] | 杨元喜. 抗差估计的概念和任务[J]. 测绘通报, 2004(4): 36–39. |
| [15] | 杨元喜, 宋力杰, 徐天河. 大地测量相关观测抗差估计理论[J]. 测绘学报, 2002, 31(2): 95–99. |
| [16] | 袁庆, 楼立志, 陈玮娴. 基于加权整体最小二乘的点云数据平面拟合法[J]. 测绘通报, 2011(3): 1–3. |