2. 陆航驻哈尔滨地区军代室, 黑龙江 哈尔滨 150000
2. Military Representative Office of Army Aviation in Harbin, Harbin 150000, China
计算机视觉使计算机通过二维图像认知三维环境信息,因此图像精度对计算机视觉十分重要。但实际镜头往往带有不同程度的畸变,并不是严格透视成像,为保证计算机视觉研究中产品的质量和精度,必须对获取图像进行畸变校正[1]。
目前,镜头畸变校正算法主要分为两类:第一类是摄像机标定法,将畸变参数和摄像机内外参数放在一起求解,在摄像机标定的过程中求解畸变参数。摄像机标定分为传统标定法[2-4]和自标定法[5-7]。传统摄像机标定方法精度高,可靠性好,但需要标定靶标,标定过程复杂。摄像机自标定方法不需要标定物,方法较灵活,但是多个参数一起校正必然会出现参数耦合问题,且对初值和噪声敏感,鲁棒性不强。第二类是非量测独立校正算法,可以不考虑其他内参的影响而直接校正畸变,因而引起大量学者的兴趣。学者们提出基于交比不变性[8-9]、基于直线投影[10-11]、基于消隐点共线约束[12]等方法来校正畸变,文献[13]构建了畸变分离模型,利用非量测的方法完成摄像机标定。但是以上这些算法都直接将平面几何中心作为像主点处理,而受限于制作工艺水平,主点坐标与平面几何中心往往存在差异。畸变具有其独立性,尤其镜头畸变的主要成分--径向畸变是与像主点坐标有关的函数,故基于已知摄像机中心假设前提,势必会影响畸变校正精度。文献[14]考虑到主点因素,利用遗传算法同时优化获取畸变参数和主点坐标,但算法计算成本过高,实现较困难。
因此,本文提出一种基于基本矩阵约束进行畸变自动校正的方法,同时对像主点坐标进行估计。根据基本矩阵约束建立关于基本矩阵、畸变参数、主点坐标的非线性模型,为使得求解过程稳定,求解时两类参量(基本矩阵与畸变参数、主点坐标)分步迭代进行,最终可实现两幅图像进行摄像机镜头畸变的稳健自动校正。
1 算法基本原理 1.1 对极几何对极几何是两视图之间内在的射影几何,它只依赖于摄像机内参数及相对姿态,与景物结构无关。如图 1所示,两摄像机分别由它们的中心C、C′表示;摄像机中心、三维点X及其像点x、x′都在对极平面π上;像点x反向投影成三维空间的一条射线,由摄像机中心C和x确定,这条射线在第二幅视图中成像为一条直线l′(对应x的对极线);由于三维空间点X必然在这条射线上,故X在第二幅视图中的像点x′必然在l′上。

|
| 图 1 对极几何 |
基本矩阵F是对极几何关系的核心,它是一个秩为2的3×3矩阵。若一个三维空间点X在两幅视图中的投影分别为x和x′,那么有基本矩阵约束
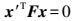 (1)
(1) 式中,x=[x y 1]T,x′=[x′ y′ 1]T,均为齐次坐标。
1.3 镜头畸变校正模型镜头畸变校正模型为
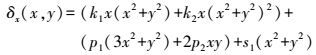 (2)
(2) 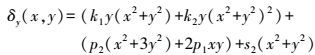 (3)
(3) 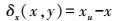 (4)
(4) 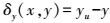 (5)
(5) 式(2) -式(3) 中,第一项为径向畸变;第二项为离心畸变;第三项为薄棱镜畸变;k1、k2、p1、p2、s1、s2为畸变系数。文献[15]已经证明非径向畸变的误差总和只有径向畸变的1/7~1/8,Tasi[2]也认为过多地考虑畸变会增加计算复杂程度,反而有可能会影响计算精度。故一般在应用中仅使用第一项径向畸变,而k2对畸变贡献较小,这里仅使用一阶径向畸变模型
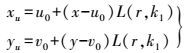 (6)
(6) 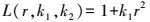 (7)
(7) 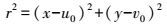 (8)
(8) 式中,(u0, v0)表示像主点坐标,即畸变中心。
2 算法实现 2.1 待求量参数化令(xu, x′u)表示两幅未畸变图像的同名点齐次坐标,根据对极几何关系,有
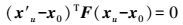 (9)
(9) 令(x, x′)表示实际两幅畸变图像的同名点齐次坐标,把镜头畸变校正模型(式(6))代入,即得到图像畸变情况下的对极几何关系式
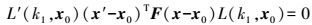 (10)
(10) 式中,x0=[u0, v0, 1];k1、u0、v0为待求参数;由于F是在存在畸变的情况下求解得到的,因此也是不精确的,这里把F也当作待求参数;x和x′为获取的同名像点,为已知量。因此,问题转化为已知同名点集,如何求解k1、u0、v0并优化修正F。待求参量过多时,容易造成解的不稳定,本文采用两步求解及分步迭代优化的分层策略,分别求解基本矩阵F和k1、u0、v0。采用RANSAC黄金标准算法估计两视图基本矩阵;用迭代最小二乘求解畸变系数和主点坐标,校正图像;两步求解交替进行,直至满足收敛条件。
2.2 参数平差模型建立与求解将式(10) 左边表示成多项式形式
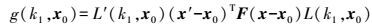 (11)
(11) 令x′-x0=[x′ y′ 1]T, x-x0=[x y 1]T, x0=[u0 v0 1]T, 易知,g ()为非线性函数。通过一阶泰勒展开,可获取函数g ()的线性误差方程形式为
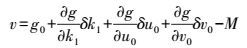 (12)
(12) 式中,g0为式(11) 的初始值;M为实际测量值,因为基于RANSAC鲁棒估计获取的内点都满足基本矩阵约束(式(1)),故M设为0;径向畸变系数k1一般赋初值为0;像主点坐标x0初值设为图像中心。
当有n组同名点时,可组成线性误差方程组
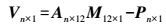 (13)
(13) 式中,M=[δk1 δu0 δv0]T,利用最小二乘平差原理,易得改正量的最优估计为
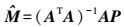 (14)
(14) 为保证精度,更新过程采取迭代方式进行,一般迭代2~3次即可收敛。
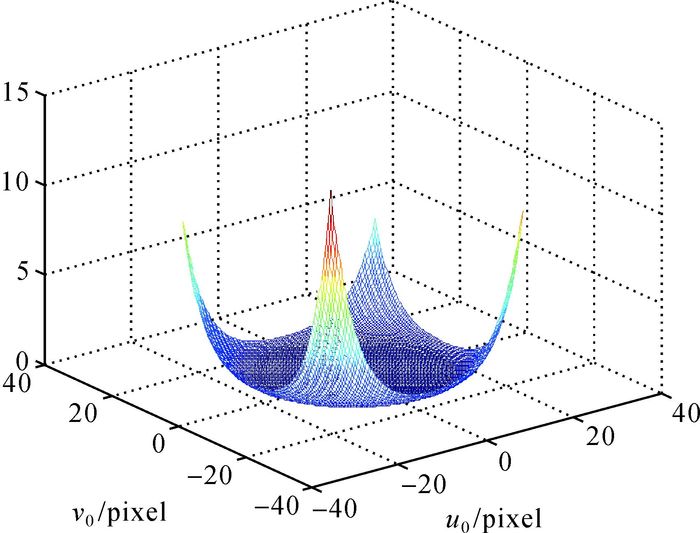
2.3 收敛性分析分析易知,g (k1, u0, v0)对参数k1为二次多项式函数,是凸函数形式,故通过最小二乘迭代求解可获得全局最优解;而g (k1, u0, v0)对于参数u0、v0为六次多项式函数,为非凸函数,故通过最小二乘迭代求解可能会获取局部最优解而非全局最优,因此像主点坐标(u0, v0)初值的选取对最终收敛结果尤为重要。由于主点坐标一般位于图像中心附近,故将图像中心坐标选为初值。图 2为选取的一张图像获取的函数g (k1, u0, v0)分别随u0、v0变化的趋势图。可以看出,图 2中由于主点坐标的取值范围在图像中心附近,故函数值只有一个极值点,说明把图像中心作为主点坐标初值进行迭代,可收敛至全局最优。
|
| 图 2 函数g随(u0, v0)变化的趋势图 |
(1) 读入两幅图像。
(2) 进行特征提取与匹配,本文采用SURF算子,用KNN+RANSAC算法匹配获取同名像点{xi, x′i}(i=1, 2, …, N)。
(3) 自适应选取同名像点{xp, x′p}(p=1, 2, …, n)(选取靠近图像中心位置范围内的同名点, 如初次可选取图像宽高的1/8范围,第二次选取1/4范围等),利用RANSAC鲁棒估计算法计算基本矩阵F。
(4) 参数初始化。自适应选取同名像点{xq, x′q}(q=1, 2, …, N-n)(选取远离图像中心位置范围内的同名点),由于获取的内点应满足基本矩阵约束(x′TFx=0),可以将畸变参数k1和主点坐标(u0, v0)作为待求参量建立误差模型,通过最小二乘参数平差求解改正量,校正畸变参数与主点坐标。
(5) 判断是否满足高斯-牛顿迭代收敛条件(迭代增量小于特定阈值ε1或达到迭代次数iter),若满足,则进入步骤(6);若不满足,则跳转步骤(4),直至满足收敛条件,算法转入步骤(6)。
(6) 判断是否满足全局收敛条件,d2=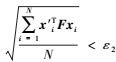
算法流程如图 3所示。
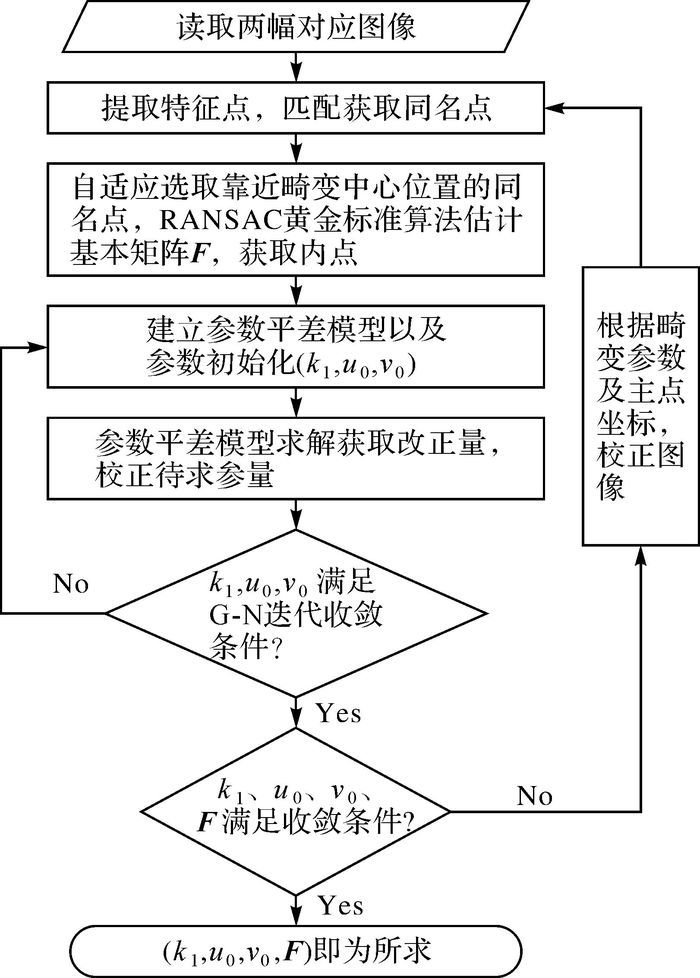
|
| 图 3 本文算法流程 |
为验证算法的有效性与正确性,设计了仿真试验和真实算例对算法性能进行分析。
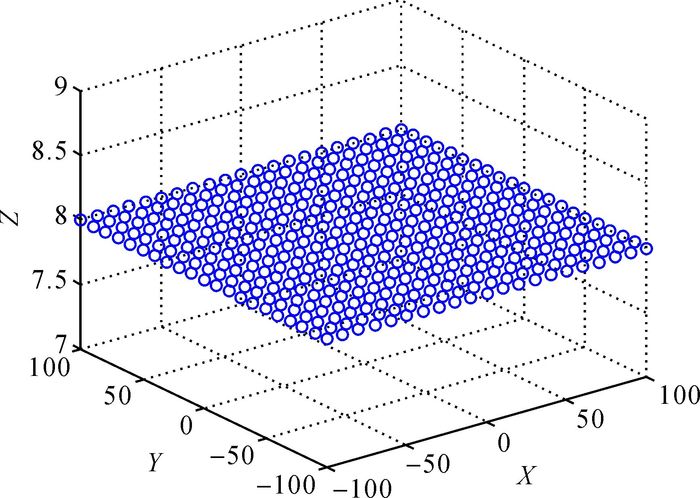
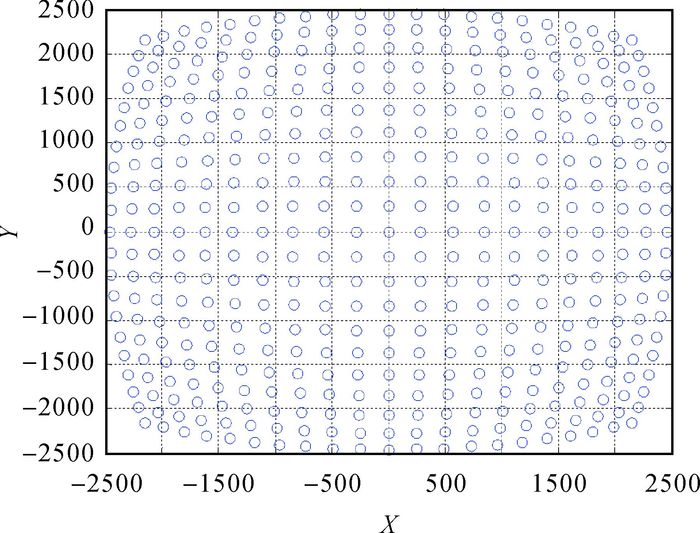
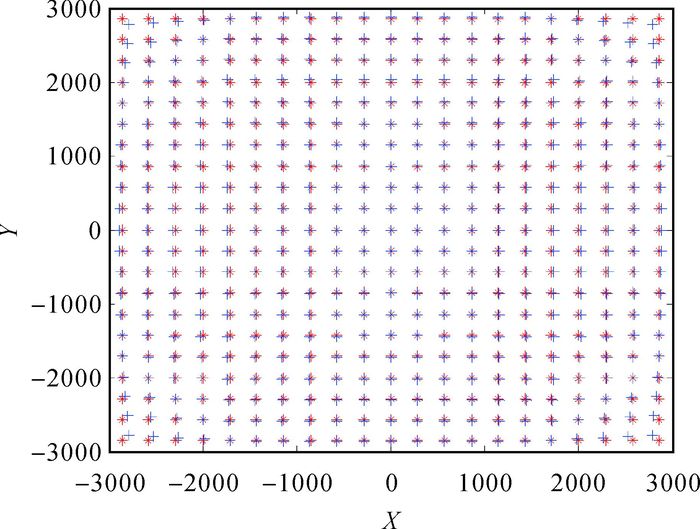
3.1 仿真试验因无法获取真实图像的真实像点坐标,故采用仿真试验来检验本文算法在不同量级噪声影响下的鲁棒性。首先生成21×21个三维空间点,令摄像机焦距为800像素,畸变参数k1=2×10-8,主点坐标为(0, 0),仿真生成两个摄像机外参矩阵[R1, T1], [R2, T2],根据摄像机成像模型得到两幅视图的真实像点坐标xu和x′u,利用畸变模型并加高斯噪声可得到仿真的对应像点坐标x和x′,图 4为仿真的三维点,图 5为针孔模型下的畸变图像,可看出图像有桶形畸变。利用本文算法处理得到畸变参数k1=-2.425 2×10-8,主点坐标为(0, 0),校正后的图像如图 6所示,其中*点为理想点,+点为纠正后像点。
|
| 图 4 仿真三维点 |
|
| 图 5 畸变图像 |
|
| 图 6 校正后图像 |
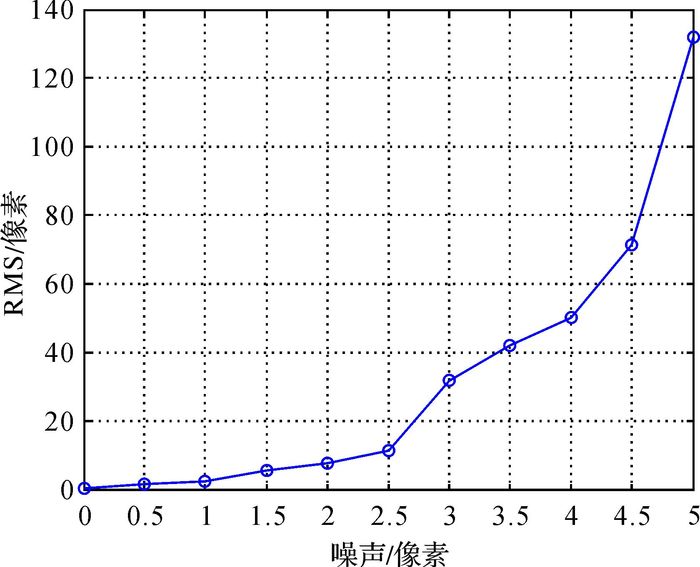
本文采用校正后像点坐标与对应真实像点坐标的均方根误差(RMS)作为评价指标,来衡量畸变校正效果的优劣。图 7为本文算法在不同噪声水平下的校正结果(畸变参数k1=-2×10-8)。噪声以0.5个像素为步长,每个噪声水平下的RMS值均为随机运行20次的平均值。由图 7可知,像点噪声将直接影响算法的性能,算法校正误差随噪声水平提高而增大。但目前的特征提取算法一般可将特征点定位至亚像素级,故本文算法仍具有较大的实用性。
|
| 图 7 算法校正结果与噪声水平的关系 |
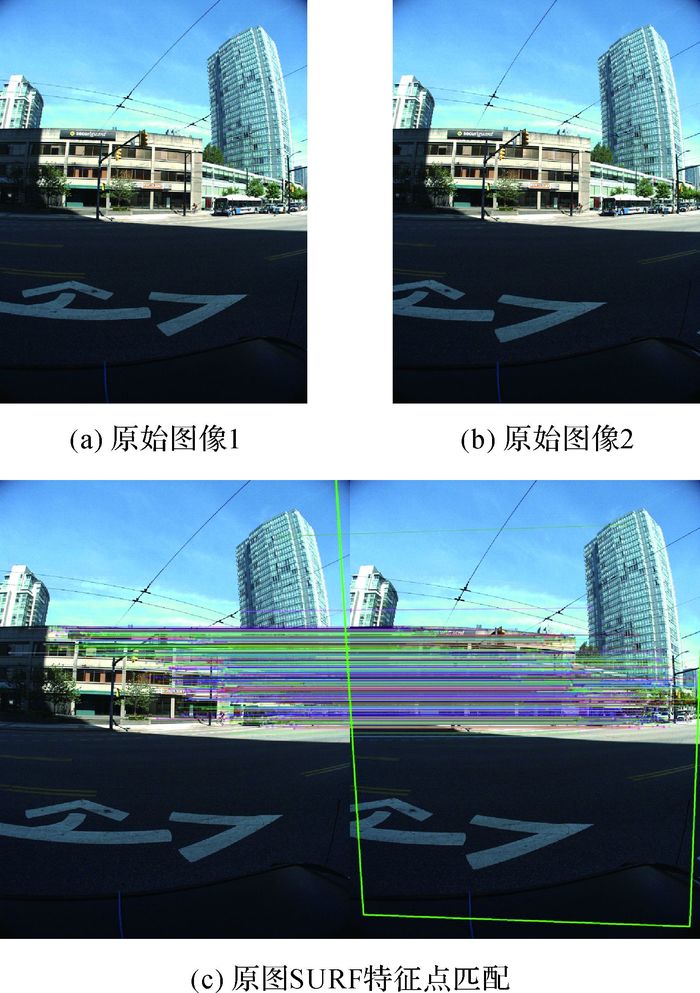
为验证算法的有效性,使用真实数据进行解算分析。使用Ladybug3全景视觉系统的SONY2.0 MP 1/1.8″ ICX274镜头采集连续两帧图像,图像大小为1232×1616像素,象元尺寸为4.4 μm,迭代计算初始值k1=0,主点坐标选为图像中心(616, 808),由于图像边缘部分畸变很大,基本矩阵F的初值采用靠近图像中心(|x-u0| < 150, |y-v0| < 200) 的匹配点进行计算,解算得到畸变校正前的F=

由8(a)和图 8(b)可看出,两幅原图都有较大的桶形畸变(k1为负值也说明了此问题),而畸变校正算法效果明显。校正后RANSAC匹配内点数由原来的820个变为956个,由图 8(c)和图 9(c)可看出,增加的内点数大都位于图像边缘附近,该区域也是畸变较大的区域。这是因为由畸变图像提取的同名点坐标(尤其是图像边缘的同名点坐标)不准确,导致一些本来符合内点条件的同名点也被剔除。为了证明解算结果的正确性,计算了校正前后所有同名点基础矩阵约束的残差D=∑i x′iTFxi/N,校正前为20.952 1(由于求解F时仅使用靠近图像中心的匹配点,故总体偏差较大),校正后为0.025 1。
|
| 图 8 原始图像及特征点匹配 |

|
| 图 9 校正后图像及特征点匹配 |
本文针对图像畸变问题,提出了一种图像自动校正的新方法。该方法基于对极几何的基本矩阵和一阶径向畸变模型构建两视图同名点约束方程;然后采用一种两步求解及分步迭代优化的分层策略优化基本矩阵并求解畸变参数和主点坐标。用RANSAC黄金标准算法估计两视图基本矩阵,用迭代最小二乘求解畸变系数和主点坐标,校正图像,两步求解交替进行,直至满足收敛条件。
(1) 本方法是一种独立的畸变校正算法,无需任何标定靶标,不受未知环境场景因素的影响,且避免了摄像机内参数之间的耦合影响,具有很强的适用性。
(2) 设计的分步求解策略避免了待求参数过多引起解不稳定的问题,使得算法实现具有稳健性。
(3) 本方法在进行畸变校正的同时,还获取了精确的图像主点坐标,有利于后续的摄像机自标定以及计算机视觉中的度量重建任务。
| [1] | 李晓明, 姚剑, 张继福. 摄像机畸变模型的比较与选择[J]. 计算机辅助设计与图形学学报, 2015, 27(5): 824–831. |
| [2] | TSAI R Y. A Versatile Camera Calibration Technique for High-accuracy 3D Machine Vision Metrology Using Off-the-shelf TV Cameras and Lenses[J]. Journal of Robotics & Automation IEEE, 1987, 3(4): 323–344. |
| [3] | ZHANG Z. A Flexible New Technique for Camera Calibration[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2000, 22(11): 1330–1334. |
| [4] | 叶峰, 王敏, 陈剑东, 等. 共面点的摄像机非线性畸变校正[J]. 光学精密工程, 2015, 23(10): 2962–2970. |
| [5] | MERRAS M, AKKAD N E, SAAIDI A, et al. Camera Self-calibration with Varying Parameters by an Unknown Three Dimensional Scene Using the Improved Genetic Algorithm[J]. 3d Research, 2015, 6(1): 1–14. DOI:10.1007/s13319-014-0034-3 |
| [6] | 洪洋, 孙秀霞, 蔡鸣, 等. 基于正交消隐点无穷单应的摄像机内参数自标定方法[J]. 中国激光, 2015(12): 182–192. |
| [7] | BRVCKNER M, BAJRAMOVIC F, DENZLER J. Intrinsic and Extrinsic Active Self-calibration of Multi-camera Systems[J]. Machine Vision & Applications, 2014, 25(2): 389–403. |
| [8] | 唐巍, 叶东, 袁锋, 等. 视觉测量系统中一种独立的畸变校正算法[J]. 光电子·激光, 2013(2): 308–315. |
| [9] | 薛俊鹏, 苏显渝. 基于两个正交一维物体的单幅图像相机标定[J]. 光学学报, 2012(1): 145–151. |
| [10] | 张敏, 金龙旭, 吴凡路, 等. 基于Hough变换的摄像机畸变非量测标定方法[J]. 光电子·激光, 2015(11): 2217–2223. |
| [11] | 陈天飞, 马孜, 李鹏, 等. 一种基于非量测畸变校正的摄像机标定方法[J]. 控制与决策, 2012, 27(2): 243–246. |
| [12] | 赵振庆, 叶东, 吴斌, 等. 消隐点共线约束逐点畸变校正算法[J]. 光学精密工程, 2015, 23(4): 1196–1204. |
| [13] | 周富强, 蔡斐华. 基于非量测畸变校正的摄像机标定方法[J]. 机械工程学报, 2009, 45(8): 228–232. |
| [14] | 张靖, 朱大勇, 张志勇. 摄像机镜头畸变的一种非量测校正方法[J]. 光学学报, 2008, 8(28): 1552–1557. |
| [15] | WENG J, COHEN P, HERNIOU M. Calibration of Stereo Cameras Using a Non-linear Distortion Model(CCD sensory)[C]//Proceedings of International Conference on Pattern Recognition.1990.[S.l.]:IEEE, 1990:246-253. |


