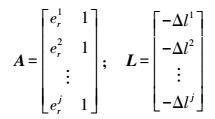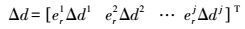2. 武汉大学测绘学院, 湖北 武汉 430079
2. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China
获取实时高精度的载体速度信息在无人机、GPS/INS组合导航及精细农业等领域具有重要作用[1-3]。相较于雷达测速、光波测速等,GPS接收机具有价格低廉、操作简单等优势,因而被广泛应用。随着美国SA政策的取消,GPS卫星轨道和卫星钟差精度大幅提高,使得利用单台GPS接收机确定运动载体的速度成为可能[4]。目前,利用GPS技术获取高精度运动载体速度的方法主要有3种:① 位置差分法,通过对连续的位置序列进行一次微分求解速度。该方法的缺陷在于对位置的精度要求较高,而实际测量中由于环境等因素的影响,模糊度参数往往难以固定,进而无法保证高精度的定位结果[5]。② 多普勒值法测速,又可分为原始多普勒值和基于相位观测值获得的导出多普勒值。原始度多普勒值观测噪声较大,精度一般不如导出多普勒观测值[6];而导出多普勒值,虽然精度较高,但其构造过程具有延迟性,无法用于高精度实时测速。③ 历元间差分法(TDCP),通过相邻历元相位观测值求差,可消除常数偏差项并降低时域相关的大气误差的影响,进而获得高精度的位移变化量[7]。一般情况下,用于监测载体动态信息的数据采样率较高(≥1 Hz),因而可将此位移信息转化为载体的瞬时速度。
TDCP方法对历元间误差的变化量十分敏感,一般认为短时间内大气误差、卫星轨道及卫星钟差都十分稳定。在排除周跳影响的情况下,采用广播星历即可获得毫米级精度的位移变化量。对于单点定位等大多数逐历元算法而言,当前观测信息只涉及单个历元,因此在广播星历选择上采用就近原则是可行的[8]。然而,TDCP方法涉及两个历元的观测信息,星历更新会导致卫星轨道和钟差的跳变,使得节点处的速度估值出现偏差,因而传统就近选择星历的方法将不再适用。
针对上述存在的问题,本文将首先介绍TDCP法的基本原理,然后详细分析广播星历更新时卫星轨道和钟差跳变对TDCP法估计速度参数的影响,并提出改进的策略,最后评估实时单频测速的精度。
1 TDCP基本原理TDCP由Van Grass等[4]提出,利用历元间相位观测值求差可实时获取单站载体速度。相位观测方程可简写如下
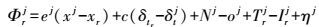 (1)
(1) 式中,Φrj为相位观测值,单位为m;erj为站星间方向余弦; xj和xr分别为卫星和载体的三维坐标; c为真空环境下的光速; δtr和δtj为载体和卫星端钟差; Nj为模糊度参数;ξj为误差项;oj为星历误差(卫星轨道误差和钟差误差);Irj为电离层延迟;Trj为对流层延迟;ηj为观测噪声。
对式(1) 历元间求差,并令xr(tk)=xr(tk-1)+Δx,Δx为历元tk-1至tk载体的位移变化量,于是可得
 (2)
(2) 式中,Δ为历元间差分算子。当相位观测值连续时,模糊度参数Nj可通过历元间差分消除,电离层延迟ΔI j可采用无电离层组合消除一阶项误差;短时间内(≤1 s),对流层延迟ΔT j变化非常小,可忽略不计;卫星轨道和卫星钟差认为短时内非常平稳,因此Δoj一般也不予考虑[9-10];卫星轨道、卫星钟差及接收机位置均可由广播星历实时计算获得。将式(2) 整合可得
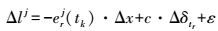 (3)
(3) 式中
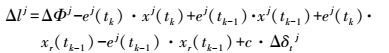 (4)
(4) 式中,左边为已知项;右边仅剩待估参数X=[Δxc·Δδt]T和误差项ε。采用高度角定权的方式确定权阵P[11],则式(3) 可矩阵表达为
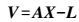 (5)
(5) 式中
采用抗差最小二乘可解算待估参数[12]
 (6)
(6) 最终将所得位移变化量Δx除以数据采样时间间隔,便可获得载体速度。
由于广播星历每2 h更新一次,星历更新使得卫星轨道和卫星钟差不再连续。假设卫星钟差跳变大小为Δt,则由式(3) -式(6) 可得卫星钟差对参数估计的影响为
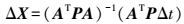 (7)
(7) 卫星轨道影响主要由该项-ej (tk)·xj (tk)+ej (tk-1)·xj (tk-1)决定。短时内方向余弦基本一致,即erj(tk)≈erj(tk-1),则轨道误差的影响可表示为
 (8)
(8) 式中,Δxj为同一星历数据块计算的轨道误差;Δdj为星历更新导致卫星轨道跳变的大小。当相邻历元采用同一星历基准时,轨道误差Δxj一般在毫米量级,因此可以忽略不计;当相邻历元星历基准不一致时,则轨道跳变对参数估计的影响可表达为
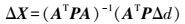 (9)
(9) 式中
2 TDCP数据处理本文除分析广播星历更新对TDCP方法的影响外,还将评估实时单频单站测速的精度。由于载体速度真值较难获取,选用静态模拟动态的方式评估精度。采用U-blox单频接收机实时采集GPS数据,时间为2016年12月22日12:22:45-23:59:59(UTC),数据采样间隔为1 s,数据采集地点为GFZ实验楼顶,视野开阔无遮挡。
2.1 星历数据块更新影响分析选取可视时间较长的4颗卫星G13、G15、G24、G30,分别分析星历数据块更新造成的轨道和钟差跳变大小。
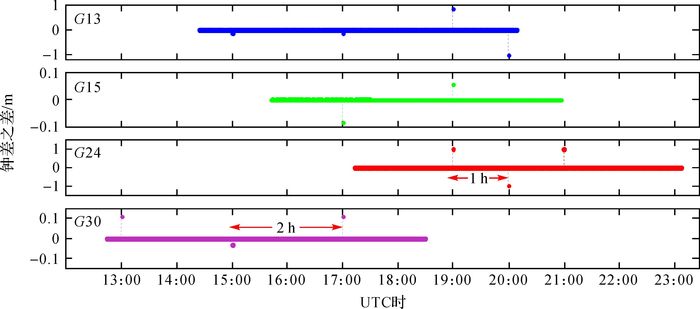
对卫星钟差求历元间差,结果如图 1所示。横坐标为UTC时,纵坐标为历元间钟差之差。图中相邻突变点间隔较大的为2 h,间隔较小的为1 h。当采用同一星历数据块解算卫星钟差时,历元间钟差变化量几乎为0,可以忽略不计;而当星历数据块更新时,会造成不同程度的卫星钟差跳变。图中钟差跳变最小约为0.03 m,最大可达1.01 m。以G30为例,星历在14:00:00和16:00:00更新。采用传统就近原则,当信号播发时刻处于14:00:00-15:00:00时,选择14:00:00时刻的星历数据块,而当信号播发时刻处于15:00:00-16:00:00时,则选择16:00:00时刻的星历数据块。这就导致若相邻观测历元正好位于15:00:00两边时,两者所选用的星历数据块不一致,从而发生数据跳变。此外,一般情况下广播星历数据块每2 h更新一次(图中G15、G30),由于卫星与地面控制站固件问题会造成非整点时刻更新数据块[13](图中G13、G24),且非整点时刻数据块约占所有数据块的17%左右,这使得卫星钟差间断较为频繁。如G24,除了每2 h在整点更新星历外,还分别在19:59:44和21:59:44(UTC)更新了星历。
|
| 图 1 星历数据块更新对卫星钟差的影响 |
由于卫星轨道跳变量相较于轨道变化非常小,此处仅统计星历更新节点处的轨道跳变量。分别采用相邻星历数据块计算节点时刻的卫星轨道,并用式(10) 求两者的3D位置差,结果见表 1。
| m | ||||
| UTC时 | G13 | G15 | G24 | G30 |
| 13:00:01 | 0.02 | - | - | 0.09 |
| 15:00:01 | 0.32 | - | - | 0.15 |
| 17:00:01 | 0.30 | 0.37 | - | 0.15 |
| 18:59:54 | 0.51 | 0.51 | 2.02 | - |
| 19:00:01 | - | - | - | - |
| 19:59:54 | 0.09 | - | 1.71 | - |
| 21:00:01 | - | 0.22 | 1.75 | - |
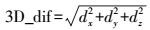 (10)
(10) 式中,dx、dy、dz分别为卫星轨道在WGS-84坐标系下的位置差。
与卫星钟差跳变情况类似,不同卫星及同一卫星不同时间节点跳变的大小均不相同。本算例中,轨道跳变最小为0.02 m,最大为2.02 m,多数处于分米级变化量。由式(7) 和式(9) 可知,卫星钟差和轨道跳变会对参数估计造成很大影响。
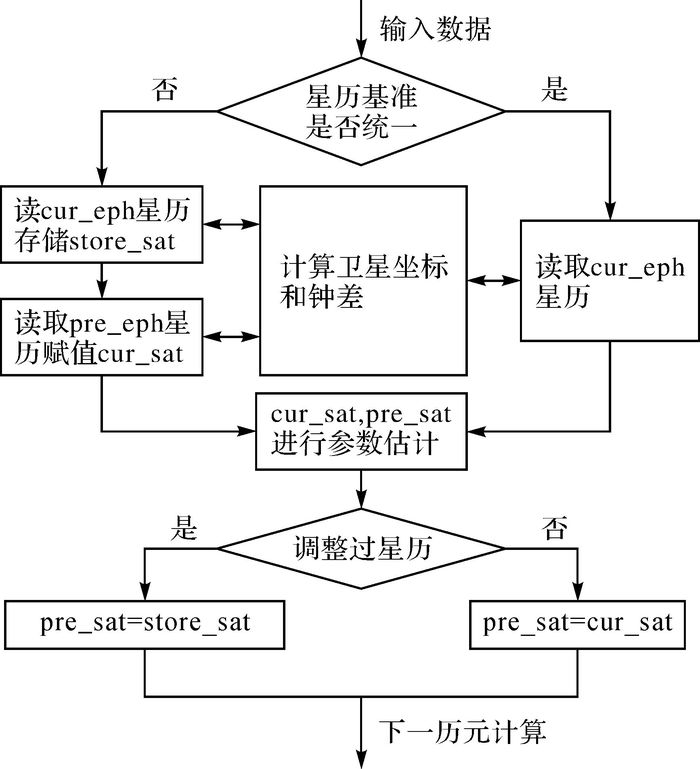
2.2 数据处理流程由以上分析可知,传统就近原则选择星历基准的策略不再适用于TDCP方法,因此本文对数据处理方法进行了改进,数据流程如图 2所示。① 判断当前历元是否与前一历元星历数据块一致。② 若不同,则利用当前星历数据块cur_eph计算卫星坐标和钟差,并保存至store_sat,同时读取前一星历数据块pre_eph,并将计算的卫星坐标和钟差信息赋值给cur_sat;若相同,则读取cur_eph,并计算卫星坐标和钟差。③ 利用当前历元卫星信息和上一历元卫星信息采用最小二乘估计参数。④ 判断是否调整过星历基准,若是,则将store_sat赋值给pre_sat;若否,则将cur_sat赋值给pre_sat,并进行下一历元数据处理。
|
| 图 2 数据处理流程 |
为分析卫星轨道和钟差跳变对测速的影响,设计了3种试验方案,见表 2。方案1:星历更新时刻卫星轨道采用同一星历数据块计算,而卫星钟差采用不同星历数据块计算;方案2,卫星轨道采用不同星历数据块计算,卫星钟差采用相同数据块计算;方案3,全部采用同一星历数据块计算。
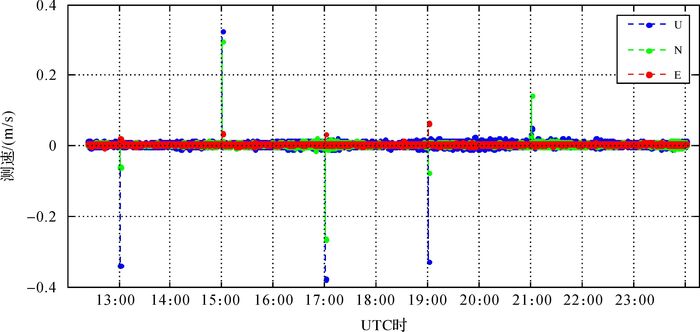
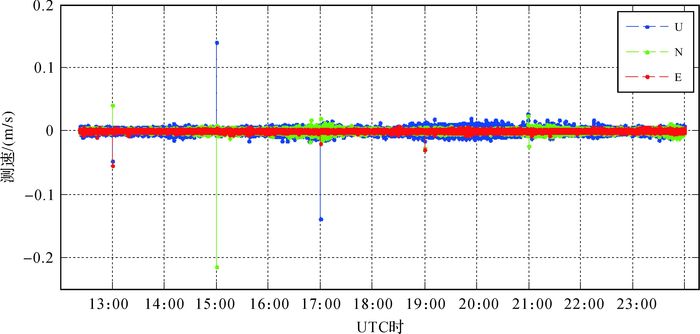
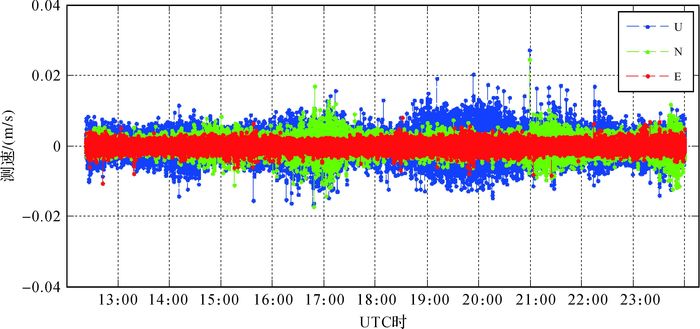
3种方案计算的载体实时速度如图 3-图 5所示。由于测站静止,速度真值认为是0。将速度估值与0求差,并将差值转到当地水平坐标系,其中黑色、白色和灰色点线分别代表U、N、E 3个方向的速度偏差。由图 3、图 4可知,卫星钟差和轨道跳变对速度的影响可达分米级,其中卫星钟差的影响较卫星轨道的影响要大,如在19:00:01和21:00:01处卫星轨道跳变对参数估计影响几乎可以忽略。其原因可能是相对于卫星钟的变化卫星轨道比较稳定,当星历数据更新时,部分卫星轨道模型变化并不是很大,由此引起的跳变量相对较小。图 5为采用本文数据处理策略计算得到的速度结果,可见星历数据块更新并不会影响参数估计结果。对方案3的结果进行统计,得到3方向速度偏差均值为0 mm/s,U方向均方根误差为3.0 mm/s,N方向均方根误差为2.8 mm/s,E方向均方根误差为1.1 mm/s,满足高精度实时测速的要求。
|
| 图 3 方案1单站实时测速结果 |
|
| 图 4 方案2单站实时测速结果 |
|
| 图 5 方案3单站实时测速结果 |
采用传统就近原则选择广播星历数据块,会使得相邻历元所采用的星历不一致,从而出现卫星轨道和钟差跳变的现象。本文首先分析了由于星历数据块更新导致的卫星轨道和钟差跳变对TDCP实时测速的影响。结果表明,星历更新会造成卫星轨道和钟差厘米级到米级的跳变,且不同卫星或同一卫星不同时刻跳变量并不相同。卫星钟差跳变较卫星轨道跳变而言,对参数估计的影响略高。
采用改进的数据处理方法,可有效避免这一问题。笔者处理了约12 h的静态单频实时数据。结果表明,利用TDCP方法获得的载体速度,在U、N、E 3个方向的速度偏差为0 mm/s,均方根误差在1~3 mm/s左右,满足高精度测速要求。
| [1] | 张小红, 郭博峰. 单站GPS测速在实时地震监测中的应用[J]. 地球物理学报, 2013, 56(6): 1928–1936. DOI:10.6038/cjg20130615 |
| [2] | SERRANO L, KIM D, LANGLEY R B, et al.A GPS Velocity Sensor:How Accurate can It Be?-A First Look[C]//Proceedings of the National Technical Meeting of the Institute of Navigation.[S.l.]:[s.n.], 2004:875-885. |
| [3] | DING W, WANG J. Precise Velocity Estimation with a Stand-alone GPS Receiver[J]. Journal of Navigation, 2011, 64(2): 311–325. DOI:10.1017/S0373463310000482 |
| [4] | ZHANG J, ZHANG K, GRENFELL R, et al. On Real-time High Precision Velocity Determination for Standalone GPS Users[J]. Survey Review, 2013, 40(310): 366–378. |
| [5] | 郑凯, 刘站科, 肖学年, 等. 航空重力GPS测速多粗差探测方法[J]. 测绘学报, 2016, 45(6): 663–669. DOI:10.11947/j.AGCS.2016.20150481 |
| [6] | SERRANO L, KIM D, LANGLEY R B.A Single GPS Receiver as a Real-time, Accurate Velocity and Acceleration Sensor[C]//Proceedings of the 17th International Technical Meeting of the Satellite Division of The Institute of Navigation.[S.l.]:[s.n.], 2004:21-24. |
| [7] | GRAAS F V, SOLOVIEV A. Precise Velocity Estimation Using a Stand-alone GPS Receiver[J]. Navigation, 2004, 51(4): 283–292. DOI:10.1002/navi.2004.51.issue-4 |
| [8] | 向涛, 史俊波, 郭际明. GPS广播星历非整点时刻数据块对伪距单点定位的影响研究[R]. 南京: 中国卫星导航学术年会, 2014. |
| [9] | ZHENG K, TANG L. Performance Assessment of BDS and GPS/BDS Velocity Estimation with Stand-alone Receiver[J]. Journal of Navigation, 2016, 69(4): 869–882. DOI:10.1017/S0373463315000958 |
| [10] | 王甫红, 张小红, 黄劲松. GPS单点测速的误差分析及精度评价[J]. 武汉大学学报(信息科学版), 2007, 11(6): 515–519. |
| [11] | KING R W, BOCK Y. Documentation for the GAMIT GPS Analysis Software, Release 10.2'[J]. Iw Igs 1997 Technical Reports, 2009(5): 37–41. |
| [12] | 杨元喜. 等价权原理──参数平差模型的抗差最小二乘解[J]. 测绘通报, 1994(6): 33–35. |
| [13] | LIANG H, GAO G X, WALTER T, et al.GPS Ephemeris Error Screening and Results for 2006—2009[C]//Proceedings of the 2010 International Technical Meeting of The Institute of Navigation.[S.L.]:[s.n.], 2010. |