2. 中国科学院空间信息处理与应用系统技术院重点实验室, 北京 100190;
3. 中国科学院大学, 北京 100049;
4. 中国国际工程咨询公司, 北京 100048
2. Key Laboratory of Spatial Information Processing and Application System Technology, Chinese Academy of Sciences, Beijing 100190, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China;
4. China International Engineering Consulting Corporation, Beijing 100048, China
干涉合成孔径雷达技术(interferometric synthetic aperture radar, InSAR)是一种可以获取高分辨率地形轮廓,测量雷达目标沿雷达视线方向形变的微波遥感技术,它是合成孔径雷达遥感成像与电磁波干涉两大技术融合的结果。主要分为3个发展阶段:差分干涉SAR技术,时序干涉SAR技术,第二代时序干涉SAR技术。
差分干涉技术(differential interferometric synthetic aperture radar,DInSAR)[1]利用在地表同一地区不同时间获取的两幅SAR影像的差分相位信息获取地表形变信息,与传统的监测手段相比,具有全天时、全天候、高分辨率、广覆盖、低成本等优势。然而受制于时间和空间去相干及不同时刻大气波动的影响,利用DInSAR技术进行长时间的地表微小形变监测时,精度受到很大限制,而且对辅助DEM的精度要求也非常高,很难达到理想的米级DEM和毫米级形变监测能力。为了克服这些限制,研究人员提出了以下几种多时相干涉SAR技术,如永久散射体干涉合成孔径雷达技术(persisitent-scatterer InSAR,PSI)[1-5]、差分层析SAR技术(differential SAR tomography)[6], 以及最小基线集技术(small baseline subset InSAR,SBAS-InSAR)[7-9],通过处理稳定点目标上的相位信息,最大限度地克服了去相干因素及大气干扰的影响,实现了高精度地表形变的反演。
然而,以上几种多时相干涉SAR技术都存在同一种缺陷,在影像中高相干性像素点分布并不均匀,表现为在城区和岩石裸露的地区密度高,而在非城区等低相干地区密度较低。因此为了增加非城区等低相干地区形变监测点的密度,Ferretti等在2011年提出了第二代多时相干涉SAR技术(SqueeSAR技术[10]),通过空域自适应滤波和极大似然方法从永久散射点(PS)和分布散射点(distributed scatterers,DS)中提取形变信息。然而该技术只能对单像素处理,对配准精度要求较高,而利用一种新的第二代时序干涉SAR技术,联合像素干涉SAR处理技术[11](joint scatterer InSAR, JSInSAR)能够有效克服上述缺点,该技术利用邻近像素的相干信息,即使在较大的配准误差下依然能有效地提高分布式散射点的信噪比,提高低相干区域监测点的空间密度,同时获取高相干和低相干区域的形变信息。本文对联合像素时间序列干涉SAR技术进行分析,首先建立信号模型,应用拟合优度检验方法和空域自适应滤波方法获取优化相位,同时提出基于KSTEST统计检验[4, 12]思想的联合像素拟合优度检验方法,并对该方法重点阐述,包括其数学模型、处理流程和试验结果。
1 联合像素时间序列干涉SAR技术 1.1 信号模型给定N景已配准的单视复数据SAR影像,联合数据向量ux表示为
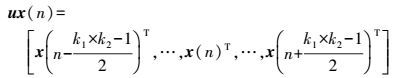 (1)
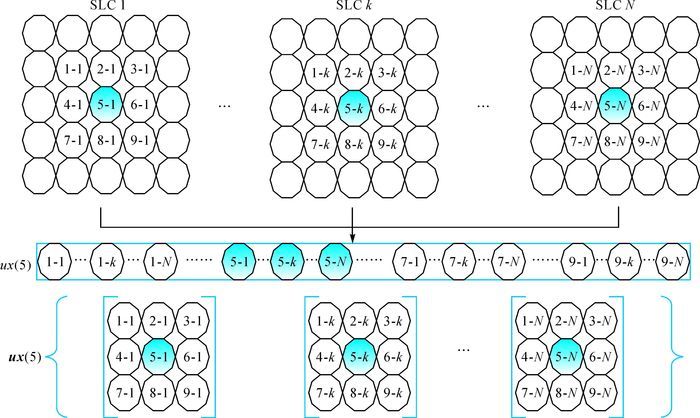
(1) 式中,T为向量转置;k1和k2为窗口尺寸,假设为奇数;x (i)为单像素向量,x (i)=[x1(i), …, xN(i)],其中,i∈[n-(k1×k2-1) /2, n+(k1×k2-1) /2];对应地面同一分辨率单元,x (n)表示将被滤波处理的像元,其N个元素代表该像元在N幅影像中的相位值,滤波处理后N个像元相位值被更新,信噪比提升。信号模型直观解释如图 1所示,中央5号像元表示被处理像元。
|
| 图 1 在3×3窗口下的联合散射体向量 |
令k′=(k1×k2-1) /2,联合像素向量ux (n)可以用下式表示
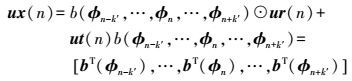 (2)
(2) 式中,⊙表示Hadamard积;bT(φn-k′)=…=bT(φn)=…=bT(φn+k′)=exp(jφn)φn=[v1, v2, …, vN],表示待估计的干涉相位;ur (n)表示复数回波向量;ut (n)表示加性噪声,假定为空间相互独立的复高斯白噪声,均值为零,方差为σuw2。
在式(1) 中,联合复数据向量在基于中心极限定理的高斯散射假设下,可以模型化为联合零均值复圆高斯随机向量。
令ub (φn)=b (φn-k′, …, φn, …, φn+k′),对应的协方差矩阵为
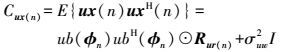 (3)
(3) 式中,H表示向量的共轭转置;Rur (n)为仅包含信号分量的相关系数矩阵。
上述联合像素信号模型不能用传统的假设检验方法,因此针对该模型,提出了新的基于KSTEST统计检验方法的拟合优度检验方法。
1.2 拟合优度检验拟合优度检验是一种常用统计检验方法,通过计算检验统计量,并与临界值进行比较来检验样本序列分布是否与某假设理论分布相一致,它是空域自适应滤波算法不可缺少的步骤,通过它即可确定哪些像素被用于滤波。
传统拟合优度检验方法只适用于一维向量,不能直接应用于多维联合像素统计同分布拟合优度检验。传统的联合像素拟合优度检验使用参数化极大似然比检验法,必须首先知道散射点统计特性,而由于多数地物统计特性比较复杂,难以应用先验知识获取地物的统计分布函数,因此笔者提出一种基于双样本KSTEST统计检验思想的联合像素拟合优度检验方法,该方法不需要知道散射点统计特性的先验知识,可以很好地克服传统的参数化联合像素拟合优度检验的缺点,主要分为两个步骤:
(1) 在空间维(一景SAR影像中),运用KSTEST检验法求取两个联合像素数据块最大块离散度(maximum patch dissimilarity),将其定义为两个数据块的相似度。
(2) 在时间维,将所有影像中最大块离散度的最大值作为两个联合像素向量的相似度,定义为时序拟合优度检验统计量,当该统计量小于给定阈值时,两个联合数据向量是统计同分布的,两个联合像素向量假设检验可定义如下:
H0:联合像素向量ux1和ux2统计同分布
H1:联合像素向量ux1和ux2不是统计同分布
首先,定义两个联合像素数据块x1, k和x2, k,其中像素数目均为M=k1×k2,按照幅值将像元由小到大排序,积分分布函数的无偏估计SM (x)定义如下
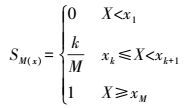 (4)
(4) 式中,xk为数据块幅值中第k个值。
第j幅单视复图像中最大块离散度(maximum patch dissimilarity)可以有如下定义
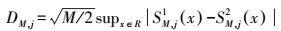 (5)
(5) 式中,j=1, 2, …, N。DM, j值越小,相似度越高,积分分布函数Y(t)定义如下
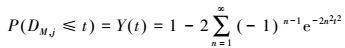 (6)
(6) 上述积分分布函数不依赖于具体的概率分布函数,因此上述方法称为非参数检验方法,当DM, j≤c时认为两个数据块x1, k和x2, k是统计同分布的,阈值c依赖于给定的置信度水平α=1-Y(t),时序拟合优度检验统计量有如下定义
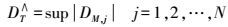 (7)
(7) 当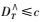
本方法具有良好的稳健性和对尺度变化不敏感等优点,在实测数据中取得了较好的效果,相比于SqueeSAR技术和PSI技术,提升了监测点的空间密度和信噪比,与传统的基于经验似然比的拟合优度检验方法相比,效率更高。
1.3 空域自适应滤波空域自适应滤波广泛应用于图像去噪中。在SAR处理中,更多用于斑点噪声去除和干涉图滤波,以及协方差矩阵估计。由于缺少恰当的统计检验方法且只针对一维向量,绝大多数现有的空域自适应滤波算法不能直接应用于时序干涉SAR处理。联合像素空域自适应滤波是对联合数据向量进行滤波,针对多维像素,因此必须应用上节提出的统计同分布检验方法定义滤波权重,并获取协方差矩阵。
同分布联合数据向量ux (l)的权重为ε(l)=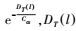
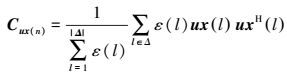 (8)
(8) 式中,Δ为同分布联合数据向量的集合。通过对矩阵特征分解,获得优化后的干涉相位。
2 试验与分析本文利用某机场区域32景TerraSAR-X Stripmap数据,拍摄时间为2012-01-22—2016-03-08。应用本文提出的基于KSTEST统计检验方法的JSInSAR技术作出了该机场草坪区域形变结果,并与PSI技术、SqueeSAR技术及传统的基于经验似然比拟合优度检验方法的JSInSAR技术结果进行了对比。
对比结果如图 2所示,图中处理区域由方框标注,从图中可以看出,方框以外的区域,监测点空间密度分布并不均匀,在建筑物等高相干区域,监测点的空间密度较高,在机场草坪区域等低相干地区,监测点空间密度较低,甚至没有;在方框内部,PSI技术基本没有获取有效监测点,说明该区域散射点信噪比并没有得到有效提升,因此无法获取草坪区域形变信息。SqueeSAR有少部分监测点,说明该区域散射点信噪比和相干性得到部分提升,但由于监测点的空间密度依然较低,依然无法有效获取草坪区域形变信息;相比于上述两种技术,基于极大似然比的参数化联合像素方法(JSInSAR-ML),监测点空间密度得有效提升,说明大部分监测点的信噪比和相干性得到较好提升,但草坪中间区域没有获取有效监测点,说明该区域去相干较严重,散射点的信噪比和相干性提升并不明显,而本文提出的基于KSTEST方法的非参数拟合优度检验方法可以有效增加全部草坪区域监测点空间密度,即使在信噪比和相干性均较低草坪中间区域,依然能够有效提升散射点的信噪比和相干性,因此该方法获取的形变信息更加完整全面,可以看出本文方法相比于传统方法有明显优势,极大提升了多时相干涉SAR技术形变监测的能力。

|
| 图 2 ${paragraph.title} |
联合像素干涉SAR技术能够有效提升相干性较低区域的信噪比,提升形变监测点的空间密度,关键技术流程为:联合像素模型建立,拟合优度检验方法,空域自适应滤波。本文提出的基于KSTEST统计检验思想的联合像素拟合优度检验方法,在实际数据中相比于传统的PSI技术、SqueeSAR技术,以及基于最大似然比的JSInSAR技术,有效提升了机场草坪区域分布式散射点的空间密度,极大提升了干涉SAR技术的形变监测能力。
| [1] | FERRETTI A, PRATI C, ROCCA F. Permanent Scatters in SAR Interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(1): 8–20. DOI:10.1109/36.898661 |
| [2] | FERRETTI A, PRATI C, ROCCA F. Nonlinear Subsidence Rate Estimation Using the Permanent Scatterers in Differential SAR Interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(5): 2202–2212. DOI:10.1109/36.868878 |
| [3] | 刘国祥, 陈强, 罗小军, 等. 永久散射体雷达干涉理论与方法[M]. 北京: 科学出版社, 2012. |
| [4] | 孙倩, 朱建军, 李志伟, 等. 基于信噪比的InSAR干涉图自适应滤波[J]. 测绘学报, 2009, 38(5): 422–437. |
| [5] | 秦晓琼, 杨梦诗, 王寒梅, 等. 高分辨率PS-InSAR在轨道交通形变特征探测中的应用[J]. 测绘学报, 2016, 45(6): 713–721. DOI:10.11947/j.AGCS.2016.20150440 |
| [6] | FORNARO G, REALE D, SERAFINO F. Four Dimensional SAR Imaging for Height Estimation and Monitoring of Single and Double Scatterers[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(1): 224–237. DOI:10.1109/TGRS.2008.2000837 |
| [7] | BERARDINO P, FORNARO G, LANARI R, et al. A New Algorithm for Surface Deformation Monitoring Based on Small Baseline Differential SAR Interferograms[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(11): 2375–2383. DOI:10.1109/TGRS.2002.803792 |
| [8] | 梁涛. 利用短基线集InSAR技术监测矿区地表形变[J]. 测绘通报, 2014(S2): 82–84. |
| [9] | 谢荣安, 周元华, 胡争. 短基线集技术在地表形变监测中的应用研究[J]. 测绘通报, 2015(8): 70–73. |
| [10] | FERRETTI A, FUMAGALLI A, NOVALI F, et al. A New Algorithm for Processing Interferometric Data-Stacks:SqueeSAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(9): 3460–3470. DOI:10.1109/TGRS.2011.2124465 |
| [11] | LV X, YAZICI B, ZEGHAL M, et al. Joint-Scatterer Processing for Time-Series InSAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(11): 7205–7219. DOI:10.1109/TGRS.2014.2309346 |
| [12] | 朱益稼, 于凤芹, 陈莹. 基于拟合优度检验的图像序列变化检测[J]. 计算机工程, 2015, 41(12): 226–230. DOI:10.3969/j.issn.1000-3428.2015.12.043 |
| [13] | 兰冲锋. 统计学教学中关于假设检验问题探讨[J]. 湖南城市学院学报(自然科学版), 2016, 25(2): 303–304. |
| [14] | 王彦兵, 洪伟, 李小娟, 等. 基于D-InSAR技术的北京城区地面沉降监测[J]. 测绘通报, 2016(5): 66–68. |
| [15] | ROSEN P A, HENSLEY S, JOUGHIN I R, et al. Synthetic Aperture Radar Interferometry[J]. Proceedings of the IEEE, 2000, 88(3): 333–382. DOI:10.1109/5.838084 |


