2. 北京超图软件股份有限公司, 北京 100015;
3. 北京市地理信息核心软件与应用工程技术研究中心, 北京 100015
2. SuperMap Software Co., Ltd., Beijing 100015, China;
3. Beijing Research Center of Geography Information Core Software and Applied Engineering Technology, Beijing 100015, China
邻近图分析始于20世纪80年代。近年来,随着对邻近图研究的深入[1],基于邻近图理论的相关研究在地理空间分析中得到应用。郭庆胜等验证了基于邻近图的点集聚类分析的可行性,并使用不同的邻近图分析得到不同的聚类效果[2];宋晓梅等通过k阶空间邻近图处理空间聚类问题[3];Adamatzky等使用邻近图进行道路演化分析[4],并使用微观模拟得到较好的研究结果。道路网络是道路网络分析的空间地理对象[5-7],道路网络特征分析在道路网络演化分析中具有重要作用[8-9]。邻近性特征分析是进行道路网络结构分析、道路网络数据模拟、道路网络演化等空间网络分析采用的基础方法,本文采用基于邻近图理论的方法分析北京道路网络的邻近图特征。
1 邻近图理论简介考虑到邻近图的相关性质与道路网络特征,本节选取6种邻近图类型进行分析。
(1) 近邻邻近图(nearest neighbor graph,NNG):平面点集中每个点与最近的若干个点连接形成结果图。
(2) 最小生成树(minimum spanning tree,MST):平面点集之间的生成树,要求满足边集合的长度总和最小。
(3) 相关邻近图(relative neighborhood graph,RNG):即若∀u, v∈V,边(u, v)∈RNG;若不存在点w,则max{d(u, w), d(v, w)}<d(u, v)。
(4) Gabriel图(gabriel graph, GG):若∀u, v∈V,边(u, v)∈GG;若不存在点w,则max{d2(u, w), d2(v, w)}<d2(u, v)。
(5) 德罗内三角网(delaunay triangulation, DT):平面点集生成邻接不重叠的三角形,每个三角形的外接圆中不包含点集中任何其他点。
(6) Urquhart图(urquhart graph, UG);平面节集的DT图中去掉每个三角网中长度最长的那条边之后所生成的图。
由上述描述和性质可知,基于平面点集的邻近图满足如下关系
NNG⊆MST⊆RNG⊆GG⊆UG⊆DT
Beta骨架图(beta-skeleton graph,BG)也是一种常见的邻近图,由于BG的参数灵活[10-11],OSaragi等将其应用到道路网络分析中[12]。Beta骨架图中,当β=0时,BG图为DT;当β=1时,BG图为GG;当β=2时BG图对应为RNG。
为了更好地理解邻近图,图 1为基于相同100个网络节点的6种类型邻近图的示意图。
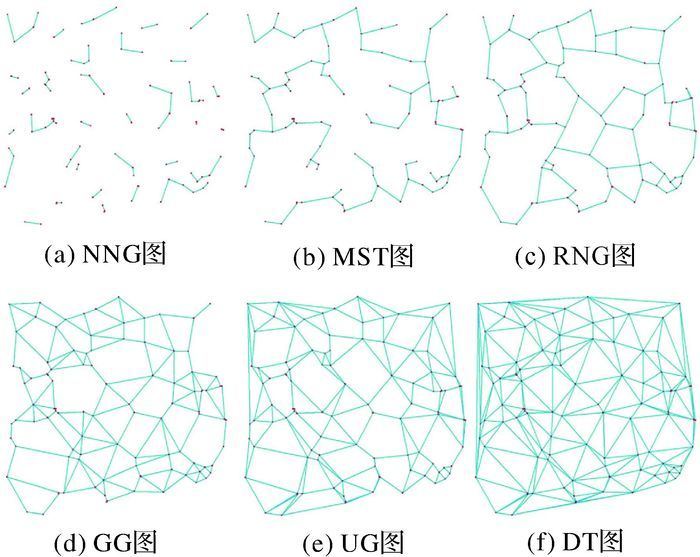
|
| 图 1 100个随机点生成的6种邻近图 |
在邻近图构建过程中,需要运行多次邻近点查询,邻近点查询的效率直接影响邻近图分析的效率,特别是网络节点GG和DT图的构建计算中,邻近点查询次数最多。为了提高道路网络节点的邻近点查询效率,针对道路网络节点数据较大的情况,采用基于空间索引[13-14](KD-Tree索引)的方法进行邻近节点查询,从而提高基于道路网络节点集的邻近图的构建效率。
研究数据选取北京六环内道路网络数据,其道路网络的网络弧段为双向道路,而基于网络节点的邻近图的弧段是由直线组成的,需要对道路网络进行拓扑处理。采用基于KD-Tree索引的邻近图计算后,得到6种邻近图的计算结果,如图 2所示。
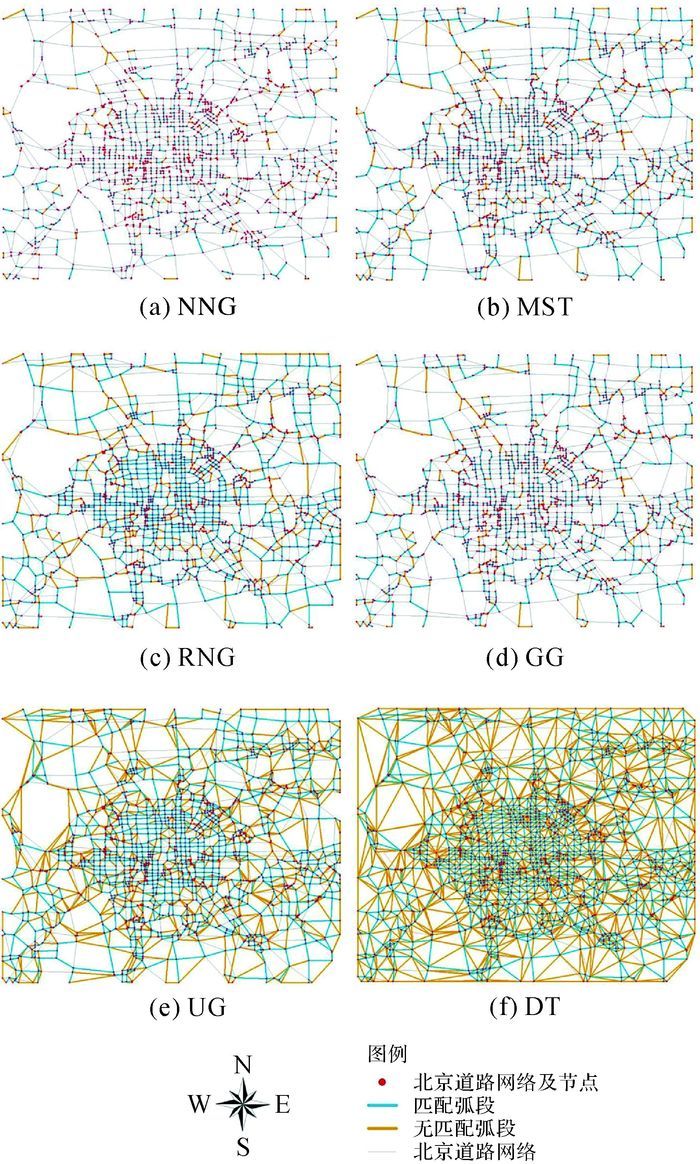
|
| 图 2 基于北京道路网络节点的邻近图与道路网络匹配图 |
为了评估道路网络与其对应的网络邻近图的关系,本节结合道路网络构成比率指数(包括道路网络构成比率、邻近图构成比率、全局构成比率)、格网树指数和网络节点因子等分析其道路网络节点生成的邻近图特征。
(1) 道路网络构成比率(road graph edge ratio, RR)反映的是道路网络节点生成的邻近图与道路网络的弧段匹配绝对程度,其数值为道路网络节点生成的邻近图与道路网络中相同的弧段数,与道路网络中的弧段个数的比值。不同邻近图中与道路网络中相同的弧段数越多,该比率越大,其计算公式为
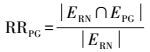 (1)
(1) 式中,ERN和EPG分别对应道路网络和邻近图的弧段数目。
(2) 邻近图构成比率(proximity graph edge ratio, PR)是衡量道路网络节点生成的邻近图与道路网络的弧段匹配程度的相对指标,是道路网络节点生成的邻近图与道路网络中相同的弧段数,与网络邻近图中的弧段数的比值。不同邻近图中和道路网络中相同的弧段数越多,该比率越大,其计算公式为
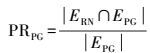 (2)
(2) 式中,ERN和EPG分别对应道路网络和邻近图的弧段数目。
(3) 全局构成比率(entire graph edge ratio, ER)反映的是道路网络节点生成的邻近图与道路网络的弧段匹配的综合程度,是道路网络节点生成的邻近图与道路网络中相同的弧段,与网络邻近图中的弧段个数的比值。该比率增加时取决于不同邻近图中与道路网络中相同的弧段数,与邻近图的弧段数的比例关系,计算公式为
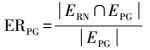 (3)
(3) 式中,ERN和EPG分别对应道路网络和邻近图的弧段数目。
(4) 网格树指数是表征道路网络类型的因子,计算公式为
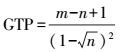 (4)
(4) 式中,n为道路网络节点个数;m为弧段个数
(5) 网络交点因子(cross factor,CF),即道路网络节点的密度与道路网络密度平方的比值,计算公式为
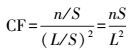 (5)
(5) 式中,n为弧段个数;S区域面积;L为道路网络长度。
由上述计算公式,结合北京道路网络数据和其网络节点生成的邻近图数据,统计结果见表 1。
| 类型 | 弧段数 | 匹配数 | RR | PR | ER | GTP | CF |
| NNG | 1193 | 1024 | 0.36 | 0.86 | 0.26 | -0.34 | 11.153 |
| MST | 1764 | 1473 | 0.53 | 0.83 | 0.32 | 0 | 3.164 |
| RNG | 2302 | 1882 | 0.67 | 0.82 | 0.37 | 0.32 | 1.227 |
| GG | 3407 | 2231 | 0.80 | 0.65 | 0.36 | 0.97 | 0.347 |
| UG | 3623 | 2240 | 0.81 | 0.62 | 0.35 | 1.11 | 0.284 |
| DT | 5225 | 2551 | 0.91 | 0.49 | 0.32 | 2.06 | 0.099 |
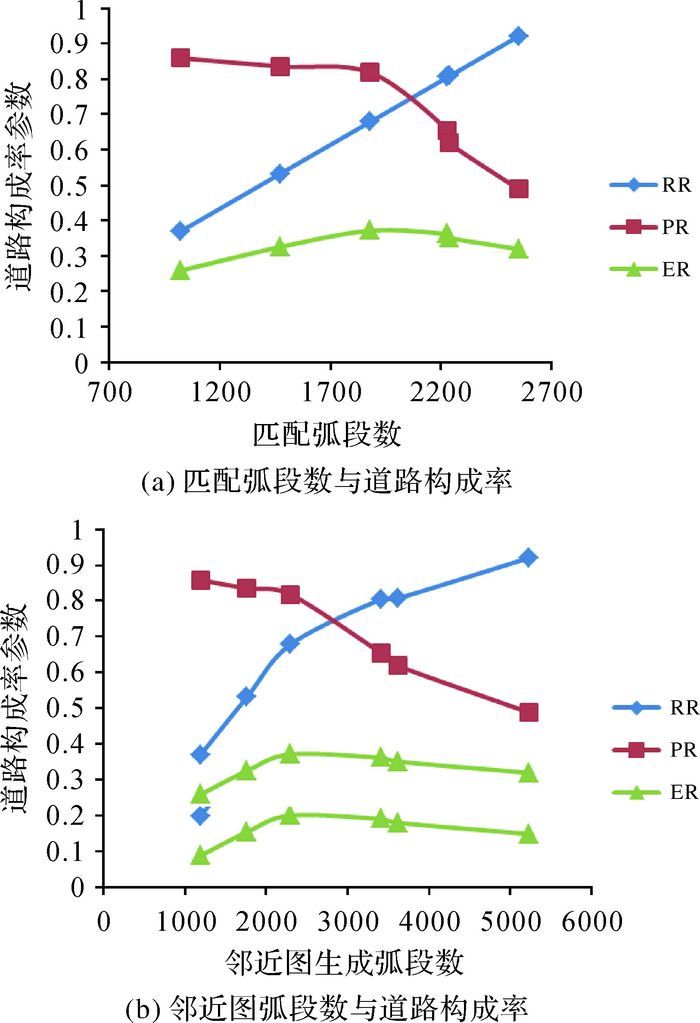
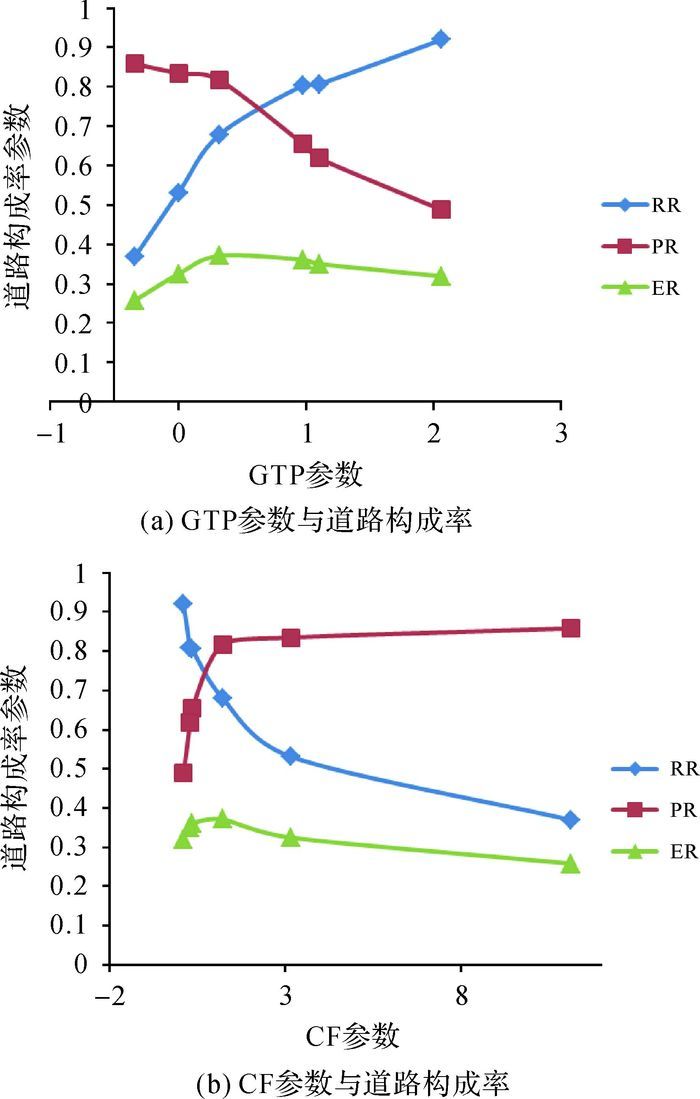
为了分析道路网络的邻近图与相关参数的关系,需要分析北京道路网络邻近图的各参数的关系。分析北京道路网络的弧段数、匹配弧段与道路构成率之间的关系,如图 3所示。分析道路的统计参数GTP、CF与道路构成率之间的关系,如图 4所示。
|
| 图 3 北京道路网络邻近图道路构成率关系 |
|
| 图 4 GTP和CF与道路网络构成率关系 |
对道路构成率的绝对比较参数RR进行分析,RR是表征基于道路网络节点与其生成邻近图的绝对参量,邻近图与道路网络匹配的弧段数目越多,其值越大。DT图生成的弧段多,其匹配到的道路网络的弧段数就大,则其道路构成率参数RR数值大。
由于RR是基于道路网络节点与其生成邻近图相对衡量参数,通过分析北京道路网络节点生成的邻近图构成率相对比较参数PR结果不难发现,NNG图的匹配弧段不多,但是其NNG图本身的弧段数目也不多,从而使得道路构成率相对衡量指标RR数值大。ER参数综合考虑了邻近图匹配的弧段数与邻近图本身的弧段数目,由计算结果可知,从这点分析,北京道路网络节点生成的RNG图的ER指数最大,在北京道路节点生成的邻近图中,RNG图最符合北京道路网络邻近特征。
分析邻近图的GTP与道路构成率的关系可知,随着GTP指数的增大,RR指数逐渐增大,PR指数随之减少,ER指数先增大后减小(拐点出现在NNG图中,NNG的ER参数值最大)。由于GTP与道路网络节点生成图的弧段和节点相关,而6种邻近图中的网络节点数相同,这样GTP的数值直接与其邻近图的弧段数目相关。由6种邻近图的包含关系可知,NNG的弧段数目最少,其GTP指数最小,DT图的弧段数目最多,从而其GTP指数最大。
分析邻近图的CF与道路构成率的关系可知,随着CF指数的减少,RR指数逐渐增大,PR指数随之减少,ER指数先减小后增大(拐点出现在NNG图中,NNG的ER参数值最大)。从CF的计算公式可看出,该参数的数值与生成邻近图的节点个数、邻近图整个区域的面积及弧段的弧段长度总和相关。由于6种近邻图有相同的节点个数、相同的面积,因此其参数数值与邻近图的长度总和成反比,邻近图DT的CF数值最低。
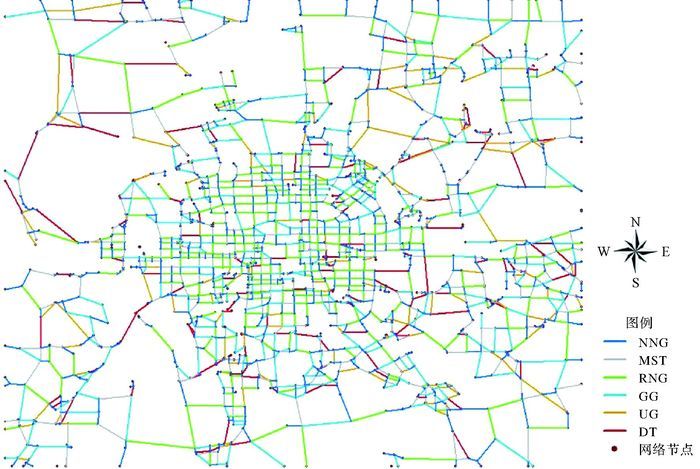
为了比较北京道路网络与基于其网络节点生成的6种类型的邻近图的匹配特征,将不同类型的邻近图按照与道路网络匹配的匹配弧段关系绘制专题图,结果如图 5所示。
|
| 图 5 道路网络邻近图匹配特征 |
从结果可以看出,基于北京道路网络节点的RNG与北京道路网络匹配度最高,北京道路网络节点的RNG与道路网络匹配的弧段密度较高部分集中在中心城区。
3 结语本文针对北京道路网络特征,基于邻近图理论,并结合道路网络参数对北京道路网络数据进行了分析研究。通过分析得出,北京道路网络节点的RNG与北京道路网络匹配度最高,从而为基于邻近图RNG进行道路网络分析(道路网络模拟、道路网络演化等)提供了理论支撑。不同城市道路网络结构不同,基于邻近图分析的道路网络特征分析结果也可能不同,分析道路网络特征需要针对道路网络数据本身的特征。在该方法的应用推广方面,基于空间索引可有效提高邻近图构成的效率。
| [1] | 路纲, 周明天, 牛新征, 等. 无线网络邻近图综述[J]. 软件学报, 2008, 19(4): 888–911. |
| [2] | 郭庆胜, 郑春燕, 胡华科. 基于邻近图的点群层次聚类方法的研究[J]. 测绘学报, 2008, 37(2): 256–261. |
| [3] | 宋晓眉, 程昌秀, 周成虎, 等. 利用k阶空间邻近图的空间层次聚类方法[J]. 武汉大学学报(信息科学版), 2010, 35(12): 1496–1499. |
| [4] | ADAMATZKY A, MARTÍNEZ G J, CHAPA-VERGARA S V, et al. Approximating Mexican Highways with Slime Mould[J]. Natural Computing, 2011, 10(3): 1195–1214. DOI:10.1007/s11047-011-9255-z |
| [5] | 蔡先华, 王炜, 戚浩平. 基于GIS的道路几何网络数据模型及其应用[J]. 测绘通报, 2005(12): 24–27. DOI:10.3969/j.issn.0494-0911.2005.12.007 |
| [6] | 莫辉辉, 王姣娥, 金凤君. 交通运输网络的复杂性研究[J]. 地理科学进展, 2010, 27(6): 112–120. |
| [7] | 田晶, 吴荡, 湛逸飞. 城市道路网的度相关性研究[J]. 武汉大学学报(信息科学版), 2014, 39(3): 332–334. |
| [8] | 王少华, 钟耳顺, 张小虎, 等. 北京交通网络拓扑结构及可达性格局历史变化研究[J]. 测绘与空间地理信息, 2014, 37(1): 9–12. |
| [9] | 方华强, 刘金林, 叶宁, 等. 城市道路网拓扑模式分析实证研究[J]. 测绘通报, 2015(S2): 89–92. |
| [10] | ADAMATZKY A. On Excitable β-skeletons[J]. Journal of Computational Science, 2010, 1(3): 175–186. DOI:10.1016/j.jocs.2010.07.003 |
| [11] | WATANABE D. A Study on Analyzing the Grid Road Network:Patterns Using Relative Neighborhood Graph[C]//The Ninth International Symposium on Operations Research and Its Applications (ISORA'10). Chengdu:[s.n.], 2010:112-119. |
| [12] | OSARAGI T, HIRAGA Y. Road Network Analysis Using Geometric Graphs of β-skeleton[C]//The 11th International Conference on Geocomputation.[S.l.]:[s.n.], 2011. |
| [13] | 吴敏君. GIS空间索引技术的研究[D]. 镇江: 江苏大学, 2006. http://book.hzu.edu.cn/334617.html |
| [14] | 张小虎, 钟耳顺, 王少华, 等. 多尺度空间格网数据的索引编码研究[J]. 测绘通报, 2014(7): 35–38. |


