2. 信息工程大学, 河南 郑州 450001
2. Information Engineering University, Zhengzhou 450001, China
对于边坡变形监测,采用全站仪和GPS等传统的测量手段进行高精度测绘工作往往费时费力,近年来快速发展的三维激光扫描技术为解决复杂的边坡地形测量提供了新的技术手段。三维激光扫描仪可以获取真实场景下高分辨率和高精度的激光点云数据,实现了对面的测量,具有诸多优势,可用于三维物体表面及地形的变形监测。其中,地面三维激光扫描仪(terrestrial 3D laser scanner,TLS)在边坡形变监测与形变分析领域得到了较多的应用,目前已有较多研究人员利用该技术进行边坡变形监测[1-3]。边坡变形监测需要获取两期及以上的点云数据进行比较,对于边坡点云数据分析比较的研究大体可分为两类:一类属于提出算法并自主编写程序进行分析[4-6],刘昌军等[7-11]取得了丰硕的成果;另一类属于借助已有点云对比分析软件进行分析比较,如Geomagic Qualify[12-14]、PolyWorks 8.0[15]、I-SITE Studio[16]、RealWorks Survey[17]。
对于复杂的边坡地形,地面起伏变化大,有些区域植被覆盖密集,TLS技术观测边坡会出现植被遮挡、点云数据采集不完整等现象,造成滤波后边坡地形点云分布不均匀、出现空洞等问题。构建表面模型操作复杂、效果差、模型存在空洞等问题会对边坡形变分析造成一定的影响。针对以上问题,本文采用Riegl VZ-1000扫描仪采集某开采沉陷区边坡两期点云数据,对点云重构与形变分析进行深入研究。
1 点云数据预处理 1.1 点云拼接在不同位置架设三维激光扫描仪进行扫描,为了得到试验区完整的点云模型,必须将不同位置扫描得到的点云数据进行拼接。点云拼接的基本原理是通过选定多个同名点解算出旋转平移矩阵实现,一般包括两个步骤:① 手动选取两次扫描中的同名特征点进行粗拼接,通常选用的点数越多拼接效果越好,一般3~5个同名点即可得到相当好的拼接效果;② 采用邻近点迭代算法(iterative closest points,ICP)进行精细拼接,通过迭代使得两点间差异随着均方差函数的最小化而减少。
1.2 点云数据坐标转换拼接完成的两期及以上的边坡点云数据需要通过坐标转换完成坐标系的统一后才能进行形变分析。采用无控制匹配的坐标转换方法,首先选择拼接完成后的两期点云数据中无形变区域的3~5个同名特征点进行粗拼接,然后对无形变区域进行ICP迭代计算,求取旋转平移矩阵,最后按照旋转平移矩阵将两期及以上的边坡点云数据进行坐标统一。
1.3 点云去噪及滤波边坡模型构建及形变分析需要比较地形的变化,非地面点是否完全去除直接关系到边坡模型的构建精度,因此需要去除噪声点,以及植被、建筑物、构筑物等非地面点。噪声点主要包括非连接项及体外孤点,选择与其他多数点保持一定距离的点作为噪声点并去除。对于植被等非地面点,采用一种基于不规则三角网的渐进加密算法对非地面点进行滤波处理,主要的滤波参数有基本网格大小、最大倾斜角等,该算法的优势在于可以有效保留地形变化特征。
2 点云数据压缩重构 2.1 反距离权重法基本原理反距离权重法是非规则分布点变成规则分布点常用的网格化方法之一。基于相近相似的原理,首先,在二维平面空间计算所有点到所求插值点的距离,离散点(xi, yi)到插值点A (x, y)的距离Di为:Di=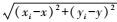
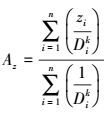 (1)
(1) 式中,Az为插值点A (x, y)的z坐标值;zi为离散点(xi, yi)的z坐标测量值;n为最近点个数;Di为离散点(xi, yi)到插值点A (x, y)的距离;k为幂指数,一般k=2。
目前反距离权重法有两种较好的实施办法,第一种是按照固定点数原则,设置距离插值点的最近点个数n,以插值点为中心搜索周围点,计算周围点到插值点的距离并进行排序,选取距离插值点最近的n个点进行反距离加权计算该插值点的z坐标值;第二种是按照固定距离原则,采用以插值点为圆心,设置半径R,选取落入圆中的点进行反距离加权计算该插值点的z坐标值。
2.2 点云压缩重构流程首先以规则二维格网划分点云数据,以点云坐标值最小值向下取整作为网格划分的起始点,分别沿着X轴方向与Y轴方向以设置的网格长宽绘制二维网格,直到网格顶点坐标最大值大于点云坐标的最大值,完成网格绘制,按照网格将点云进行划分。根据网格中的点云数据,判断点云最外轮廓线所在网格作为最外轮廓网格,取该最外轮廓网格以内的网格进行计算。
采用融合固定点数与固定距离两种原则的反距离权重法插值计算网格中心点坐标。为提高计算效率,将网格进行分块处理,以中心网格的左下角顶点作为原点,将网格沿着X轴与Y轴划分为4部分,每一部分以原点处网格作为起始网格向外进行循环计算。通过C#和OpenGL编程实现该算法,实现在极短的时间内完成点云压缩重构,为点云建模提供数据基础,具体流程如图 1所示。
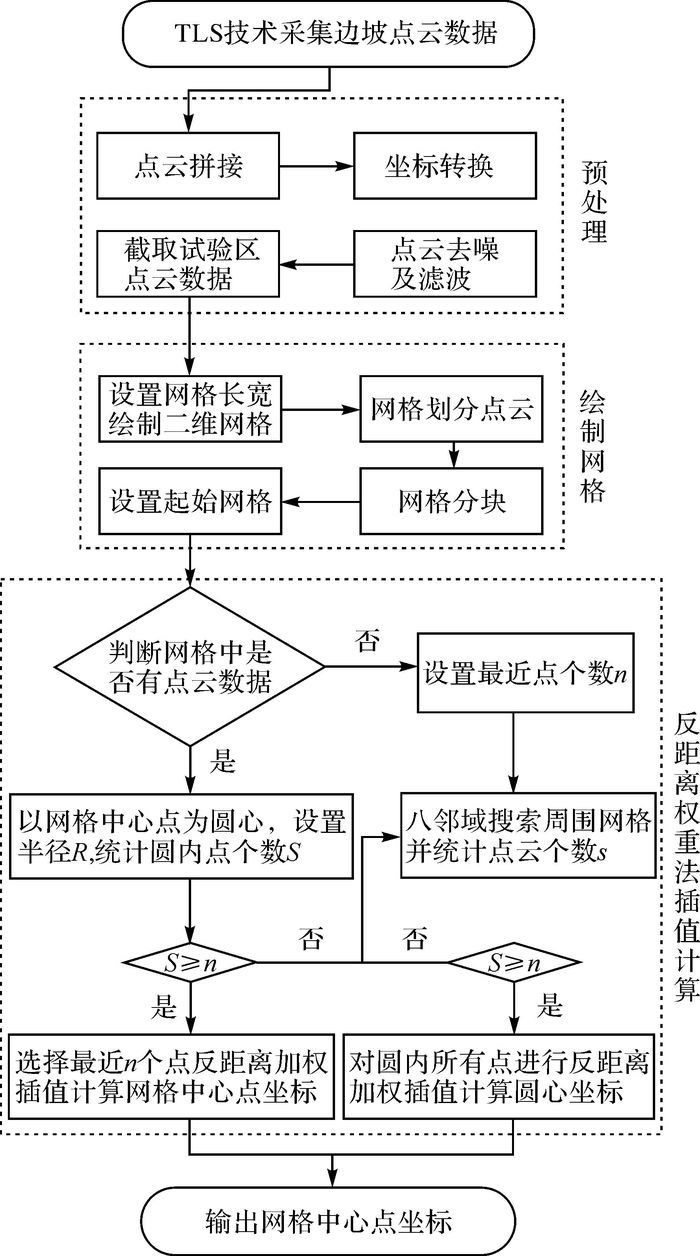
|
| 图 1 点云压缩重构流程 |
选择山西柳林某一开采沉陷区的边坡作为试验对象,利用Riegl VZ-1000三维激光扫描仪采集点云数据,第1次扫描后相隔9个月的时间再进行第2次扫描,边坡受开采沉陷的影响发生形变,获取两期边坡点云数据。边坡高42 m,坡脊线方向长145 m,垂直于坡脊线方向长200 m,两期边坡数据采集完成后对点云数据进行点云拼接及坐标统一。图 2为第一期原始边坡点云数据。点云拼接完成后进行预处理,图 3为第1期预处理边坡地形点云数据。观察发现,地形点云数据分布不均匀,尤其是中部植被较多部分,去除植被后存在较多空洞。

|
| 图 2 第1期边坡原始点云 |

|
| 图 3 第1期预处理点云 |
通过C#和OpenGL编程实现前文所述算法,设置网格长宽分别为0.5 m,最近点个数n=5,搜索半径R=0.5 m,程序运行环境是戴尔笔记本电脑Intel Core i3-2330M CPU,6 GB内存,Window 10操作系统,表 1为程序运行统计结果,图 4为第1期压缩重构的点云数据示意图。

|
| 图 4 第1期压缩重构点云示意图 |
对压缩重构后的点云数据建立三角面片模型,图 5为第1期重构后三角面片模型,与图 6未经压缩重构的第1期点云建立的三角面片模型进行对比可以看出,明显提高了模型效果,模型无空洞,且大大缩减了建模的步骤与时间,提高了建模效率。将三角面片模型转换为NURBS (Non-Uniform Rational B-Splines)曲面模型,与常见的三角面片模型相比,非均匀有理B样条曲面特别适用于创建复杂的曲面模型。

|
| 图 5 重构后三角面片模型 |

|
| 图 6 无重构三角面片模型 |
将两期曲面模型进行3D比较,如图 7所示。颜色偏差可以直观地看出边坡整体发生了形变,通过色谱直方图可以看出变化量集中在-0.8~-0.5 m,局部地区变化大,统计得出最大变化量为-5.24 m,原因是开采沉陷造成边坡底部发生塌陷出现了较大变化。

|
| 图 7 3D比较结果 |
在3D比较的结果上选择点进行分析,如图 8所示,A03—A06处偏差处于-0.8~-0.5 m之间,表现出整体的变化大小;根据3D比较结果选择变化大的区域,如图选择A07—A09位置,可以看出偏差变化大,反映出局部位置出现较大的形变。
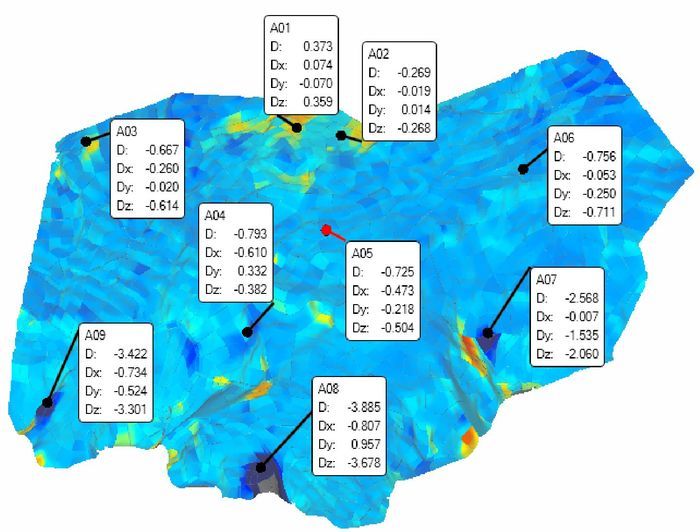
|
| 图 8 注释分析 |
选择沿着山脊线方向A—a与垂直于山脊线方向B—b创建两条二维横截面,图 9为剖面位置,图 10为剖面分析结果。A—a剖面最大形变量为-1.122 m,形变集中于-0.7~-0.5 m,B—b剖面最大形变量为-1.376 m,形变集中于-0.1~-1.8 m,整体形变较为均匀,呈现下沉趋势,符合开采沉陷影响结果。分别均匀选择5个点进行标注,高质量的边坡模型将边坡地形起伏变化情况非常良好地表达出来,边坡起伏变化造成不同位置形变呈现差异变化。
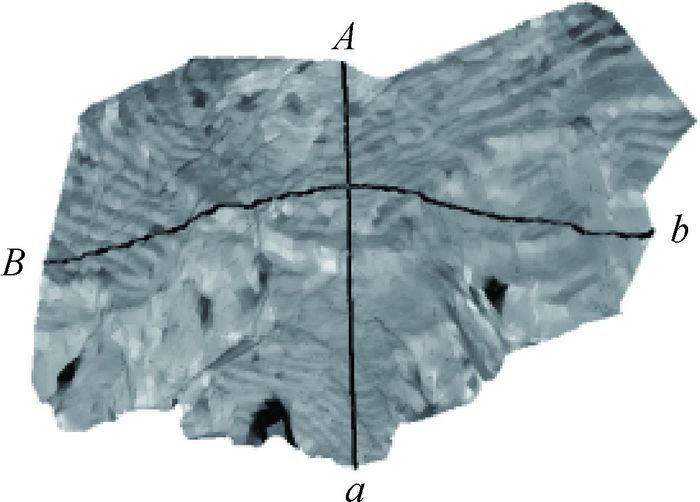
|
| 图 9 剖面位置 |
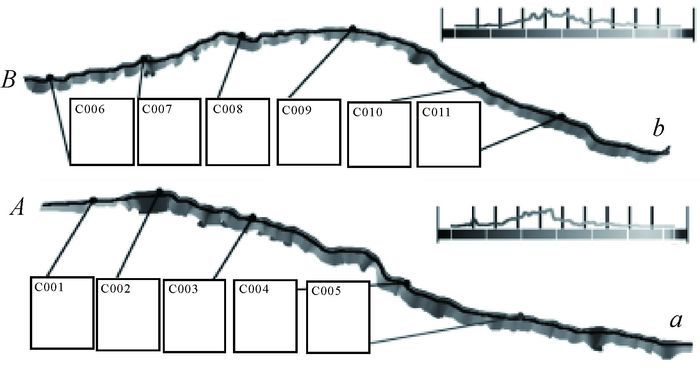
|
| 图 10 剖面分析结果 |
为了验证边坡点云压缩重构结果与求取的形变结果的准确性,需要对求取结果进行精度分析。首先输出图 10中C001—C011的详细信息,手动选取Riegl VZ-1000采集的两期边坡点云中对应的坐标点,计算形变结果。ΔX、ΔY、ΔZ表示X、Y、Z方向偏差,D表示曲面模型计算的整体偏差结果,D′表示手动选取点云中的对应坐标点计算整体偏差结果,表 2为统计结果。
| 名称 | 第1期坐标值/m | 曲面模型计算偏差/mm | 点云选点计算偏差/mm | D′-D/mm | ||||||||||
| X | Y | Z | ΔX | ΔY | ΔZ | D | ΔX | ΔY | ΔZ | D′ | ||||
| C001 | -779.976 | -356.657 | -97.454 | 26 | -14 | -250 | -251 | 42 | -21 | -240 | -245 | 6 | ||
| C002 | -766.945 | -349.365 | -96.197 | 33 | -93 | -971 | -976 | 26 | -101 | -964 | -970 | 6 | ||
| C003 | -748.532 | -340.083 | -103.370 | -350 | -267 | -651 | -786 | -202 | -153 | -823 | -861 | -75 | ||
| C004 | -718.164 | -325.398 | -120.644 | -364 | -235 | -305 | -530 | -231 | -121 | -432 | -505 | 25 | ||
| C005 | -695.738 | -314.130 | -129.694 | -19 | -86 | -660 | -666 | -24 | -93 | -729 | -735 | -69 | ||
| C006 | -706.207 | -422.724 | -130.997 | -288 | 216 | -725 | -810 | -74 | 202 | -715 | -747 | 63 | ||
| C007 | -717.531 | -397.283 | -121.545 | -401 | 378 | -835 | -1001 | -449 | 557 | -741 | -1030 | -29 | ||
| C008 | -729.025 | -370.699 | -110.249 | -70 | -224 | -795 | -829 | -82 | -384 | -681 | -786 | 43 | ||
| C009 | -743.664 | -340.668 | -104.431 | -217 | 61 | -773 | -805 | 209 | 72 | -830 | -859 | -54 | ||
| C010 | -765.970 | -305.667 | -119.662 | 8 | -313 | -665 | -735 | -2 | -299 | -639 | -705 | 30 | ||
| C011 | -779.371 | -284.083 | -127.567 | -69 | -295 | -953 | -1000 | -82 | -311 | -984 | -1035 | -35 | ||
对手动选取计算得出的形变结果与图 10中选取点的形变结果进行一致性检验,采用μ-检验法进行假设检验。计算曲面模型求取的整体偏差结果D与手动选取对应点计算整体偏差结果D′的差值D′-D,可求取均值μ=-8.1 mm,标准差为σ=±44.898 mm。计算得到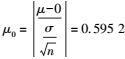
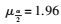
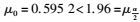
利用三维激光扫描仪采集边坡点云数据进行边坡变形监测,与传统测量相比具有诸多优势。针对边坡地形点云数据分布不均匀、存在空洞、直接建立边坡模型并进行形变分析效果差的问题,本文提出了一种点云快速压缩重构的方法,并编程实现了自动化处理;经过试验验证,该方法能够解决问题且快速高效完成点云重构,为边坡模型构建提供了良好的数据基础。
利用重构后点云能够明显提高建模效率,简化了建模步骤,提高了建模效果,NURBS曲面更好地表达了复杂地形的起伏变化,为形变对比分析提供了准确的模型数据。利用曲面模型进行边坡形变对比分析,从面、线、点3个方面全面分析了某矿区边坡的形变情况,对形变结果进行了一致性分析,符合实际地形变化情况。本文的研究为三维激光扫描技术进行边坡变形监测提供了支持。
| [1] | 赵小平, 闫丽丽, 刘文龙. 三维激光扫描技术边坡监测研究[J]. 测绘科学, 2010, 35(4): 25–27. |
| [2] | 朱龙元, 杨智翔. 基于三维激光扫描的滑坡信息提取方法研究[J]. 人民长江, 2016, 47(17): 53–55. |
| [3] | 谢谟文, 胡嫚, 杜岩, 等. TLS技术及其在滑坡监测中的应用进展[J]. 国土资源遥感, 2014, 26(3): 8–15. DOI:10.6046/gtzyyg.2014.03.02 |
| [4] | 李崇瑞, 张锦, 肖杰. 应用TLS点云数据确定边坡特征对象区域和形变分析[J]. 测绘通报, 2016(7): 94–97. |
| [5] | 谢建春, 姚吉利, 马宁, 等. 基于坡度梯度的点云数据中坡坎探测方法研究[J]. 测绘地理信息, 2015, 40(6): 53–56. |
| [6] | 徐进军, 王海城, 罗喻真, 等. 基于三维激光扫描的滑坡变形监测与数据处理[J]. 岩土力学, 2010, 31(7): 2188–2191. |
| [7] | 刘昌军, 丁留谦, 孙东亚. 基于激光点云数据的岩体结构面全自动模糊群聚分析及几何信息获取[J]. 岩石力学与工程学报, 2011, 30(2): 358–364. |
| [8] | 刘昌军, 高立东, 丁留谦, 等. 应用激光扫描技术进行岩体结构面的半自动统计研究[J]. 水文地质工程地质, 2011, 38(2): 52–57. |
| [9] | 刘昌军, 刘会玲, 张顺福. 基于激光点云直接比较算法的边坡变形监测技术研究[J]. 岩石力学与工程学报, 2015, 34(S1): 3281–3288. |
| [10] | 刘昌军, 赵雨, 叶长锋, 等. 基于三维激光扫描技术的矿山地形快速测量的关键技术研究[J]. 测绘通报, 2012(6): 43–46. |
| [11] | 岳冲, 刘昌军, 王晓芳. 基于多尺度维度特征和SVM的高陡边坡点云数据分类算法研究[J]. 武汉大学学报(信息科学版), 2016, 41(7): 882–888. |
| [12] | 褚宏亮, 殷跃平, 曹峰, 等. 大型崩滑灾害变形三维激光扫描监测技术研究[J]. 水文地质工程地质, 2015, 42(3): 128–134. |
| [13] | 马俊伟, 唐辉明, 胡新丽, 等. 三维激光扫描技术在滑坡物理模型试验中的应用[J]. 岩土力学, 2014, 35(5): 1495–1505. |
| [14] | 杨帆, 李龙飞, 吴昊. 基于三维激光扫描的边坡变形数据提取研究[J]. 测绘工程, 2016, 25(10): 1–4. |
| [15] | 董秀军, 黄润秋. 三维激光扫描技术在高陡边坡地质调查中的应用[J]. 岩石力学与工程学报, 2006, 25(S2): 3629–3635. |
| [16] | 刘明坤, 段奇三, 赵晨曦, 等. 三维激光扫描在滑坡灾害变形中的监测应用[J]. 测绘通报, 2016(2): 147–149. |
| [17] | 邢正全, 邓喀中. 三维激光扫描技术应用于边坡位移监测[J]. 地理空间信息, 2011, 9(1): 68–70. |



