2. 中国矿业大学环境与测绘学院, 江苏 徐州 221116;
3. 华东交通大学理工学院经济管理分院, 江西 南昌 330100
2. School of Environment and Spatial Mapping, CUMT, Xuzhou 221116, China;
3. Economic Management Branch, ECJTUIT, Nanchang 330100, China
近年来,针对建筑物倒塌、城镇火灾、地震等灾害场景应急定位难题,基于传统定位精度因子的单因子静态基站组网方式已难以兼顾灾害场景和环境信息的自组网体系[1]。然而灾情空间分布情况及不同灾情程度的发生位置,是搜救人员实施任务的主导环节,因此导航定位技术在灾害状况分布图的制作和救援决策中具有不可替代的作用[2]。基于传感器的室内定位原理与全球定位系统伪距定位原理相似,终端至少需要接收4个基站传输的信号才能完成定位[3]。在矿井、失火大楼等灾害环境中,由于该方式定位涉及信号多重覆盖、区域信号的连续性、信号延迟等问题[4],基站位置的确定将直接影响区域内的定位效果。因为受上述因素的影响,基站坐标确定问题属于优化问题中的组合优化问题。当前主要组网方式有星型布设、方形布设和菱形布设[5],但其设计方案过于理想化,没有考虑定位区域的空间特征,在实际应用中难以满足实际需求,一般不是最佳布站方案。
曾有学者提出,将生物学中的遗传模型应用于雷达网的优化布设[6]。遗传算法(genetic algorithm,GA)作为现代智能优化算法,最大特点是可以针对非线性优化问题快速挑出局部最优解[7]。由于GA算法容易发生过早收敛现象,算法的最优解依赖于初始种群现象较严重,使得算法需经过长时间才能得到最优解[8]。应急组网属于动态组网,目前还没有一套综合的组网理论。鉴于此,本文提出应急组网遵循的基本原则,并结合IAGA模型将其应用到基站组网优化部署中,该模型从种群的选取,到遗传过程操作中均有改良。试验证明,该算法能够较大提高组网效率,为实施决策提供一定的参考价值。
1 优化组网的数学模型 1.1 测距定位算法 1.1.1 时间差定位(TDOA)算法假定灾区中一点的空间三维坐标为(X,Y,Z),它到第一个固定基站(X0,Y0,Z0)与移动站(Xi,Yi,Zi)的传播时间和距离差分别为t0、ti和ΔRi(i=1,2,3),则有如下关系方程组成立,以ΔRi作为观测值得到观测方程
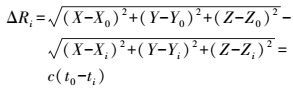 (1)
(1) 以灾区点的空间位置作为未知量,对式(1) 进行一阶泰勒级数展开,TDOA测量可以写为
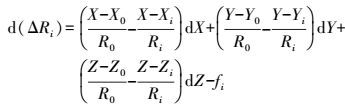 (2)
(2) 写成矩阵形式有
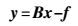 (3)
(3) 式中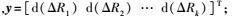
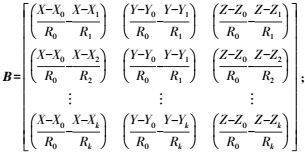
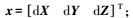
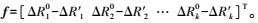
其中,ΔRk0为观测值;ΔR′k为推算的观测值近似值。
根据间接平差原理:
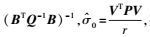
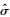
 (4)
(4) 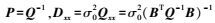
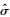
(1) 定义平面位置精度因子[3]
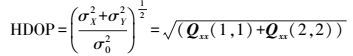 (5)
(5) (2) 高程精度因子[3]
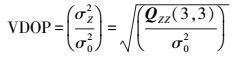 (6)
(6) (3) 空间位置精度因子[3]
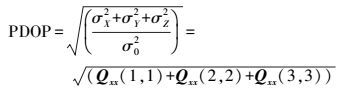 (7)
(7) 一个具体的现场组网部署任务,事故现场的自然条件(地物、地貌)已经确定。如多层式的办公楼可以将受灾区域分为重点定位区域、一般定位区域和较安全区域。火势较重、人口密集的危险楼层可设置为重点定位区域;受灾程度较轻、人口稀少的楼层可设置为一般定位区域;暂时安全、无人区的楼层可以设置为较安全区域。基站优化部署应该遵循连续性、区域重叠性、可靠性、探测区域最大化原则[10]。优化部署基站原则量化如下[11]:
(1) 连续性:终端处于目的基站接发射信号的有效半径内,才能保证数据的可靠性。假设每个基站的通信半径为Ri,终端位置点j至基站i的距离为dij,则有
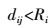 (8)
(8) (2) 区域重叠性:终端只有获得其与足够数目的基站之间的距离测量值,才能完成定位,实现应急组网的功能,即有
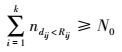 (9)
(9) 式中,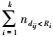
(3) 可靠性:为了提高终端定位跟踪进度,要求区域中任一点DOP值小于相应阈值,即有
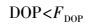 (10)
(10) 式中,DOP可以是HDOP (平面精度因子)、VDOP (高程精度因子)或PDOP(空间位置精度因子),对应FDOP分别为FHDOP(平面精度因子阈值)、FVDOP(高程精度因子阈值)或FPDOP(空间位置精度因子阈值)。
(4) 探测区域最大化:基站组网对责任区的覆盖范围也尽可能大,整体覆盖层数尽可能多。
覆盖区网络由N部基站组成,改变基站放置位置,网络的性能将会发生较大程度的变化,寻求一组合适的基站坐标对网络进行优化,使得在该区域中加权DOP值达到最小,以最差DOP值点位个数最少为目标,使其达到定位设计要求。目标函数可表示为
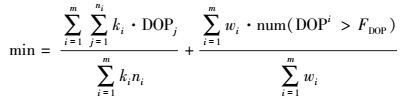 (11)
(11) 式中,m为分区域的类型数目;ni为对应的区中特征点个数;ki为区域DOP加权值;num (DOPi>FDOP)表示区域i中特征点DOP值超越FDOP的个数;wi为区域中DOP越值的加权值,即目标函数越小,个体的适应度越大。
2 改进的自适应遗传算法组网优化部署 2.1 编码方式一般来说,染色体编码方式有浮点编码、二进制编码、格雷码编码、符号编码法[12]。鉴于浮点数编码可表示的数值较大、精度高且便于较大空间的遗传搜索,可以较好地应用于本问题,依次将基站的空间坐标设置为染色体,采用浮点编码方式[13],各基站的三维坐标分别由nx、ny和nz位的十进制编码表示,多基站组成的染色体编码表示如图 1所示。

|
| 图 1 遗传编码解析 |
初始种群规模应足够大,以增加取得最优解的概率,但规模过大易造成搜索范围过大,遗传过程时间变长。文献[14]提出一种基于星型布站方式实现三维定位的方法,其基站组网方式可以作为初始种群的预选值,并结合Hamilton算法获得一个较合适的初始种群。
2.3 基于Logistic的随机交叉操作这里的交叉操作采取“门当户对”的形式,即适应度接近的父代个体相互配对。交叉点位置通过Logistic序列确定,对需要配对的父代进行交叉操作。在实际操作时,是通过产生一个服从(0, 1) 均匀分布的随机数,如果该值大于交叉概率Pc,则在相应个体的Logistic点位上进行交叉配对。
2.4 基于种群规模的变异操作在进行交叉过程之后,从新个体中选择变异个体,变异个体和个体基因位置采取随机的方式进行。变异数量由群体中的群体个数N和变异概率Pm决定,并有
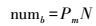 (12)
(12) 与交叉操作方式类似,在实际操作时,通过产生一个服从(0, 1) 均匀分布的随机数,若该值小于变异概率Pm,则在相应个体的Logistic点位上进行变异操作。
2.5 交叉概率和变异概率的自适应优化对交叉概率和变异概率进行自适应修正,使得变异和交叉操作随着子代适应度自适应调整[15],其表达式如下
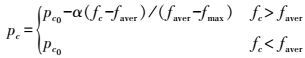 (13)
(13) 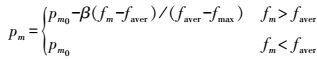 (14)
(14) 式中,pc0和pm0为常数,分别表示初始交叉概率和初始变异概率;α和β为区间[0,1]的常量;fc为交叉个体适应度大的个体适应度;fm表示变异个体的适应度;faver表示所有个体中的平均适应度;fmax表示所有个体中的最大适应度。
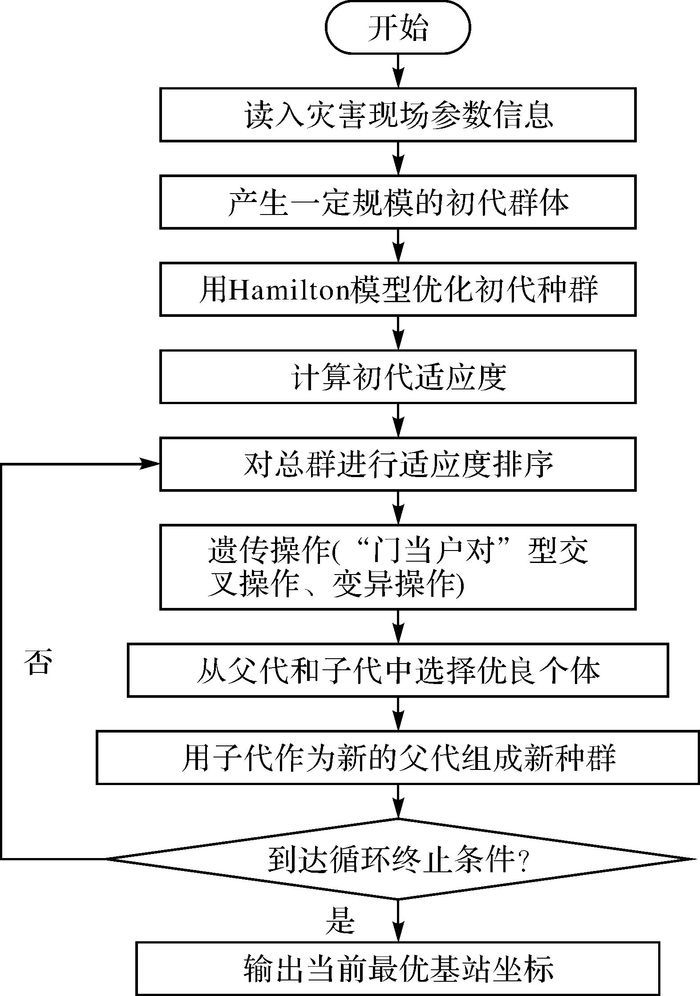
2.6 算法流程灾害优化组网布设的改进自适应遗传算法的主要步骤流程如图 2所示。
|
| 图 2 IAGA算法流程 |
假定布设区域为100 m×100 m×20 m的长方体空间,3类不同的等级定位区域。定位系统共由4个基站组成,其中1个固定基站、3个可移动基站。3类不同等级定位区域的高度不同,分别为2.5~7.5 m、7.5~12.5 m、12.5~17.5 m。基站最大感应半径为200 m,其中固定站坐标为(150,150,20),3个移动站分布于空间外侧。
改进自适应遗传算法参数设置如下:染色体长度L=30,种群规模值取N=50,初始交叉概率值pc0为0.95,初始变异系数值pm0取为0.1,在适应度函数中,FPDOP取为12,区域DOP加权值k={1, 2, 3},区域DOP越值的加权值w={1, 2, 3}。通过改进自适应遗传算法对移动基站坐标进行优化计算,运算结果见表 1。
| 迭代次数 | 基站1坐标/m | 基站2坐标/m | 基站3坐标/m | 函数值fp | ||||||||
| x | y | z | x | y | z | x | y | z | ||||
| 5 | 25.8 | 116.9 | 1.1 | 130.1 | 253.0 | 2.5 | 203.3 | 56.9 | 0.5 | 5.720 | ||
| 10 | 54.0 | 140.2 | 1.4 | 169.2 | 239.0 | 2.3 | 223 | 86.8 | 0.8 | 5.589 | ||
| 20 | 45.9 | 111.4 | 1.1 | 156.8 | 246.6 | 2.4 | 227.1 | 78.5 | 0.7 | 5.081 | ||
| 30 | 49.1 | 107.2 | 1.0 | 197.1 | 235.3 | 2.3 | 211.3 | 45.8 | 0.4 | 4.637 | ||
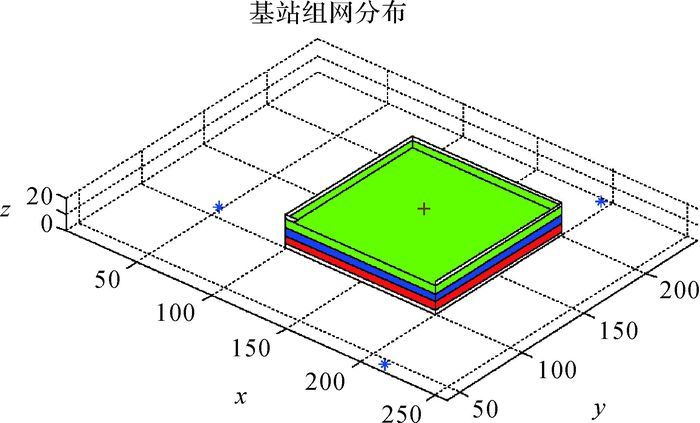
图 3为经过算法优化之后的组网效果图,其中“+”形状图样为固定基站,“*”形状图样为移动基站,深灰色区域为较安全区域(高度2.5~7.5 m),黑色区域为一般定位区域(高度7.5~12.5 m),浅灰色区域为重点定位区域(高度12.5~17.5 m)。
|
| 图 3 基站组网示意图 |
同时,将表 1迭代30次结果与蚁群算法迭代60次及传统遗传算法迭代30次得到的结果进行比较。蚁群算法的优化结果为:移动基站1位置(48.5,105.8,0.9),移动基站2位置(197.2,234.9,2.0),移动基站3位置(211.2,45.6,0.5),目标函数值fp为4.703。传统遗传算法的优化结果为:移动基站1位置(54.4,140.9,1.4),移动基站2位置(159.2,239.9,2.3),移动基站3位置(224,86.8,0.80),目标函数值fp为5.602。
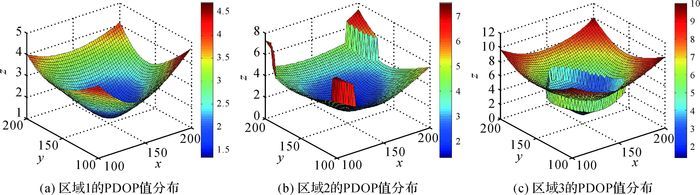
分别选取区域中的高度为5、10和15 m的区域面作为3类不同等级区域特征面,经过改进的自适应遗传算法迭代30次运算得到基站坐标,组成的基站网在不同类型等级定位区域的PDOP值分布如图 4所示。使用蚁群算法和传统遗传算法得到的在不同类型等级定位区域的PDOP值分布,如图 5和图 6所示。

|
| 图 4 改进的自适应遗传算法的区域PDOP值分布 |
|
| 图 5 蚁群算法的区域PDOP分布 |
|
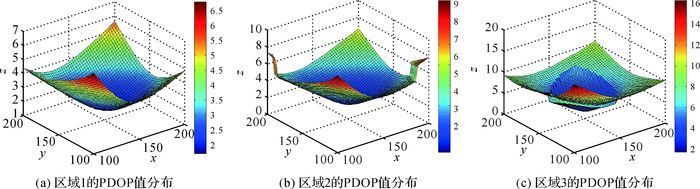
| 图 6 传统遗传算法的区域PDOP分布 |
表 2为3种算法在3个特征面上的平均PODP值(aver)、最小PDOP值(min)和最大PDOP值(max)3个指标的比较。
| 区域PDOP | 改进自适应遗传算法 | 蚁群算法 | 传统遗传算法 | ||||||||
| aver | min | max | aver | min | max | aver | min | max | |||
| 5 m | 2.717 5 | 1.335 1 | 4.702 3 | 2.716 5 | 1.337 9 | 4.713 4 | 3.366 2 | 1.721 0 | 6.786 1 | ||
| 10 m | 3.389 9 | 1.329 4 | 7.631 5 | 3.391 7 | 1.332 2 | 7.556 6 | 4.153 1 | 1.713 3 | 9.174 9 | ||
| 15 m | 5.964 0 | 1.323 6 | 9.980 2 | 5.990 9 | 1.342 6 | 10.031 1 | 6.852 9 | 1.706 0 | 16.257 7 | ||
由图 4—图 6和表 2可知,改进的自适应遗传算法相较于蚁群算法从效率上有较大程度的提升,性能也有所提高。相较于传统的遗传算法,由于初始种群的改良、交叉变异的改进,使得搜索速率加快,大大节省了寻求最优解的运算时间,提高了应急网络综合性能。
4 结语本文提出了一种改进的自适应遗传算法,并将其应用于应急定位组网的基站优化部署。根据应急定位的特殊性,结合基站组网的特点,总结出优化组网的概念、遵循的原则及组网的评价指标。试验结果表明,该算法能够达到应急定位精度的要求,满足灾害环境下的定位要求,符合组网基本原则。为了加快算法收敛速度,提高组网强度,通过改良圈算法和Logistic混沌序列改良父代种群,以及遗传操作中的变异与交叉自适应调整,其效果优于蚁群算法和传统遗传算法。
然而,在组网部署的过程中,灾害环境等自然环境因素不同,对于信号传输的非视距问题、信号干扰等因素,本文未考虑,只对其进行了简化。对于地形复杂、条件烦琐的情况还需要进一步考虑遗传模型中的参数设置、适应度函数的确定等问题。
| [1] | 蔡红. 基于UWB的定位方法研究[M]. 北京: 北京邮电大学出版社, 2014. |
| [2] | 曲国胜, 赖俊彦, 宁宝坤. 卫星定位导航系统在地震应急救援中的应用[J]. 震灾防御技术, 2007, 2(4): 409–415. DOI:10.11899/zzfy20070410 |
| [3] | 侯全武, 王坚, 胡洪, 等. 传感器位置对狭长空间定位精度的影响[J]. 大地测量与地球动力学报, 2013, 33(1): 117–122. |
| [4] | 景博. 智能网络传感器与无线传感器网络[M]. 北京: 国防工业出版社, 2011. |
| [5] | 钱镱, 陆明泉, 冯振明. 基于TDOA原理的地面定位系统中HDOP的研究[J]. 电讯技术, 2005(4): 135–138. |
| [6] | YU H F. Designing an Accelerated Degradation Experiment with a Reciprocal Weibull Degradation Rate[J]. Journal of Statistical Planning and Inference, 2006, 136(1): 282–297. DOI:10.1016/j.jspi.2004.06.030 |
| [7] | 邢文训, 谢金星. 现代优化算法[M]. 北京: 清华大学出版社, 1999. |
| [8] | NELSON W B. Graphical Analysis of Accelerated Test with a Mix of Failure Modes[J]. IEEE Transactions on Reliability, 1975, 23(3): 230–237. |
| [9] | 刘大杰, 施一民, 过静珺. 全球定位系统GPS的原理与数据处理[M]. 上海: 同济大学出版社, 2003. |
| [10] | 张远, 方青, 曲成华. 基于遗传算法的组网雷达优化部署[J]. 雷达科学与技术, 2014, 12(1): 76–80. |
| [11] | 陈亮, 邹鹏, 郝利云, 等. 基于改进蜂群算法的雷达组网优化布站研究[C]//Proceeding of Asia-Pacific Youth Conference on Communication. [S. l. ]: [s. n. ], 2011. |
| [12] | 曹博, 刘文评, 李承尚, 等. 自适应遗传算法在ADS_S优化布站中的应用[J]. 电光与控制, 2015, 22(6): 81–85. |
| [13] | 杨仕明, 柯炳清, 薛正辉. 基于遗传算法的区域雷达网优化布站方法[J]. 北京理工大学学报, 2005, 25(6): 534–537. |
| [14] | 高虎, 俞志强. 基于四站时差定位原理的星型布站分析[J]. 军雷达学院学报, 2004, 18(3): 22–24. |
| [15] | 于光帅, 于宪. 一种改进的自适应遗传算法[J]. 数学的实践与认识, 2015, 45(19): 259–264. |


