2. 合肥工业大学, 安徽 宣城 242000
2. HeFei University of Technology, Xuancheng 242000, China
数字高程模型(digital elevation model,DEM)从1958年提出至今,已经成为地形的数字描述和空间模拟的数据基础,为数字地球的发展提供了数据支持[1]。目前获取DEM方法多样,可以从航空影像、遥感图像及现有地形图中得到。由于DEM的数据来源、生产方式、内插公式等存在差异,以及操作流程中可能存在的不规范操作,会导致DEM与地理对象的地形特征不符现象,如面状水域、人工平地等这类属于平面结构地形的地理对象出现“平地不平”的失真现象[2-5]。
为了提高DEM精度,众学者作了很多此类研究,提出过不同的减少误差的方法[6-13],但大多是从DEM生产过程中提高DEM精度,对已经失真的DEM却没有一个很好的修复策略。本文针对诸如“平地不平”这类规则地形的失真现象,结合规则地形的地形特征与失真DEM的数据分布特点,提出用地形特征约束DEM形态结构,并用参数估计算法求得符合地形起伏状态的结构表达式,进而修复失真数据的方法,以求得到更高精度的DEM数据。
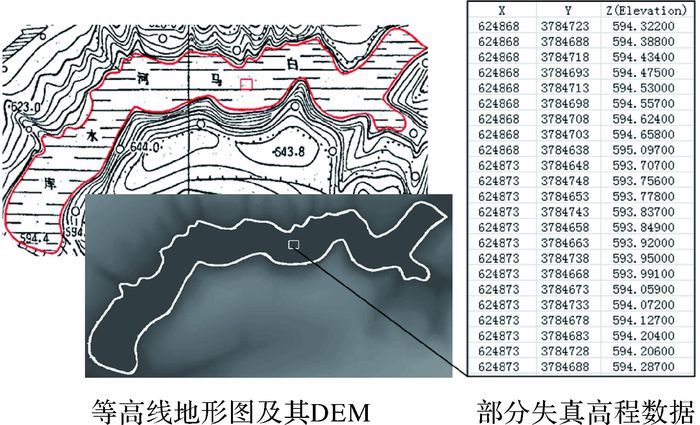
1 问题解析失真的DEM通常不能充分且确切地反映原地形的整体特征,即地理对象的地形特征,包括地形的高低起伏状态、陡缓程度等。如图 1所示,所选样区为一大型水库,其地形特征为平面结构,水域高程应相等或线性变化,但从图 1失真高程数据中可以看出,样区高程并不相等且无规律变化,该处数据明显失真。
|
| 图 1 样区地形图与失真DEM |
对此类地形失真现象进行总结,具有以下特点:① 失真区域为规则地形,地形特征可用数学公式表示,如图 1中所选的水库样区所属的平面结构地形,在数学中可以用三维平面方程表示;② 失真数据虽然存在误差,但数据整体依然在真值附近的可信范围内波动,可能存在极少数异常值,但所占比例可以忽略不计。图 1中DEM高程数据虽然存在误差,但与等高线标识的高程值进行比较,其依然在合理范围内波动。
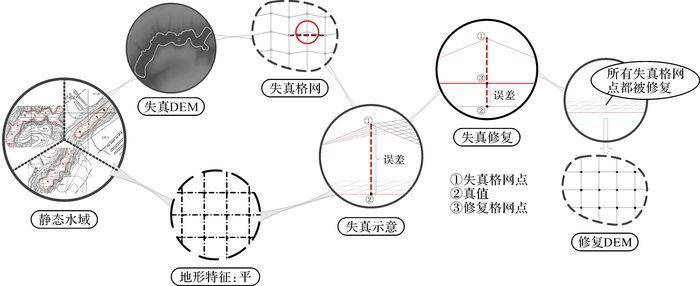
结合以上两个特点,对规格地形失真DEM进行修复的思路如图 2所示,规则地形特征所对应的数学公式描述的是DEM真值应具有的形态结构,失真格网点分布在真值附近的可信范围内,对其进行修复就是要使其整体符合地形特征且图中标识的误差尽可能小。运用参数估计算法(修复算法)求取失真DEM的高程真值近似表达式,再根据此表达式求得修复格网点,进而可得更高精度的DEM数据。
|
| 图 2 失真DEM修复示意图 |
地形特征约束了失真DEM整体形态结构,修复算法则可求出此结构的具体表达式,但不同修复算法求取的表达式不尽相同,修复后的数据精度也不同。为了得到精度更高,更能反映地形特征的DEM数据,本文选取最小二乘法(least square method,LS)与随机抽样一致性算法(random sample consensus,RANSAC)进行修复试验,并对修复结果进行比较。在处理失真问题时,LS是运用最广泛的参数估计算法之一[14-16],其原理为利用观测向量的残差平方和最小来求取模型参数,进而求得修复值。但LS虽然考虑了误差因素,却不能规避异常数据对参数的影响(DEM中常表现在部分格网点的高程突变),为此,本文选取了能够提高数据精度、减小异常数据对模型参数干扰的RANSAC与LS进行对比试验[17-19],并对修复结果进行了质量检测,比较出最优的修复算法。
2 修复方法 2.1 修复流程由于样区高程真值不可得,且抽样具有随机性,小样本不具有普适性,为了方便对修复后的DEM数据进行质量检测,以及避免采样过少可能导致的结论偏差,本文首先用模拟数据代替采样数据进行修复试验,找到更好的修复算法,再用采样数据对结论进行验证。
对失真DEM数据进行数学模拟时,针对平地地形,在三维平面上模拟了一组平面规则格网点,将此三维平面视为DEM真值平面,再为这组格网点高程添加误差向量,将未添加误差的格网数据视为DEM真值数据,含有误差的视为失真DEM数据,采用LS与RANSAC对此模拟数据进行修复。运用两种算法进行修复试验,可得两个不同修复平面方程,根据这两个平面方程可以得到不同的修复DEM数据。
为了对这两种算法的修复效果进行评估,分别求出所得的两组平面与DEM真值平面之间的夹角及修复后所得DEM的精度(本文通过修复前后数据高程中误差大小进行判断),根据夹角的大小及每种算法修复后所得数据精度,比较两种算法的优劣性,找出最优修复算法。
2.2 修复算法 2.2.1 采用最小二乘法进行修复最小二乘法成立的前提是自变量为真值矢量[20],对于DEM数据而言,当其平面向量的平面位置呈规则格网排列时,常将其平面坐标省略,只保留含有一维向量序列的高程数据(格网DEM)[1]。因此,用LS修复失真DEM数据时可以将其平面位置向量视为真值矢量,只需考虑高程Z方向上的误差情况,解算相应参数。
假设平面样区对应的三维平面方程为[20]
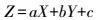 (1)
(1) 式中,a、b、c为未知参数。
对失真DEM进行处理,得到n个格网点,可表示为
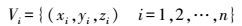 (2)
(2) 根据最小二乘原理,修复失真DEM应使S值最小,即
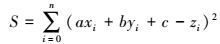 (3)
(3) 需满足式(4),即使式(5) 成立。
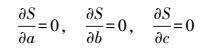 (4)
(4) 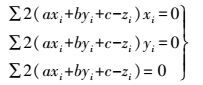 (5)
(5) 整理可得
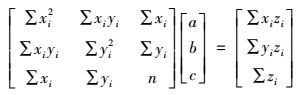 (6)
(6) 解方程组得到参数a、b、c。
2.2.2 采用随机抽样一致性算法进行修复随机抽样一致性算法由Fishchler和Bolles于1981年提出,是用于从观测数据中估计出数学模型参数的迭代算法。RANSAC的思想是假定观测数据中含有内点(inliers,对估计模型参数有用的点),也包含异常数据外点(outliers,偏离正常范围很远,不符合数学模型的数据),并且这组数据受噪声影响,RANSAC认为只要存在inliers数据点,就能估计出数学模型。其不同于LS等参数估计方法利用所有观测数据估计模型参数后再舍去误差较大的点,而是利用满足条件的尽可能少的数据并用一致性数据集将其逐渐扩大,摒弃异常数据。
用RANSAC对平面结构地形的失真DEM数据进行修复的基本步骤如下[6]:
(1) 在失真格网点中先任取3个格网点构成一个平面,并遍历其他格网点,计算每个格网点到此平面的距离。
(2) 设定阈值,当小于阈值时,认为此格网点为内点,所有内点构成一个一致集(consensus set)。
(3) 重复以上过程,重新随机抽取新的一致集。在完成一定的抽样次数后,若未找到一致集则算法失败,否则在所有一致集中选取最大一致集。
(4) 根据判断内外点并采用LS对最大一致集中所含的内点进行参数估计得到模型,算法结束。
3 试验与分析 3.1 用模拟数据进行试验在一般情况下,若随机采样点超过30个,可以认为误差服从正态分布[1],样区格网点数量远大于30个,故可认为样区DEM误差服从正态分布,对样区DEM进行数学模拟时可进行如下操作。
(1) 在平面Z=X+Y上模拟出100个规则格网点({(xi, yi, zi) i=1, 2, …, 500},如图 3(a)所示),将此平面DEM视为真值平面。
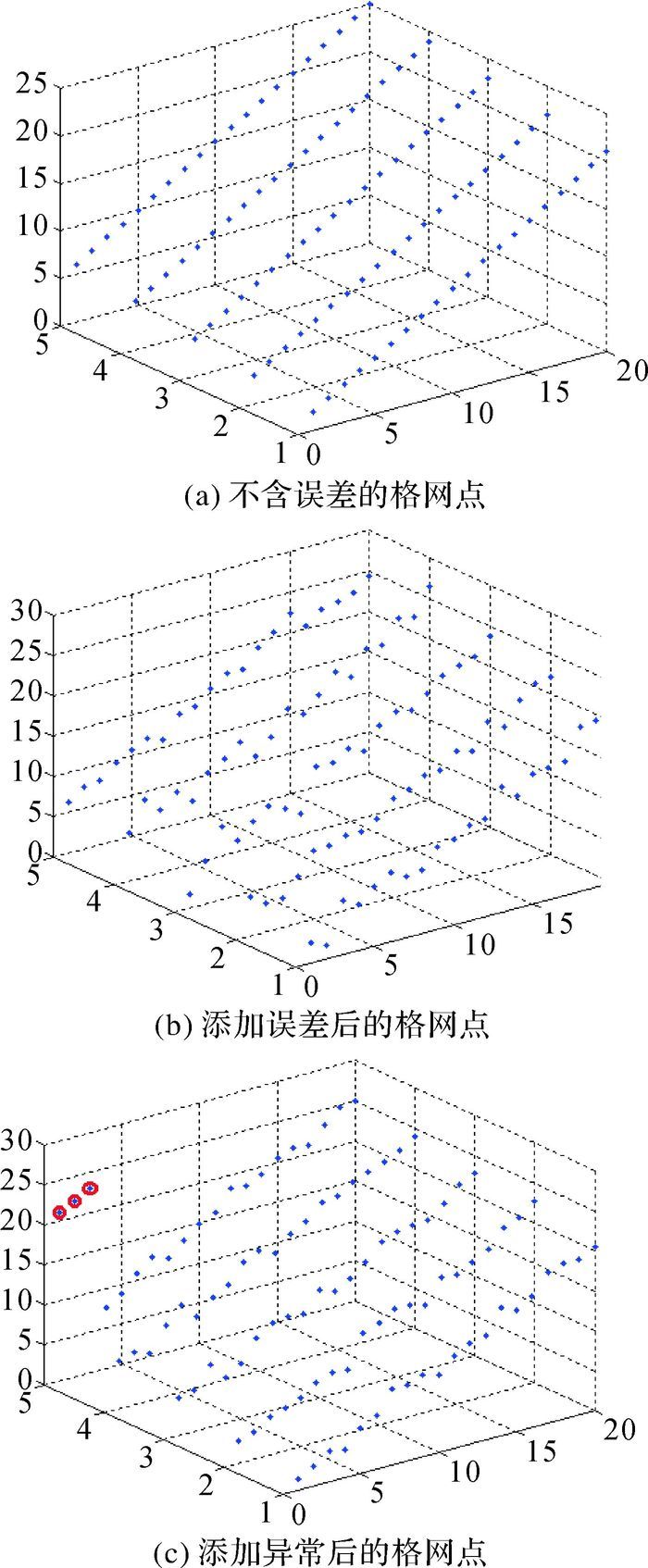
|
| 图 3 模拟格网点 |
(2) 为这组格网点的Z值添加一组服从N (0, 1) 标准正态分布的误差向量(如图 3(b)所示),将未添加误差的格网点视为DEM真值数据,添加误差的格网点视为失真DEM数据。
(3) 重复步骤(1)、(2),再添加3组不同误差向量,且格网点数量分别为500、1000、1500,形成4组数据,用LS和RANSAC对其修复。
为了比较LS与RANSAC在处理格网点出现明显异常情况下的处理能力,重复上述3个步骤重新模拟4组数据并在每组数据中添加3%的异常点(如图 3(c)所示,圆圈标注的即为异常点),用此含有异常点的模拟数据再次进行试验。
给高程Z (Z=[z1, z2, …, zn]T)添加服从N (0, 1) 正态分布的误差向量后,数据整体呈现出有规律状态,但是数据不处于同一平面,部分数值见表 1,可以模拟出DEM格网数据的分布情况。
| X | Y | 原Z值 | 添加误差后Z值 |
| 1 | 1 | 2 | 1.332 317 080 487 22 |
| 1 | 2 | 3 | 4.753 613 980 245 87 |
| 1 | 3 | 4 | 6.467 044 741 743 38 |
| 1 | 4 | 5 | 4.267 128 688 964 84 |
| 1 | 5 | 6 | 4.085 975 998 275 27 |
| 2 | 1 | 3 | 3.495 818 268 900 71 |
| 2 | 2 | 4 | 3.295 755 411 228 77 |
| 2 | 3 | 5 | 4.922 712 760 197 14 |
| 2 | 4 | 6 | 5.900 135 725 502 73 |
| 2 | 5 | 7 | 7.322 427 621 851 12 |
| 3 | 1 | 4 | 2.691 606 423 194 51 |
| 3 | 2 | 5 | 5.237 142 922 925 95 |
| 3 | 3 | 6 | 5.582 581 650 806 69 |
| 3 | 4 | 7 | 5.510 174 415 820 73 |
| 3 | 5 | 8 | 7.858 084 950 512 64 |
| 4 | 1 | 5 | 3.954 015 534 123 14 |
| 4 | 2 | 6 | 8.864 112 237 669 82 |
| 4 | 3 | 7 | 7.050 205 398 902 23 |
采用LS进行修复,试验结果如图 4、图 5所示,可以看出4组试验中采用LS修复后所得平面与真值平面之间的夹角(如图 4所示)及高程中误差(如图 5所示)都比RANSAC小。总体上看,两种算法都提高了数据精度,与真值平面的夹角和高程中误差都会随着格网点的增加而减小。
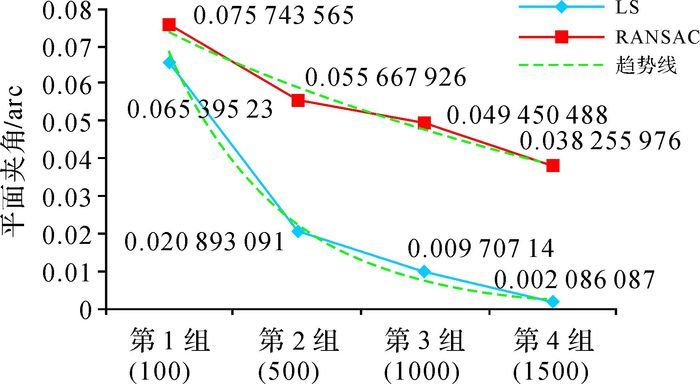
|
| 图 4 不含异常点数据修复前后的平面间夹角 |
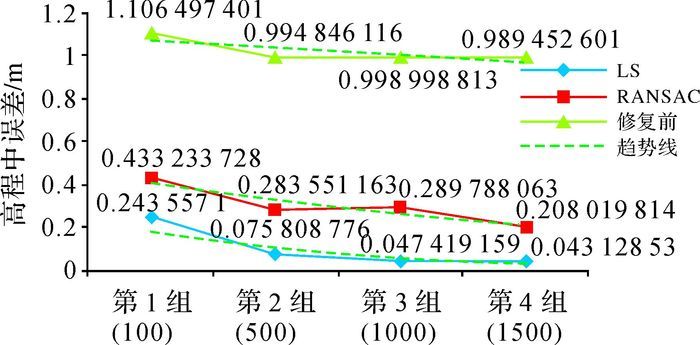
|
| 图 5 不含异常点数据修复前后的高程中误差 |
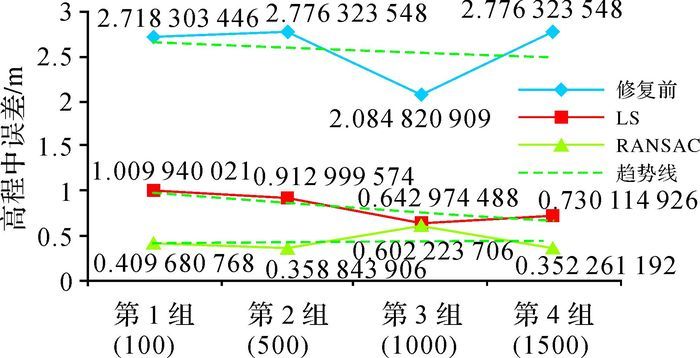
用含有异常的模拟数据进行试验,试验结果如图 6、图 7所示,可以看出每组试验中采用RANSAC进行修复,所得平面与真值平面的夹角(如图 6所示)和高程中误差(如图 7所示)都小于LS。总体上格网点数目越多修复效果越好,且修复能力越来越接近。
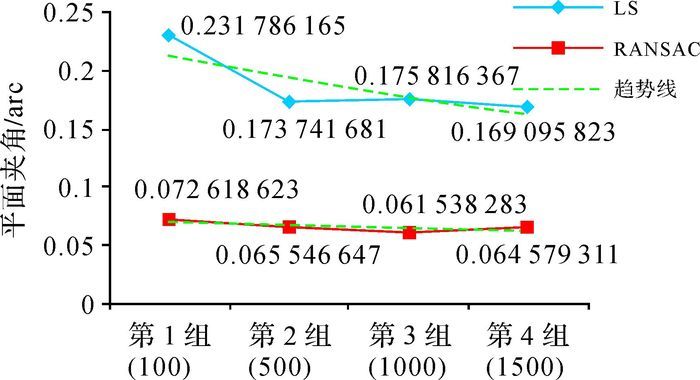
|
| 图 6 含有异常点数据修复前后的平面夹角 |
|
| 图 7 含有异常点数据修复前后的高程中误差 |
试验采用的模拟数据一方面能够避免抽样的随机性,可以模拟出不同误差的失真数据,另一方面方便对修复后所得数据进行质量检测,试验结论总结如下:
(1) 当不存在异常点时,用LS修复所得数据相比RANSAC更加贴近真值数据,但随着数据量增大,两者的修复效果越来越接近。
(2) 当存在明显异常点时,RANSAC的数据修复能力要比LS强,所得平面更接近原平面,所得数据精度也更高。这也说明RANSAC能够更好地适应高程异常情况,比LS更加稳定,鲁棒性更好。
(3) 两种算法的修复效果都随着格网点的增加越来越好,说明当存在大量格网点时两种算法都能达到很好的修复效果。
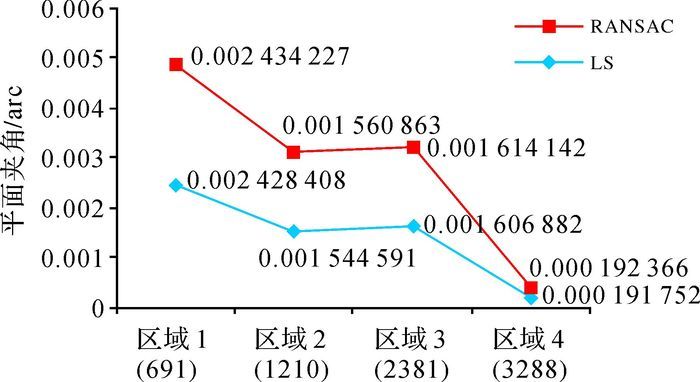
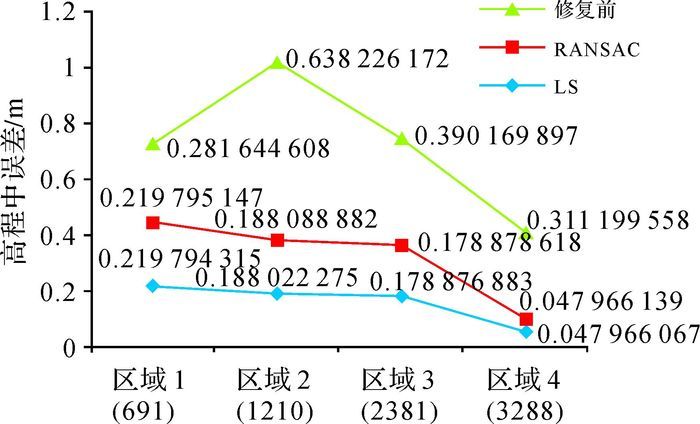
3.4 用样区规则格网DEM数据进行检验为了验证上述结论是否适用于实际采样数据,本文从1:10 000等高线地形图中随机选取了4个水库样区,并获取它们的DEM数据,由于数据的误差情况未知,在试验前对LS与RANSAC的修复效果保有未知性。样区DEM格网点数目是递进的,分别为691、1210、2381、3288,由于格网点所属真实平面不可求,样区为水库,其面积远小于湖泊、河流,可视为静水状态,故本文将其视为水平面,其高程为等高线标注的值。求出修复后的数据所处平面与水平面的夹角(如图 8所示),以及修正前后DEM高程中误差(如图 9所示)结果。
|
| 图 8 采样数据修复后所得平面与水平面夹角 |
|
| 图 9 采样数据修复前后高程中误差 |
用实际采样中的失真数据进行结论验证试验后,试验结果与采用模拟试验时基本保持一致,具体可总结为如下几个方面:
(1) 当存在大量格网点时,采用LS与RANSAC进行失真修复所得平面与水平面之间的夹角精度可达0.001 arc (如区域1—3) 甚至0.000 1 arc (如区域4),两种算法都能降低高程中误差的大小,修复所得DEM的高程中误差都远远小于国家标准[22]。
(2) 由于样区数目较少,且数据中不存在异常数据,从试验结果上看LS的修复效果要稍优于RANSAC。但当采样较多时,存在异常数据的样区不可避免,当存在异常数据时,根据采用模拟数据试验时RANSAC具有更好的鲁棒性,本文推荐采用RANSAC进行失真修复。
综合来看,两种算法的修复效果会随着格网点增多而变好,且修复能力会越来越接近,试验结果基本与用模拟数据时保持一致。两种算法都能够达到很好的修复效果,但与LS相比,RANSAC更能够适应异常点的干扰,具有很好的鲁棒性。
4 结语本文用地形特征约束失真DEM的形态结构,并采用了两种算法估算其真值表达式,进而展开修复工作。结果表明,采用LS与RANSAC都能达到很好的修复效果,且随着格网点数目的增多,修复效果都越来越好,但RANSAC比LS更加稳定,鲁棒性更好。
本文只是针对规则地形中的平面结构地形进行了失真修复试验,但文中的失真修复方法具有普适性,所提出的两种算法也提供了选择思路。其他规则地形如半球面状、锥面状、抛物面状地形等,都可以进行失真修复,只要确定了地形特征模型再选择相应算法,即可运用本文所提的相应技术方法达到修复效果。
| [1] | 李志林, 朱庆. 数字高程模型[M]. 武汉: 武汉大学出版社, 2000. |
| [2] | 周波. 语义约束的地形建模方法研究[D]. 南京: 南京师范大学, 2012. |
| [3] | 卢华兴. DEM误差模型研究[D]. 南京: 南京师范大学, 2008. http://www.airitilibrary.com/Publication/alDetailedMesh?DocID=6848477 |
| [4] | 吴艳兰, 胡海, 胡鹏, 等. 数字高程模型误差及其评价的问题综述[J]. 武汉大学学报(信息科学版), 2011, 36(5): 568–574. |
| [5] | AGUILAR F J, MILLS J P, DELGADO J, et al. Modeling Vertical Error in LiDAR-derived Digital Elevation Models[J]. ISPRS Journal or Photogrammetry and Remote Sensing, 2010, 65(1): 103–110. DOI:10.1016/j.isprsjprs.2009.09.003 |
| [6] | 胡鹏, 吴艳兰, 胡海. 数字高程模型精度评定的基本理论[J]. 地球信息科学, 2003, 5(3): 64–70. |
| [7] | 胡鹏, 吴艳兰, 胡海. 再论DEM精度评定的基本理论问题[J]. 地球信息科学, 2005, 7(3): 28–33. |
| [8] | HU Peng, LIU Xiaohang, HU Hai. Accuracy Assessment of Digital Elevation Models Based on Approximation Theory[J]. Photogrammetric Engineering and Remote Sensing, 2009, 75(1): 49–56. DOI:10.14358/PERS.75.1.49 |
| [9] | GUAN Yunlan, CHENG Xiaojun, SHI Guigang. A Robust Method for Fitting a Plane to Point Cloud[J]. Journal of Tongji University(Natural Science), 2008, 36(7): 981–984. |
| [10] | 赵争. 地形复杂区域InSAR高精度DEM提取方法[J]. 测绘学报, 2016, 45(11): 1385. DOI:10.11947/j.AGCS.2016.20160357 |
| [11] | 张锦明, 游雄, 万刚. DEM插值参数优选的试验研究[J]. 测绘学报, 2014(2): 178–185. |
| [12] | 王琴, 陈蜜, 刘书军, 等. 利用升降轨道SAR数据获取DEM的试验研究[J]. 测绘通报, 2015(6): 39–43. |
| [13] | 范强, 朱添翼, 李永化. DEM曲面分区内插方法研究[J]. 测绘通报, 2016(11): 64–66. |
| [14] | 王峰, 丘广新, 程效军. 改进的鲁棒迭代最小二乘平面拟合算法[J]. 同济大学学报(自然科学版), 2011, 39(9): 1350–1354. |
| [15] | 鲁铁定. 总体最小二乘平差理论及其在测绘数据处理中的应用[D]. 武汉: 武汉大学, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10486-2010167252.htm |
| [16] | 章嘉人. 语义规则约束下的DEM与二维矢量数据融合方法研究[D]. 南京: 南京师范大学, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10319-1011249503.htm |
| [17] | SCHNABEL R, WAHL R, KLEIN R. Efficient RANSAC for Point-cloud Shape Detection[J]. Computer Graphics Forum, 2007, 26(2): 214–226. DOI:10.1111/cgf.2007.26.issue-2 |
| [18] | 宋卫燕. RANSAC算法及其在遥感图像处理中的应用[D]. 华北电力大学, 2011. http://cdmd.cnki.com.cn/Article/CDMD-11412-1011107633.htm |
| [19] | ZHOU Chunlin, ZHU Hehua, LI Xiaojun. Research and Application of Robust Plane Fitting Algorithm with RANSAC[J]. Computer Engineering and Applications, 2011, 47(7): 177–179. |
| [20] | 陶本藻, 邱卫宁. 误差理论与测量平差[M]. 武汉: 武汉大学出版社, 2012. |
| [21] | 管兴胤, 李真富, 宋朝晖. 贝叶斯统计在测量数据拟合处理中的应用[J]. 核电子学与探测技术, 2010, 30(4): 503–505, 523. |
| [22] | 中华人民共和国测绘行业标准. 基础地理信息数字产品1: 100001: 50000数字线划图: CH/T 1011-2005[S]. 北京: 测绘出版社, 2005. |


