2. 精密工程与工业测量国家测绘地理 信息局重点实验室, 湖北 武汉 430079;
3. 武汉大学测绘学院, 湖北 武汉 430079
2. Laboratory of Precision Engineering and Industrial Surveying of National Administration of Surveying, Mapping and Geoinformation, Wuhan 430079, China;
3. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China
地基合成孔径雷达(ground-based synthetic aperture radar,GB-SAR)干涉测量技术是近十多年间发展起来的地面主动微波遥感形变探测技术。它主要应用宽带雷达探测技术对雷达信号辐射区域进行高分辨距离域成像,利用合成孔径雷达技术获取方位向分辨能力,并利用微波干涉测量技术对目标形变量进行提取计算[1-4]。与星载InSAR技术相比,GB-SAR结构简单,连续监测模式下没有空间基线,一般无需考虑导轨基线误差、地平相位及地形相位误差影响。在大坝、支护高边坡、危岩体和滑坡等小区域变形监测应用中,GB-SAR可以为监测目标建立特定的几何场景,并根据目标变形特征灵活确定时间基线[5-9]。
目前GB-SAR系统的合成孔径一般通过一条固定长度的导轨来实现,如意大利的IBIS-L/M系统、欧盟联合研究中心(JRC)的LISA系统及荷兰的FastSAR系统等[10-11]。雷达传感器在轨移动过程中发射与接收调制电磁波信号,采集监测目标在导轨各个采样点处及各个采样频率下的回波信号,通过后期数字信号处理实现方位向的分辨能力[12-13]。因此,导轨的空间位置直接决定了GB-SAR影像投影面和影像中轴线的位置,进而影响雷达影像二维平面坐标到地方三维坐标的投影计算。本文深入研究了GB-SAR传感器运行导轨的倾斜度对GB-SAR影像坐标变换的误差影响,对实际GB-SAR形变监测应用工作及变形信号的三维分析与解译具有参考意义。
1 GB-SAR系统成像的投影方式由于成像方法与空间几何关系上的区别,GB-SAR的坐标系统与星载SAR影像坐标系统存在较大差异。星载SAR卫星从高空俯视地表,目标区域满足雷达天线远场近似条件,经过一定处理后最终得到规则格网下的SAR影像数据[14]。GB-SAR作用距离相对较近,目标区域处于雷达天线辐射的近场区附近,一般不满足远场近似条件,形成了GB-SAR影像特殊的扇形格网坐标系。
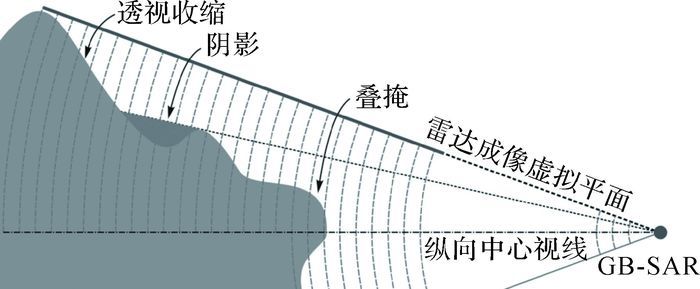
与星载SAR影像类似,在经过投影计算后,GB-SAR影像中同样存在透视收缩、雷达阴影、叠掩和顶底位移等现象,如图 1所示。GB-SAR所探测的变形是实际变形量在雷达视线向(light of sight, LOS)的投影,按照目标到雷达中心的斜距将视场空间划分为一系列的同心球。不难看出,在竖直平面内,各距离向分辨单元以雷达中心点为中心,以到雷达中心的距离为半径沿圆弧线投影到同一个平面上。实际变形值和雷达中心视线的朝向实际上并没有直接关系。因此,GB-SAR的投影面坐标系以雷达运行导轨为中心线任意转动,并不会影响雷达坐标系下的坐标数值。GB-SAR的特殊投影方式不仅决定了距离向和方位向分辨单元的划分形式,同时也决定了GB-SAR影像坐标系统变换的方法。
|
| 图 1 GB-SAR影像二维平面坐标系统的投影方式 |
GB-SAR影像二维平面坐标到地方三维坐标的转换一般需要利用外部高程数据(如测区DTM)进行[15]。在地方三维坐标系下的高程点可依据GB-SAR成像的投影原理转换计算为投影面的平面坐标,进而利用其与GB-SAR影像像元坐标的匹配关系实现逆向求解像元三维坐标,具体分为以下3个步骤。
2.1 轴系水平旋转GB-SAR的投影平面由雷达中心位置和导轨空间位置共同决定。在确定雷达中心在三维地形坐标系中的坐标之后,首先需要进行GB-SAR二维影像坐标系到三维地形坐标系的水平角度旋转。
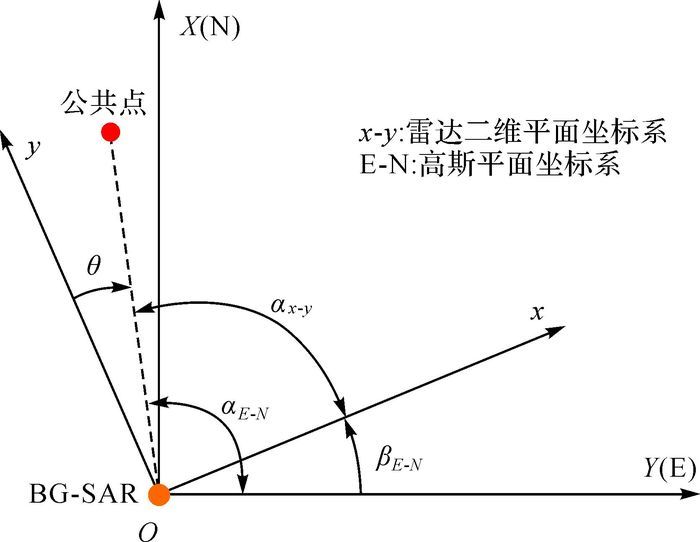
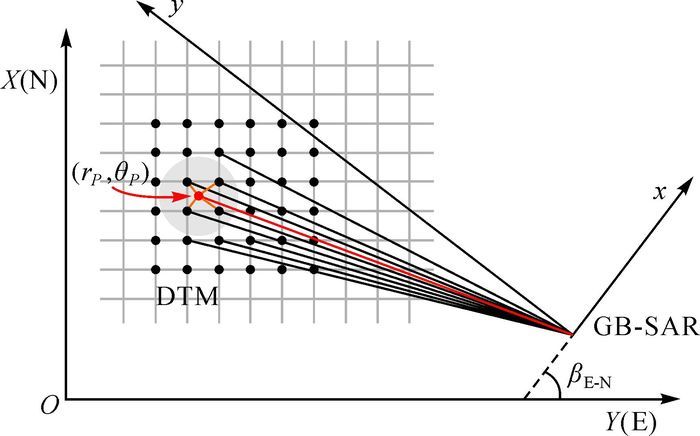
不考虑GB-SAR雷达中心平面位置的平移计算,图 2显示了GB-SAR影像平面坐标系和地方平面坐标系之间的相互关系。xOy为GB-SAR的雷达二维平面坐标系,EON为地方高斯平面坐标系。θ为雷达二维平面坐标系下目标点到雷达中心线方向的偏角。αx-y为xOy坐标系下目标点的极角,αE-N为EON坐标系下目标点的极角,而βEON为两个平面坐标系之间的夹角,即需要计算的轴系水平转角。轴系水平转角一般利用坐标系之间的公共点计算。所选公共点应同时具有两个坐标系下的坐标,并在两个坐标系中都能够清晰、准确地分辨出来。通常可以选择反射强度较高的岩体、反射强度低的阴影区域边缘点作为公共点以有利于该角度的计算。假设公共点在地方高斯平面坐标系下的坐标为(Xref,Yref)。该坐标系下雷达中心点的坐标为(Xradar,Yradar)。公共点在雷达平面坐标系下的坐标为(xref,yref),该坐标系下雷达中心点为坐标系原点,即坐标为(0,0)。分别计算公共点在两个坐标系下的偏角
|
| 图 2 坐标系轴系关系与水平角度旋转 |
 (1)
(1) 进而计算两坐标轴的水平轴系转角βE-N,该转角决定了高斯平面与雷达平面坐标系之间的旋转关系,在雷达整个连续监测过程中是不会发生改变的。
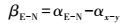 (2)
(2) 在GB-SAR影像平面坐标系下,像元由到雷达中心距离和偏离雷达中心线角度唯一确定,通过简单的极坐标计算可转换为笛卡尔直角坐标系坐标。
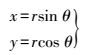 (3)
(3) 式中,r为目标点到雷达中心的距离;θ为目标点偏离雷达中心线的角度,且左偏为负右偏为正。
GB-SAR成像过程的几何投影方式使得雷达二维平面坐标(r, θ)或(x, y)不能直接转换为基于高斯-克吕格投影得到的二维平面坐标(E, N)。为了能精确进行雷达影像坐标系统变换,需要预先知道雷达影像覆盖区域的高程信息。下面利用测区DTM数据恢复GB-SAR影像像元三维空间关系。
DTM数据通常用二维数组表示,行列分别表示东坐标E和北坐标N,各元素表示高程Z。假设雷达影像内一像元点P,其雷达平面坐标为(xP, yP),相应地表三维坐标系坐标为(EP, NP, ZP)。P点的雷达平面坐标(xP, yP)也可以表示为极坐标形式
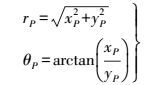 (4)
(4) 像元三维空间关系的恢复实际上就是求取雷达影像中的P点在DTM中的对应点。为了达到上述目的,通常先将DTM数据按照式(5) 转化为二维平面上的极坐标形式,从而可以将DTM数据的极坐标数据与雷达像元的极坐标直接进行匹配,这一过程可以称为三维地形坐标的极坐标化
 (5)
(5) 式中,(E, N, Z)为DTM数据;(Eradar, Nradar, Zradar)为雷达中心在DTM三维坐标系下的坐标;βE-N为轴系水平转角。
2.3 GB-SAR成像投影面上像元与地形点的邻近匹配对DTM高程数据极坐标转化后,在其数据中寻找与P (rP, θP)最为接近的点,并将该点的三维坐标作为像元点P (xP, yP)对应的三维空间坐标系下的坐标,如图 3所示。对于规则格网下的三维DTM数据,在完成极坐标化后,通常给定一定的区间范围按照行列号进行搜索。分别使格网点的斜距与极角与目标像元极坐标的差值最小,将该格网点的三维坐标作为像元的三维坐标。按照同样的方法对雷达影像中有效像元进行计算,至此便基本完成了雷达二维影像像元三维信息的恢复工作。
|
| 图 3 DTM的极坐标化与雷达像元的三维恢复 |
上述分析默认假设雷达传感器运行导轨水平,雷达中心线在水平面内。而实际这种理想情况是很难达到的,雷达导轨不可避免会有侧倾角和俯仰角。水平转角的误差只能在转角计算时增加多余控制条件予以削弱,而侧倾角、俯仰角可以通过一定的补偿方法进行计算补偿。下面分析侧倾角和俯仰角对外部高程数据极坐标化投影误差的形成机理。
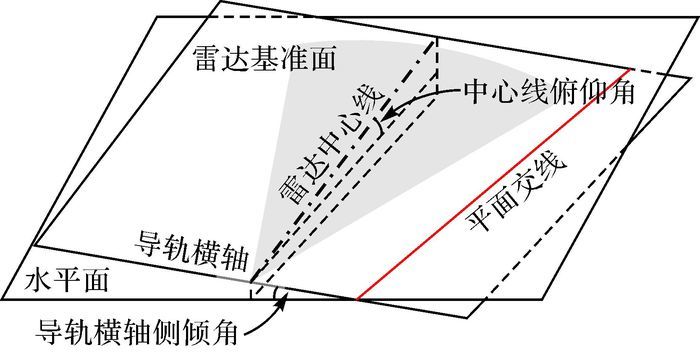
GB-SAR聚焦影像的最终形成主要由3个几何要素决定。第一是雷达中心的空间位置,该位置限定了雷达所能辐射的地表区域范围。第二是雷达导轨横轴的姿态,该轴线经过雷达中心且平行于雷达传感器滑行导轨。导轨横轴的水平角初步限定了雷达视场的基本朝向。第三是雷达中心线,该轴线是雷达辐射信号的中心轴线,经过雷达中心且垂直于导轨横轴。雷达中心线最终决定了GB-SAR影像的成像中心位置。导轨横轴的侧倾角与雷达中心线共同决定了一个虚拟的雷达基准面,这一平面是雷达坐标系统形成和计算的基准,如图 4所示。我们知道雷达天线辐射信号在横向和纵向上均具有一定波束角,因此在雷达中心位置和雷达基准面确定后即可确定雷达成像的最优辐射区域。
|
| 图 4 雷达基准面与GB-SAR成像的几何要素 |
GB-SAR系统导轨的安装直接确定了雷达传感器运行的姿态,即确定了雷达导轨横轴与雷达中心线朝向,从而为雷达影像的形成提供了一个固定的投影基准平面。实际上,GB-SAR导轨的安装并不能保证雷达基准面与水平面的完全重合。而笔者在对DTM数据或其他高程数据进行极坐标化时是以水平面为参考面的。因此有必要对导轨倾角对三维地形坐标极坐标化的误差影响进行分析和讨论。
3.1 雷达中心线俯仰角对极坐标化的误差影响假设导轨横轴侧倾角为零,系统中只存在雷达中心线的俯仰角ε。外部高程数据相对于水平面进行极坐标化处理,进而与以雷达参考面为基准的雷达平面极坐标进行比较计算。无论以哪一个平面作为参考面,目标到雷达中心的斜距r均不会发生变化。但基准面的选择直接影响了投影点到雷达中心线的偏角θ,从而使得极坐标化的坐标值发生偏离。
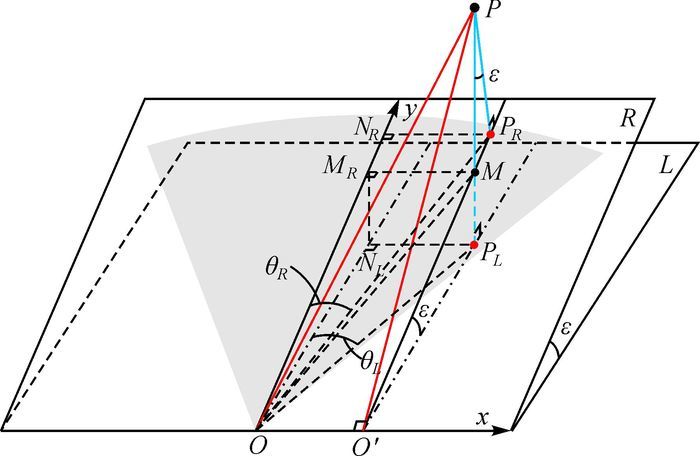
图 5说明了雷达中心线俯仰角对极坐标化的影响。平面L和R分别为水平面和雷达基准面,假设系统不存在导轨横轴侧倾角影响,雷达中心线俯仰角为ε。R为GB-SAR系统成像实际的参考面,而L则是外部高程数据的参考面。监测区域某一点P在雷达影像上的对应点是该点到平面R垂线的垂足PR,而在实际高斯坐标系统中的对应点是该点到水平面L垂线的垂足PL,该垂线与平面R相交于M点。MMR和PRNR分别垂直于雷达中心线。从图中易知,∠PLONL是点P以水平面L为基准面的中心线偏角θL,∠PRONR是点P以雷达基准面R为基准的中心线偏角θR。基准面的选择使得θL和θR存在差异,从而使三维数据到平面的极坐标化产生系统性偏差。
|
| 图 5 雷达中心线俯仰角与投影点到中心线偏角的关系 |
假设目标点P到雷达中心O点的距离为r,点P到水平面的高度PPL为H,点P以水平面为基准偏离中心线的角度为θL,即
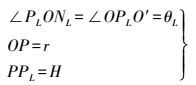 (6)
(6) 在直角三角形△OPPL中,有
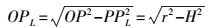 (7)
(7) 在直角三角形△OPLO′中,有
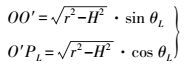 (8)
(8) 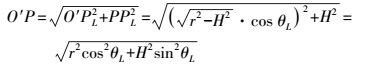 (9)
(9) 在直角三角形△O′PPL中
 (10)
(10) 考虑到∠PO′PR=∠PO′PL-ε,在直角三角形△O′PPR中有
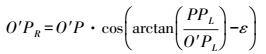 (11)
(11) 进而在直角三角形△OO′PR中可以求得
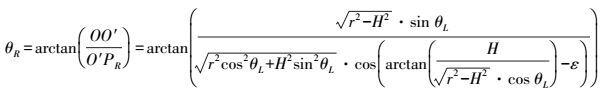 (12)
(12) 式中,雷达中心线上仰时ε为正值,下俯时为负。
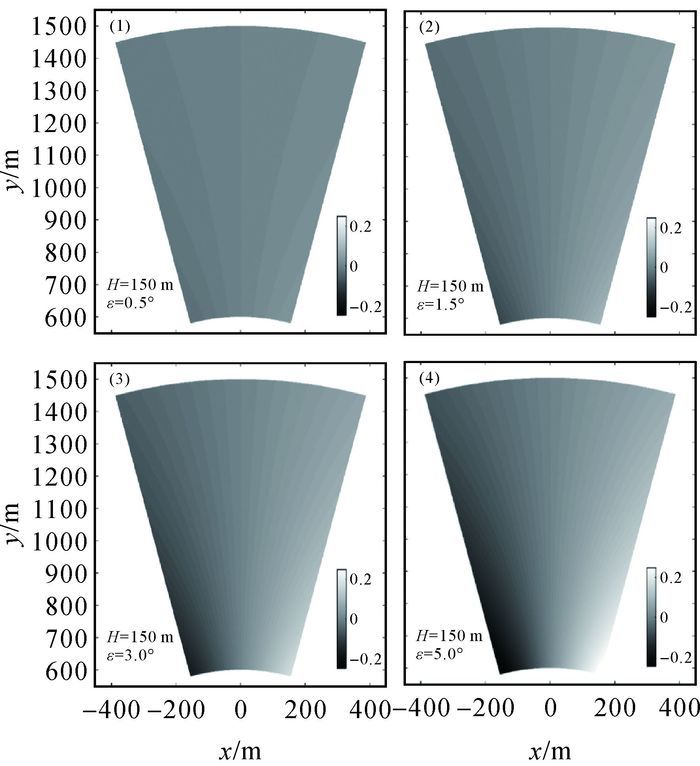
令r=600~1500 m,θL=-15°~15°,H=150 m,计算俯仰角ε分别为0.5°、1.5°、3.0°和5.0°时两极偏角的差值Δθ=θL-θR。计算结果表明,三维地形坐标的极坐标化使得各像元点相对于雷达中心线向两侧偏移,但偏移的角度非常小。如图 6所示,逆时针偏移为正,反之为负。ε=0.4°时,平均角度偏移量幅值为0.019°,最大值也仅为0.065°。实际上在导轨安装定位时,中心线俯仰角ε的0.2°控制精度是完全可以达到的。而IBIS-L系统的方位向分辨率为4.4 mrad=0.252 1°,相比于该分辨率的大小,导轨安装定位时产生的俯仰角ε可以忽略不计。
|
| 图 6 雷达中心线俯仰角对极偏角影响的模拟计算 |
现在考虑系统中只存在雷达导轨侧倾角ω的情况。通常情况下导轨横轴的侧倾可以看作导轨绕雷达中心线发生的旋转变化。无论以哪一个平面作为参考面,目标到雷达中心的斜距r均不会发生变化。
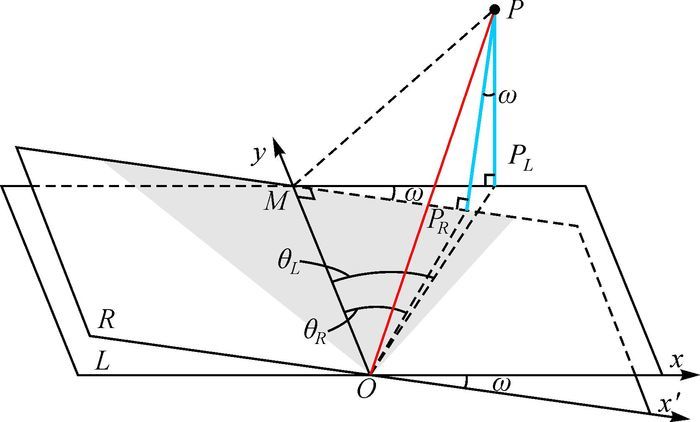
图 7说明了雷达导轨横轴侧倾角对极坐标化的影响。平面L和R分别为水平面和雷达基准面,现假设系统中不存在雷达中心线俯仰角的影响,雷达导轨横轴侧倾角为ω。点P在雷达影像上的对应点是该点到平面R垂线的垂足PR,而在实际高斯坐标系统中的对应点是该点到水平面L垂线的垂足PL。∠PLOM是点P以水平面L为基准面的中心线偏角θL,∠PROM是点P以雷达基准面R为基准的中心线偏角θR。
|
| 图 7 雷达导轨侧倾角与投影点到中心线偏角的关系 |
假设目标点P到雷达中心O点的距离为r,点P到水平面的高度PPL为H,点P以水平面为基准偏离中心线的角度为θL,即
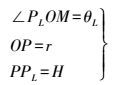 (13)
(13) 在直角三角形△OPPL中,有
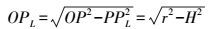 (14)
(14) 在直角三角形△OPLM中,有
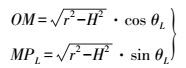 (15)
(15) 因此,有
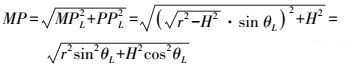 (16)
(16) 在直角三角形△MPPL中
 (17)
(17) 考虑到∠PMPR=∠PMPL+ω,在直角三角形△MPPR中有
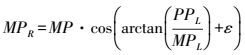 (18)
(18) 进而在直角三角形△OMPR中可以求得θR
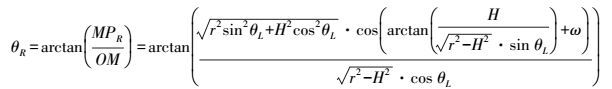 (19)
(19) 雷达导轨横轴逆时针侧倾ω为正,反之为负。
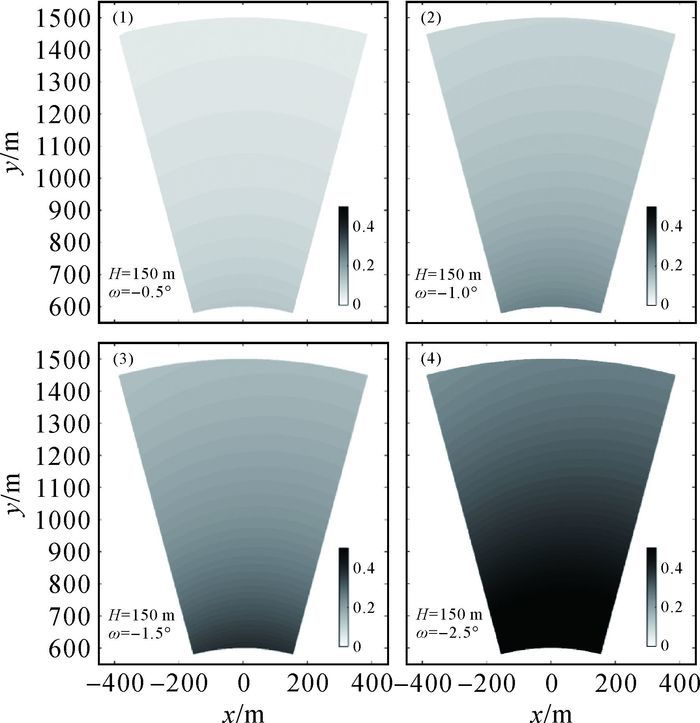
令r=600~1500 m,θL=-15°~15°,H=150 m,计算俯仰角ω分别为-0.5°、-1.0°、-1.5°和-2.5°时两极偏角的差值Δθ=θL-θR。俯仰角ω越大,其对极偏角的影响越大,俯仰角ω在-1.0°时,其产生的极坐标化误差最大值已经达到1个方位向分辨单元。ω极坐标化误差不是关于y轴对称的,而且ω值越大这种不对称性越明显。相比于雷达中心线俯仰角,极坐标化误差对雷达导轨横轴的侧倾角更为敏感,在实际监测中导轨的横向平整度需做严格控制。
由于雷达中心线俯仰角对极坐标化误差的影响较小,在考虑导轨姿态的综合性影响时,一般只需考虑雷达导轨侧倾角ω的影响。实际监测中,需要利用精度较高的管水准器测量雷达导轨侧倾角和中心线俯仰角,用于控制导轨的安装与定位。通常情况下容易获得0.2°以内的测量精度。横轴侧倾角引起的极坐标化误差补偿在水平转角计算完成之后进行。此时,三维坐标已从高斯坐标系转入局部三维坐标系O-xlocalylocalzlocal。该局部三维坐标系以雷达中心为原点,以雷达中心线为ylocal轴(由于误差允许,可以认为ylocal轴平行于水平面)。xlocal轴过原点,垂直于ylocal轴,并且平行于水平面。该坐标系下,各三维坐标点到原点即雷达中心的距离(r)、与雷达中心的相对高度(H)及以水平面为基准相对于雷达中心线的偏角(θL)都可以得到。因此可以计算各点相应的角度差值,作为偏角改正值改正原偏角值,即可完成横轴侧倾角引起的极坐标化误差补偿,如图 8所示。
|
| 图 8 雷达导轨横轴侧倾角对极偏角影响的模拟计算 |
GB-SAR运行导轨的空间姿态直接影响雷达中心线的朝向及成像投影面的空间方位,进而决定了二维平面坐标系统坐标轴的方位。本文揭示了导轨姿态倾角引起的影像坐标投影变换误差的分布规律。研究结果表明,导轨安装定位时俯仰角产生的偏角误差由中心线向两侧逐渐增加,雷达中心线两侧偏角误差呈现反号对称;数值较小,通常可忽略不计。极坐标化误差对雷达导轨横轴的侧倾角更为敏感,所引起的偏角误差与高度角相关,等距离处的偏角误差相差不大,在实际监测应用中导轨的横向平整度需严格控制。
| [1] | PIERACCINI M, FRATINI M, PARRINI F, et al. High-speed CW Step-frequency Coherent Radar for Dynamic Monitoring of Civil Engineering Structures[J]. Electronics Letters, 2004, 40(14): 907–908. DOI:10.1049/el:20040549 |
| [2] | 徐亚明, 王鹏, 周校, 等. 地基干涉雷达IBIS-S桥梁动态形变监测研究[J]. 武汉大学学报(信息科学版), 2013, 38(7): 845–849. |
| [3] | 王鹏, 徐亚明, 徐进军, 等. 地基干涉雷达变形监测信号静杂波去除方法研究[J]. 测绘通报, 2014(10): 15–18. |
| [4] | RÖDELSPERGER S. Real-time Processing of Ground Based Synthetic Aperture Radar(GB-SAR)Measurements[D].[S.l.]:Technische Universität Darmstadt, 2011. |
| [5] | 邹进贵, 李琴, 朱勇超, 等. 时序地基SAR子影像集监测地震滑坡灾害研究[J]. 测绘通报, 2015(S0): 152–156. |
| [6] | 黄其欢, 岳建平, 贡建兵. GBInSAR隔河岩大坝变形监测试验[J]. 水利水电科技进展, 2016, 36(3): 47–51. DOI:10.3880/j.issn.1006-7647.2016.03.010 |
| [7] | 刘斌, 葛大庆, 张玲, 等. 地基雷达干涉测量技术在滑坡灾后稳定性评估中的应用[J]. 大地测量与地球动力学, 2016, 36(8): 674–677. |
| [8] | MARGOTTINI C, ANTIDZE N, COROMINAS J, et al. Landslide Hazard, Monitoring and Conservation Strategy for the Safeguard of Vardzia Byzantine Monastery Complex, Georgia[J]. Landslides, 2015, 12(1): 193–204. DOI:10.1007/s10346-014-0548-z |
| [9] | ATZENI C, BARLA M, PIERACCINI M, et al. Early Warning Monitoring of Natural and Engineered Slopes with Ground-based Synthetic-aperture Radar[J]. Rock Mechanics and Rock Engineering, 2015, 48(1): 235–246. DOI:10.1007/s00603-014-0554-4 |
| [10] | TARCHI D, ANTONELLO G, CASAGLI N. On the Use of Ground-based SAR Interferometry for Slope Failure Early Warning:the Cortenova Rock Slide (Italy)[J]. Landslides, 2002: 337–342. |
| [11] | RÖDELSPERGER S, META A. MetaSensing's FastGBSAR:Ground Based Radar for Deformation Monitoring[J]. Spie Remote Sensing, 2014: 9243. |
| [12] | TARCHI D, CASAGLI N, FANTI R, et al. Landslide Monitoring by Using Ground-based SAR Interferometry:An Example of Application to the Tessina Landslide in Italy[J]. Engineering Geology, 2003, 68(1): 15–30. |
| [13] | TRAGLIA F, NOLESINI T, INTRIERI E. Review of Ten Years of Volcano Deformations Recorded by the Ground-based InSAR Monitoring System at Stromboli Volcano:a Tool to Mitigate Volcano Flank Dynamics and Intense Volcanic Activity[J]. Earth-Science Reviews, 2014, 139: 317–335. DOI:10.1016/j.earscirev.2014.09.011 |
| [14] | 张永红, 吴宏安, 孙广通. 时间序列InSAR技术中的形变模型研究[J]. 测绘学报, 2012, 41(6): 864–869. |
| [15] | VAZQUEZ M. Snow Cover Monitoring Techniques with GB-SAR[D].[S.l.]:Universitat Politècnica de Catalunya, 2008. |


