大地水准面的确定目前仍基于求解经典大地测量边值问题,最具有代表性的是Stokes理论和Molodesnky理论。为保证大地水准面外部扰动位为谐函数,Stokes理论要求大地水准面外部无质量。将大地水准面外部的地形质量移去,再以一定的方式对移去的地形质量进行补偿,是解算Stokes边值问题处理地形影响的基本方法。然而,无论用何种方式移去地形质量都将使大地水准面发生变化,产生间接影响。
Molodensky级数不必考虑地球质量的影响,无需作与地球密度相关的各种改正,它摆脱了Stokes方法需要已知地形密度分布的困难。但事实上地面及其外部扰动位又必然因地形起伏而变,因此其导出的级数解包含了地形影响项Gn(n=1,2,…)。计算Gn过于复杂耗时,其级数各项正负相间,收敛性目前也尚无定论,这就大大降低了Molodensky级数的实用效果。
近年来,发展了一种新型大地边值问题,即Stokes-Helmert边值问题,即在Stokes理论和计算模型的基础上,结合Helmert地形处理模式,同时兼容Molodensky理论,解算大地水准面外部扰动位的边值问题,又称Stokes双边值问题。Vaníček等于1995年介绍了Stokes-Helmert边值问题的基本原理。Sjöberg于2000年讨论了利用Stokes-Helmert法计算大地水准面过程中的地形影响,指出经典Stokes-Helmert算法已不能满足厘米级大地水准面精度的要求。Nahavandchi于2000年推导了基于Stokes-Helmert法计算大地水准面过程中直接地形影响的计算公式。罗志才于2003年比较了利用经典Stokes-Helmert方法与Sjöberg方法计算地形对大地水准面的影响,指出经典Stokes-Helmert方法存在明显的偏差,应采用更加严密的计算方法和模型。
利用Stokes-Helmert边值问题精化似大地水准面对地形影响处理技术提出了更高要求。目前大地水准面计算中地形影响的计算通常将参考面近似为平面,所有数据处理问题都可以在直角坐标系中进行理论推导和计算。然而,对于大区域乃至全球性的尺度问题,需要利用球坐标进行表达与处理,此时建立在直角坐标系中的数据处理方法已不再适用。因此,本文在已有工作的基础上,推导球坐标的Stokes-Helmert公式和严密地形影响计算公式,实现临沂厘米级大地水准面精化。首先基于确定地球外部扰动重力场的经典理论,借鉴国内外精密确定地表及其外部扰动引力位的严密解算理论,给出Stokes-Helmert边值问题的定义及Helmert重力场概念;然后根据实际算例,精确计算第2类Helmert凝聚法中由地形和凝聚层质量所产生的直接影响,以及地形及相应引力变化的间接影响,构建临沂高精度的似大地水准面模型。
1 Stokes-Helmert边值问题基本原理Helmert重力场中的Stokes边值问题可表示为
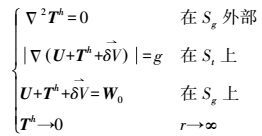 (1)
(1) 式中,St和Sg分别表示地球自然表面和大地水准面;▽为梯度算子,▽2=Δ为Laplace二阶梯度算子;U为正常位,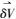
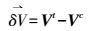 (2)
(2) 在式(1) 中, 式(2) 是一个非线性边界条件,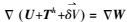
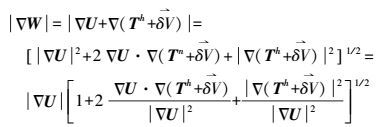 (3)
(3) 式中,g为向量的纯量积,将式(3) 中的第3项略去,作泰勒级数展开,保留线性项,则有
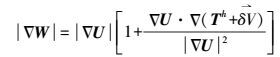 (4)
(4) 略去二阶和高阶项,取球近似,略去地球扁率,并近似取γ与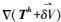
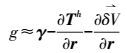 (5)
(5) 式(6) 在Sg外部成立,用于St上的P点有
 (6)
(6) 式中,r为地心距离,δA为对重力的直接地形影响。设点Q为点P沿正常重力线在正常椭球面Se上的对应点,则γP可表示为
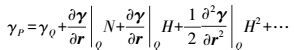 (7)
(7) 式中,N表示大地水准面高;H表示地形高,略去H3等高次项。引进空间改正,令
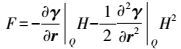 (8)
(8) 则式(7) 可写为
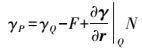 (9)
(9) 顾及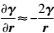
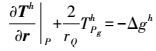 (10)
(10) 式中
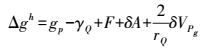 (11)
(11) Δgh称为Helmert重力异常。点P和点Q分别为地面和正常椭球面上的点,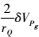
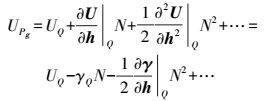 (12)
(12) 式中,∂/∂h是沿正常重力线方向的导数;N为大地水准面高;∂γ/∂h近似为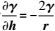
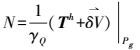 (13)
(13) 式(13) 为Helmert重力场的布隆斯公式,其中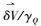
移去大地水准面外部地形质量的影响称为地形的直接影响。计算直接影响的经典公式为
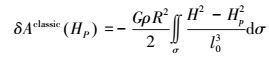 (14)
(14) 式中,G为重力常数;ρ为地壳密度;l0=2rsin ψ/2;Hp和H分别为地面点P和流动点的正常高,R=r。从严格意义上来讲,式(15) 只适用于远区积分,即l0≥H。Sjöberg于1995年将直接影响球谐展开至H2,Nahavandchi等1998年将其扩展到H3,Sjöberg于2000年将直接影响写成曲面积分模式。
对于大区域的乃至全球尺度问题,发展椭球坐标系内高精度的地形改正方法尤其重要。本文基于国际通用的GRS80椭球采用Tesseroid单元体引力效应计算地形改正的方法。对于以地心为圆心,高度H=0、H=h1的两个球面,其半径可近似表示为:r1=Rradii+0,r2=Rradii+h1,Rradii表示所选等质圆的半径(这里选地球的平均半径)。则球面扇形柱体的重力位可表示为
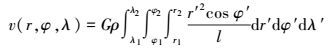 (15)
(15) 式中,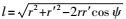
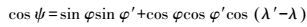 (16)
(16) 由于椭球积分困难,扇形柱体的重力位不能解析计算,但是可通过数值计算得到近似解,式(15) 可以进行级数展开。
2.2 间接地形影响恢复地形质量带来的影响称为间接影响,计算间接影响的经典计算公式为
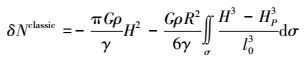 (17)
(17) 式(17) 右端第一项称为主项,第二项称为次项。Sjöberg于1995年将间接影响球谐展开至H2,Nahavandchi等于1998年将其扩展到H3。然而由于公式需要对整个地球进行积分,这在计算中是不实际的。这里将给出间接改正的严密球近似公式。假设任意一点P的地形引力可写为
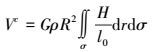 (18)
(18) 式中,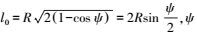
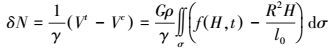 (19)
(19) 式(19) 核函数f (H, t)可表示为
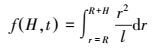 (20)
(20) 式中,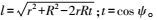
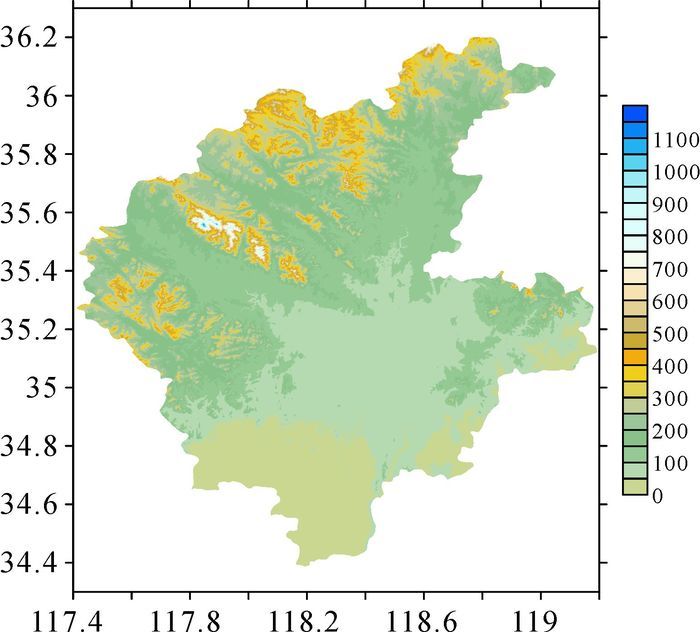
本文研究区域范围为34.3°N—36.3°N, 117.4°E—119.2°E,地形数据采用SRTM3模型。图 1为所用的SRTM3地形数据等值线图,高程最大值为1125 m,平均高程为151.7 m。
|
| 图 1 SRTM3地形数据 |
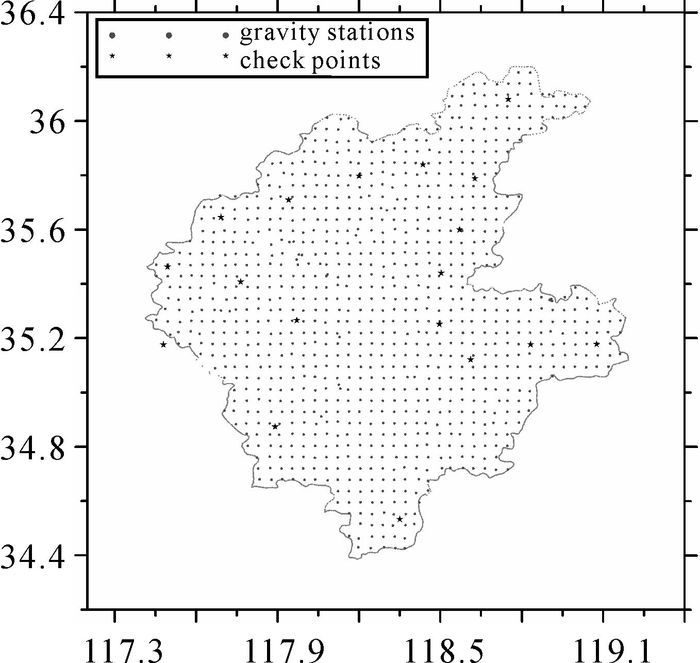
临沂市境内相对重力数据为995个,其点位分布如图 2圆点所示。为了检验地面重力数据的精度,采用该区18个长期观测的绝对重力观测数据(其点位分布如图 2中星号点所示)对相对重力测量数据进行检核。经分析,测区相对重力测量数据标准差为0.02 mGal。
|
| 图 2 地面重力测量点位分布 |
目前应用最为广泛的全球地球重力场模型是EGM2008地球重力位系数模型。利用位系数计算参考重力场的公式为
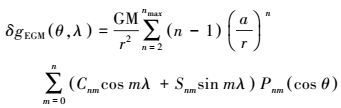 (21)
(21) 式中,Cnm、Snm为完全规格化重力位系数;GM为地心引力常数;a为参考椭球长半径;Pnmcos θ为完全规格化缔合Legendre函数;nmax为重力场模型的最大阶数2190阶。为了验证EGM2008模型在临沂地区的精度,本文采用实测地面重力数据对EGM2008模型进行外部测试。考虑到地面重力测量成果使用无潮汐基准, 模型重力场计算时也采用无潮汐基准模型。经过分析,模型数据与实测空间重力网格数据的标准差为5.66 mGal。
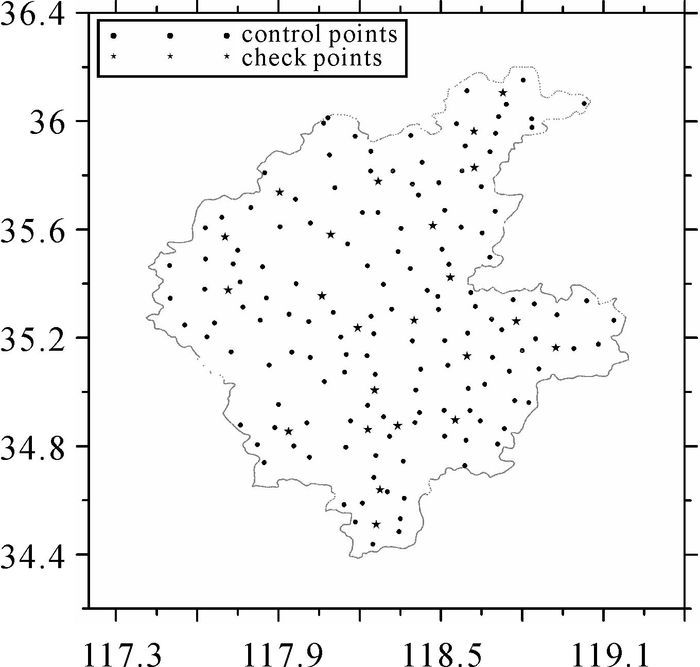
本区共有165个GPS/水准点,分布如图 3所示。其坐标系统采用2000国家大地坐标系,高程基准采用1985国家高程基准。任取其中142个点(圆点标记)作为高一级的控制点计算大地水准面,其余23个点(星号点标记)作为外部检验点,以检验求得的大地水准面的精度。
|
| 图 3 GPS/水准点分布 |
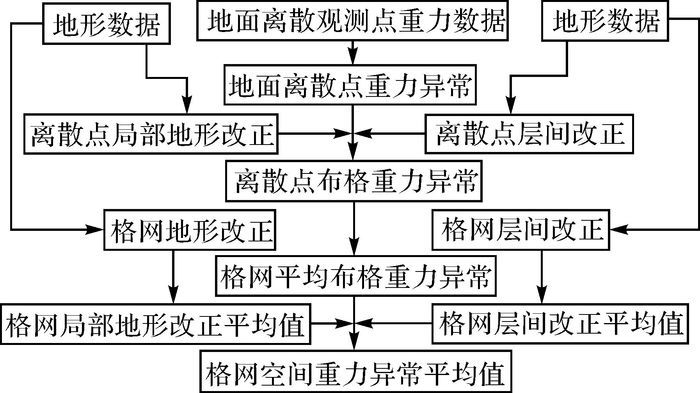
重力测量的结果是一些分布不规则的离散点重力值。为了便于使用快速傅里叶变换(FFT)等科学计算方法,离散重力数据需要进行格网化。然而由于空间重力异常的变化较大,直接对空间重力异常进行格网化将产生较大的误差,因此,通常在进行格网化之前对重力异常进行归算。本文重力归算采用布格重力异常进行格网化,具体计算步骤如图 4所示。
|
| 图 4 重力异常数据格网化计算流程 |
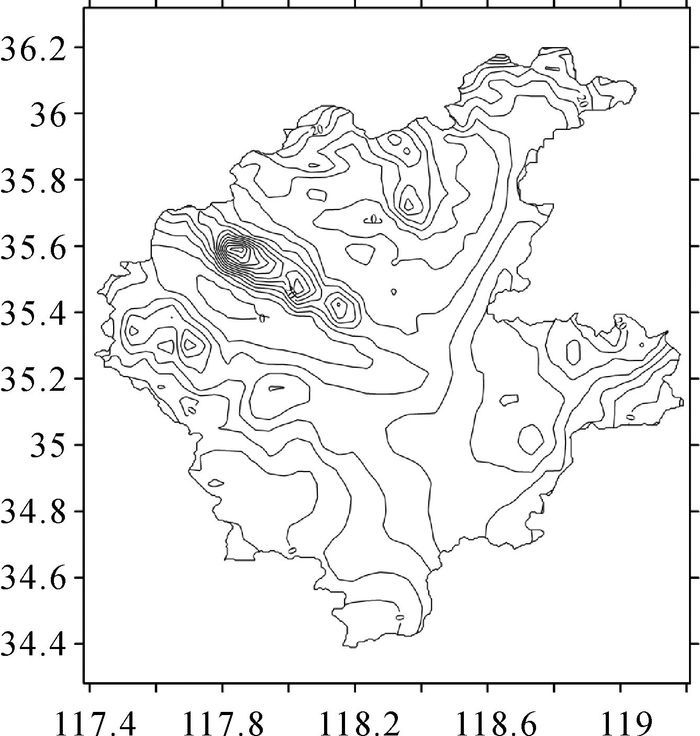
采用上述格网化步骤对地面离散数据进行格网化,格网化范围为34.3°N—36.3°N, 117.4°E—119.2°E。临沂市境内采用地面观测得到的空间异常,临沂市外空白区域采用EGM2008模型重力异常进行填充。格网化过程中的地形数据采用SRTM3模型。按图 4所述的方法,将离散重力数据格网化成2.5′×2.5′分辨率的网格点。图 5给出了格网化后的空间异常等值线图,其最大值为50.74 mGal,最小值为-6.61 mGal,平均值为9.36 mGal。
|
| 图 5 格网化后的地面空间异常 |
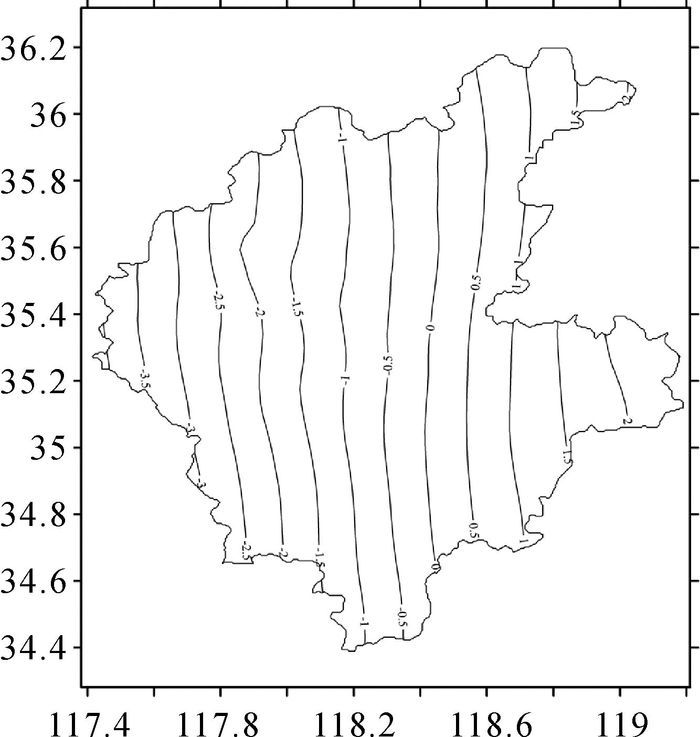
采用2.5′×2.5′格网空间重力异常作为输入数据,以EGM2008作为参考重力场,再利用第2类Helmert凝聚法计算大地水准面中的各类地形位及地形引力的影响,即牛顿地形质量引力位和凝聚层位间的残差地形位的间接影响,以及Helmert重力异常由地形质量引力位和凝聚层位所产生的引力影响。图 6给出了由Stokes-Helmert法计算的重力似大地水准面,单位为m。
|
| 图 6 临沂市重力似大地水准面等值线 |
为了评定重力似大地水准面的精度,采用171个GPS/水准资料与其进行比较。结果表明,重力似大地水准面与GPS/水准高程异常比较,差值最大值为11.43 cm,标准差为4.52 cm。同样,采用171个GPS/水准资料与EGM2008模型计算的大地水准面高进行比较,差值最大为21.04 cm,标准差为6.67 cm。由结果可见,由Stokes-Helmert方法计算的重力似大地水准面比模型结果相比,精度有显著提高。
4.2 GPS水准数据与重力似大地水准面高拟合利用高精度GPS/水准数据对上述建立的重力似大地水准面进行控制拟合,求得最终的大地水准面模型。由GPS水准测量得到的高程异常及重力似大地水准面起伏之间的拟合模型通常可表达为
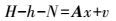 (21)
(21) 式中,H为GPS测量的大地测高;h为水准测量得到的正常高;N为重力似大地水准面起伏;x为基准不一致的拟合参数;A为系数矩阵,取决于拟合模型。本文计算中拟合模型Ax选用多面函数拟合模型,其高程异常函数可表示为
 (22)
(22) 式中,αi为待定系数;Q (x, y;xi, yi)为核函数;(x, y)为未测点坐标;(xi, yi)为已测点坐标。核函数一般可取
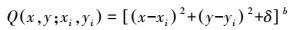 (23)
(23) 式中,δ称为平滑因子,为了得到较好的逼近效果,应作一定的试算后确定,一般可取作0;b为一个可供选择的非零实数,一般取1/2,即核函数为正双曲形。
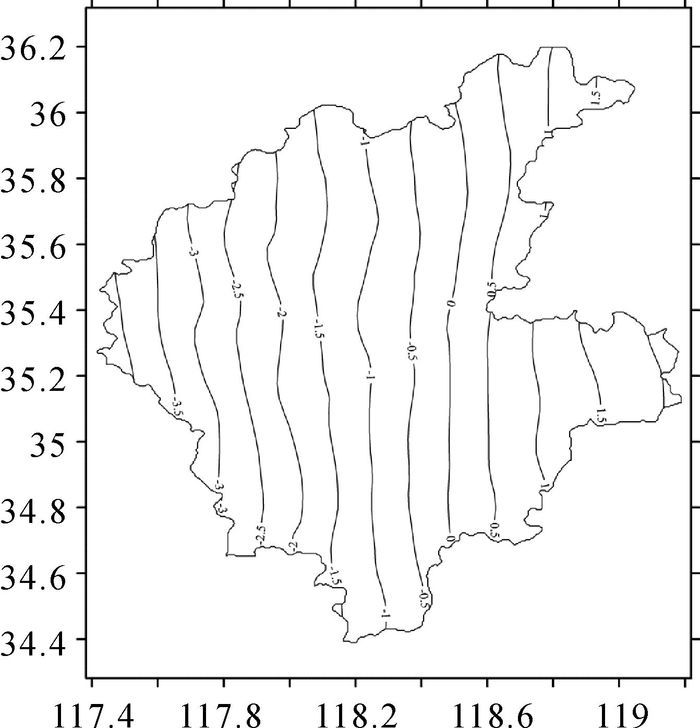
本文采用的GPS/水准点共165个。任意选取142个均匀分布的GPS水准点作为控制点,其他23个点作为检验点。控制点和检核点的点位分布如图 3所示。采用曲面函数拟合法拟合大地水准面的外符合精度,最大值为3.18 cm,最小值为-2.79 cm,标准差为1.61 cm。如图 7所示。
|
| 图 7 临沂市似大地水准面模型 |
本文从讨论地形数据在大地水准面确定中的作用出发,分析比较了Stokes和Molodensky两种经典方法处理地形影响存在的问题,给出了Stokes-Helmert边值问题的定义及数学描述,以及地形直接影响、间接影响的理论表达式,介绍了解算Stokes-Helmert边值问题的详细步骤和流程。
以格网化后的重力场模型为基础,采用Stokes-Helmert边值问题,建立临沂地区2.5′×2.5′分辨率的重力似大地水准面模型。利用GPS水准高程异常对重力似大地水准面模型进行控制拟合,求得最终的大地水准面模型。经检核点检验可知,拟合外符合精度达到1.6 cm。
| [1] | HECK B, SEITZ K. A Comparison of the Tesseroid, Prism and Point-mass Approaches for Mass Reductions in Gravity Field Modeling[J]. Journal of Geodesy, 2007, 81(2): 121–136. DOI:10.1007/s00190-006-0094-0 |
| [2] | HEISKANEN W A, MORITZ H. Physical Geodesy[M]. San Francisco: Freeman WH, 1967. |
| [3] | MARTINEC Z, VANÍČEK P. Direct Topographical Effect of Helmert's Condensation for a Spherical Approximation of the Geoid[J]. Manuscr geod, 1994, 19: 257–268. |
| [4] | NAHAVANDCHI H. On Some Methods of Downward Continua-tion of Mean Free-air Gravity Anomaly[J]. IGES Bull, 1998(8): 1–17. |
| [5] | NAHAVANDCHI H, SJÖBERG L E. Terrain Corrections to Power 3 in Gravietric Geoid Determination[J]. Journal of Geodesy, 1998, 72(3): 124–135. DOI:10.1007/s001900050154 |
| [6] | NAHAVANDCHI H. The Direct Topographical Correction in Gravimetric Geoid Determination by the Stokes-Helmert Method[J]. Journal of Geodesy, 2000, 74(6): 488–496. DOI:10.1007/s001900000110 |
| [7] | OMANG O C D, FORSBERG R. How to Handle Topography in Practical Geoid Determination:Three Examples[J]. Lournal of Geodesy, 2000, 74: 458–466. DOI:10.1007/s001900000107 |
| [8] | SJÖBERG L E. On the Quasi-geoid to Geoid Separation[J]. Manuscr Geod, 1995, 20: 182–192. |
| [9] | SJÖBERG L E. Topographic Effects by the Stokes-Helmert Method of Geoid and Quasi-geoid Determinations[J]. Journal of Geodesy, 2000, 74(2): 255–268. DOI:10.1007/s001900050284 |
| [10] | VANÍČEK P, NAJAFI M, MARTINEC Z, et al. Higher Order Reference Field in the Generalized Stokes-Helmert Scheme for Geoid Computation[J]. Journal of Geodesy, 1995, 70(3): 176–182. DOI:10.1007/BF00943693 |
| [11] | WICHIENCHAROEN C. The Indirect Effects on the Computation of Geoid Undulations[M]. Columbus: The Ohio State University, 1982. |
| [12] | VANÍČEK P, KINGDON R, KUHN M, et al. Testing Stokes-Helmert Geoid Model Computation on a Synthetic Gravity Field:Experiences and Shortcomings[J]. Studia eophysica et Geodaetica, 2013, 57(3): 369–400. DOI:10.1007/s11200-012-0270-z |
| [13] | VANÍČEK P, KLEUSBERG A. The Canadian Geoid-Stokesian Approach[J]. Manuscr Geodesy, 1987, 12(2): 86–98. |
| [14] | 郭东美, 鲍李峰, 许厚泽. 中国大陆厘米级大地水准面的地形影响分析[J]. 武汉大学学报(信息科学版), 2016, 41(3): 342–348. |
| [15] | 李建成, 陈俊勇, 宁津生, 等. 地球重力场逼近理论与中国2000年似大地水准面的确定[M]. 武汉: 武汉大学出版社, 2003. |
| [16] | 罗志才, 陈永奇, 宁津生. 地形对确定高精度局部大地水准面的影响[J]. 武汉大学学报(信息科学版), 2003, 28(3): 340–344. |
| [17] | 许厚泽. 我国精化大地水准面工作中若干问题的讨论[J]. 地理空间信息, 2006, 5(4): 1–3. |
| [18] | 章传银, 晁定波, 丁剑, 等. 厘米级高程异常地形影响的算法及特征分析[J]. 测绘学报, 2006, 35(4): 340–344. |


