2. 山东科技大学, 山东 青岛 266590
2. Shandong University of Science and Technology, Qingdao 266590, China
北斗导航卫星系统是我国自主研制的全球导航定位系统,是继美国的GPS、俄罗斯的GLONASS之后第3个成熟的卫星导航系统。目前该系统已经可以实现我国及其周边区域导航定位的功能。国内外的许多学者研究过北斗卫星精密轨道的确定,但基本上都是基于全球的MGEX站的数据。基于这种数据的测站大部分都在欧洲地区,在我国境内和周边分布比较少,因此卫星定位的几何构型不佳。GEO卫星基本是在亚洲上空,由于MGEX站的测站的分布导致GEO卫星的星下点较少,从而导致定轨精度不高。国家基准站的建立使我国能够接收北斗数据的测站大大增加,但它对北斗卫星精密定轨精度的影响还没有人作出分析。
本文主要是研究基于国家基准站的北斗数据,利用多源融合技术计算北斗卫星导航系统的精密轨道结果,并与国际上GFZ的分析中心发布的GBM精密星历进行比对,比较北斗精密轨道的精度并作详细的分析。分别计算加入国家基准站与不加入国家基准站的北斗轨道结果,得知加入国家基准站后轨道重复弧段的精度明显地要比只考虑国际站的计算结果要更优。为以后北斗卫星的观测站的布设提供指导性的意义,以提高我国北斗卫星的定轨精度。
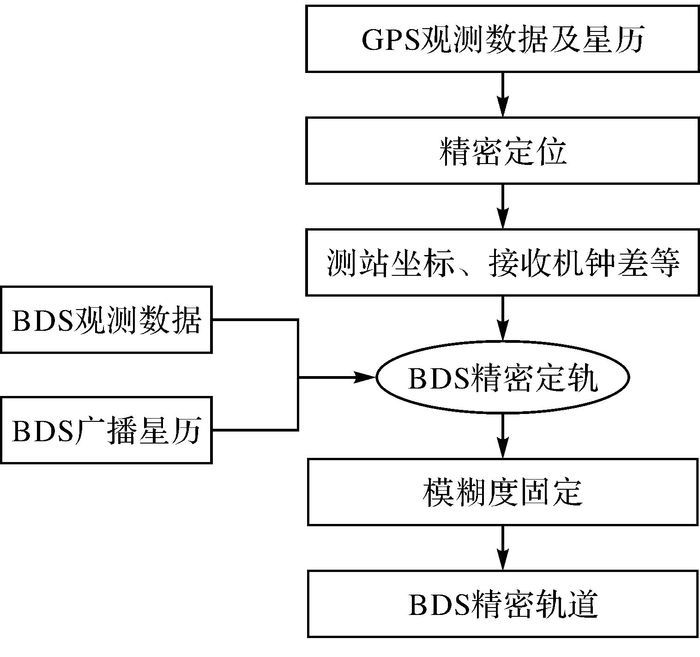
1 原理与方法北斗卫星分为3种轨道,分别为GEO卫星轨道、IGSO卫星轨道和MEO卫星轨道。它们精密轨道的确定基本采用两种方法:一种是直接采用北斗数据计算北斗精密卫星轨道参数;另一种就是采用多源融合技术,利用多模接收机同时接受来自北斗、GPS和GLONASS等卫星的观测数据来提高北斗卫星轨道的精度。由于目前北斗的全球组网还没有完成,而且在全球布设北斗站也存在着很大挑战,导致北斗观测站分布的不均匀,因此仅仅考虑单一的BDS系统得出来的北斗卫星系统的精密轨道精度必然会受限。因此,本文采用第二种方法来计算北斗的精密轨道,首先利用GPS等的观测数据进行精密单点定位,确定测站坐标、接收机钟差、对流层等参数,并将这些参数作为已知值,同时加入北斗的原始的观测值进行北斗卫星的精密定轨。流程如图 1所示。
|
| 图 1 BDS卫星定轨流程 |
导航卫星在轨受到各种摄动力的影响,要想确定卫星的精密轨道必须建立真实的状态运动方程。卫星的运动方程一般是由一组待定的动力学参数来描述的。
假设卫星的状态向量为X, 包含卫星的6轨道参数、一些力学模型参数(各种摄动力参数)和卫星钟差等。X为n维待求参数向量,则它满足的方程为
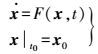 (1)
(1) 式中,x0是卫星的初始状态,在卫星的导航星历中可以获得;F (x, t)为参数有关时间的函数。
用Y记作地面观测量,历元i时刻的观测量yi与观测量的真值G (Xi, ti)之间的误差εi表示为
 (2)
(2) 将式(2) 线性化并取出一阶项
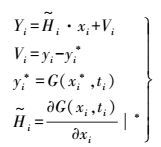 (3)
(3) 式中,xi*为卫星在i时刻的参考轨道,可通过变分方程得到;yi*是由xi*计算得到的几何观测量;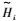
由式(1) 和式(3),可将历元i时刻的观测方程转化为相对于轨道初始时刻t0的观测方程。
 (4)
(4) 多历元的矩阵形式即为
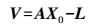 (5)
(5) 式中,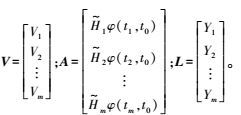
北斗卫星精密定轨问题可以转化为卫星轨道的一个初始状态参数估计问题。利用观测值和已知的初始状态x0,计算卫星轨道参数和力学模型参数的改正值。
3 试验分析本文主要选取全国均匀分布的能够接收四系统数据的国家基准站和全球均匀分布的IGS跟踪网以及MGEX站。所有的测站总共135个,其中国家基准站有32个,它们均能接收到GPS数据;其中58个测站可以接收到北斗数据。IGS测站的初始坐标均从IGS发布的sinex文件中提取出来的,估计时这些坐标约束至亚毫米级;国家基准站的坐标是通过GAMIT计算的周解得数据,相应的约束放到厘米级。
为了分析国家基准站对北斗卫星精密定轨精度的影响,本文采用如表 1的策略设计了两个试验方案。采用的数据是2016年6月28日(年积日为180) 至7月4日(年积日为186) 共7天的观测数据。分别计算单日解和3天解,对计算得出的结果与GFZ发布的当天精密轨道进行比较,判断其外符合精度;用相邻两个3天解比较其重复弧段的精度,判断其内符合精度。
| 类别 | 模型和参数 |
| 观测量 | 消电离层组合伪距和相位非差观测值 |
| 采样间隔 | 300 s |
| 高度截止角 | 7° |
| 时间系统 | GPS时 |
| 模糊度 | 浮点解 |
| 相对论效应 | 考虑 |
| 大气延迟 | 只考虑湿延迟,干延迟不考虑 |
| 太阳光压 | BERN5参数模型 |
| 地球重力场模型 | EGM96模型 |
| 潮汐 | 固体潮、海潮和极潮 |
| 地面接收机相位改正 | igs_absolute_08.atx |
| 初始轨道 | 北斗卫星广播星历 |
| 轨道动力学参数 | 6个轨道卫星状态参数 |
| 卫星和接收机钟差 | 非差消除 |
方案1:只选取IGS站和MGEX站的进行精密轨道计算。
方案2:选取IGS站、MGEX站和国家基准站对BDS卫星进行精密定轨。
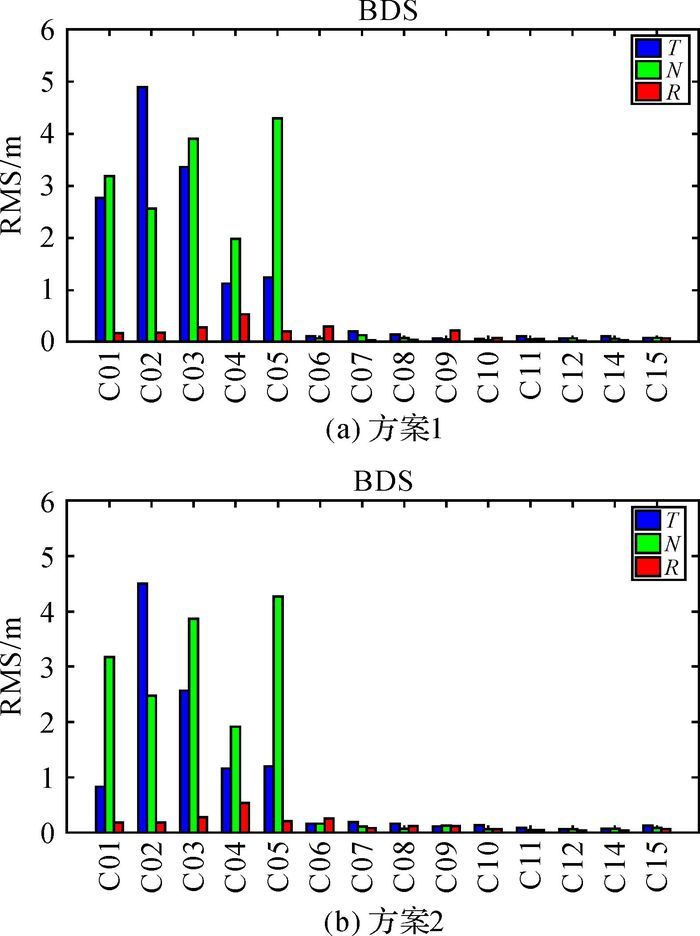
3.1 外符合精度轨道误差表现一般采用的是径向(R)、切向(T)和法向(N)3个方向的误差分量进行描述。首先选取单天的数据计算得到的精密轨道进行比较分析,看一天之内北斗卫星精密轨道精度在切向、径向和法向3个方向的RMS的变化。下面以2016年7月2日(年积日184天)全天的数据解算结果为例,计算得到的结果与GFZ发布的北斗的精度比较结果见表 2和图 2。其中方案1为不加国家基准站的计算结果,方案2为加上国家基准站的计算结果,与设计方案保持一致。
| cm | ||||||||||||
| 类型 | 卫星号 | 切向(T) | 法向(N) | 径向(R) | RMS | |||||||
| 方案1 | 方案2 | 方案1 | 方案2 | 方案1 | 方案2 | 方案1 | 方案2 | |||||
| GEO | C01 | 275.3 | 81.5 | 318.7 | 316.3 | 15.7 | 17.5 | 243.3 | 188.8 | |||
| C02 | 488.5 | 447.7 | 255.5 | 246.6 | 16.7 | 17.4 | 318.4 | 295.2 | ||||
| C03 | 334.9 | 255.5 | 389.8 | 385.6 | 26.9 | 27.5 | 297.1 | 267.5 | ||||
| C04 | 112 | 115 | 196.7 | 191 | 53.3 | 52.7 | 134.2 | 133.2 | ||||
| C05 | 122.6 | 119.2 | 428.5 | 425.5 | 19.3 | 19.9 | 257.6 | 255.4 | ||||
| IGSO | C06 | 9.8 | 15.4 | 2.4 | 14.6 | 28.7 | 24.5 | 17.9 | 18.7 | |||
| C07 | 19.3 | 18.4 | 12.7 | 9.7 | 2.6 | 7.9 | 13.4 | 12.9 | ||||
| C08 | 13 | 14.8 | 7.1 | 6.2 | 4.7 | 11.3 | 9 | 11.4 | ||||
| C09 | 6.4 | 9.6 | 4.4 | 11.7 | 21.4 | 10.9 | 13.2 | 10.8 | ||||
| C10 | 5.9 | 12.4 | 1.9 | 6 | 7 | 4.7 | 5.3 | 8.4 | ||||
| MEO | C11 | 9.3 | 7.4 | 4.4 | 3 | 5.2 | 3.8 | 6.7 | 5.1 | |||
| C12 | 7.5 | 6.5 | 6.5 | 4.7 | 1.6 | 2.7 | 5.8 | 4.9 | ||||
| C14 | 9.9 | 6.4 | 5.3 | 6 | 2.4 | 3.3 | 6.6 | 5.4 | ||||
| C15 | 8.3 | 12 | 7.5 | 7 | 7.1 | 5 | 7.6 | 8.6 | ||||
|
| 图 2 定轨精度 |
由表 2和图 2可以看出,北斗导航卫星3种不同轨道类型的卫星之间的定轨精度差异比较大,总体表现为,MEO卫星定轨精度最好,大约在厘米级,3个方向的RMS值基本都在10 cm以内,径向精度最高,RMS值在5 cm以内。IGSO卫星同MEO卫星的定轨精度在一个量级上,它的RMS值优于20 cm。GEO卫星精度明显比MEO和IGSO的要差,RMS值基本都在米级。这是由于GEO卫星是地球静止轨道卫星,它的静地性使得地面观测几何形状几乎不变,卫星相对于地面的动力学约束信息较弱,使得卫星钟差与轨道误差难以分离。而且GEO卫星的一个特点就是要频繁地机动才能保持与地球静止,难以建立这种推动力的复杂的力学模型,这使得定轨的难度大大增加。增加地面观测值,可使接收北斗数据的测站在全球均匀分布,可以在一定程度提高定轨的精度。相对来说,精度最高的MEO卫星,它的特点是卫星的轨道较高,覆盖范围比较广,受大气阻力的影响可以基本不用考虑,轨道比较稳定,在全球的上空运行,动力学模型相对来说比较好估计,定轨精度比较高。由表 2数据可以看出,北斗卫星精密定轨的轨道精度在径向方向上明显优于其他两个方向,这是由于卫星在轨运行的状态符合开普勒定律,卫星运行的轨迹近似椭圆形,在卫星运行周期能够精确测定的前提下可以较高精度估计出卫星运行轨迹的长半轴,也就是卫星的高度方向(即径向)。
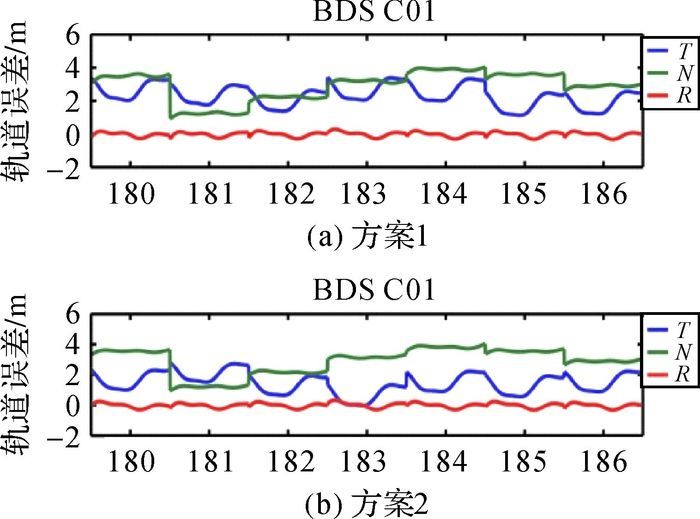
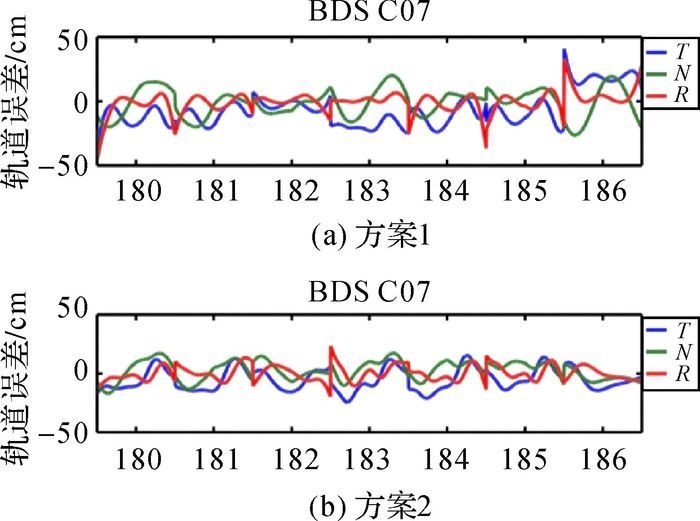
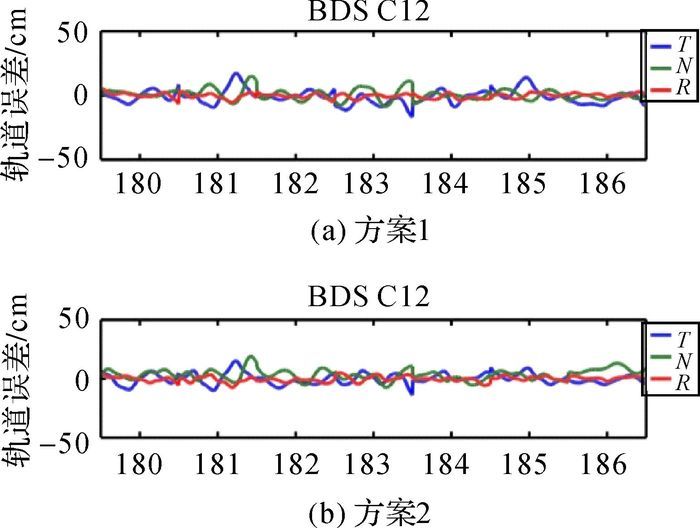
方案1和方案2计算的IGSO和MEO卫星的RMS精度都优于20 cm,其中大部分MEO卫星的RMS值基本都在10 cm左右,两种方案的精度基本相当。MEO卫星在方案1计算的RMS优于10 cm,基本在7 cm左右,方案2加上国家基准站后计算得到的RMS基本在5 cm左右,精度大约提高了20%左右。说明加上国家基准站对中轨卫星在一定程度上会有提高。对于倾斜轨道卫星的定轨精度改善没有那么明显。GEO卫星总体精度得到很大的改善,特别是在切线方向上得到了很大的提高,说明国家基准站的建立对BDS高轨卫星的切线方向的变化监测比较敏感。为了进一步分析两种策略的不同效果,限于篇幅每种类型卫星选取一颗卫星(C01、C07和C12) 并绘制其在3个方向的RMS值在多天的变化情况(如图 3—图 5所示),其他卫星与此情况类似(横坐标为年积日,纵坐标为RMS值)。
|
| 图 3 C01卫星 |
|
| 图 4 C07卫星 |
|
| 图 5 C12卫星 |
从总体来看,北斗卫星精密定轨的精度在不同类型卫星之间有较大差异,与表 2的分析结果一致。每种类型的误差基本均稳定在一定得范围之内。可以看出,对于GEO卫星(以C01为例),方案2比方案1在切线方向上得到明显的提高,平均提高了约0.9 m,在其他方向上提高并不明显。高轨卫星的径向精度也能达到很高的精度,大约在20 cm左右。切向方向上C01到C05的RMS的平均值,在方案1的方法下大约是2.6 m,方案2的均值是2.0 m。可以看出,方案2比方案1在切向上提高了约30%,三维方向上的RMS值提高了36%。这是由于GEO卫星主要是在亚太区域,没有国家基准站之前能够接收北斗数据的MGEX站大多数在欧洲地区,在加上国家基准站以后,GEO卫星的星下点在亚洲地区较少的现状得到改善,能够接收GEO北斗数据的测站明显增多,几何构型得到改善,这些测站对卫星在切向方向上的变化更加敏感,使得高轨卫星的精度有了较大的提高。对于MEO和IGSO卫星在3个方向上没有较大变化,对于IGSO卫星可以看出在方案2下稳定性变得更好,精度有一定的提高。从各个方向曲线变化的趋势来看,RMS值有明显的周期性。它们的周期与卫星在轨运行的周期基本是一致的。GEO和IGSO卫星在3个方向RMS的周期性大约是24小时左右,MEO卫星是12小时左右。
3.2 内符合精度以上的比较只能反映轨道的外符合精度,由于GFZ发布的轨道是利用有限的MGEX计算得出来的精密轨道。MGEX站主要分布在欧洲地区, 且站点分布不合理,特别是对于GEO卫星可视点较少,因此对于高轨卫星的精度对比差别较大。下面以3 d为一弧段对北斗卫星进行精密定轨,得到年积日为184 d的轨道重复弧段的结果(见表 3)。
| cm | ||||||||||||
| 类型 | 卫星号 | 切向(T) | 法向(N) | 径向(R) | RMS | |||||||
| 方案1 | 方案2 | 方案1 | 方案2 | 方案1 | 方案2 | 方案1 | 方案2 | |||||
| GEO | C01 | 93.5 | 56.3 | 27.2 | 26.5 | 3.7 | 3.5 | 56.6 | 36.9 | |||
| C02 | 124.8 | 97.7 | 23.6 | 21.2 | 1.9 | 2.1 | 73.9 | 57.1 | ||||
| C03 | 146.7 | 141.4 | 24.9 | 25.7 | 2.5 | 1.2 | 85.8 | 82.7 | ||||
| C04 | 47.4 | 23.3 | 24.6 | 25.3 | 8.9 | 8.4 | 31.8 | 20.4 | ||||
| C05 | 115.3 | 106.6 | 17.7 | 22.2 | 9.4 | 6.1 | 67.6 | 58.3 | ||||
| IGSO | C06 | 8.1 | 5.5 | 3.6 | 2.1 | 3.9 | 2.8 | 5.6 | 3.8 | |||
| C07 | 18.7 | 16.5 | 5.8 | 2.7 | 3.1 | 2.7 | 11.4 | 9.8 | ||||
| C08 | 13 | 2.2 | 5.4 | 1.8 | 1.2 | 1.3 | 8.1 | 1.8 | ||||
| C09 | 10.3 | 8 | 5.7 | 2.7 | 5.2 | 4.7 | 7.5 | 5.6 | ||||
| C10 | 18.8 | 21.7 | 7.7 | 4.8 | 4.5 | 3.8 | 12 | 13 | ||||
| MEO | C11 | 7.9 | 5.8 | 3.3 | 2.3 | 3.1 | 2.8 | 5.3 | 3.9 | |||
| C12 | 11.8 | 9.5 | 2.7 | 3.3 | 4.4 | 4.1 | 7.4 | 6.2 | ||||
| C14 | 8.4 | 8.2 | 7.2 | 7.9 | 3.9 | 3.5 | 6.8 | 6.9 | ||||
| C15 | 32.2 | 25.9 | 8.4 | 5.2 | 10.1 | 10.2 | 20.1 | 16.3 | ||||
表 3给出了BDS卫星在径向、切向和法向3个方向上的RMS的均值情况。可以明显看出,轨道重复弧段的精度在三类卫星之间也是有较大差异的,与单天解的轨道的RMS值的变化基本是一致的。GEO卫星定轨精度最差,IGSO和MEO卫星定轨精度明显比GEO卫星要高很多。总体表现也是径向精度最好,法向次之,切向最差。在加上国家基准站之前,GEO卫星的RMS值在70 cm左右,也有个别好的卫星,如C04号卫星能达到30 cm。GEO卫星在加上国家基准站之后RMS值优于60 cm,大约提高了17%。在有国家基准站时,IGSO卫星在3个方向的RMS值基本均在10 cm以下,平均RMS是6.8 cm,没加国家基准站时是8.9 cm,精度有了一定的提高。MEO卫星方案2也比方案1一维RMS大约提高了15%。IGS和MEO卫星在径向的定轨精度能达到4 cm的精度。对于GEO卫星的切向精度在加上国家基准站之前平均RMS为1.05 m,加上国家基准站之后为0.85 m,大约提高了24%,可以看出国家基准站对于高轨卫星的切向方向提高显著。可以看出在加上国家基准站之后3种类型的卫星3 d解的内符合精度在一定程度均有了很大的提高。国家基准站对轨道精度的提高有着重要的作用。
|
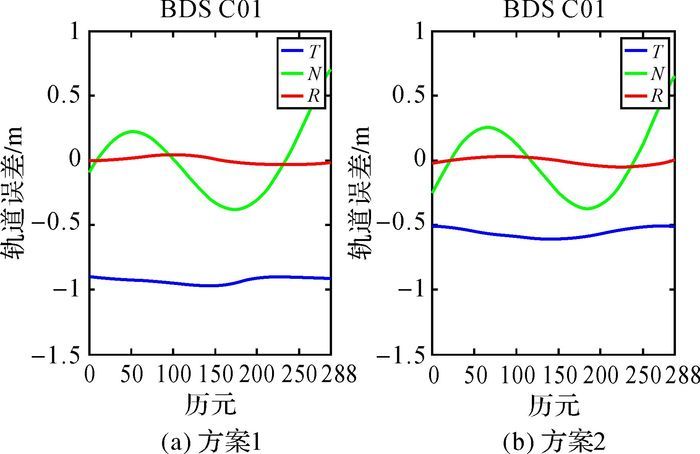
| 图 6 C01卫星 |
|
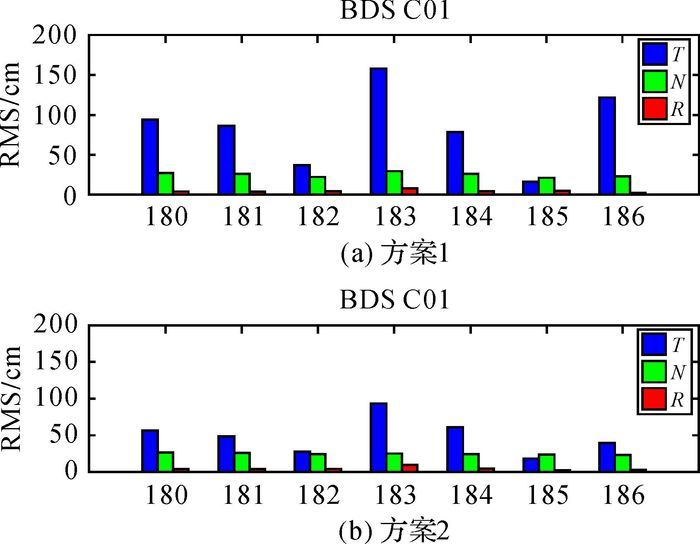
| 图 7 C01卫星 |
从图 6—图 7可以看出,GEO卫星(以C01为例)在切线方向存在明显的系统差,这种系统差可能是由于卫星的频率、几何构型、未模型化的参数等多方面因素造成的。而且在加上国家基准站之后卫星切向的精度得到明显的改善。这是由于国家基准站的建立使测站的分布变得更加合理,几何构型变好,测站对于切向变化敏感。由曲线图可以得出重复弧段与单天解得出的结论相统一,在法向方向具有明显的周期性,与卫星运行的周期一致。
4 结论国家基准站建设的完成,对于BDS卫星的地面观测站逐渐增多,对提高北斗卫星的定轨精度具有重要的意义。本文采用中国测绘科学研究院自主研发的软件进行了试验分析,得出如下结论:
(1) 加上国家基准站后,将计算的单天解轨道与国际上较为权威的分析中心GFZ结果作比较,GEO切向的平均RMS值能达到2.0 m,一维RMS的平均值达到2.2 m,在无国家基准站时切向的平均RMS值为2.6 m,一维RMS的平均值为2.5 m。加上国家基准站对GEO北斗卫星的切向方向了有了明显的改善,可以提高约30%,一维RMS值大约提高了14%。这两种方案在其他方向的精度差别不是很大,在径向方向都能达到20 cm的精度。卫星在径向和切向具有明显的周期性,与卫星的运行周期一致。可以看出国家基准站对于提高北斗高轨卫星的切向方向精度有很大的作用。
(2) 通过重复弧段判断内符合精度,加上国家站之前GEO卫星在切向的平均RMS值为1.05 m,一维RMS的均值为0.6 m。加上国家基准站之后切向的均值为0.85 m,一维RMS均值为0.5 m。加上国家基准站后GEO卫星的切向和三维的RMS分别提高了23%和20%。国家基准站对于改善GEO切向方向的精度起到很大的作用。在切线方向上,IGSO和MEO有了一定的提高。在径向方向上,3种类型的卫星两种方案都能优于10 cm,IGSO和MEO卫星的径向优于5 cm。
(3) 加上国家基准站后,北斗卫星精密各项指标都有所提升,对提高北斗导航定位服务的能力有很大的作用。随着国家基准站不断的投入使用和BDS全球组网逐渐的完成,北斗卫星导航系统的服务的范围和领域将不断地扩大。
| [1] | 杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1–6. |
| [2] | 罗璠, 李建文, 黄海, 等. BDS广播星历的轨道误差分析[J]. 测绘通报, 2015(2): 70–72. |
| [3] | 刘伟平, 郝金明, 李建文, 等. 一种北斗卫星精密定轨方法[J]. 测绘科学与技术学报, 2013, 30(3): 247–250. |
| [4] | 郭标明, 孟祥广, 李宗华, 等. GLONASS卫星广播星历精度分析[J]. 大地测量与地球动力学, 2011, 31(1): 68–71. |
| [5] | LOU Yidong, LIU Yang, SHI Chuang, et al. Precise Orbit Determination of BeiDou Constellation:Method Comparision[J]. GPS Solution, 2015, 20(2): 259–268. |
| [6] | 杜兰. GEO卫星精密定轨技术研究[D]. 郑州: 信息工程技术大学, 2006: 7-14. http://cdmd.cnki.com.cn/article/cdmd-90008-2007051628.htm |
| [7] | 施闯, 赵齐乐, 李敏, 等. 北斗卫星导航系统的精密定轨与定位研究[J]. 中国科学:地球科学, 2012, 42(6): 854–861. |
| [8] | 李冉, 赵春梅, 郑作亚, 等. 基于全球MGEX数据的北斗导航星座精密轨道确定[J]. 大地测量与地球动力学, 2015, 35(1): 662–665. |
| [9] | 张龙平, 党亚民, 许长辉, 等. 地面测控站分布对北斗卫星精密定轨的影响[J]. 测绘科学, 2015, 40(12): 68–72. |
| [10] | 刘伟平, 郝金明, 李建文, 等. 多GNSS融合的北斗卫星精密定轨[J]. 测绘学报, 2014, 43(11): 1132–1138. |


