2. 河南财经政法大学资源与环境学院, 河南 郑州 450046
2. College of Resource and Environment, Henan University of Economics and Law, Zhengzhou 450046, China
当今城市中越来越多的传感器正在产生各种与人类活动相关的时空位置数据,可以称之为时空大数据[1]。作为分析和利用时空大数据的重要手段,数据聚类分析是地理信息相关学科的重要研究课题[2]。目前在大数据环境下的聚类分析方法虽然已经产生不少研究成果,但要么聚类效率无法适应海量时空数据,要么没有解决时空数据的耦合性、关联性、异质性问题。因此,本文拟研究一种适应大数据环境的交通流大数据聚类分析方法,为数据挖掘研究及相关实际应用提供参考依据。
1 国内外聚类分析研究现状目前国内外的时空聚类方法主要包括:① 基于划分的方法:Bagirov[3]提出的全局K-Means算法,雷小锋[4]提出的K-MeanSCAN算法。② 基于模型的方法:Gaffney[5]的回归混合轨迹聚类模型,Chudova[6]的地理实体时空轨迹漂移聚类方法,Alon[7]的地理实体簇临位转换马尔科夫模型。③ 基于密度的方法:Li[8]的交通热点路线的聚类算法,Birant[9]的ST-DBSCAN时空聚类算法。④ 基于大数据的方法:Bose[11]提出的增量并行数据挖掘方法,Laptev[13]的样本抽样放回方法,Zhao[12]提出的基于边结构相似度的聚类方法等。以上研究成果,或是未适应大数据的广域多源特点,或是使用抽样降维方法减少数据量,降低复杂度[14],仍然无法满足大数据环境下聚类分析的需求。
本文的研究策略是在顾及大数据处理效率的条件下,研究一种分布式增量交通流大数据聚类分析流程(distributed incremental clustering process,DICP),该流程在聚类过程中引入分布和增量机制,在分布节点完成大量聚类运算,最终在中心节点完成聚类结果合并,能在较大程度上提高聚类分析的运算效率。对于交通流聚类算法本身,本文研究了一种改进的时空数据聚类算法(the improved method of spatio-temporal data cluster analysis,IMSTDCA),通过时空数据聚集趋势预分析、聚类算法和聚类结果评价3个步骤,完成时空自回归移动平均模型[15](space-time autoregressive integrated moving average,STARIMA)中一体化时空邻域的构建,实现聚类信息的高效挖掘。
2 聚类分析关键技术研究 2.1 分布式增量交通流大数据聚类分析流程本文研究的DICP聚类分析流程,按照多个连续的时间周期,对网络中分布节点和中心节点中的数据进行增量聚类,经过首次历史全集数据聚类和后期多个周期增量数据聚类阶段,可以在满足运算效率的前提下完成较为准确的聚类分析。
2.1.1 历史全集数据聚类阶段首次聚类是针对所有节点历史数据全集进行聚类分析的阶段。首先对分布节点中的数据进行分块,基于MapReduce中的Map运算完成数据块的中间聚类,再使用Combine运算完成分布节点中间聚类结果合并,传输到中心节点后由Reduce运算完成分布节点聚类结果的合并,实现首次聚类分析。其基本思路是:
(1) 对N个分布节点的数据全集进行切块,分为M个数据块。
(2) 对于每个数据块构建一个Map运算,并利用IMSTDCA聚类算法完成中间聚类运算,生成M个中间聚类结果。
(3) 由Combine运算完成M个中间聚类结果的合并,并传输到中心节点。
(4) 在由中心节点使用Reduce运算完成所有聚类结果的二次合并,计算历史全集数据聚类中心。
(5) 若达到最大迭代次数或聚类结果收敛,则完成聚类;否则,计算下一次迭代的比较参数,从步骤(2) 开始进行下一次迭代。
2.1.2 周期增量数据聚类阶段周期增量阶段是在首次聚类基础上,比较增量数据与已有聚类中心的时空距离,利用分布式的优势完成增量数据的快速并行聚类运算。其基本思想是:
(1) 对N个分布节点周期增量数据集合进行切块,分为ΔM个增量数据块。
(2) 对每个增量数据块构建Map运算,并利用IMSTDCA时空距离度量聚类中心与增量数据的时空距离,将增量数据记录合并到小于规定阈值的时空距离最小的类中。
(3) 在分布节点Combine运算中参照聚类中间结果进行偏离误差计算,得到聚类中心在某个分布节点的局部偏离误差,并传输到中心节点。
(4) 由中心节点的Reduce运算进行结果合并,并计算每个类的全局偏离误差。
(5) 若所有全局偏离误差小于阈值,则完成本次周期聚类;若某个全局偏离误差大于阈值,则解体该类,按照历史全集阶段方法重新对未分类数据和解体数据记录进行聚类运算。
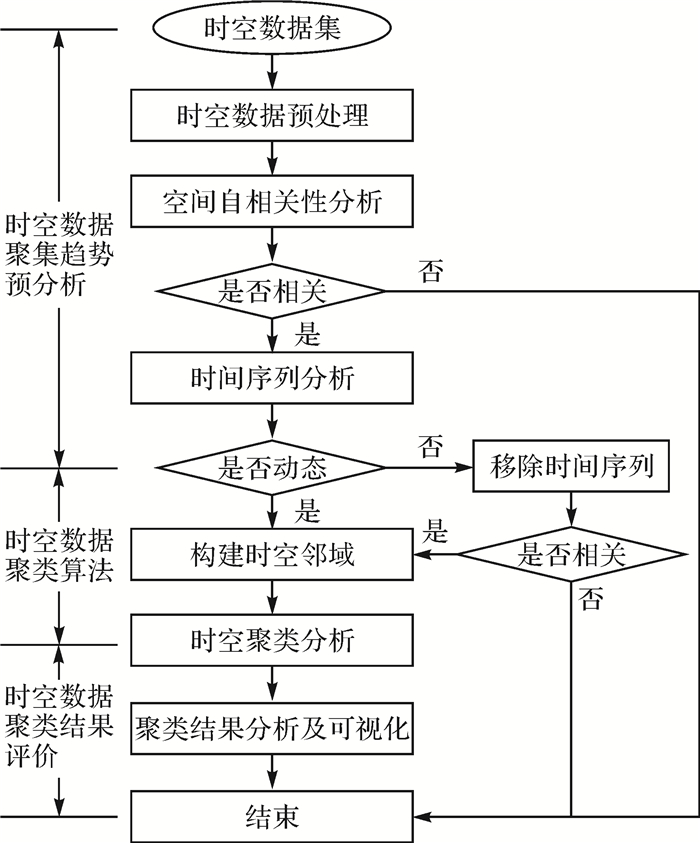
2.2 时空数据聚类算法时空数据聚类分析算法是影响整个聚类分析准确性和高效性的关键因素。本文研究IMSTDCA时空数据聚类分析方法,包括数据聚集趋势预分析、聚类算法和结果评价3个步骤。IMSTDCA聚类分析方法流程如图 1所示。
|
| 图 1 IMSTDCA时空数据聚类分析方法流程 |
时空数据聚集趋势预分析是对数据相关性和异质性进行分析判断,计算地理实体之间是否存在相关性和聚集现象,从而判断进行聚类的可行性,避免大量无谓的聚类分析运算。实际计算中可以利用文献[16]中的Geary’C指数、Moran’I指数、变差函数等方法[16]进行计算,若地理实体空间不相关,则认为其不包含聚集趋势,聚类分析运算没有实际意义。
2.2.2 时空数据聚类算法通过时空数据聚集趋势预分析可以获得时空平稳的数据集合,可以利用经过改进的STARIMA时间延迟算子对数据集的时空邻域进行判断。时空自回归移动平均模型STARIMA公式如下
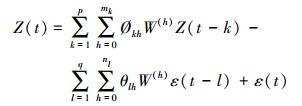 (1)
(1) 式中,k为时间延迟;h为空间间隔;p为时间自回归延迟;mk为第k个时间自回归项的空间间隔;Økh为时间延迟为k并且空间间隔为h的自回归参数;q为移动时间平均延迟;nl为第l个时间移动平均项的空间间隔;θlh为时间延迟为l并且空间间隔为h的移动平均参数;ε(t)为随机误差。式(1) 中的时间延迟k可以代表实体在时间维度的距离,可以通过时空偏相关函数[17]和时空自相关函数[18]计算获得。
在聚类分析过程中,从时间维度分析,前一时间段内的时空实体会对当前时刻的某个时空实体产生影响,而当前时刻的时空实体也会对后一时间段内的时空实体产生影响。因此应该以某一时刻为中心的时间半径作为聚类分析的时间窗口,即将STARIMA模型中的时间延迟k扩展为时间半径。
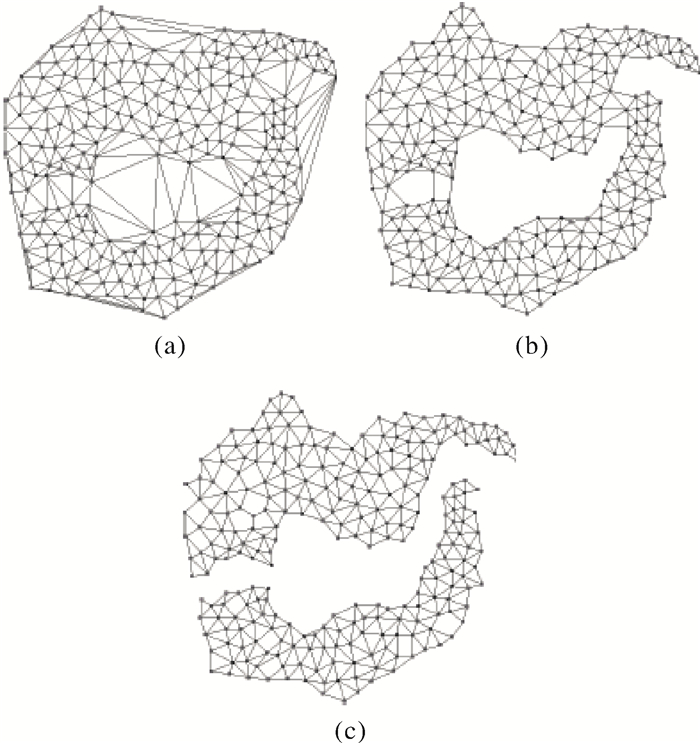
从空间维度分析,要实现实体之间的空间距离定量化计算才能确定聚类分析中的邻近关系。使用Delaunay三角网是判断邻近关系的经典方法,但若三角网未经任何处理,则在边缘部分会产生一定误差,如图 2(a)所示。
|
| 图 2 基于距离约束Delaunay三角网的空间邻近关系 |
本文使用了整体和局部距离约束对空间实体原始Delaunay三角网构建的邻近关系进行修正。针对三角网中顶点Pi的整体距离约束条件公式如下
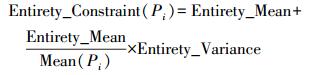 (2)
(2) 式中,Entirety_Mean为所有边长的均值;Mean(Pi)为顶点Pi的所有邻接边的边长均值;Entirety_Variance为所有边长的方差。
针对三角网中顶点Pi的局部距离约束条件公式如下
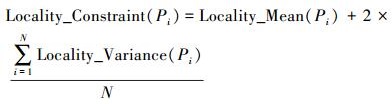 (3)
(3) 式中,Locality_Mean(Pi)为Pi点的邻近边长均值;Locality_Variance(Pi)表为顶点Pi的邻近边长方差;N为三角网所有顶点总数。
利用式(2) 和式(3) 的约束条件边长判断阈值,删除长度大于整体和局部距离约束条件的边,即可得到图 2(b)和(c)中的结果,此时的Delaunay三角网可作为判断空间邻近关系的依据。
通过时间维度和空间维度的邻域分析,即可确定某个地理实体的时空邻域,基于此邻域时空聚类流程如下:
(1) 选取某个实体作为时空中心,判断其时间和空间邻域内的其他实体是否与其满足邻接条件,若满足则标记其为初始时空中心。
(2) 以该初始时空中心为核心,计算邻域内所有实体与中心的时空距离,将距离最近的实体加入聚类簇,第一个聚类集合开始生成。
(3) 重复利用步骤(2) 对聚类集合进行扩展,将每个已加入聚类簇的实体作为扩展中心,在时空邻域中判断实体的时空距离,满足邻接条件即可加入聚类簇,所有满足条件的实体都加入后,即完成了一个聚类集合的生成。
(4) 继续对剩余时空实体重复步骤(1) 至步骤(3) 进行判断,即可生成多个时空实体聚类结合,若某个实体不满足任何邻接条件,则将其标记为孤立点,聚类运算完成。
2.2.3 时空数据聚类结果评价本文中有两个影响时空数据聚类算法复杂度的因素:一是构建时空邻域并在其中检索邻接目标;二是聚类簇的生成。设数据集全中包含n个时空实体,则本文构建时空邻域方法的复杂度约为O(nlog2n),低于ST-DBSCAN[8]方法的复杂度O(n2),而聚类簇簇生成时的复杂度与ST-DBSCAN方法相当。因此本文时空数据聚类算法的复杂度约为O(nlog2n)。
3 试验结果分析试验数据基于智能交通综合管理平台获取,该平台是一套提供了采集评估、交通指挥、智能诱导和联网监控等功能的综合管理平台,目前已经在河南多个地市实现了部分应用。试验提取了系统采集的交通流大数据作为数据源,验证本文设计的分布式增量IMSTDCA时空数据聚类分析方法。
本文对比了3种时空大数据聚类方法:
(1) 局域网集中存储全集时空数据聚类方法(简称LGCP方法)。将分布节点交通流数据抽取,并传输到中心节点,由中心节点对几种存储的数据全集进行Map和Reduce运算,得到聚类结果。
(2) 广域网分布存储全集时空数据聚类方法(简称WGCP方法)。对分布节点本地存储的交通流数据执行Map和Combine运算,在分布节点计算得到中间结果后,传输到中心节点,在中心节点完成结果合并,得到聚类结果。
(3) 广域网分布增量时空数据聚类方法(简称DICP方法)。该方法基于WGCP方法执行,首次聚类完成之后,后续多个时间周期利用增量方式完成聚类,既可保证周期内数据量较为稳定,又可以通过迭代完成聚类结果的优化。
| 数据量 | 抽取时间/min | Map时间/min | Reduce时间/min | 总时间/min | 准确率/(%) |
| 2×107 | 12.32 | 20.52 | 2.53 | 35.37 | 87.91 |
| 4×107 | 23.47 | 48.14 | 5.94 | 77.55 | 89.11 |
| 6×107 | 38.33 | 84.85 | 12.53 | 135.71 | 89.93 |
| 8×107 | 56.41 | 110.93 | 17.05 | 184.39 | 90.62 |
| 10×107 | 69.71 | 144.29 | 24.51 | 238.51 | 91.42 |
| 数据量 | Map时间/min | Combine时间/min | Reduce时间/min | 总时间/min | 准确率/(%) |
| 2×107 | 20.45 | 1.73 | 1.28 | 23.46 | 87.89 |
| 4×107 | 43.62 | 5.31 | 3.32 | 52.25 | 88.83 |
| 6×107 | 65.83 | 8.02 | 5.17 | 79.02 | 89.51 |
| 8×107 | 93.84 | 10.95 | 7.63 | 112.42 | 90.42 |
| 10×107 | 126.39 | 14.77 | 10.05 | 151.21 | 91.36 |
| 数据量 | Map时间/min | Combine时间/min | Reduce时间/min | 总时间/min | 准确率/(%) |
| 2×107 | 20.45 | 1.73 | 1.28 | 23.46 | 87.89 |
| 4×107 | 6.98 | 1.85 | 1.06 | 33.35 | 88.72 |
| 6×107 | 9.34 | 1.95 | 1.23 | 45.87 | 89.42 |
| 8×107 | 18.22 | 2.68 | 1.82 | 68.59 | 90.34 |
| 10×107 | 23.68 | 2.83 | 2.08 | 97.18 | 91.46 |
从聚类效率方面对比3种方法:LGCP方法将数据从分布节点提取到中心节点时,由于数据量大,耗费时间较长,聚类整体效率较低;WGCP方法有效将分布节点计算能力利用起来,但随着系统持续运行,数据全集容量越来越大,聚类时间也会越来越长;DICP方法在首次聚类运算时,参与计算的数据量较小,而后每个时间周期的数据量相对稳定,而且后续周期仅针对增量数据进行运算,可以在较大程度上提高整体计算效率。
从聚类准确率方面对比3种方法,由表 1-表 3的准确率可以看出,数据量对于聚类结果的准确程度起着非常重要的作用,随着数据量的增加,聚类准确率不断提高。因此考虑到聚类准确率,以往的抽样降维方法会导致大量原始数据被筛除,进而影响聚类结果的准确率。而DICP方法采用的分布式增量策略避免了有效数据被筛除,在减小每个时间周期的数据量的基础上,能够保证聚类的准确程度。
从多个时间周期聚类分析得到的集合数量和被解体的集合数量分析,具体见表 4。
| 数据量 | 初始类数 | 结果类数 | 解体类数 |
| 2×107 | 0 | 5 | 0 |
| 4×107 | 5 | 8 | 1 |
| 6×107 | 8 | 12 | 1 |
| 8×107 | 12 | 17 | 2 |
| 10×107 | 17 | 22 | 3 |
从表 4可以看出,新的时间周期都会利用增量数据将原有的一些聚类簇解体,进而生成新的聚类簇,得到更为准确的修正结果。因此,DICP方法更加适合在大数据环境下使用,利用增量解体方式不断修正聚类结果,是保证增量聚类质量的有效手段。
4 结语本文研究了一种基于分布式增量的交通大数据聚类分析方法,并在广域网分布式试验环境中进行了验证。分布式增量聚类流程DICP在分布节点完成大量聚类运算,最终在中心节点完成聚类结果合并,不但可以减少重复计算和迁移拷贝次数,而且可以通过增量机制持续对聚类结果进行修正,能够在保持聚类准确性的条件下提升整体运算效率。其不足之处在于,本文试验数据虽然已经达到一定规模,但分布节点有限,而随着分布节点的增加,中心节点的传输和运算负载会急剧增加,导致计算效率下降,因此为了缓解中心节点压力,可以在今后的试验中设计多层分布式结构,经过分中心的多层聚类,不断合并最终完成全局聚类。
IMSTDCA时空数据聚类方法通过数据聚集趋势预分析、聚类算法和结果评价3个步骤,构建了一体化时空邻域,在考虑时空数据相关性、耦合性与异质性的同时,在时间和空间维度保证了聚类结果的准确性,经过试验证明该方法的聚类结果可靠有效。但本文研究的IMSTDCA聚类方法仅针对交通流时空数据进行了验证,地理实体的时空尺度比较局限,因此在下一步的工作中,还应该对其他类型的地理实体聚类问题进行研究,为预测和决策提供更为有效的数据挖掘方法和工具。
| [1] | 李德仁, 马军, 邵振峰. 论时空大数据及其应用[J]. 卫星应用, 2015(9): 7–11. |
| [2] | 邓敏, 刘启亮, 王佳璆, 等. 时空聚类分析的普适性方法[J]. 中国科学(信息科学), 2012, 42(1): 111–124. |
| [3] | BAGIROV A M. Modified Global K-means Algorithm for Minimum Sum-of-squares Clustering Problems[J]. Pattern Recognition, 2008, 41(10): 3192–3199. DOI:10.1016/j.patcog.2008.04.004 |
| [4] | 雷小锋, 谢昆青, 林帆. 一种基于K-Means局部最优性的高效聚类算法[J]. 软件学报, 2008, 19(7): 1683–1692. |
| [5] | GRAFFNEY S, SMYTH P. Trajectory Clustering with Mixtures of Regression Models[C]//Proceedings of the 5th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York:ACM, 1999:63-72. |
| [6] | CHUDOVA D, GAFFNEY S, MJOLSNESS E, et al. Translation-invariant Mixture Models for Curve Clustering[C]//Proceedings of the 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York:ACM, 2003:79-88. |
| [7] | ALON J, SCLAROFF S, KOLLIOS G, et a1.Discovering Clusters in Motion Time-series Data[C]//Proceedings of the 2003 IEEE Conference on Computer Vision and Pattern Recognition. Los Alamitos, CA:IEEE Computer Society, 2003:375-381. |
| [8] | LI X, HAN J, LEE J G, et al. Traffic Density-based Discovery of Hot Routes in Road Networks[C]//Proceedings of the 10th International Conference on Advances in Spatial and Temporal Databases. Berlin:Springer, 2007:441-459. |
| [9] | BIRANT D, KUT A. ST-DBSCAN:An Algorithm for Clustering Spatial-temporal Data[J]. Data & Knowledge Engineering, 2007, 60(1): 208–221. |
| [10] | ZHENG K, ZHENG Y, YUAN N J, et al. On Discovery of Gathering Patterns from Trajectories[C]//IEEE 29th International Conference on Data Engineering.[S.l.]:IEEE, 2013:242-253. |
| [11] | BOSE J H, ANDRZEJAK A, HOGQVIST M. Beyond Online Aggregation:Parallel and Incremental Data Mining with Online Map-Reduce[C]//Proceedings of Workshop on Massive Data Analytics on the Cloud. New York:ACM, 2010. |
| [12] | LAPTEV N, ZENG K, ZANIOLO C. Very Fast Estimation for Result and Accuracy of Big Data Analysis:The EARL System[C]//Proceedings of ICDE.Piscataway, NJ:IEEE, 2013:1296-1299. |
| [13] | ZHAO W Z, MARTHA V S, XU X W. PSCAN:A Parallel Structural Clustering Algorithm for Big Networks in MapReduce[C]//Proceedings of AINA.Piscataway, NJ:IEEE, 2013:862-869. |
| [14] | 杨杰, 李小平, 陈湉. 基于增量时空轨迹大数据的群体挖掘方法[J]. 计算机研究与发展, 2014, 51: 76–85. DOI:10.7544/issn1000-1239.2014.20130686 |
| [15] | MARTIN R L, OEPPEN J E. The Identification of Regional Forecasting Models Using Space-time Correlation Functions[J]. Transactions of the Institute of British Geographers, 1975, 66: 95–118. |
| [16] | HAINING R P. Spatial Data Analysis:Theory and Practice[M]. Cambridge: Cambridge University Press, 2003: 183-201. |
| [17] | KAMARIANAKIS Y, PRASTACOS P. Space-time Modeling of Traffic Flow[J]. Computers & Geosciences, 2005, 31(2): 119–133. |
| [18] | BEZDEK J C, PAL N R. Some New Indexes of Cluster Validity[J]. IEEE Transactions on Systems Man & Cybernetics Part B, 1998, 28: 301–315. |


